Open Journal of Acoustics
Vol.05 No.02(2015), Article ID:56914,15 pages
10.4236/oja.2015.52004
Implementation of Acoustic Analogies in OpenFOAM for Computation of Sound Fields
J. Schmalz, W. Kowalczyk
Chair of Mechanics and Robotics, University of Duisburg-Essen, Germany
Email: jan.schmalz@uni-due.de, wojciech.kowalczyk@uni-due.de
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 March 2015; accepted 1 June 2015; published 4 June 2015
ABSTRACT
In this work the turbulence based acoustic sources and the corresponding wave propagation of fluctuating flow values in incompressible fluid flows are considered. Lighthill’s and Curle’s acoustic analogies are implemented in the open source computational fluid dynamics framework Open- FOAM. The main objective of this work is to visualize and localize the dominated sound sources and the resulting values of fluctuating pressure values within the computation domain represent- ing the acoustical near field. This is all done on one mesh and during the iterative computation of the transient fluid flow. Finally the flow field and acoustical results of different simulation cases are presented and the properties of the shown method are discussed.
Keywords:
Acoustic Analogies, OpenFOAM, Sound Sources, Sound Propagation, High Performance Computing, Incompressible Flow

1. Introduction
Products like air intake ducts for combustion engines emit acoustic noise mainly based on turbulences and their interaction with solid surfaces. The reduction of these acoustical emissions of technical products and components are becoming increasingly important. In product development process the acoustic parameters are often considered not before an existing mechanical prototype. Usually any changes of concepts, products or components themselves are hardly feasible. Numerical methods like finite elements for structural mechanics or finite volumes for computational fluid dynamics are commonly used by engineers and researchers. Using the advantages of each numerical methods and already existing tools are extended to compute e.g. the sound pressure level in the acoustical far field at a specific observer point. The resulting data is comparable to the results of common acoustic measurements. Concerning the scale disparity between the fluid dynamic pressure and acoustical pressure and the limitation of computation resources often there are used hybrid approaches for computational aero acoustics. Hybrid computational aero acoustic approaches solve the fluid dynamics by e.g. unsteady RANS (Reynolds Averaged Navier Stokes) simulations on a fine mesh in a small domain and then transform the relevant parameters for computing the sound propagation on a coarse mesh representing the acoustical far field.
Further developments in computing methods and parallel communication software and growing resources in computing hardware especially in High Performance Computing (HPC) widen and improve the possibilities to simulate complex acoustic effects. A popular CFD tool is OpenFOAM (Open Field Operation and Manipulation). It is a free, open source software toolbox for Computational Fluid Dynamics (CFD) applications, based on [1] and originally produced by OpenCFD Ltd. It has a lot of various features to solve complex fluid flows in- cluding for example turbulences and chemical reactions up to solid dynamics and electromagnetic and multi physics applications. Almost every feature runs in parallel as standard up to 1000 cores at present and much more in nearer future [2] .
There are different approaches in OpenFOAM for computational acoustics, especially for aero acoustics as mentioned in [3] and approaches based on Linear Euler Equations described in [3] - [5] . These approaches are hybrid approaches and have in common, that they use different meshes to compute the fundamental turbulent fluid flow and acoustic sources on one mesh and the propagation of fluctuating values on another mesh respectively. Nilsson [3] even uses different discretization methods, the finite volume method within the OpenFOAM framework to compute the turbulent fluid flow and acoustic sources and the finite element method to do the sound propagation into the acoustical far field. Stein [4] and Wang [5] do not compute the acoustic sources within the CFD-simulation in particular, they use the Stochastic Noise Generation Method to obtain the source terms and use the Linearized Euler Equations (LEE) to compute the sound propagation. Furthermore the acoustic investigations might be also done during the post processing of the CFD results explained by [6] . In this work the far field solution of the Curle’s Acoustic Analogy is implemented in OpenFOAM. This allows the user to obtain the sound pressure level and its frequency spectrum at a specific observer point only. All mentioned approaches either has in common, that there is a transformation between CFD and CAA (Computational Aero Acoustics) mesh necessary or the acoustic parameter can be determined during post-processing at selective points only.
In this work, the presented approach for computational aero acoustics in OpenFOAM 2.1.1 is mainly based on Curle’s Acoustic Analogy and takes the possibility and availability of high performance computing resources into account. Due to HPC resources, the shown method makes it possible to determine acoustic parameters of flow fields and provides the advantage to compute and visualize the fields of fluid dynamics, acoustic sources and the resulting wave propagation of the fluctuating values of the decomposed pressure (sound propagation) in the acoustical near field and on one mesh only.
2. Theory
2.1. Lighthill’s Acoustic Analogy for Incompressible Fluids
The implementation of acoustic source terms and the corresponding wave propagation of the fluctuating pressure values within the computation domain according to Lighthill [7] - [9] is principally based on the continuity Equation (2.1)
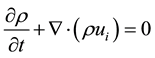 (2.1)
(2.1)
with its density
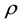 and the velocity
and the velocity
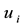 of the fluid. Lighthill’s acoustics analogy is also on the momentum Equation (2.2)
of the fluid. Lighthill’s acoustics analogy is also on the momentum Equation (2.2)
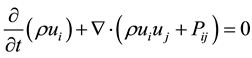 (2.2)
(2.2)
with
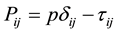 . (2.3)
. (2.3)
In (2.3) the Tensor
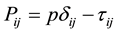 describes the compressive stresses in which
describes the compressive stresses in which
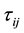 represents the viscous stresses,
represents the viscous stresses,
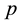 represents the pressure of the fluid and
represents the pressure of the fluid and
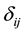 defines the Dirac function. According to [10] the density
defines the Dirac function. According to [10] the density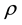 , the pressure
, the pressure
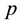 and the velocity
and the velocity
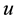 are decomposed into constant and fluctuating parts. The fluctuating parts represent the acoustical values.
are decomposed into constant and fluctuating parts. The fluctuating parts represent the acoustical values.
 (2.4)
(2.4)
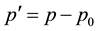 (2.5)
(2.5)
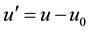 (2.6)
(2.6)
The term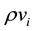 , representing the mass density flux in the continuity equation but the momentum density in the momentum equation. By taking the time derivative on the continuity Equation (2.1) and subtracting the divergence of the momentum Equation (2.2) as documented in [7] and eliminating the term
, representing the mass density flux in the continuity equation but the momentum density in the momentum equation. By taking the time derivative on the continuity Equation (2.1) and subtracting the divergence of the momentum Equation (2.2) as documented in [7] and eliminating the term

if using the decomposed Quantities (2.4)-(2.6). The speed of sound is described by



including the decomposed fluid parameters. Finally the Tensor


and is called the Lighthill-Tensor.
For an incompressible


Following the restrictions for the fluid the density corresponds approximately the density

2.2. Curle’s Acoustic Analogy for Incompressible Fluids
Lighthill’s acoustic analogy was mainly developed for free jet streams. No rigid objects or surfaces are allowed within the computation domain. Unfortunately a large amount of technical application cases need to take into account such surfaces. Curle’s acoustic analogy takes rigid and stationary surfaces and objects within the computation domain into account. It is based on the extended Lighthill Equation [9] (2.11) and represents a special case of the Ffowcs-Williams and Hawkings equation [11] .

The three terms on the right hand side of Equation (2.11) can be interpreted as
Listing 1. Implementaion of Lighthill’s acoustic sources in OpenFOAM, according to [3] .
・ the volume distribution of quadrupoles

・ as surface distribution of monopoles

・ as surface distribution of dipoles

For a rigid object within the computation domain its surface can be described by the auxiliary function

and this yields to an expression which disappears within the volume of the object and becomes one inside the fluid region. As mentioned above this work focuses on the Curle’s Acoustic Analogy, where the considered surfaces are stationary and terms containing velocity components obtain



Additionally for non-porous or rigid control surfaces the following equation is valid:

These assumptions eliminates the surface distribution of monopoles in the extended Lighthill Equation (2.11).
The remaining dipole term


becomes to

if viscous stresses are neglected.


Finally the acoustic source terms of Curle’s Acoustic Analogy are simplified to (2.19)

which are implemented in OpenFOAM acoustic solver according Listing 2.
2.3. Wave Propagation of Fluctuating Pressure Values
Concerning the decomposition of fluid parameters into mean and fluctuating values as described in chapter 2.1 and according the statements in linear acoustics [12] the pressure-density relation can be written as

Listing 2. Acoustic source terms according Curle’s Acoustic Analogy were implemented in OpenFOAM 2.1.1.
where the pressure fluctuations are described by



The wave operator (2.21) with its second time derivative of the fluctuating pressure values is implemented in OpenFOAM as an additional header file shown in Listing 3 where the fluctuating pressure values are defined by the variable pa.
The header files for computation of acoustic sources and for sound pressure propagation respectively are included in the pisoFoam. C-file within the runtime-loop, but after the PSIO (Pressure-Implicit Split-Operator)- loop itself. This provides the computation of the additional acoustic fields during every time step of the pisoFoam-Solver and based on the latest corrected pressure and velocity fields including the computed turbulences of the chosen turbulence model.
The proposed “sound” pressure wave propagation is strongly dependent on the way the computed pressure is decomposed into mean and fluctuating parts. In the presented work the pressure is decomposed into the computed pressure subtracting by the ambient pressure of the initial fluid flow setup. This strongly results in a propagating pressure wave similar to hydrodynamic pressure waves.
Actually there are no specific boundary condition in the OpenFOAM distribution which can perform acoustic behaviors like non-reflecting or absorbing effects neither for incompressible nor for compressible flows. The boundary condition advective works roughly like a non-reflecting boundary condition for incompressible case set-ups. It is based on the OpenFOAM-class mixed FvPatch Field [13] - [16] defining outlet boundary conditions

and its principle behavior is similar to boundary conditions for compressible fluid flow, which is often used for transonic or supersonic simulations. The advective or waveTransmissive boundary condition are applicable on patches defined as outlet only. For a lot of cases these might be insufficient. To overcome this limitation the in this work the computation domain boundary patches are set up as stated in [17] . According to their and Goldsteins [18] proposal the boundary value method is used for several simulation cases. Therefore in inviscid flows the RHS of Equation (2.7) might be set to zero on patches, if the flow velocity on that patches might be neglected.
In Figure 1 the principal program flow of the novel implemented acoustic solver, named acousticFoam for incompressible transient simulations is shown. Before computing the acoustical sources in the acousticSource.H file it is decided due to the case and meshing set up which acoustic analogy has to be chosen for the computation run. Following the wave propagation of the fluctuating pressure values, representing the sound pressure waves within the fluid region are computed by paEqn.H.
Proving the presented principal concept of implementing a computational aero acoustic approach in OpenFOAM several simulations are done and will be presented in the following chapter.
2.4. Acoustic Test Case
For verifying the quality of a numerical solution the results might be compared with the results of the analytical solution of a specific problem, provided that the analytical solution exists. A typical benchmark test case for a novel implemented computational aero acoustic application is the two dimensional acoustic pulse propagation presented by [19] . The advantage of that case is the existing analytical solution obtained from the linearized Euler equations.
Listing 3. Computation of fluctuating pressure wave propagation in OpenFOAM 2.1.1 related to [12] .
2.4.1. Geometric Setting and Meshing
The two dimensional computation domain is a square as showed in Figure 2, where in the center of the domain an initial Gaussian velocity pulse is set up to initiate the wave propagation of the fluctuating pressure values. The domain extends in


Due to the geometric simplicity of the case, the computation domain is meshed by blockMesh, the meshing tool distributed by OpenFOAM. The mesh consists of 40,000 hexahedra elements. The grid spacing of the two dimensional structural mesh is
2.4.2. Numerical Model
On the left hand side of the domain the boundary conditions are set as a velocity inlet, however there is no background flow


Figure 1. Flow chart of OpenFOAM-Acoustic-Solver acous- ticFoam for incompressible simulations.
Figure 2. Set up of acoustic test case.

The two dimensional initial velocity distribution is shown in Figure 3 where the white line marks a cross section which visualizes in Figure 4 the dimensionless initial Gaussian velocity distribution in x- and y-direction. The described initial set up is chosen to compute the transport of the calculated pressure fluctuations based on the acoustic sources. The used application solver was acousticFoam to compute the acoustic sources and the corresponding wave propagation.
The Gaussian distribution for the initial values of the velocity field was set up at the domain center into x- and y-direction to obtain an almost homogeneous initial velocity distribution. If matching both initial fields and analyze and visualize the velocity field values along the cross section line, mentioned above, this results in Figure 4. Hence the peaks of Ux and Uy cannot be equal along this cross section line.
The described initial set up is chosen to compute the transport of the calculated pressure fluctuations based on the acoustic sources. The used application solver was acousticFoam to compute the acoustic sources and the corresponding wave propagation. In this work for all presented incompressible cases air is used as fluid with its kinematic viscosity
Figure 3. Two dimensional initial velocity distribution in x- and y-direction including the cross section line for further investigations.
Figure 4. Initial Gaussian velocity distribution (dimensionless) along the cross section.
The Acoustic Test Case was set to laminar where all the turbulence parameters in OpenFOAM are switched off.
The boundary conditions for the acoustic fields, acousticSources, pSurfaceSources and pa are set each according to Table 1.
To simulate the transient Acoustic Test Case the acousticFoam-Solver based on pisoFOAM-Solver according to chapter 2 is used. The simulation time is set to 0.1 s with a time step of 1.6×10−4 s. The simulation run was done in parallel on 4 processors. The parallel execution time is about 1691 s.
Solving the generated linear equation systems the PCG (Preconditioned Conjugated Gradient)-Solver of OpenFOAM is used for pressure and acoustic fields and the PBiCG (Preconditioned Bi-conjugated Gradient)- Solver for asymmetric matrices like the velocity field or fields relevant for turbulence modelling as turbulent kinetic energy k or specific turbulence dissipation
To compute the wave propagation according chapter 2.3 the second time derivative of the sound pressure field has to be calculated numerically. In OpenFOAM for the second order of time derivative there is the Euler scheme available only.
2.5. Application Case pitzDaily
2.5.1. Geometric Settings and Meshing
The novel implementation of an acoustic solver in OpenFOAM 2.1.1 was tested by running the OpenFOAM distributed tutorial case pitzDaily. This case is a two dimensional set-up of a transient incompressible flow over a backward facing step which is shown in Figure 5 with the corresponding geometrical dimensions given in Table 2.
Figure 5. Set up of OpenFOAM-tutorial case pitzDaily.
Table 1. Settings for the boundary conditions of acoustic fields in Acoustic Test Case.
Table 2. Geometric dimensions of OpenFOAM-tutorial case pitzDaily.
To mesh the computation domain the OpenFOAM-meshing tool blockMesh was chosen. The computation mesh consists of about 12,225 hexahedra elements. This results in an element size of about 0.5 mm concerning the given dimensions in Table 2.
2.5.2. Numerical Model
The physical properties of the fluid are set up as described before in chapter 2.4.2. The velocity u of the fluid flow is set to



To calculate the turbulences the turbulence model kOmegaSST (k-ω-SST) of OpenFOAM is used with the initial values of the turbulent kinetic energy


The setup of the boundary conditions of the acoustic fields like acousticSources, pSurfaceSources and pa is identical to the settings of the Acoustic Test Case above.
The transient pitzDaily―case is computed by the developed application solver acousticFoam with the already mentioned solver settings for linear equation systems. The simulation time is set to 0.1 s with a time step of 1 ×10−6 s. The small geometric dimensions and the relative short simulation time make it possible to run this case in serial on one processor. The serial execution time is about 670 s.
2.6. Application Case Quadratic Brace 2D
2.6.1. Geometric Settings and Meshing
In the quadratic brace 2D simulation case as presented in Figure 6 transient fluid flow around a quadratic brace is simulated. The quadratic brace is positioned in the middle of the domain which is bounded by the inlet and outlet on the left and right hand side respectively and two walls at top and bottom of the domain. The solution of the initial pisoFoam-Simulation represents a virtually steady state solution of a von Kármán vortex sheet behind the obstacle. This solution is used as the initial condition for the aero acoustic simulation with acousticFoam.
The meshing was done with blockMesh. Concerning the dimensions of Table 3 the mesh consists of 2.75 Miohexahedra elements with anelement size of 0.85 mm.
Figure 6. Set up of test case quadratic brace 2 Daccording [20] .
Table 3. Geometric dimensions of test case quadratic brace2D.
2.6.2. Numerical Model
In the quadratic brace 2D simulation case the velocity


Turbulences are calculated by the turbulence model kEpsilon (k-ε) of OpenFOAM with the initial values of the turbulent kinetic energy

In difference to the previous cases the boundary conditions for the acoustic field pa are set according to Table 4.
To simulate the transient quadratic brace 2D―case acousticFoam with the same solver settings for linear equation systems is used as in both other simulation cases before. The simulation time in this case is limited to 0.1 s with a time step of 1 × 10−6 s. The fine mesh granularity and the high time resolution make it necessary to run this case in parallel as well. To reduce the influence of the initial error in acoustic fields the solution of a steady state case is used as initial values for the transient simulation.
3. Results
3.1. Acoustic Test Case
The numerical solution of acousticFoam is compared with the analytical solution (3.1) presented in [19] . The two dimensional numerical results of the Acoustic Test Case computed by the novel developed acousticFoam- Solver are shown in Figure 7. The figure shows the distribution and the propagation of the fluctuating pressure values after to different time steps. Due to the superposed initial velocity distributions the shape of the distribution of fluctuating pressure values is conspicuous and looks like a doubled quadrupole distribution.
The analytical solution of pressure distribution according to (3.1) for a certain time step

is compared with the numerical solution of acousticFoam after certain time step along the cross section line. The shape of the numerical solution fits to the analytical solution curve (Figure 8). There are differences
Figure 7. Two dimensional visualization of propagating pressure fluctuations after two different time steps. White line represents cross section for further investigations.
Table 4. Settings of the boundary conditions for acoustic field pa in quadratic brace2D.
between the numerical and analytical absolute values of the pressure values in the peaks due to the numerical errors of the used linear solvers.
To measure the accuracy of the applied numerical method the error between the simulated solution and the presented analytical solution is calculated. The local error (3.2) at a given time step is the absolute value of the difference between the exact analytical solution and the numerical solution, calculated as following

The Global Error (3.3) is calculated according to the Euclidean norm to

In the presented benchmark test case the global error between the numerical and the analytical solution is computed to 0.38. This global error corresponds to results presented by [21] for compressible two dimensional acoustical wave propagation.
3.2. pitzDaily
The fluid dynamic results of the pitzDaily computation case are well known by OpenFOAM users as a common tutorial case in the OpenFOAM distribution. The first three pictures (a-c) of Figure 9 shows the velocity, pressure and turbulent kinetic energy distribution in the computation domain respectively after 20 ms. Figure 9(d) visualize the distribution of the turbulence based acoustic sources travelling downstream towards the outlet boundary condition.
The results of transient simulation are a snapshot of the developing steady fluid flow over the backward facing step. The developing velocity profile moves downstream towards the outlet and the beginning of the vortex on the ground behind the step is captured in Figure 9(a) and Figure 9(c). The detached vortices next to the trailing edge of the step are the basis for the computed acoustic sources by the application solver acousticFoam. These acoustic source are travelling downstream with the fluid flow. Due to the wall boundary condition at the top of the computation domain there are additional vortices developing over the simulation time.
3.3. Quadratic Brace 2D
The quadratic brace 2D-simulation case was run in parallel on 8 processors. For domain decomposition the scotch method was chosen. The computation domain was decomposed in 8 subdomains according to Figure 10.
The solution of the initial pisoFoam-Simulation according to [20] was used as the initial field for the transient simulation with acousticFoam. The vortex street behind the obstacle is visible in Figure 11 where the fluid dynamic results of quadratic brace 2D are shown.
In Figure 11(b) the stagnation point in front of the obstacle is very good visualized by the pressure distribu- tion within the computation domain. In the other three items of Figure 11 the periodical flow separation is ob- vious. The detached vortices in the flow behind the quadratic brace are well resolved by the kEpsilon turbulence
Figure 8. Wave propagation of fluctuating pressure value after certain time steps; comparison of analytical vs. numerical solution along the cross section line.


Figure 9. Visualization of CFD and CAA results computed by acousticFoam for incompressible flow fields; (a) velocity in x-direction [m∙s−1]; (b) incompressible pressure distribution [m2∙s−2]; (c) turbulent kinetic energy [m2∙s−2] and (d) acoustic sources [kg∙m−3∙s−2].
Figure 10. Quadratic brace 2D domain decomposition for parallel run on 8 processors.
model of OpenFOAM and are represented by the results of the turbulent kinetic energy field and turbulent viscosity field.
In Figure 12 the additionally computed acoustic fields by acousticFoamare shown. The acoustic sources according Curle’s Acoustic Analogy are presented in a different scaling within the same time step to provide a better visualization of the acoustic sources travelling downstream through the computation domain.
The propagation of the fluctuation pressure values in Figure 12(c) do not start from the computed acoustic sources around the obstacle only. There are disturbances recognizable in the acoustic source field and the fluctuating pressure field which start travelling from the outlet patches upstream into the computation domain. This disturbances are caused by numerical errors of the outlet boundary condition which is not perfectly suitable for acoustic simulations.
For investigations of acoustic parameters like “sound pressure”, “sound pressure level” or their frequency spectra a point located at x y (0.06 0) within the computation domainis considered as a specific probe location. This probe location represents a microphone positioned at a distance of 1.5 x (Width D) behind the obstacle along the x-axis. At this probe location the values of the pressure fluctuations are written out every time step of the computation run. During the post processing the time signal of the pressure fluctuations are analyzed by using the GNU Octave library.
The time signal in Figure 13(a) represents the recorded values of the “microphone” at the probe location within the computation domain. The simulated time was set to 0.15 s. The values of the fluctuating pressure decrease with the time of simulation. The high values at the beginning of the simulation are caused by the influ-


Figure 11. Initial field of quadratic brace 2D―test case according to [20] ; (a) velocity in x-direction [m∙s−1]; (b) incompressible pressure distribution [m2∙s−2]; (c) turbulent kinetic energy [m2∙s−2] and (d) turbulent viscosity [m2∙s−1].


Figure 12. Acoustic fields of quadratic brace 2D after 0.5 ms simulated time; (a), (b) acoustic sources [kg∙m−3∙s−2] and (c) pressure fluctuation values [Pa].


Figure 13. Acoustical results of quadratic brace 2D at specific probe location; (a) time signal of “sound pressure” (pressure fluctuations); (b) the time averaged frequency spectra and (c) the filtered “sound pressure level” over time.
ence of the numerical boundary conditions, which are not totally suitable for acoustic simulations. This effect is obvious in Figure 12(c) too. These disturbances at the beginning are smoothed over the simulation time. The original time signal is analysed by applying a Fourier Transformation on it and which results in the frequency spectra shown in Figure 13(b). There are distinctive frequency peaks around 400 Hz, 510 Hz and 800 Hz. These multiple peaks are rather indicators for a tonal sound than for a random noise. The logarithmic measure of the fluctuating pressure values represents the “sound pressure level” relative to the reference value of 20 µPa. Ithas a mean level of about 70 dB which might be a realistic value for the simulated application.
4. Conclusions
The main target of the presented work was to realize acoustic simulations within the open source computational framework OpenFOAM. The Acoustic Analogies according to Lighthill and Curle were implemented in an application solver of OpenFOAM. These modified application solver, called acousticFoam, is developed to compute and solve incompressible fluid dynamic simulation cases regarding turbulence inducted noise. The solver also takes existing walls and objects in the computation domain into account. Using acousticFoam, acoustic sources due to turbulences can be computed and visualized. Based on this computed acoustic sources the propagation of fluctuating values can be also determined and visualized within the “acoustical” near field. The novel implemented method to compute acoustical fields has been verified and validated on the basis of common computational aero acoustical and computational fluid dynamic benchmark cases. The presented work also includes a parallelized computation case. In this simulation case the time signal on a specific measurement point, represented as a probe location within the computed fluid flow is recorded during simulation time. This time signal is used for further acoustic analysis such as frequency analysis or calculating the sound pressure level over time at this specific observer point.
The presented results clarify the principal applicability of the shown method for computing the sound sources of incompressible turbulent flows. The estimation of sound propagation within OpenFOAM is also feasible. The correctness of the presented results are highly sensitive to the used linear solver, chosen mesh granularity and taken simulation time step. The main error concerning the propagation of the fluctuating pressure values occurs mainly because of the second order time derivative in the wave operator on the RHS of Equation (2.10). Up to now there are no boundary conditions concerning any special acoustical behavior like absorbing or non-reflec- tive characteristics in the OpenFOAM distributions implemented yet. Despite to the numerical and methodical limitations similar to [5] OpenFOAM provides, regarding the presented results of the novel developed application solver, the principal ability for computational aero acoustic applications of external flow fields, especially for computing the turbulence based sound sources in the acoustical near field of an incompressible flow field. Due to the disparity of acoustical and fluid dynamic scales which enforces a small time step and a fine granularity of the mesh, the principal approach of implementing acoustic analogies have to take HPC resources into account. Growing and better disposal resources in High Performance Computing and novel HPC applications generate new potentials for computational aero acoustic applications.
Possible applications of the shown method might be the acoustical investigations of air intake systems for combustion engines, HVAC-systems for heating, ventilation and air condition of vehicles or aircrafts, or any other product or system which causes turbulence based acoustic sources. This investigations might be done in an early stage of development process. Hence the results might be used for the optimization of the investigated geometry concerning the aero acoustic emissions and fluid dynamic properties of technical parts or entire systems.
Further development works have to aim at the enhancement of the presented aero acoustic solver in OpenFOAM. One of the most important development steps might be detailed investigations on acoustically suitable boundary conditions with non-reflecting or absorbing characteristics in OpenFOAM. The implementation of the Ffowcs-Williams-Hawkings acoustic analogy will also enlarge the principal applicability of the novel application solver on more realistic simulation cases. Using a compressible application solver as a basis for an improved novel aero acoustic solver will improve it mainly regarding its wave propagation ability. The implementation of acoustic analogies in a compressible application solver of the OpenFOAM-framework will also emphasize the plausibility of the shown method.
Acknowledgements
The authors want to acknowledge the Project “FEToL―Fault Tolerant Framework for peta-scale MPI-Solvers” supported by the German Federal Ministry of Education and Research.
References
- Weller, H.G., Tabor, G., Jasak, H. and Fureby, C. (1998) A Tensorial Approach to Computational Continuum Mechanics Using Object-Oriented Techniques. Computers in Physics, 12, 620-631. http://dx.doi.org/10.1063/1.168744
- Lysenko, D.A., Ertesvåg, I.S. and Rian, K.E. (2012) Modeling of Turbulent Separated Flows Using OpenFOAM. Computers & Fluids, 80, 408-422. http://dx.doi.org/10.1016/j.compfluid.2012.01.015
- Nilsson, J. (2010) Implementation of Acoustical Analogies in OpenFOAM and CALFEM. Lund University. Master- Thesis.
- Stein, A. and Pelz, P.F. (2012) Möglichkeiten und Grenzen numerischer Strömungsakustik mit OpenFOAM, DAGA 2012.
- Wang, Q., Pelz, P.F. and Matyschok, B. (2010) Numerische Simulation von turbulenzbedingtem Schall mit Open- FOAM, TU Darmstadt.
- Kraposhin, M.V. and Strizhak, S.V. (2013) How to Implement Simple Acoustic Analogy in OpenFOAM. 8th Interna- tional OpenFOAM Workshop 2013, Jeju, Korea.
- Lighthill, M.J. (1952) On Sound Generated Aerodynamically I. General Theory. Proceedings of the Royal Society A, 211, 564-587. http://dx.doi.org/10.1098/rspa.1952.0060
- Költzsch, P. (2008) Flow Acoustics. In: Mechel, F.P., Ed., Formulas of Acoustics, 2nd Edition, Springer-Verlag Berlin Heidelberg, 945-1016. http://dx.doi.org/10.1007/978-3-540-76833-3_14
- Curle, N. (1955) The Influence of Solid Boundaries upon Aerodynamic Sound. Proceedings of the Royal Society A, 231, 505-514. http://dx.doi.org/10.1098/rspa.1955.0191
- Ehrenfried, K. (2004) Strömungsakustik: Skript Zur Vorlesung, Mensch & Buch Verlag, Berliner Hochschulskripte.
- Ffowcs Williams, J.E. and Hawkings, D.L. (1969) Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philosophical Transactions of the Royal Society A, 264, 321-342. http://dx.doi.org/10.1098/rsta.1969.0031
- Oshima, T. and Imano, M. (2008) A Full Finite-Volume Time-Domain Approach towards General-Purpose Code Development for Sound Propagation Prediction with Unstructured Mesh. Proceedings of Inter-Noise 2008, Shanghai, 26-29 October 2008, 15 p.
- Poinsot, T.J. and Lelef, S. (1992) Boundary Conditions for Direct Simulations of Compressible Viscous Flows. Journal of Computational Physics, 101, 104-129. http://dx.doi.org/10.1016/0021-9991(92)90046-2
- Colonius, T., Lele, S.K. and Moin, P. (1993) Boundary Conditions for Direct Computation of Aerodynamic Sound Generation, AIAA Journal, 31, 1574-1582. http://dx.doi.org/10.2514/3.11817
- Andreini, Bianchini, Facchin, Giusti, Bellini, Chiti, Grazzini (2011) Large Eddy Simulation for Train Aerodynamic Noise Predictions. Proceedings of the WCRR 2011, Lille, 22-26 May 2011.
- Jangi, M., Tilley, N. and Merci, B. (2009) Numerical Simulations of Some Possible Fire Scenarios in a Closed Car Park with RANS and LES. Proceedings of the IAFSS Advanced Research Workshop, Santander, 15-17 October 2009, 233-242.
- Boersma, B.J. (2004) Numerical Simulation of the Noise Generated by a Low Mach Number, Low Reynolds Number Jet. Fluid Dynamics Research, 35, 425-447. http://dx.doi.org/10.1016/j.fluiddyn.2004.10.003
- Goldstein, M.E. (1976) Aeroacoustics. McGraw-Hill International Book Co., New York.
- Tam, C.K.W. and Webb, J.C. (1993) Dispersion-Relation-Preserving Finite Difference Schemes for Computational Acoustics. Journal of Computational Physics, 107, 262-281. http://dx.doi.org/10.1006/jcph.1993.1142
- Schwarze, R. (2013) CFD-Modellierung-Grundlagen Und Anwendungen Bei Strömungsprozessen. Springer Vieweg, Berlin.
- Tóth, P., Fritzsch, A. and Lohász, M. (2008) Application of Computational Fluid Dynamics Softwares for 2D Acoustical Wave Propagation. Gépészet, 29-30.
Symbols











































