Open Journal of Acoustics
Vol.04 No.03(2014), Article ID:48680,6 pages
10.4236/oja.2014.43010
Peculiarities of Sound Wave in Moving Medium
Vladimir G. Kirtskhalia
Ilia Vekua Sukhumi Institute of Physics and Technology, Tbilisi, Georgia
Email: sipt@siptorg.ge, v.kirtskhalia@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 June 2014; revised 15 July 2014; accepted 11 August 2014
ABSTRACT
Generalized equation for linear gravity waves in moving medium has been obtained. Sound wave is considered as a particular case and it is shown that in inhomogeneous medium at rest it is propagated in full concordance with the Doppler law and principle of motion relativity, i.e. these laws are invariant with reference to properties of medium (homogeneity or inhomogeneity). In moving medium they are fair only in the case of its homogeneity. In strongly inhomogeneous moving medium, propagation of sound is absolutely impossible.
Keywords:
Speed of Sound, Atmosphere, Homogeneous medium, Inhomogeneous medium, Doppler’s effect, Principle of relativity of motion

1. Introduction
As is known, the law of conservation of mass being one of the fundamental laws of physics was formulated for homogeneous medium. However it is still considered universal and up to now has been applied to inhomogeneous medium like the Earth atmosphere [1] -[5] or the ocean [5] - [8] . In recent works [9] [10] it was demonstrated that allowing for the effect of the gravitational field of the Earth this equation needs to be perfected. It resulted in improvement of great number of known gas or hydrodynamic relations as well as to new understanding of the most important properties of medium like compressibility and incompressibility. From here on there has arisen logical necessity of verification of applicability to inhomogeneous medium of fundamental laws of physics like Doppler’s effect and principle of relativity of motion. This theoretical work is dedicated exactly to this problem. In the second section, the equation of linear gravitational wave for moving medium is derived from which dispersive equation for sound wave is obtained as a particular case. Through analysis of this equation in the third section it is shown that if the medium is stationary, the properties of the medium have no influence on sound propagation which occurs in full concordance with the Doppler’s law and the relativity principle of motion. In the case of fixed source and moving medium the properties of medium play a certain role. In homogeneous medium everything remains as before. However in inhomogeneous medium, where the role of isobaric speed of sound is revealed, propagation of sound wave is impossible which can be explained by mechanism of propagation of isobaric sound.
2. Generalized Equation of Linear Gravitational Wave in Inhomogeneous Moving Medium
We deem it expedient to explain to the reader that under the term “gravity wave” we understand mechanical waves generated and propagated in inhomogeneous medium being under the influence of force gravitational field of the Earth. Therefore, these waves have nothing in common with the waves generated as a result of perturbation of gravitational field and can be propagated in vacuum. The equation for linear gravity wave in immovable inhomogeneous medium was first obtained in the paper [9] where it was shown that exactly this equation describes propagation of sound in the Earth atmosphere correctly. Thus, the generally received opinion that the gravitational field does not have any impact on the sound wave was invalidated. In the paper [11] it was shown that application of this equation to the surface gravitational waves is possible only in case of capillary waves and definition of phase speed of common surface gravitational wave, much less the Tsunami wave from the linear theory is incorrect. In this section we will obtain analogous equation for moving inhomogeneous medium.
Let’s consider the generalized system of hydrodynamic equations for inhomogeneous medium in gravitational field of the Earth [9]
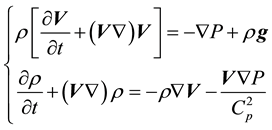 (2.1)
(2.1)
Here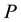 ,
,
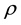 , and
, and
 are pressure, density and speed of fluid, respectively,
are pressure, density and speed of fluid, respectively,
 is isobaric speed of sound.
is isobaric speed of sound.
Assume that the medium is moving with constant speed
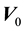 in direction of wave propagation and let’s present all its variables in the form of the sum of their stationary and disturbed values, i.e.
in direction of wave propagation and let’s present all its variables in the form of the sum of their stationary and disturbed values, i.e.
 (2.2)
(2.2)
Then, linearized system of Equations (2.1) will take the form of
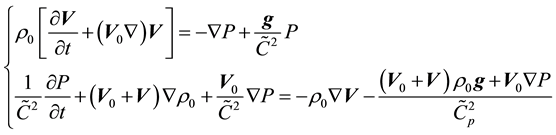 (2.3)
(2.3)
The following equations are used here:
Condition of equilibrium of fluid in gravitational field of the Earth
 (2.4)
(2.4)
The equation of state of the liquid
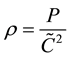 (2.5)
(2.5)
and marks of disturbed values are omitted.
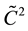 is the generalized meaning of squared velocity of sound towards
is the generalized meaning of squared velocity of sound towards
moving medium , which is reduced from squares of adiabatic
, which is reduced from squares of adiabatic
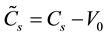 and isobaric
and isobaric
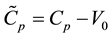 speeds of sound in respect of the moving medium [12]
speeds of sound in respect of the moving medium [12]
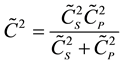 (2.6)
(2.6)
Here
 (2.7)
(2.7)

are relevant speeds of sound in respect of immovable medium characterizing degree of its homogeneity or inhomogeneity [10] .


Let’s apply operator



Having expressed

second one, we will get

From the first equation of the system (2.1) we find that

Substituting (2.11) in (2.10) we obtain

Having taken into consideration that

tion (2.12) due to its obvious smallness, we will finally get

Let’s assume that






Substituting both (2.14) and (2.15) into (2.13), we will obtain the following expression:

Let’s find all variables in the form of plane wave


plitude. Then, we will obtain from (2.16) the following

For




Differentiating Equation (2.19) with respect to


Having substituted (2.18), (2.19) and (2.20) in (2.17) and having ignored the same summand as in (2.12), we will obtain equation for amplitude of linear gravitational wave in moving inhomogeneous medium in the form of

3. Influence of properties of Moving Medium on propagation of Sound Wave
For the sake of simplicity let’s consider sound wave when
(2.21) takes the form of

When


and thus homogeneity (compressibility,

medium at rest have no influence on propagation of sound wave. If medium is immovable and the source of sound is moving towards the receiver with speed of


i.e. frequency shift in any medium occurs according to Doppler’s law [13] . Substitution of


When medium is moving (fixed source and receiver moving with medium) the picture essentially changes. From (3.1) it is clear that in moving inhomogeneous medium frequency shift occurs according to the law different for Doppler’s law.

Equation (3.4) is fair for adiabatic medium representing the troposphere [9] [12] , where speed of the wind is



Equality sign in (3.5) is fair only for strongly inhomogeneous medium, when






As we can see, in weakly inhomogeneous medium frequency shift occurs according to Doppler’s law when the receiver movies in the direction towards the source and the wave length does not change. Substitution in (3.6) of



Thus, for weakly inhomogeneous moving medium






the equation (3.4) results in

While for strongly inhomogeneous media we have

We see that equality of (3.8) and (3.9) describes sound wave only when

For incompressible (strongly inhomogeneous) medium surface integral in (3.10) equals to zero identically, i.e. even when

4. Conclusion
The obtained theoretical results give an evidence that the fundamental laws of physics like frequency shift law of Doppler and the relativity principle of motion are applicable to sound waves in inhomogeneous immovable medium like the Earth atmosphere. Thus it is necessary the sound is to be propagated in horizontal direction. In case of wind these laws are fair up to the height above which in homogeneity effect becomes noticeable. Impossibility of propagation of sound wave in moving inhomogeneous medium proves existence of isobaric mechanism of generation and propagation of sound. Experimental verification of this result will greatly contribute to exploration of the Earth atmosphere as well as to many applied tasks related to air navigation, alpinism and military actions in high-mountain conditions.
Cite this paper
VladimirG. Kirtskhalia, (2014) Peculiarities of Sound Wave in Moving Medium. Open Journal of Acoustics,04,99-104. doi: 10.4236/oja.2014.43010
References
- 1. Gossard, E.E. and Hooke, W.H. (1975) Waves in the Atmosphere. Elsevier, New York.
- 2. Pierse, A.D. (1989) The Wave Theory of Sound. Acoustical Society of America, New York.
- 3. Wang, G.S.K. (1986) Speed of Sound in Standard Air. Journal of the Acoustical Society of America, 79, 1359-1366.
http://dx.doi.org/10.1121/1.393664 - 4. Campos, L.M.B.C. (1983) On Three-Dimensional Acoustic Gravity Waves in Model Non-Isothermal Atmospheres. Wave Motion, 5, 1-14.
http://dx.doi.org/10.1016/0165-2125(83)90002-1 - 5. Landau, L.D. and Lifshitz, E.N. (1988) Theoretikal Physics, Hydrodynamics. 6, Moscow, Nauka.
- 6. Stoker, J.J. (1957) Water Waves. Intersciense Publishers, Inc., New York.
- 7. Lighthill, M.J. (2002) Waves in Fluids. Cambridge University Press, Cambridge.
- 8. Kowalik, Z. (2012) Introduction to Numerical Modeling of Tsunami Waves. Institute of Marine Science University of Alaska, Fairbank.
- 9. Kirtskhalia, V.G. (2012) Sound Wave as a Particular Case of the Gravitational Wave. Open Journal of Acoustic, 2, 115-120. http://dx.doi.org/10.4236/oja.2012.23013
- 10. Kirtskhalia, V.G. (2013) The New Determination of the Criteria of Compressibility and Incompressibility of Medium. Journal of Modern Physics, 4, 1075-1079. http://dx.doi.org/10.4236/jmp.2013.48144
- 11. Kirtskhalia, V.G. (2014) On Gravity Waves on the Surface of Tangential Discontinuity. Applied Physics Research, 6, 109-117. http://dx.doi.org/10.5539/apr.v6n2p109
- 12. Kirtskhalia, V.G. (2012) Speed of Sound in Atmosphere of the Earth. Open Journal of Acoustics, 2, 80-85.
http://dx.doi.org/10.4236/oja.2012.22009 - 13. http://en.wikipedia.org/wiki/Doppler_effect


