Open Journal of Acoustics
Vol.4 No.1(2014), Article ID:43753,12 pages DOI:10.4236/oja.2014.41001
Acoustic Modeling of a 3-Layered Panel Incorporating Electro-Rheological/ Magneto-Rheological (EMR) Fluids
Nader Mohammadi
Department of Mechanical Engineering, Islamic Azad University, Parand Branch, Tehran, Iran
Email: nmohamady@ut.ac.ir
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 8 January 2014; revised 8 February 2014; accepted 15 February 2014
ABSTRACT
Applications of Electro-Rheological (ER) or Magneto-Rheological (MR) fluids as typical smart materials have been widely investigated over the past decades (since their introduction in 40’s). The special applications of these materials as a means of noise suppression are not yet investigated. Constrained Layer Damping (CLD) sheets can be realized by incorporating EMR (ER/MR) materials. In this way, a multilayered damping sheet is obtained with adaptive (tunable) stiffness and damping characteristics. These properties are easily changed in proportion to the electric (magnetic) field applied upon the EMR layer. This notion has been introduced for semi-active vibration control problems. Herein, such panels incorporating EMR material are proposed for adaptive acoustic treatments. Modeling (simulation) of a 3-layered panel with the middle layer being EMR with adjustable properties is carried out in this paper. The tunability of transmission/absorption characteristics of these composite sheets enables us making smart panels for adaptive noise and acoustic treatments. An adaptive performance can be achieved via changing the properties of such panels, on line, according to some sensor outputs. The main objective is to develop proper models to predict the Transmission Loss (TL) of such panels. Also, the TL of this panel is compared with the middle layer of a Newtonian fluid.
Keywords:ER/MR Fluid; Multi-Layers Panel; Transmission Loss

1. Introduction
Recent developments in the technology of smart materials have resulted in the introduction of the EMR (Electro-Rheological/Magneto-Rheological) fluids to make advanced smart structures use composite members filled with EMR fluids.
When an EMR material is subjected to an external field (electric/magnetic field), its acoustical properties and rheological behavior changes. The material resistance to flow increases with increasing electric/magnetic field. This is caused by a significant increase in the viscosity of these materials. EMR fluids can change from a fluid (similar to oil) when no field is applied, to a solid gel almost instantaneously (in few milliseconds) when subjected to a strong electric/magnetic field [1] [2] .
This change is a reversible process. EMR fluids that are solidified under an electric/magnetic field start to flow again by removing those fields or by applying a shear stress, which exceeds a threshold value (yield stress).
Many common fluids (e.g. air, water and liquid metals) behave as Newtonian fluids where shear stress is proportional to shear rate. The ratio of shear stress to rate of deformation (i.e. the shear viscosity coefficient) is virtually constant.
The real behavior of EMR fluids is of course non-Newtonian. The mass and momentum balance equations governing the behavior of Newtonian fluids are the same for non-Newtonian fluids. However, the constitutive equations (stress/strain relationships) are different. The relation between shear stress and rate of deformation is no longer linear.
In this paper, it is assumed that the EMR material obeys the Bingham plastic model. When the field is sufficiently strong, the material stands shear stresses up to a point after which it yields and follows then a Newtonian behavior. Both the yield stress and the viscosity are field dependent [2] .
These properties have led to the design of adjustable or adaptive devices. The traditional ideas of semi-active tunable dampers (shock absorber or engine mount) and EMR clutch is based on the field controlled viscosity [3] [4] . The field controlling solid characteristics has been the basis of notions used in adaptive structures and viscoelastic damping treatments [5] .
A smart/adaptive acoustic panel can also be made by using EMR layers incorporated into the traditional passive multilayered panels. The acoustic properties can then be manipulated according to the required performance in real time simply with the application of proper field. The development of such smart panels supports the design and implementation of modern Active Noise Control (ANC) systems.
Tang et al. [6] experimentally studied the transmission of sound through a triple-layered panel consisting of two plastic plates with an ER mid-layer. The direction of electrical field was parallel to the panel surface so that the wave propagation was perpendicular to the field. Results showed that the effect of electrical field on the SPL (Sound Pressure Level) depends on the plates dimensions. For a plate size of 90 × 90 mm2, SPL increases with the increasing of the electric field. But for a 20 × 20 mm2 plate, the increasing of the field makes the SPL decreases. Hence, the TL values increase accordingly. Wherever, for a plate size of 40 × 40 mm2, the TL values increase with the increasing field at higher frequencies and decrease at lower frequencies. They also investigated the sound transmission through a triple-layered panel made of two flexible electrodes containing a middle layer of ER fluid [7] .
Tang and Lee [8] conducted experiments in which low frequency sound transmission through an ER fluid layer with plastic-aluminum electrodes was investigated. The results showed that, in the 80 - 210 Hz frequency range, the SPL values decrease with increasing the field, while within 210 - 300 Hz, they increase with the electric field.
Recently, Tan [9] presented hybrid compliance-stiffness matrix method for stable analysis of elastic wave propagation in multilayered anisotropic media. He also studied matrix algorithms for modeling acoustic waves in piezoelectric multilayers [10] . Also, he presented recursive asymptotic hybrid matrix method for acoustic waves in multilayered piezoelectric media [11] .
An Attempt is made here to simulate the acoustical performance of a double panel containing EMR liquid. The main objective is to develop proper models to predict the Transmission Loss (TL) of such panels.
Here, wave propagation through the panel is simulated using classical equations governing over layers of solid and liquid media applying appropriate boundary conditions at interfaces.
2. Wave Propagation in Viscous Fluid
The equations for the wave propagation in a continuum are derived combining three fundamental equations: continuity equation(s), equation(s) of motion and state equation(s). We will go through the derivation of these equations for a compressible viscous fluid.
2.1. The Equation of Continuity
Consider flow of a compressible fluid through a small rectangular-parallelepiped element (volume), shown in Figure 1. It is assumed this volume is fixed in space and the fluid flows through it in one-dimension, namely, “ ”. The net mass flow rate through the element surfaces must equal the rate of mass increase within the volume. Hence, continuity leads to
”. The net mass flow rate through the element surfaces must equal the rate of mass increase within the volume. Hence, continuity leads to
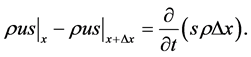 (1)
(1)
In the limit as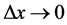 , then
, then
 (2)
(2)
or
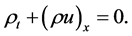 (3)
(3)
2.2. Equation of Motion
The volume is now demonstrated in Figure 1 which is now used to derive the equation of motion. The time rate of the change of linear momentum is equal to the resultant force acting on the body, therefore
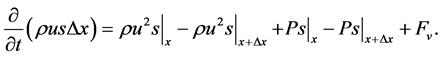 (4)
(4)
In the limit as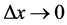 , then
, then
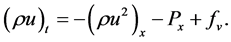 (5)
(5)
Also,
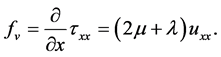 (6)
(6)
From Equations (5) and (6), the one-dimensional form of the equation of motion is obtained.
 (7)
(7)
2.3. The Equation of State
For fluids or gasses the equation of state relates to pressure can be expressed as a function of density and entropy. It is found experimentally that acoustic processes are nearly adiabatic. Under these conditions, the entropy of the fluid remains nearly constant. Then the process is a function of density alone.
For fluids, it is preferable to determine experimentally the relationship between pressure and density. A Taylor’s expansion is written as

Figure 1. The one-dimensional mass flow of a fluid through a small volume.
 (8)
(8)
The coefficients  are determined experimentally or from under analyses. From some derivation coefficient
are determined experimentally or from under analyses. From some derivation coefficient  is equal to
is equal to .
.
Excess pressure or acoustic pressure and excess density is given in form
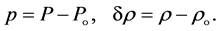 (9)
(9)
From Equations (8) and (9), it can be written in form
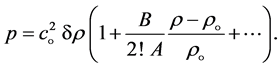 (10)
(10)
2.4. Linearization
The variables associated with sound waves include excess pressure, excess density and particle velocity which may be assumed to be small quantities of first order. First it is assumed
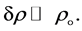 (11)
(11)
From Equations (3) and (9), it can be written as
 (12)
(12)
The second and fourth terms are second-order terms. If the first-order terms are small, then the second-order terms can be neglected. Therefore
 (13)
(13)
Also from Equations (7), (9) and (10) they can be written as
 (14)
(14)
and
 (15)
(15)
2.5. The Wave Equation, Linearized Viscous Case
The linearzed viscous wave equation can be derived combining three equations, (13), (14) and (15). Differentiating Equation (13) with respect to  yields
yields
 (16)
(16)
In the same way, Equations (14) and (15) can be written in the following forms
 (17)
(17)
and
 (18)
(18)
From Equations (16), (17) and (18), the wave equation is obtained as
 (19)
(19)
The shear viscosity coefficient,  , is usually documented for many fluids, but the dilatational viscosity coefficient,
, is usually documented for many fluids, but the dilatational viscosity coefficient, 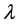 , is not directly measured. Therefore, by Stoke’s condition,
, is not directly measured. Therefore, by Stoke’s condition, 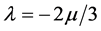 , and Equation (19) is rewritten as
, and Equation (19) is rewritten as
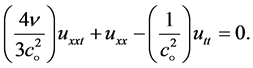 (20)
(20)
2.6. Harmonic Solutions to the Wave Equation
Assume only the wave propagation in positive direction, first. The complex form of the harmonic solution for the particle velocity in Equation (20) is
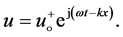 (21)
(21)
From Equation (21), the derivatives are determined:
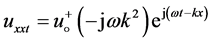 (22)
(22)
and
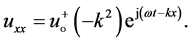 (23)
(23)
Also,
 (24)
(24)
Substitute the above three derivatives into Equation (20). Therefore,
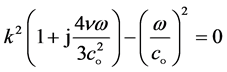 (25)
(25)
or
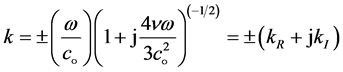 (26)
(26)
where
 (27)
(27)
and
 (28)
(28)
and
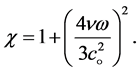 (29)
(29)
From Equations (21) and (26), the wave propagation equation in negative and positive directions is written as
 (30)
(30)
From Equations (17) and (30), the time harmonic solution for the acoustic pressure is determined,
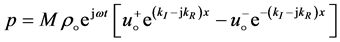 (31)
(31)
or
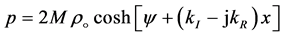 (32)
(32)
where 
3. Specific Acoustic Impedance
The ratio of acoustic pressure to the associated particle speed is defined as the specific acoustic impedance, i.e.
 (33)
(33)
From Equations (30), (31) and (33), the specific acoustic impedance for medium of the viscous fluid is determined. Therefore,
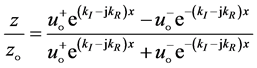 (34)
(34)
where 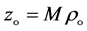 is the characteristic impedance of the viscous fluid.
is the characteristic impedance of the viscous fluid.
Setting 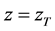 at
at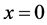 , Equation (34) is written as
, Equation (34) is written as
 (35)
(35)
Assume
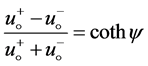 (36)
(36)
or
 (37)
(37)
Therefore,
 (38)
(38)
Now, from Equations (34) and (37), the acoustic impedance can be written as
 (39)
(39)
or
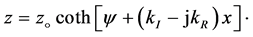 (40)
(40)
For an inviscid (frictionless) fluid, Equation (40) is restated as
 (41)
(41)
4. Infinite Double-Layer Partitions
The panel (structure) to be considered is shown in Figure 2 composed of two impervious layers and the middle filled with viscous fluid (EMR, virtually). In Figure 2, a normal plane wave is assumed incident onto the first layer, passing through and coming out from the right hand side of the second layer. Impedance method is used to derive the ratio of incident pressure to transmitted pressure, and then, the transmission loss of the Interface [12] .
The ratio of incident pressure to pressure on the surface of the left layer is equal to one [13] [14]
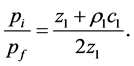 (42)
(42)
Also,
 (43)
(43)
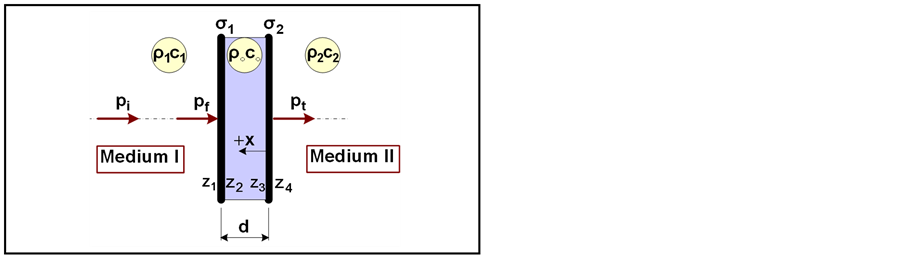
Figure 2. Schematic structure of the double-layer partition.
The layers will be assumed to have no stiffness so that their impedance can be represented by  [14] . Thus, from Equations (42) and (43)
[14] . Thus, from Equations (42) and (43)
 (44)
(44)
Since the wave velocity across the layers is continuous, the ratio of pressures on opposite sides of these layers is equal to the specific acoustic impedance ratio [12] . Therefore,
 (45)
(45)
From Equation (43), the above equation is rewritten as
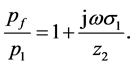 (46)
(46)
From Equations (38) and (40), the specific acoustic impedance of the fluid layer is determined. Hence,
 (47)
(47)
where
 .
.
From Equation (32), the ratio of acoustic pressures at the ends of the middle space is
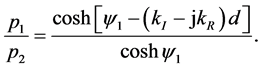 (48)
(48)
The ratio of acoustic pressures on the opposite sides of the second layer is
 (49)
(49)
or
 (50)
(50)
From Equations (44), (46), (48) and (50) the ratio of incident pressure to transmitted pressure is obtained.
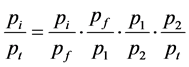 (51)
(51)
or
 (52)
(52)
The Sound Transmission Coefficient (STC) is the fraction of sound power transmitted through a partition. Here,
 (53)
(53)
Transmission loss is a measure of the sound insulation provided by a partition defined as follows
 (54)
(54)
Equivalently,
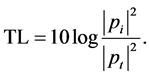 (55)
(55)
The relations stated so far, can now be employed to evaluate the TL of smart double panels incorporating a middle layer of EMR fluid. The effect of applied field appears in the variation of EMR material properties: ,
,  ,
, 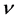 and
and .
.
5. Results and Discussion
For the comparison, the values of transmission loss for typical MR fluid (LORD MRF-241ES) [15] , ER fluid (SILICONE OIL + PNQR polymer particles), water, and air space, at four layer thicknesses is calculated using MAPLE.8. The input data used in the computations is tabulated in Table 1.
The TL values for 1/3 octave band (20 Hz - 20 kHz) is computed and plotted in Figures 3-6. To investigate the effect of field on the TL, the results for the double panel including ER material are also plotted (TL versus field strength, Figure 7)
The following comments can be made based on the results shown in the figures.
The insulation obtained by the air-space is quite good in the frequency range above 1100 Hz. However, using EMR layer with proper thickness (d), a more uniform performance is achieved over the entire frequency range.
Taking an appropriate thickness (d) is of great importance to reach particular design objectives. For instance, d = 0.03 here.
Table1. Input data for calculation of TL of different double panels
. 
Figure 3. The transmission loss (d = 0.01).
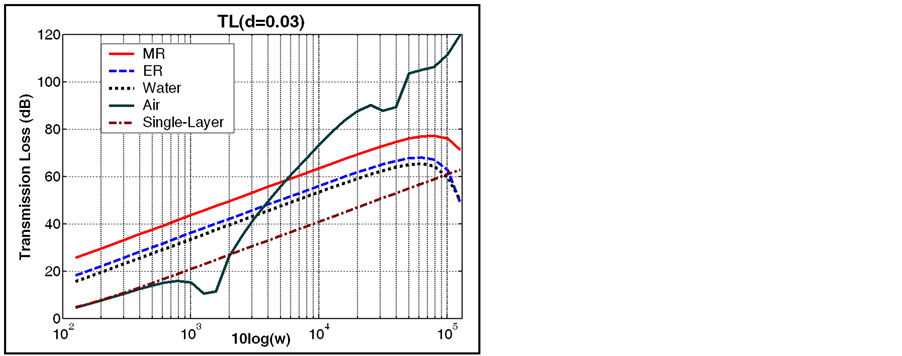
Figure 4. The transmission loss (d = 0.03).
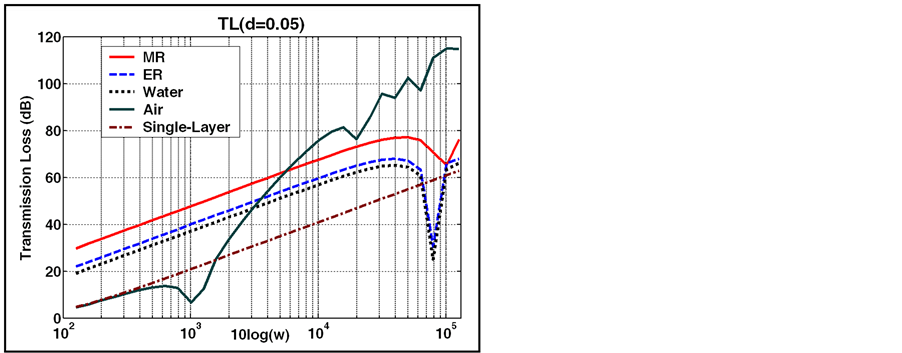
Figure 5. The transmission loss (d = 0.05).
The use of EMR moves the mass-fluid-mass resonance and the cavity-resonance frequencies farther, beyond the audible range. This might be an advantage.
Use of EMR filled panel may also benefit over the low frequency range for which insulation is rather difficult.
The point in any application of such EMR filled panels are their adaptive characteristics. This tunability
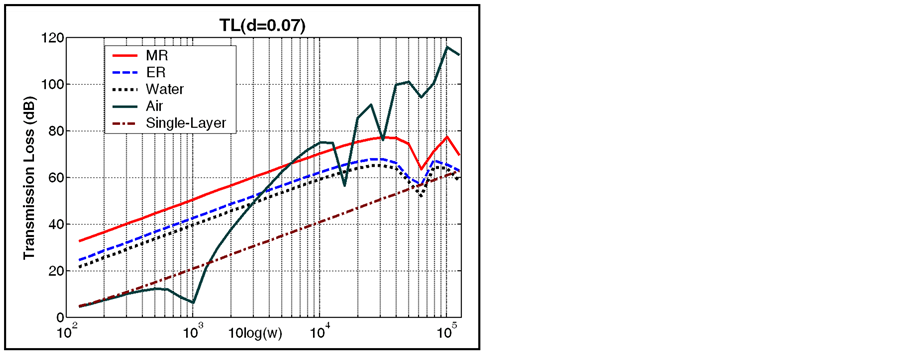
Figure 6. The transmission loss (d = 0.07).

Figure 7. Effect electric field on the TL of a typical ER fluid (d = 0.03).
makes it easy to overcome tradeoffs faced in the design with passive treatments. For the results demonstrated in Figure 7, the panel performance hardly changes below 4 kHz. However, above this frequency the effect of field grows significantly. Further theoretical and experimental investigations are needed to develop this effect more quantitatively.
6. Conclusion
The acoustic performance of double panels filled with EMR fluid as insulators was investigated. The required relations to formulate the transmission loss associated with a multilayered panel were presented. The EMR material was assumed to maintain its liquid state. However, the material viscosity was field dependent and could be adjusted with the application of appropriate electric/magnetic field. Variation of TL versus frequency was computed and compared to common fluids. A typical curve demonstrating the effect of field on the TL of ERF-filled panel was also presented. The results are based on a simplified model of panel filled with Newtonian fluid. More research should be conducted to model ERM/MRM rheology completely and verify the results with further experiments.
References
- Mahjoob, M.J. (1995) On the Identification and Control of Adaptive ER Fluid-Based Structures. Ph.D. Thesis, University of Waterloo, Waterloo.
- Macosko, C.W. (1994) Rheology: Principles, Measurements, and Applications. VCH Publishers, Inc., University of Minnesota, Minneapolis.
- Delivorias, R.P. (2004) Research on Smart Materials: Application of ER and MR Fluid in an Automotive Crash Energy Absorber.
- Yang Jr., G., Spencer, B.F., Carlson, J.D. and Sain, M.K. (2001) Large-Scale MR Dampers: Modeling and Dynamic Performance Considerations. Report. University of Notre Dame, Notre Dame.
- Coulter, J.P. and Duclos, T.G. (1989) Applications of Electroheogical Materials in Vibration Control. 2nd International Conference on ER Fluids, Raleigh, 1989, 300-325.
- Tang, H., Zhao, X. and Luo, C. (2006) Sonic Responses of an Electrorheological Layer with One Side of Grating Electrodes. Journal of Physics D: Applied Physics, 39, 552-557. http://dx.doi.org/10.1088/0022-3727/39/3/020
- Tang, H., Zhao, X. and Luo, C. (2006) Sound Transmission Behavior through a Sandwiched Electrorheological Layer. Fuhe Cailiao Xuebao/Acta Mater Compos Sinica, 23, 128-132.
- Tang, H. and Lee, S.Y. (2007) Direct Experimental Verification of the Sound-Induced Tunable Resonance on a Flexible Electrorheological Layer. Journal of Applied Physics, 101, 131-136. http://dx.doi.org/10.1063/1.2719277
- Tan, E.L. (2006) Hybrid Compliance-Stiffness Matrix Method for Stable Analysis of Elastic Wave Propagation in Multilayered Anisotropic Media. Journal of the Acoustical Society of America, 119, 45-53. http://dx.doi.org/10.1121/1.2139617
- Tan, E.L. (2007) Matrix Algorithms for Modeling Acoustic Waves in Piezoelectric Multilayers. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54, 2016-2023. http://dx.doi.org/10.1109/TUFFC.2007.496
- Tan, E.L. (2011) Recursive Asymptotic Hybrid Matrix Method for Acoustic Waves in Multilayered Piezoelectric Media. Open Journal of Acoustics, 1, 27-33. http://dx.doi.org/10.4236/oja.2011.12004
- Beranek, L.L. and Work, G.A. (1949) Sound Transmission through Multiple Structures Containing Flexible Blankets. Journal of the Acoustical Society of America, 21, 419-428. http://dx.doi.org/10.1121/1.1906530
- London, A. (1949) Transmission of Reverberant Sound through Double Walls. Journal of the Acoustical Society of America, 22, 270-279.
- Fahly, F. (2001) Foundations of Engineering Acoustics. Academic Press, Waltham.
- LORD RheoneticTM (2003) Magnetically Responsive Technology. Product Bulletin, LORD RheoneticTM.
Nomenclature
 : Sound velocity in the viscous fluid;
: Sound velocity in the viscous fluid;
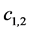 : Sound velocity in the media
: Sound velocity in the media ;
;
 : Distance between two impervious layers;
: Distance between two impervious layers;
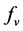 : Viscous force per unit volume;
: Viscous force per unit volume;
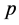 : Acoustic pressure at any point;
: Acoustic pressure at any point;
 : Acoustic pressure at ends of the viscous fluid media;
: Acoustic pressure at ends of the viscous fluid media;
 : Acoustic pressure on the surface of the left hand first layer;
: Acoustic pressure on the surface of the left hand first layer;
 : Incident acoustic pressure;
: Incident acoustic pressure;
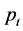 : Transmitted acoustic pressure;
: Transmitted acoustic pressure;
 : Surface that mass flows through it;
: Surface that mass flows through it;
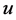 : Particle velocity;
: Particle velocity;
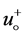 : Amplitude of the particle velocity;
: Amplitude of the particle velocity;
 : Amplitude of the particle velocity;
: Amplitude of the particle velocity;
 : Viscous force;
: Viscous force;
 : Instantaneous pressure at any point;
: Instantaneous pressure at any point;
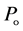 : Static pressure in the viscous fluid;
: Static pressure in the viscous fluid;
 : Transmission loss;
: Transmission loss;
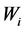 : Incident sound power;
: Incident sound power;
 : Transmitted sound power;
: Transmitted sound power;
 : Specific acoustic impedance;
: Specific acoustic impedance;
 : Dilatation viscosity coefficient;
: Dilatation viscosity coefficient;
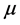 : Shear viscosity coefficient;
: Shear viscosity coefficient;
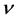 : Kinematics viscosity coefficient;
: Kinematics viscosity coefficient;
 : Instantaneous density at any point;
: Instantaneous density at any point;
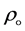 : Static density in the viscous fluid;
: Static density in the viscous fluid;
 : Static density in the media
: Static density in the media ;
;
 : Surface density of the layers
: Surface density of the layers ;
;
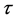 : Sound transmission coefficient;
: Sound transmission coefficient;
 : Component of the viscous stress tensor;
: Component of the viscous stress tensor;
 : Angular frequency.
: Angular frequency.


