Open Journal of Acoustics
Vol.2 No.4(2012), Article ID:25473,4 pages DOI:10.4236/oja.2012.24016
Some Reasons to Revise the International Standard ISO 226:2003: Acoustics—Normal Equal-Loudness-Level Contours
Espoo, Finland
Email: ej.parmanen@gmail.com
Received October 5, 2012; revised November 15, 2012; accepted November 27, 2012
Keywords: Loudness; Loudness-Level; Loudness Function; Phon Definition
ABSTRACT
The recent Standard ISO 226 concerning equal-loudness-level contours has been critically analysed. As a result, it is shown that the fitting and smoothing processes applied in the standard lead to parameter values defining equal-loudness-level contours that are not consistent with the chosen loudness function type. Serious mathematical and acoustical discrepancies have also been found that result in constant terms having an unnecessarily high numerical accuracy and a flawed phon definition, which leads to an erroneous loudness level representation. Therefore an extensive treatment of the logarithmic calculations (phon) of a loudness function is performed in this study. Finally, the author concludes that it would be desirable for the discrepancies in the standard (shown in the study) to be taken into account and corrected before publishing a new version of the standard.
1. Introduction
An international researcher group of Japanese scientists (serving as project leader) and researchers from Germany, Denmark and the United States has produced the recent determination of equal-loudness-level contours for the human auditory perception system called ISO 226:2003 (E): Acoustics—normal equal-loudness-level contours [1].
Particularly because the equal-loudness-level contours in the standard are now based on a chosen loudness function, the equal-loudness-level contour complex is of special interest. Namely, such a function defines the upward and downward behaviour of the contours, providing an unequivocal view of how the subjective loudness grows between the contours. The author [2,3] of this study has earlier derived similar contours based on Stevens’ power law, also mentioned as an alternative loudness function by Suzuki and Takeshima [4].
The derived contours in [2] were almost identical to the equal-loudness-level contours in the former ISO standard ISO 226:1987 [5]. However, no loudness function appears in this standard, although the contours are shown as a result of mathematical expressions. In fact, purely mathematically, there are lots of mathematical expressions that could simulate such contours without any connection between the expression (and its parameters) and the acoustical or psycho-acoustical terms. It proved [2] that the mathematical expressions based on defined acoustical quantities and Stevens’ power law were simpler than the expressions used to achieve similar contours in the standard [5].
In the present study, the derivation of equal-loudnesslevel contours in ISO 226:2003(E) [1] is first reviewed and analysed. The review is fairly critical because the author found several discrepancies which partly (at least) spoil the contour complex system shown in the standard [1]. Problems concerning interpretations of loudness functions and, in particular, loudness levels seem to be somewhat general but also have disturbing effects on the standard [1]. These are treated more extensively in the technical chapters of this study, which is mostly performed by following the excellent informative part (Annex C) in the standard [1].
Finally, the author has some reservations concerning the statistical validity of the data and of applying advanced fitting methods and the fitting in general: For example, the data does not consist of a homogeneous solid sample of normal hearing people. Instead, the scattered measurements and calculations are performed by different researchers and laboratories in different countries and on different continents. Therefore the sources of error are pretty numerous. However, possible problems arising from the non-validities of the data can not be treated in detail here.
2. The Loudness Function
A loudness function (a mathematical model or estimate) represents the subjective strength of the auditory perception of a given sound defined by its magnitude (sound pressure level) and frequency (pure tone or narrow band sound). The international group has applied the following basic loudness function [1], l:
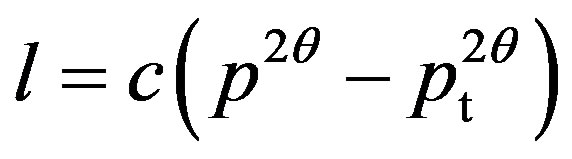 (1)
(1)
where c is a dimensional constant, p is the sound pressure of a pure tone, θ is the exponent of the loudness-perception process and pt is the threshold of hearing in terms of sound pressure [1]. Although this form of describing a loudness function is quite common in the literature, there is a drawback caused by the use of non-dimensionless sound pressure (or square sound pressure). This seems to create troubles with the main equations in the standard [1], as seen later. A more useful form of Equation (1) would be
 (2)
(2)
or
 (2’)
(2’)
where the pressures are written in dimensionless (the loudness function should be dimensionless) magnitudes of sound pressure squares (in sound pressure levels (dB)), and in the latter equation θ is taken to be 1/k. k (the root notation, see e.g. [2,3] by the author) is shown here because it refers to Stevens’ power law stating that the loudness is proportional to a distinct root of the sound intensity. In addition, it should be noted that Equations (1) and (2 and 2’) do not differ provided that the square pressure magnitude is (p/po)2, where po is the reference pressure 20 μPa, in Equation (1). However, this seems not to be the case in [1].
The frequency-dependent exponent θ (or the root k) is the most important and crucial quantity when considering, in particular, loudness and equal-loudness or equal-loudness-level contours according to Equation (1). Very little attention has paid to this fact in [1].
For example, as stated by Suzuki and Takeshima [4], Stevens’ power law takes the form (written here with the same notation as Equation (2))
 (3)
(3)
The author has deduced [2] that if the parameters c and θ are determined for a type of equation like Equation (3), in each frequency band the equal-loudness-(level) contours are wholly determined. Note that θ (having the value of 0.3 at 1000 Hz according to Stevens’ power law) has the same significance at every frequency band, i.e. θ is not important only at 1000 Hz, and that θ varies depending on the frequency band. Consequently, he has derived the contours [2] shown in the former standard ISO 226:1987 [5]. It is worth emphasising that θ wholly determines the growth of the loudness function (3) at each frequency band.
It may seem that Equation (1) is a problematic loudness function because of the vanishing property at the threshold, but this is not the case. In fact, Equation (1) is neither a new nor a different loudness function if compared with Equation (3). Rather, Equations (1) and (3) are wholly the same, with the difference that in Equation (1) the threshold loudness (the loudness function value at the threshold sound pressure level) has been removed to zero. Then, of course, Equations (1) and (2) vanish (take the value of zero) at the threshold. However, this is not a problem because Equation (1) must also be allowed to take negative values.
In fact, Equation (3) and the first part (cp2θ) of Equation (1) are similar basic loudness functions estimating the behaviour of the human auditory perception system in regard to sounds that can be heard. This implies that, if the threshold has been determined e.g. for people with normal hearing, people who have very good hearing (hearing sounds below the general threshold) must also have a loudness function. Equation (1) then takes negative values and does not vanish, and the threshold loudness-level contour may be seen rather as one of the equal-loudness-(level) contours of the whole system. If so, the threshold loudness-level contour should be considered of particular importance, because it is the only contour that is based on a human subjective impression or experience resulting in an exact expression: “The sound cannot be heard”.
Possibly as a consequence of this fact, the least scattered values of the sound pressure levels around the fitted loudness level contours lie at the threshold contour (best fit) in the standard [1]. Upwards the fittings seem to become poorer and poorer.
It now appears that to perform the equal-loudness (-level) contours, it would have been enough for the international group to consider the actual loudness function, i.e. the first part (cp2θ) of Equation (1) only. However, no analysis has apparently been done of the problem that emerged. In continuing to develop type-equation (1) of the loudness function, they state: “there are two different processes in assessing loudness: one is a ‘loudness perception process’; the other is a ‘number assignment process’.” The group finally concludes that a process of assessing loudness rating consists of three parts, includeing a linear transfer function, a loudness perception and a number assignment. On this basis the group finally rewrites Equation (1) as
 (4)
(4)
where p, pt and α (= θ) are as in Equation (1), U is an extended linear transfer function [1], b and β are those for the number assignment process [1], respectively and c is an extended dimensional constant [1]. One may rewrite Equation (4) as
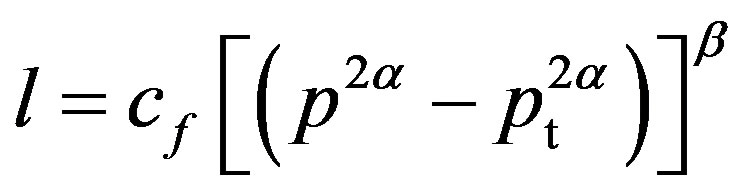 (5)
(5)
where cf is a combined dimensional constant of b, c and U in Equation (4) depending on frequency as c in Equation (1). It is clear that also in Equation (1) c must depend on the frequency. However, both c and cf are (by definition) independent of the pressure (or sound pressure levels). Therefore cf can never have such a value that these equations are the same, i.e. the loudness functions (1) and (4) are surely different (provided that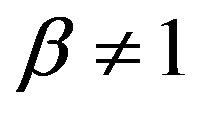 ). It also seems that the desire of the international group to include two or three different processes or parts in a loudness process has been reduced to a foreign exponent β in the “original” loudness function (1).
). It also seems that the desire of the international group to include two or three different processes or parts in a loudness process has been reduced to a foreign exponent β in the “original” loudness function (1).
The group states that “…When the loudness of a 1000-Hz pure tone is equal to the loudness of an f-Hz pure tone, the following equation can be derived from Equation (C.2) (Equation (4) here)”. The “following equation” is
 (6)
(6)
where the subscript “f” refers to frequency band dependence with “r” referring to 1000 Hz. However, one cannot derive this equation from Equation (4) except providing that b = c = β = 1. The group has obtained the frequency-dependent parameters αf (replacing θ in Equation (1)) and  by mathematical fitting and smoothing methods from Equation (6) by defining additionally
by mathematical fitting and smoothing methods from Equation (6) by defining additionally
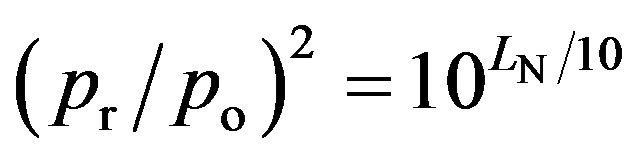
(at 1000 Hz), where LN is the constant loudness level parameter chosen to derive the loudness level contour considered. Equation (6) can be rewritten in the form
 (7)
(7)
One can see that the chosen loudness function (1) with the dimensional constant  (replacing c in Equation (1)) has been set at the same value as the loudness function in the 1000 Hz frequency band. Here, of course, the right-hand side of Equation (7) represents a known loudness function at 1000 Hz with a known dimensional constant (= 1) and the known exponent θ = αr (= 0.250).
(replacing c in Equation (1)) has been set at the same value as the loudness function in the 1000 Hz frequency band. Here, of course, the right-hand side of Equation (7) represents a known loudness function at 1000 Hz with a known dimensional constant (= 1) and the known exponent θ = αr (= 0.250).
However, the chosen loudness function (Equation (1)) requires that in Equation (7) the second term on the left-hand side has the same loudness value as the second term on the right-hand side (the threshold loudness value). Therefore, Equation (7), as does Equation (6), reduces to (here the reference pressures are also shown)
 (8)
(8)
Equation (8) shows that the parameters αf and  in the standard [1] could have been determined from a simpler equation than Equation (6). Namely, a significant advantage of Equation (8) is that that it can be reduced to a linear equation (provided that the sound pressures are shown in decibels). By using the notation in the standard [1] (LU = 10lg
in the standard [1] could have been determined from a simpler equation than Equation (6). Namely, a significant advantage of Equation (8) is that that it can be reduced to a linear equation (provided that the sound pressures are shown in decibels). By using the notation in the standard [1] (LU = 10lg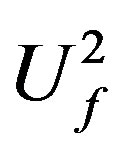 ) and the defining above taking into account the requirement to have for an equal-loudnesslevel contour the same quotation (phon value) as the sound pressure level at the crossing point (at 1000 Hz) at the dB axis, Equation (6) finally becomes
) and the defining above taking into account the requirement to have for an equal-loudnesslevel contour the same quotation (phon value) as the sound pressure level at the crossing point (at 1000 Hz) at the dB axis, Equation (6) finally becomes
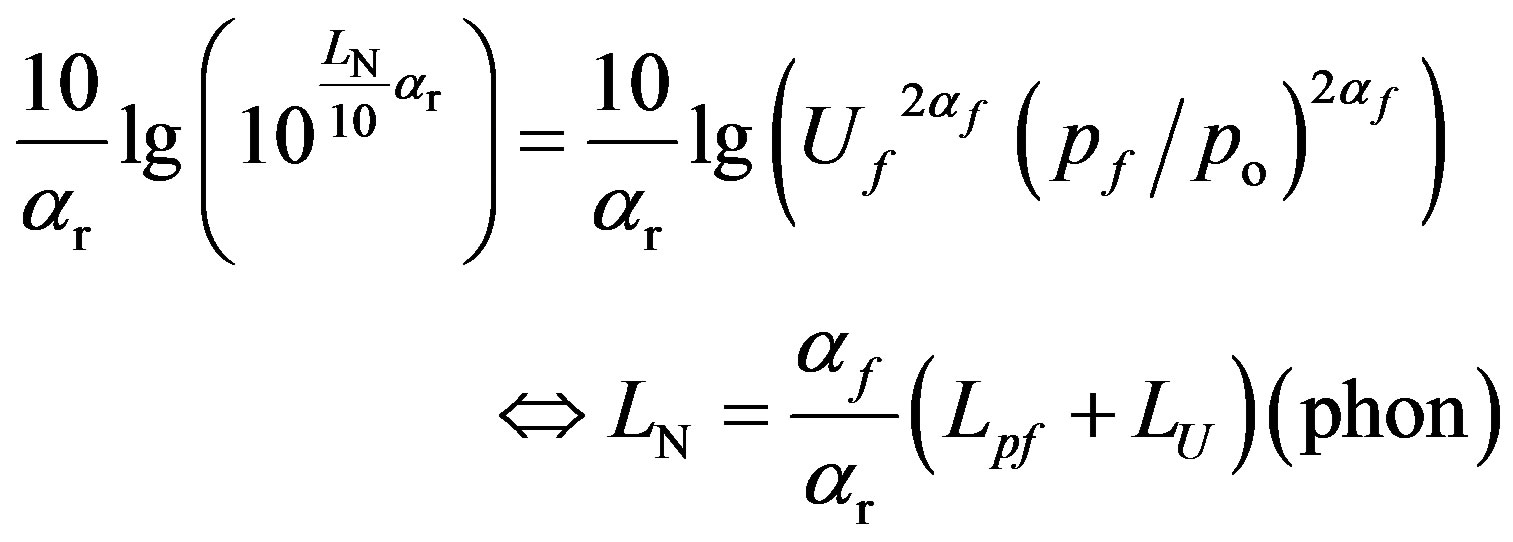 (9)
(9)
including LU as a frequency dependent weighting on the sound pressure level domain [2].
The latter equation, a form of Equation (6) would have helped and simplified the fitting and smoothing processes considerably. Note here that if LU is solved from Equation (9), LU only depends on the frequency (band). Thus, after determining αf, LU is wholly determined independently of the equal-loudness-level contour considered (the threshold contour, for example).
Besides the complicated form of Equation (6), the respective main equations in the standard [1] differ formally from this Equation (6) and are principally different than Equation (9). The equation for Lp is written [1]:
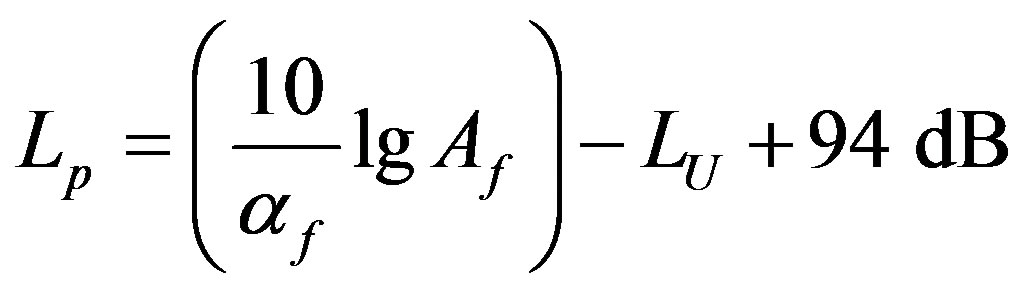 (10)
(10)
where
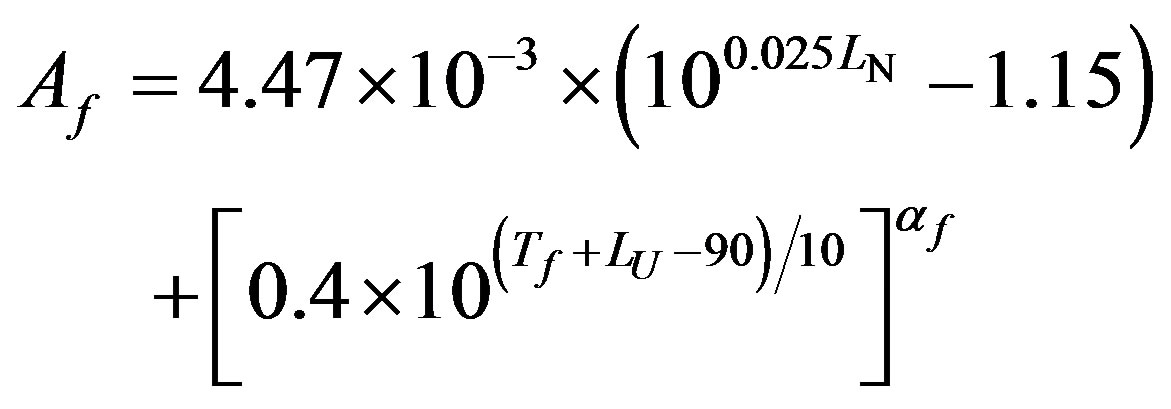
where LU (note that LU here differs from the LU above) is a magnitude of the linear transfer function normalised at 1000 Hz [1] and Tf is the frequency-dependent threshold sound pressure level. The mystic constants having numerical values of 4.47, 1.15, 0.4 and 94 dB are not defined in the standard. Anyhow, if LN is solved from Equation (10) the loudness level according to the standard [1] finally becomes [1]:
 (11)
(11)
where
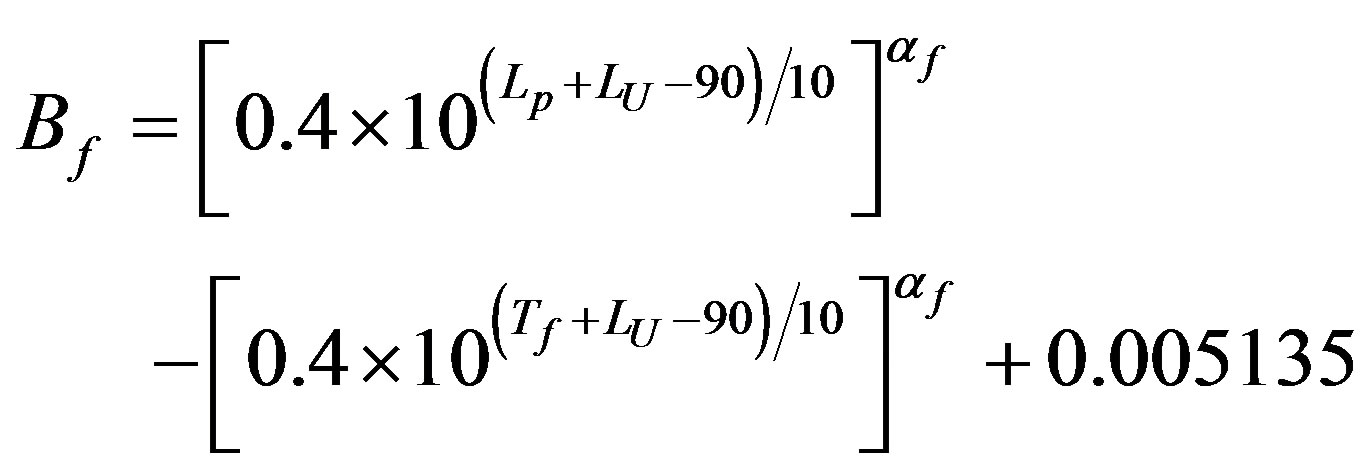
Because of the great accuracy of the last constant term in Equation (11), the author’s reservations first arose here. It seems that an oversight has occurred here, originating from Equation (6) while expressing pressures in decibels. The group has taken the reference pressure 20 μPa to be equal to –94 decibels. However, the reference pressure is zero in decibels. On this basis, by defining L’U to be the same as LU in Equation (9) and by substituting
 (12)
(12)
the respective identical equations (giving exactly the same equal-loudness-level contours) to Equations (10) and (11) become:
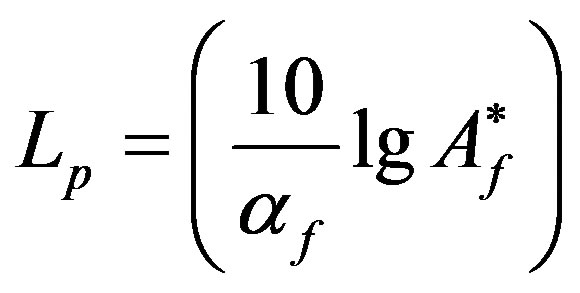 (10’)
(10’)
where

and
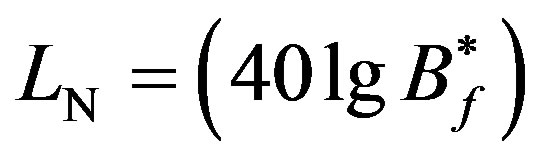 (11’)
(11’)
where
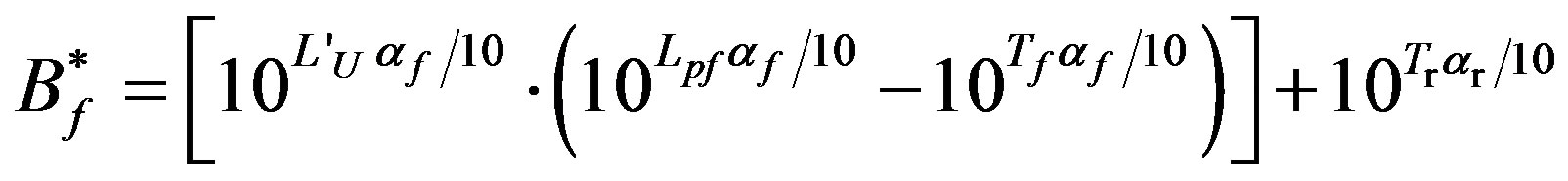
In particular, here Equation (11’) is simpler and clearly more informative than Equation (11) because the chosen loudness function type is formally shown (in brackets) with an explicit dimensional frequency dependent constant showing that the constant terms with high numerical accuracy of Equations (10) and (11) are not a result of the fitting and smoothing processes applied.
On the other hand, something must be amiss in Equation (11’). Namely, by taking into account the originally chosen loudness function type and the discussion concerning Equation (6) above, the following requirement must be fulfilled independently of the frequency band:
 (13)
(13)
resulting in a type of a linear Equation (9) for Equations (10’) and (11’). However, except at 1000 Hz this is not the case (even though as stated in the standard [1]: “LU values were re-estimated by using Equation (C.1) (Equation (1) here) with values of αf”), as can be found by calculating with the tabulated parameter values given in Table 1 [1]. Therefore, the applied loudness function remains unclear and impossible in the standard [1].
Consequently, in addition, although “the contours exhibit a pattern of parallel displacement” [4] (parallel displacement: ΔLN/ΔLp = constant at each frequency band independent of the sound pressure level), Equations (10’) and (11’) do not show such a property generally to hold. In this respect the difference between [1] and the former standard [5] is rather significant. The equal-loudnesslevel contours in [5] exhibit almost wholly a pattern of parallel displacement, as a result of which the author [2] has derived the terms c and θ (at each frequency band) of a loudness function type of Equation (3) (or Equation (1) as well).
On the other hand, it may be possible that the loudness function differs from a simple power function. For example, perhaps the power exponents αf depend on sound pressures. However, such a case cannot be controlled (without any additional definitions) by mathematical fitting methods and solving the parameters for a function, which differs from the chosen basic loudness function.
At 1000 Hz, however, the expression of B*f in Equation (11’) satisfies Equation (13) and the chosen loudness function type reduces to
 (14)
(14)
which results from the assumed loudness function type of Equation (3) with the chosen parameter values at 1000 Hz (c = 1 and θ = αr = 0.250), not depending on the fitting and smoothing methods used to determine the parameters αf and LU at the other frequencies.
Finally, by using the notation (the definition in [1]) 10lg (pr/po)2 = LN ) mentioned in a different form above, loudness level (LN in phons) becomes
 (15)
(15)
confirming that the loudness level in phons of a certain equal-loudness-level contour coincides at 1000 Hz with the sound pressure level expressed in decibels. This seems to be in accordance with the loudness level as defined in the standard [1] and literature: “Value in phons that has the same numerical value as the sound pressure level in decibels of a reference sound, consisting of a frontally incident, sinusoidal plane progressive wave at a frequency of 1000 Hz, which is judged as loud as the given sound.” It is worth noting that the result of Equation (15) seems also to be in accordance with the data (except the threshold contour) shown in [1].
However, something seems to be wrong also here. Namely, Equation (15) includes a phon level value based on a chosen loudness function (Equation (14)) and such a “phon” requires certain rules to be fulfilled. The phon here does not include any defined information concerning the connection between the magnitude of the respective loudness function and the respective phon-level quotation and the physical dB axis (the equal-loudness-level

Table 1. Parameters used to calculate the normal equalloudness-level contours [1].
contour crossing point at the dB axis of 1000 Hz), revealing the subjective sense of the contour complexes upwards and downwards. The connection between the loudness function and the loudness levels are considered next.
3. The Phon Definition and the Magnitude of Loudness
For example, the international standard ISO 532 [6] includes the following relation between the loudness level P in phons and the loudness in sones:
 (16)
(16)
In Equation (16) S is loudness in sones and is designated to be the strength [6] of a sound that is proportional to its subjective magnitude as estimated by normal observers. One sone is the loudness of a sound whose loudness level is 40 phons [6]. Inversely Equation (16) becomes
 (17)
(17)
and thus P is the loudness level in phons. In addition, the standard [6] includes the following notes:
A—When loudness levels are computed from calculated loudness values, the results may differ from those obtained by subjective judgement. It is important, therefore, to state whether the values have been calculated or have been measured by other means.
B—The term phon, without a qualifying abbreviation, should be reserved for the expression of loudness levels determined by direct subjective measurement.
Mathematically the definition (Equations (16) and (17)) of a phon P is rather similar to that of a decibel. The difference is that the logarithm has a base of two (instead of ten), and additionally the definition includes an additive part of 40 phons and a reference value of 1 sone. The latter have a certain meaning, as seen later. Purely mathematically, P only shows the value of the loudness magnitude (the magnitude of the loudness function or its estimate) in powers of two multiplied by ten and with the additive constant 40 phons. Because of the logarithm base and the multiplying factor, P always increases by ten when the loudness magnitude S is doubled.
One can understand here that the properties above of P are purely mathematical and in no way concern the loudness S, which is only required to be positive. Therefore, it is important to see that the loudness problems only concern S (l here) and that any of these problems cannot be solved based on the manner of representing the results (e.g. in phons or any other logarithmic quantity) [2]. The use of logarithmic representations concerning loudness magnitudes seems only to originate from the fact that a loudness function appears to be (in the first approximation, at least) an exponential of the sound pressure level or a power function of sound pressure.
Finally, it should be noted that the two wholly different methods in the standard ISO 532 [6] (the first method by S. S. Stevens, L. Cremer, G. Plenge, and D. Schwarze and the second method by E. Zwicker) both apply the phon definition according to Equation (17) when converting sones to logarithmic loudness levels.
Concerning the “normal observers” or “otologically normal persons” as stated in the standard [1], a sound in sound pressure levels (dB) at 1000 Hz is designated to represent the loudness S of one sone (=40 phons respecttively). Such a sound must be defined for reference purposes (referring to normal hearing) and to fix the respecttive loudness level (and loudness function) unequivocally at the physical dB axis. If such a sound is designated to be 40 dB (representing one sone for otologically normal persons), the logarithmic decibel and phon quantities always coincide at 1000 Hz at 40 dB, so that 40 phon = 40 dB (18)
As a consequence of relation (18), any loudness function shown as a mathematical expression has to be “normalised” to be sensible and comparable with the other methods. In a general case, the normalising procedure only includes the derived or chosen loudness function S (being any type of a function of sound pressure level (SPL)) being given the value of 40 phons (or 1 sone respectively) at 1000 Hz with the argument (SPL) value of 40 dB. The normalising equation is
 (19)
(19)
which is satisfied, in fact, independent of the logarithmic base, only if
 (20)
(20)
where l1000 Hz is the loudness function at the 1000 Hz band and C is a multiplicative constant inside the logarithm depending on the loudness function, not otherwise affecting the loudness function as such by any means.
Concerning Equation (14) above, if it is normalised, C takes the value of 1/10 and the final equation for defining P quotations as a function of sound pressure levels at 1000 Hz becomes
 (21)
(21)
giving 40 phons for the loudness function at 1000 Hz with the sound pressure level of 40 dB as the respective Equation (15) based on the standard [1]. However, the other quotations, e.g. for 30 dB and 50 dB in [1] become, according to Equation (21), the respective quotations 31.7 and 48.3 phons, differing from the value at the crossing point at the dB axis of 1000 Hz.
As mentioned above, the author has derived the equalloudness-level contours in the former standard [5] under the condition that Stevens’ power law (with an exponent θ = αr = 0.3) holds [2]. In [2] the basic loudness function (at 1000 Hz) is quite similar to Equation (14) above, the only difference being that θ was taken to be 0.3 instead of the value of 0.250 in the standard [1]. By replacing 0.250 with 0.3 and approximating, that , the normalising factor C for a function type of Equation (14) becomes
, the normalising factor C for a function type of Equation (14) becomes
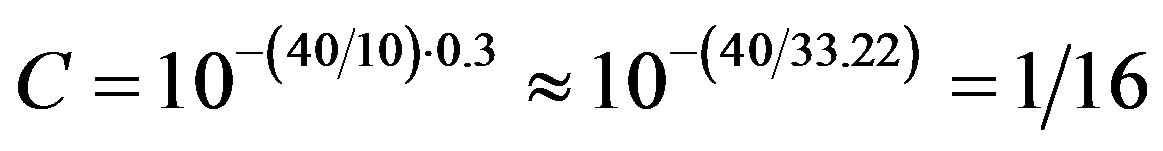
and Equation (21) (in the case of the former standard [5]) then becomes
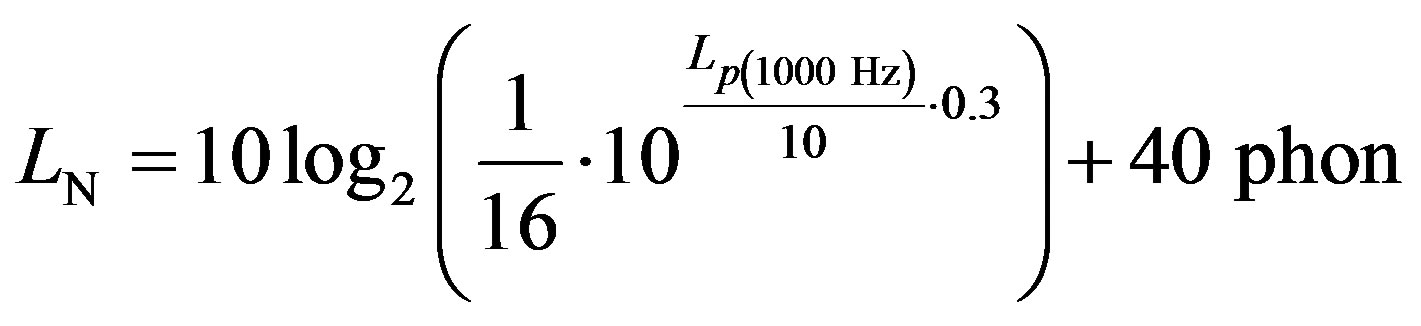 (22)
(22)
In addition by changing the logarithmic base,
 (23)
(23)
which is formally similar to that of Equation (15), giving similar loudness level values for a power function with an exponent of 0.3.
However, only the latter, Equation (23), is consistent with the phon definitions shown in the standard [6], for example. Thus, it seems that the loudness function exponent (αr = 0.250) in the standard [1] has been applied carelessly and erroneously when performing the loudness magnitude conversions. Of course, such conversions must be unequivocally defined. However, this is not the case in [1]. Therefore, clearly something is seriously wrong also with the loudness function and its relation to the phon levels in the standard [1].
Finally, although the changes of the contour shapes may be reasoned, a basic international standard connecting the human auditory perception to all kinds of acoustics, cannot be derived based on a questionable loudness function, including additionally misleading and perplexing mathematical manipulations and elementary misunderstandings about earlier definitions of acoustical terms.
4. Conclusions
Starting by reviewing the chosen loudness function type in the standard ISO 226:2003(E) [1], it has been found that this function does not differ formally from the basic loudness function type given by S. S. Stevens. It has been shown that the fitting and smoothing processes applied in the standard [1] lead to parameter values defining equalloudness-level contours that are not consistent with the chosen loudness function type. The reason for this seems to be that the parameters are fitted to a needlessly complicated form of the basic loudness function.
Several other discrepancies have been observed. The mathematics used in the standard is ambiguous and perplexing. The main equations in the standard [1] seem to include equations in unnecessary forms and puzzling constants. An alternative identical form of the equations has been derived and shown.
Additionally, the phon definition seems to be lacking in the standard [1]. However, when using a mathematical loudness function, the logarithmic representations of such an expression must also be mathematically defined.
Finally, although the changes of the equal-loudnesslevel contour shapes may be well reasoned, this is not the main problem concerning loudness problems. Much more important is the spacing between the contours—explained, in fact, by the loudness function. In this respect the standard [1] clearly differs positively from the former standards.
However, it would be desirable for the discrepancies and oversights in the standard [1] shown here by the author to be taken into account and corrected before publishing a newer version of the standard. It is also recommended that a loudness problem is approached and analysed more exactly and extensively than in the present standard [1]. Of course, the consistency between the final result (the equal-loudness-level contours) and the starting assumptions must hold.
REFERENCES
- International Standardization Organization, “ISO 226: 2003(E): Acoustics—Normal Equal-Loudness-Level Contours,” Geneva, Switzerland.
- J. Parmanen, “A-Weighted Sound Pressure Level as a Loudness/Annoyance Indicator for Environmental Sounds— Could It Be Improved?” Applied Acoustics, Vol. 68, No. 1, 2007, pp. 58-70. doi:10.1016/j.apacoust.2006.02.004
- J. Parmanen, “Erratum: A-Weighted Sound Pressure Level as a Loudness/Annoyance Indicator for Environmental Sounds—Could It Be Improved? [Applied Acoustics, 68 (2007) 58-70],” Applied Acoustics, Vol. 69, No. 2, 2008, p. 183. doi:10.1016/j.apacoust.2006.09.006
- Y. Suzuki and H. Takeshima, “Equal-Loudness-Level Contours for Pure Tones,” Journal of the Acoustical Society of America, Vol. 116, No. 2, 2004, pp. 918-933. doi:10.1121/1.1763601
- International Standardization Organization, “ISO 226:1987 (E): Acoustics—Normal Equal-Loudness-Level Contours,” Geneva, Switzerland.
- International Standardization Organization, “ISO 532:1975 (E): Acoustics—Method For Calculating Loudness Level,” Geneva, Switzerland.

