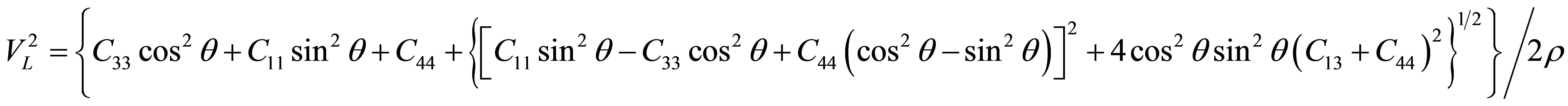Open Journal of Acoustics
Vol.3 No.3(2013), Article ID:36735,9 pages DOI:10.4236/oja.2013.33009
Propagation of Acoustic Wave inside the Carbon Nanotube: Comparative Study with Other Hexagonal Material
Maulana Azad National Institute of Technology, Bhopal, India
Email: s.srivastava.msme@gmail.com
Copyright © 2013 Sanjay Srivastava. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 28, 2012; revised October 30, 2012; accepted November 7, 2012
Keywords: Stiffness; Young’s Modulus; shears Modulus; Secondand third-order Elastic constants; Acoustic velocity
ABSTRACT
Carbon nanotube is a novel and more explored material. In this paper, ultrasonic acoustic velocity of the carbon nanotube has been calculated along unique axis at room temperature. For the evaluations of ultrasonic properties, secondand third-order elastic constants have been computed from Lennard-Jones interaction potential. Attenuation of ultrasonic waves due to phonon-phonon interaction is predominant over thermoelastic loss. Carbon nanotube shows the unique behavior with the chiral number. Chiral number not only affect the band gap and tube radius of the carbon nanotube but also affect the mechanical properties like stiffness, bulk modulus, shear modulus of the tube. The peculiar behavior is obtained at 55˚ due to their least thermal relaxation time and highest Debye average velocity. Results are also compared with other hexagonal metallic materials which present in periods and group of the periodic table. They show the optimum behavior with other hexagonal materials.
1. Introduction
Carbon nanotube (CNT) are cylindrical carbon molecules witch possess novel outstanding better properties (like mechanical, electrical, thermal and chemical properties, 100 times stronger than steel, best field emission emitter, can maintain current density more than 10−9A/cm2, thermal conductivity comparable to that of the diamond) which make then potential useful in a wide variety of the applications (e.g., optical nano-electronics, composite material, conducting polymers, sensor) [1,2]. Nanotubes are composed of sp2 bonds, similar to those observed in graphite and they are naturally aligned themselves into ropes held together by Vander Waals force [3]. Then nono tubes are usually described using the chiral vector, 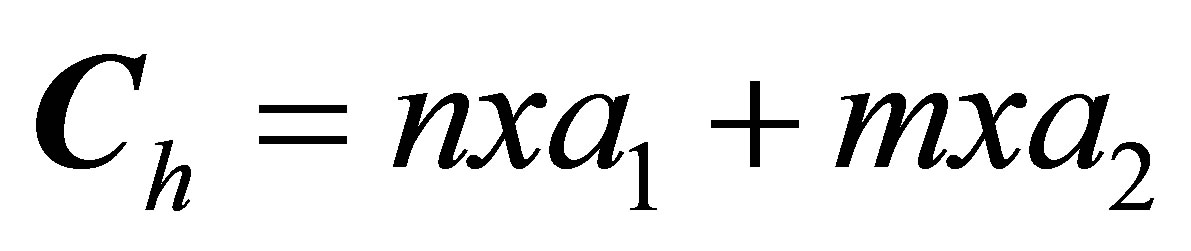 , which connects two crystallographically equivalent sites (A and A¢) on a graphene sheet (where a1 and a2 are unit vectors of the hexagonal honeycomb lattice and n and m are integers). This chiral vector Ch also defines a chiral angle õ, which is the angle between Ch and the zigzag direction of the graphene sheet .Each nanotube topology is usually characterized by these two integer numbers (n, m), thus defining some peculiar symmetries such as armchair (n, n) and zigzag (n, 0) classes. The circumference vector or chiral vector describes the structure of the CNTs. The structure of the single-wall carbon nanotube (except for cap region on both ends) is specified by a vector of original hexagonal (also called hexagonal/honey Comb) lattice called the chiral vector. The unusual high stiffness of CNT makes it suitable ingredients for the application of several composite materials. CNT shows the similar properties as like other hexagonal materials (Ti, Y, Be, Mg, lanthanides ceramic etc.). Wave propagation velocity inside the chosen materials is another key factor in ultrasonic characterization, which in combination with attenuation can provide important tools in understanding, the inspectability of materials; for example, it can provide the information about crystallographic texture, grain sizes, delectability of flaws, and microstructure. Ultrasonic velocity is directly calculated from the elastic constants i.e.
, which connects two crystallographically equivalent sites (A and A¢) on a graphene sheet (where a1 and a2 are unit vectors of the hexagonal honeycomb lattice and n and m are integers). This chiral vector Ch also defines a chiral angle õ, which is the angle between Ch and the zigzag direction of the graphene sheet .Each nanotube topology is usually characterized by these two integer numbers (n, m), thus defining some peculiar symmetries such as armchair (n, n) and zigzag (n, 0) classes. The circumference vector or chiral vector describes the structure of the CNTs. The structure of the single-wall carbon nanotube (except for cap region on both ends) is specified by a vector of original hexagonal (also called hexagonal/honey Comb) lattice called the chiral vector. The unusual high stiffness of CNT makes it suitable ingredients for the application of several composite materials. CNT shows the similar properties as like other hexagonal materials (Ti, Y, Be, Mg, lanthanides ceramic etc.). Wave propagation velocity inside the chosen materials is another key factor in ultrasonic characterization, which in combination with attenuation can provide important tools in understanding, the inspectability of materials; for example, it can provide the information about crystallographic texture, grain sizes, delectability of flaws, and microstructure. Ultrasonic velocity is directly calculated from the elastic constants i.e.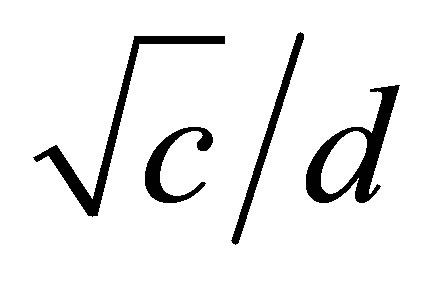
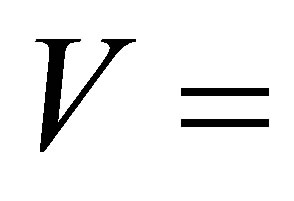 , where C is the elastic constant and d, the density of that particular material. Elastic constants and their variations with temperature provide useful insight into the nature of inter-atomic forces and also give the information of the stability and stiffness of the materials [4,5]. Elastic properties of materials at high pressure and high temperature are of great interest to researchers in many fields, such as physical sciences, earth sciences, and material sciences.
, where C is the elastic constant and d, the density of that particular material. Elastic constants and their variations with temperature provide useful insight into the nature of inter-atomic forces and also give the information of the stability and stiffness of the materials [4,5]. Elastic properties of materials at high pressure and high temperature are of great interest to researchers in many fields, such as physical sciences, earth sciences, and material sciences.
In the present investigation, we have chosen CNTs under the study due to their important features. In the present study, an applied approach for the calculation of second and third order elastic constants of the CNTs validating the interaction potential model was calculated. These nonlinear elastic constants have been used to calculate the ultrasonic velocity and attenuation of the CNTs for their characterization. Their properties were compared with other hexagonal material and optimized results were produced with comparative study.
2. Theory
2.1. Higher Order Elastic Constants
A carbon atom in graphene will assemble in a singlesheet hexagonal lattice resembling the surface of a honeycomb. This is also known as a trigonal-planar σ-bond framework, with an inter-atomic spacing, acc, of approximately 1.41Å along the bonds that are separated by 120 degrees. The 2p electrons from all the atoms on the sheet constitute a cloud of delocalized π-orbital’s surrounding the carbon cores, and these valence electrons, once excited, are responsible for conduction in graphene. Furthermore, multiple sheets of graphene may assemble in stacks, whereby two adjacent sheets are held together weakly by dispersion forces and have an inter-layer spacing of about 3.35 Å. The basis vectors

and

generate the graphene lattice, where a = 0.142 nm is the carbon-carbon bond length. A and B are the two atoms in the unit cell of graphene. The chiral vector begins and ends at equivalent lattice points, so that the particular (n1; n2) tube is formed by rolling up the vector so that its head and tail join, forming a ring around the tube. The length of Ch is thus the circumference of the tube, and the radius is given by the formula
 (1)
(1)
Many of the hexagonal crystals have axial ratio p = c/a different from the ideal value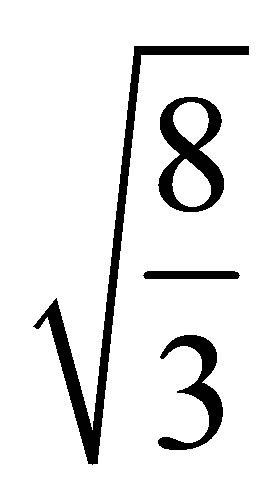 . A good estimate for the lattice parameter in CNT ropes is
. A good estimate for the lattice parameter in CNT ropes is
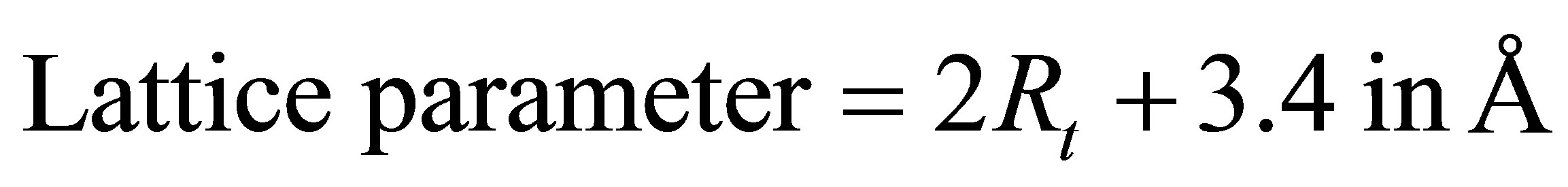 (2)
(2)
Based on the knowledge of higher order elastic constants of the material is essential for the study of the anharmonic properties of solids. Elastic constants also provide insight the nature of binding forces between the atoms since they are represented by the derivatives of the internal energy. A complete set of elastic constants for materials (like second and third order elastic constant) is essential to estimate physical parameters such as Debye temperature, compressibility and acoustic anisotropy. The elastic energy density for a crystal of a cubic symmetry can be expanded up to quartic terms as shown below [6]:
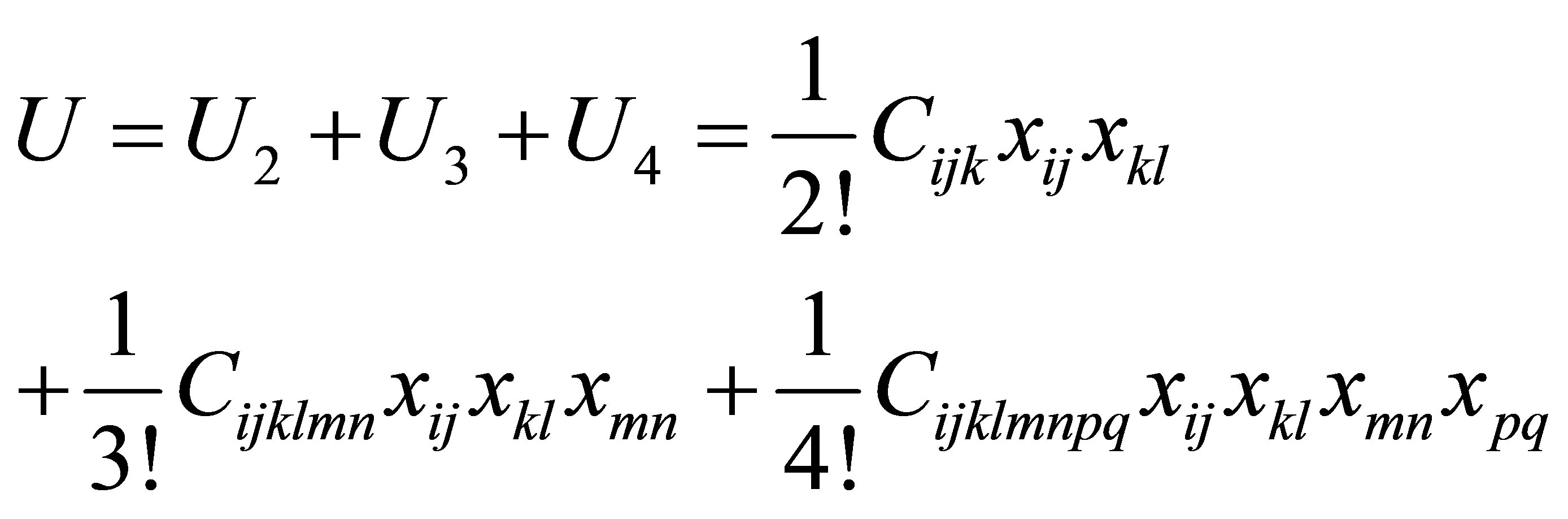 (3)
(3)
where Cijk and Cijklmn are the second and third order elastic constants in tensor form respectively. The second (Cij) and third (Cijk) order elastic constants of material are defined by following expressions.
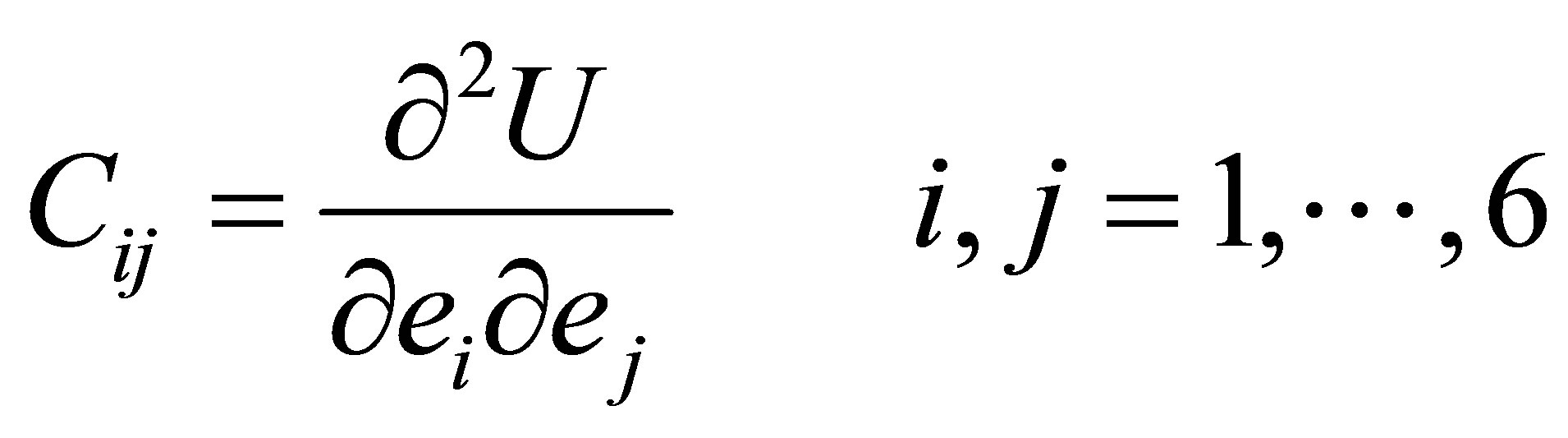 (4)
(4)
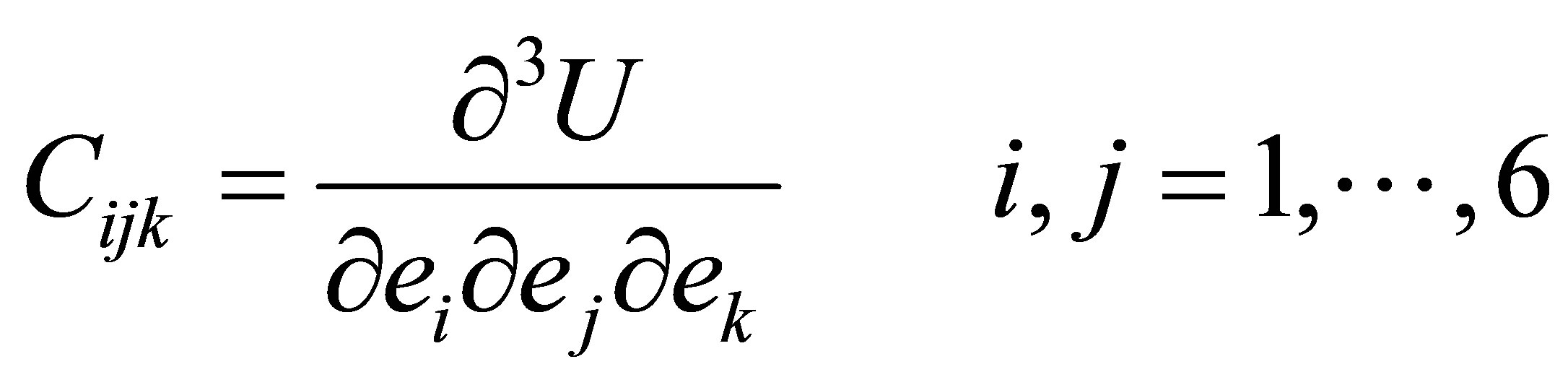 (5)
(5)
where, U is elastic energy density, ei = eij (i or j = x, y, z, ) is component of strain tensor. Equations (1) and (2) leads six second and ten third order elastic constants (SOEC and TOEC) for the hexagonal closed packed structured materials [7]. In present approach, Lennard-Jones interaction potential
) is component of strain tensor. Equations (1) and (2) leads six second and ten third order elastic constants (SOEC and TOEC) for the hexagonal closed packed structured materials [7]. In present approach, Lennard-Jones interaction potential
{ ;
;
where a0, b0 are constants} was utilized due to many body interaction potential. If it is assumed that the basic structure of carbon nanotube is a hexagon then Equation (1) leads following six secondand ten third-order elastic constants.
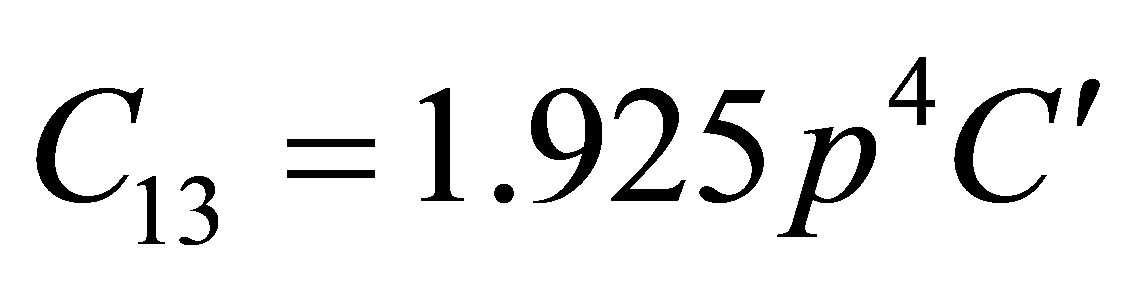

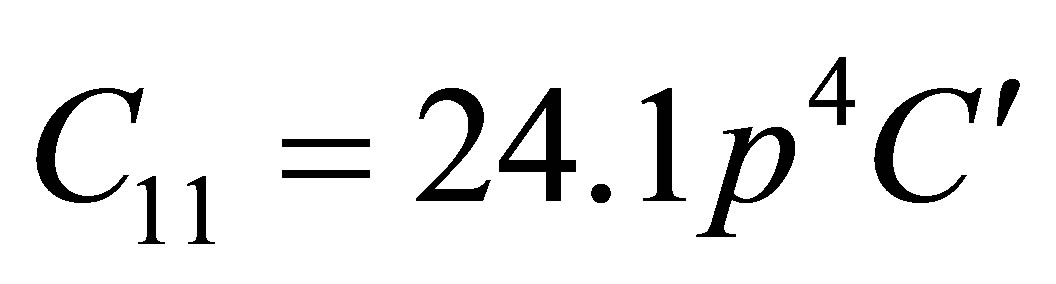

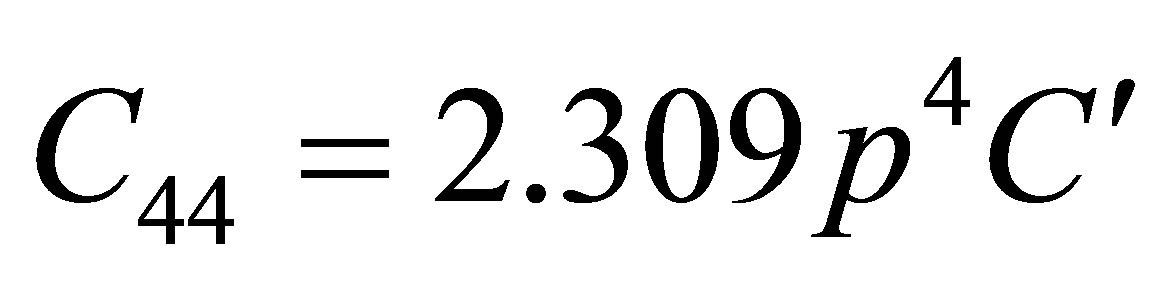
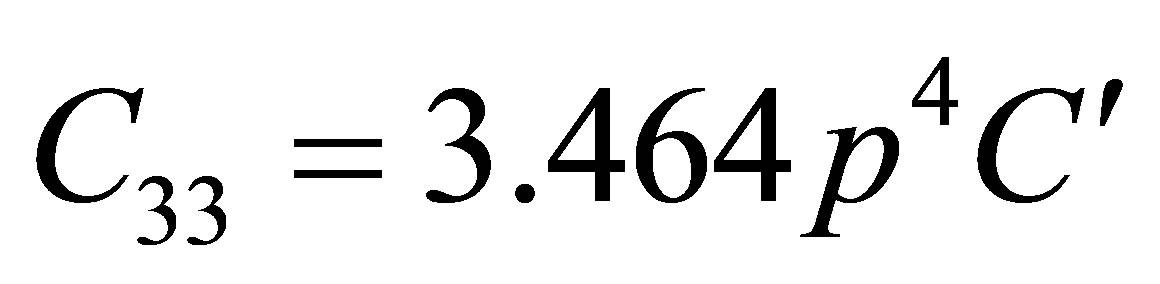



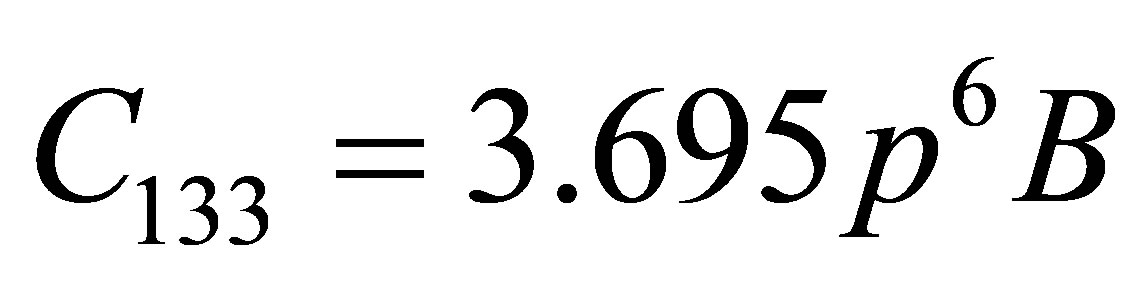
 ,
,
 ,
, 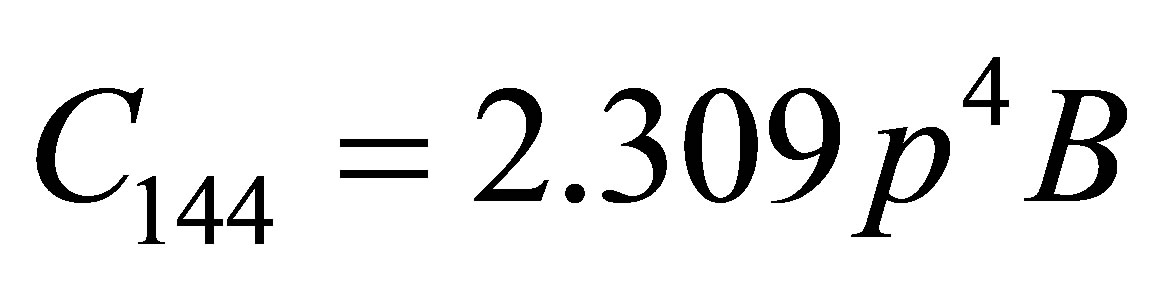 ,
, 
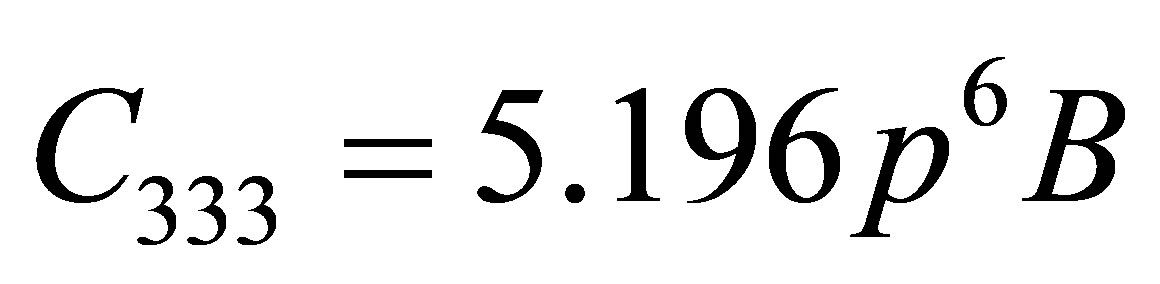

where
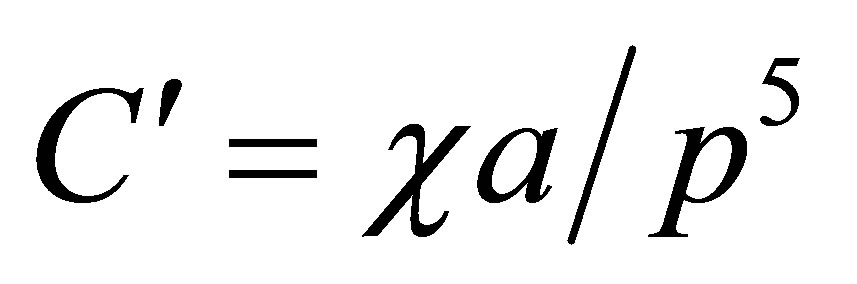 ,
,  ,
,
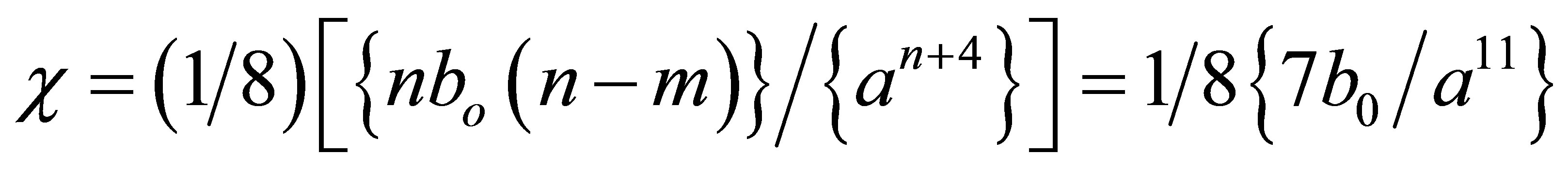 (6)
(6)
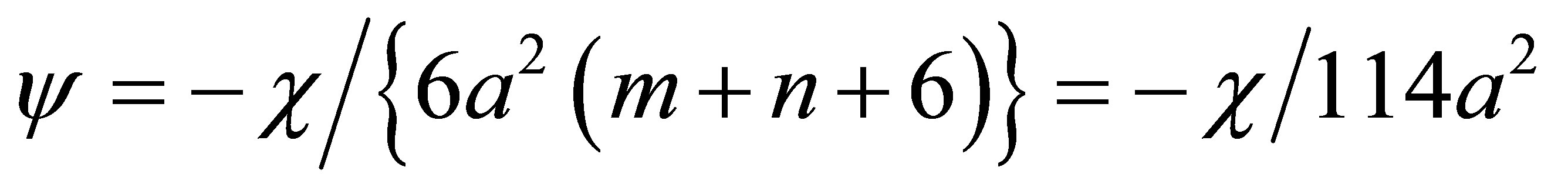
m, n = integer quantity; b0 = Lennard Jones parameter = 6.5 × 10–79 J×m7. p = c/a: axial ratio; c is the height of the unit cell and “a” be the basal plane distance. The symbol “p” is the proposed parameter of axial ratio.
2.2. Ultrasonic Velocity
The secondand third-order elastic constants are related to ultrasonic attenuation through Gruneisen parameters and acoustic coupling constant. On the basis of mode of lattice vibration, there are three types of velocities (longitudinal, quasi shear and shear) in acoustical region [8]. The ultrasonic velocities can be computed using calculated values of second-order elastic constants. These velocities depend on the direction of propagation of wave from the unique axis of hexagonal crystal [9]. The ultrasonic velocities as a function of angle between direction of propagation and unique axis for hexagonal structured materials are given as follows [10]:
 (7)
(7)
where VL, VS1 and VS2 are longitudinal, quasi shear and pure shear wave ultrasonic velocities. Variables ρ and θ represent the density of the material and angle with the unique axis of the crystal respectively. The Debye average velocity (VD) is useful to study the Debye temperature and thermal relaxation time of the materials. The Debye temperature (TD) is an important physical parameter of solids, which differentiate the classical and quantum behavior of phonon [11]. The following expressions have been used for the evaluation of Debye average velocity and Debye temperature
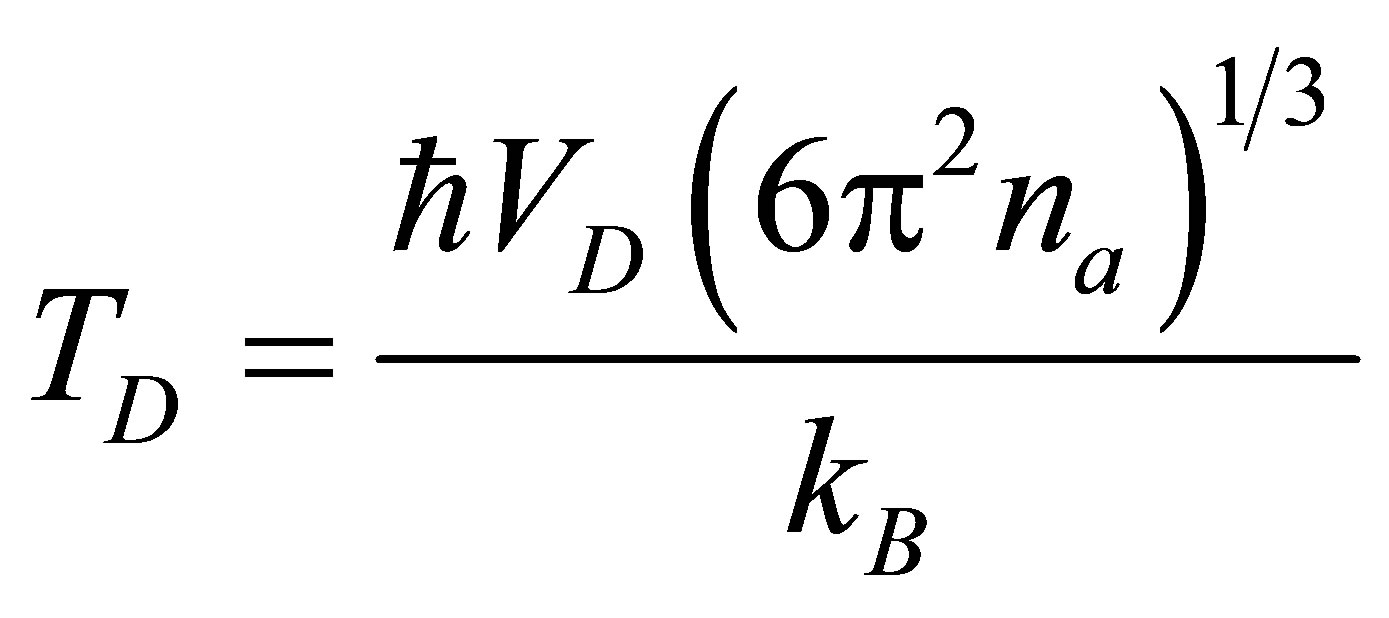 (8)
(8)
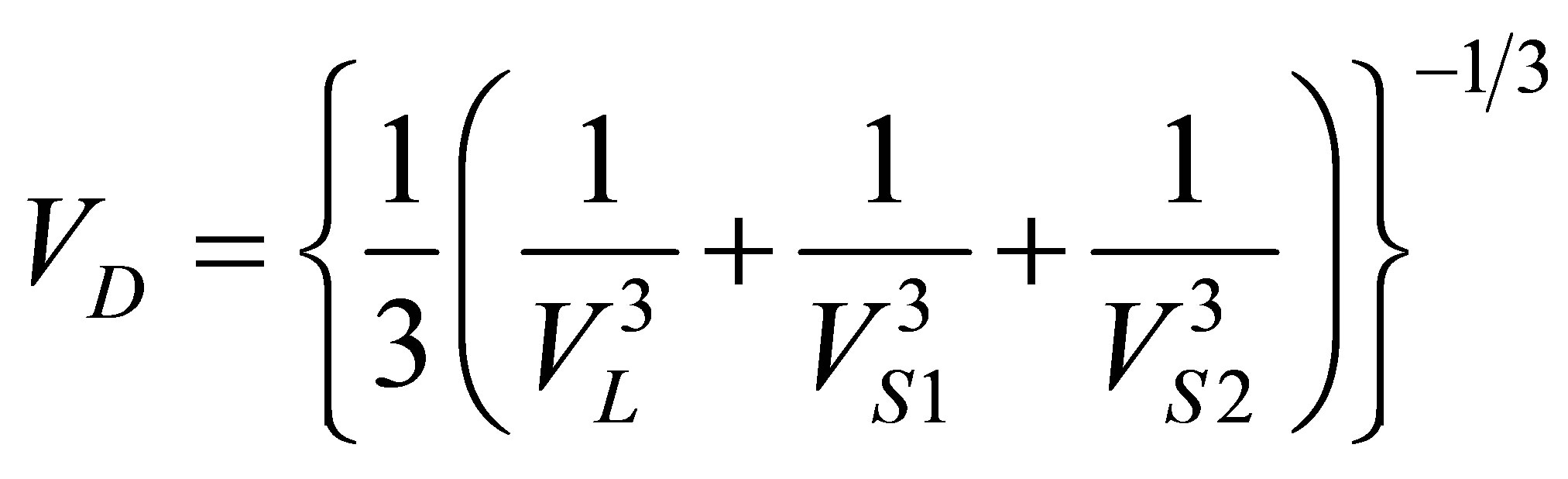 (9)
(9)
3. Results and Discussion
In order to examine the band structure, conductivity and wave propagation inside the nanotube, it is necessary to derive its ε-k relation. The hexagonal unit cell is characterized by a = b ≠ c, α = β = 90˚, γ = 120˚. The unit cell is a parallellopiped by height c with a base which is a rhombus of side “a”. A hexagonal crystal has one sixfold axis of symmetry. All belong to the crystal class P63/mmc. The ideal c/a ratio required for close packing of spheres to form the HCP structure is 1.633 (i.e. ). The tube radius is calculated from the equation (1). Figure 1 shows the variation of tube radius with chiral number. In curve n1 = varied but n2 is assumed to be zero, n1 – n2 is the divisible of 3 (where n1 and n2 are the chiral number of the CNT either in zigzag structure or armchair structute). Hence, the tube is zigzag in nature and they show metallic in character. In zigzag structure, the chiral vector is oriented along the axis, hence in this case the chiral angle i.e., ζ = 0˚. In case of arm chair structure, the chiral number is equal, but it is not zero. The behaviour is again found in metallic nature, as shown in Figure 1(b). In Figure 1(c), the difference is not the divisible of 3; the found structure may be either zigzag or armchair. However the behaviour of the CNT is to be changed from metallic to semiconducting in nature, while the bond angle ζ is 30˚. The variation of the band bap with tube radius and chiral number in semiconducting CNT is shown in Figure 2. These band gaps are calculated from the following formula:
). The tube radius is calculated from the equation (1). Figure 1 shows the variation of tube radius with chiral number. In curve n1 = varied but n2 is assumed to be zero, n1 – n2 is the divisible of 3 (where n1 and n2 are the chiral number of the CNT either in zigzag structure or armchair structute). Hence, the tube is zigzag in nature and they show metallic in character. In zigzag structure, the chiral vector is oriented along the axis, hence in this case the chiral angle i.e., ζ = 0˚. In case of arm chair structure, the chiral number is equal, but it is not zero. The behaviour is again found in metallic nature, as shown in Figure 1(b). In Figure 1(c), the difference is not the divisible of 3; the found structure may be either zigzag or armchair. However the behaviour of the CNT is to be changed from metallic to semiconducting in nature, while the bond angle ζ is 30˚. The variation of the band bap with tube radius and chiral number in semiconducting CNT is shown in Figure 2. These band gaps are calculated from the following formula:

The band gap of semiconducting CNT decreases with increase the tube radius as well as chiral number. Knowledge of the carbon nanotube dispersion relation allows one to identify whether a tube produces metallic or semiconducting behaviour, and in the latter case, determine the conduction and valence band edges and thus the band gap [12,13]. Typical values for the band gap are in the range of tenths of an electron-volt to a few electron-volts, and for the previously mentioned (16, 0) tube it is ~0:62 eV. The parameters “Rt” for SWCNT (10, 10) is 6.7834 Å. Hence the lattice parameter “a” becomes equal to 16.9664 Å. By applying the symmetric operation, it is also found that C11 = C22, C33, C44 = C55, C12, C13= C23, and C66 can be obtained by measuring the velocity in c-direction (six fold symmetry axis). The constants C11, C33 and C44 have been determined from the direct relation, Cij = ρV2, where V is the relevant sound velocity. They are related with equation (7). Seven velocity measurements enable us to determine all the seven second-order
|
|

Figure 1. Variation of Tube radius with chiral number for different values of n1 and n2.

Figure 2. Variation of Tube radius and Eg with chiral number (n1 = 6 n2 = integers but not divisible by 3 and ζ).
elastic constants. This is metallic in character and ultrasonic attenuation is due to phonon-phonon interaction. The SOECs and TOECs of SWCNT are calculated by using lattice parameter and set of equations (2) for (10, 10) chiral system, their results are tabulated in Table 1. Furthermore, the following physical parameters have been also determined from set of equation. The other parameter was calculated from following formula by the evaluation of the C11, C12, C13, C33, C44, and C66:
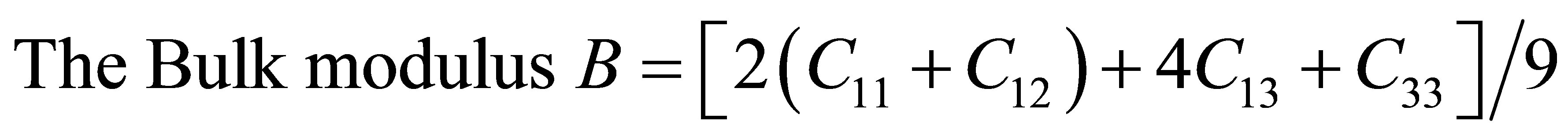 ,
,
 ,
,
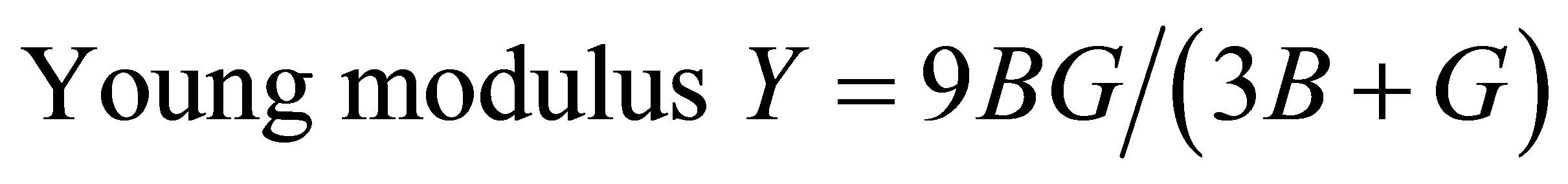
poission’s ratio 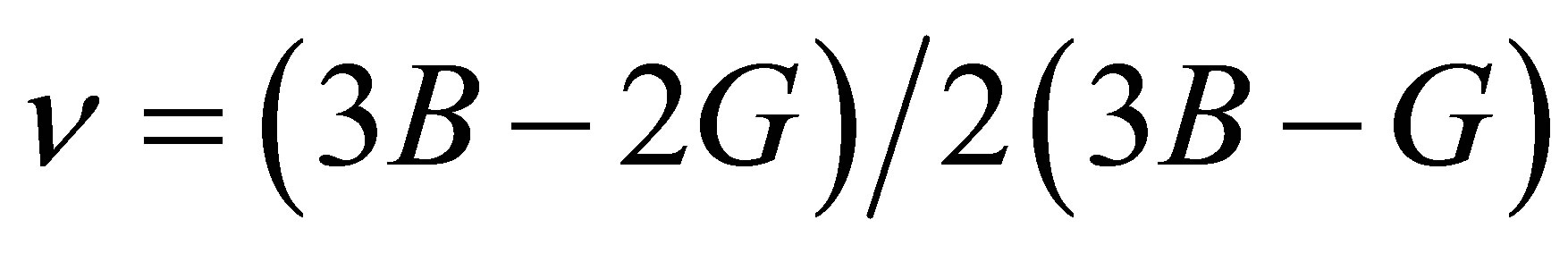 using second order elastic constants, which are tabulated in Table 1. The values of six independent elastic constants along with dependent variable were evaluated by calculating the stress tensors on different deformations applied to the equilibrium lattice of the hexagonal unit cell.
using second order elastic constants, which are tabulated in Table 1. The values of six independent elastic constants along with dependent variable were evaluated by calculating the stress tensors on different deformations applied to the equilibrium lattice of the hexagonal unit cell.
All these elastic constants are positive and satisfy the well-known Born’s criteria for mechanically stable hexagonal crystals: C11 > 0, (C11 − C12) > 0, C44 > 0, and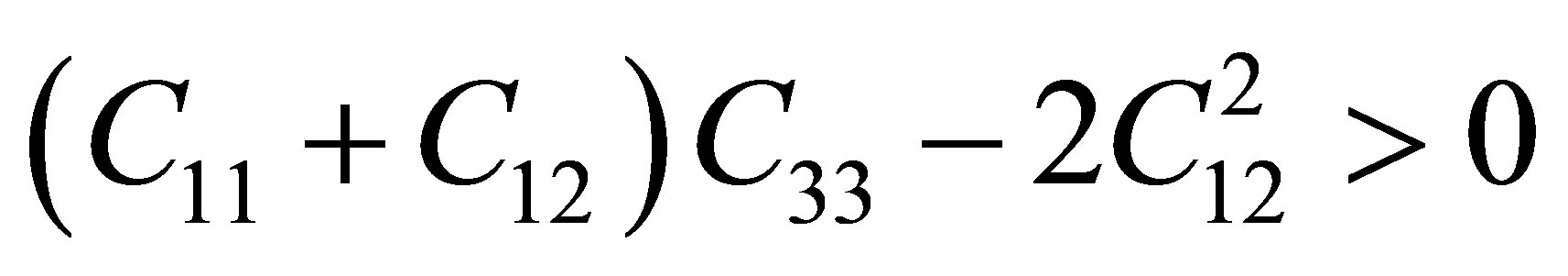 . The variation of the elastic constant with chiral number is shown in Figure 3. With increase the chiral number, the elastic constant decrease from higher to sudden lower values. Beyond (6, 10), the values becomes constant with increase the chiral number. For zigzag structure, the maximum values are at higher chiral number, but the optimum and useful values are found from n1 = 12 to n1 = 21.
. The variation of the elastic constant with chiral number is shown in Figure 3. With increase the chiral number, the elastic constant decrease from higher to sudden lower values. Beyond (6, 10), the values becomes constant with increase the chiral number. For zigzag structure, the maximum values are at higher chiral number, but the optimum and useful values are found from n1 = 12 to n1 = 21.
The beautiful results are tabulated in Table 2 for different chiral number. The ultrasonic velocities are evaluated using elastic constants and density which in turn provides Debye average velocity in all chosen materials. The variations of all the three types of velocity are shown in Figure 4. With increase the angle from, the longitudinal velocity increases from 0˚ to 60˚ but again decrease with increase the angle of propagation. But shear velocity in direction-1 show the same effect in the opposite direction.
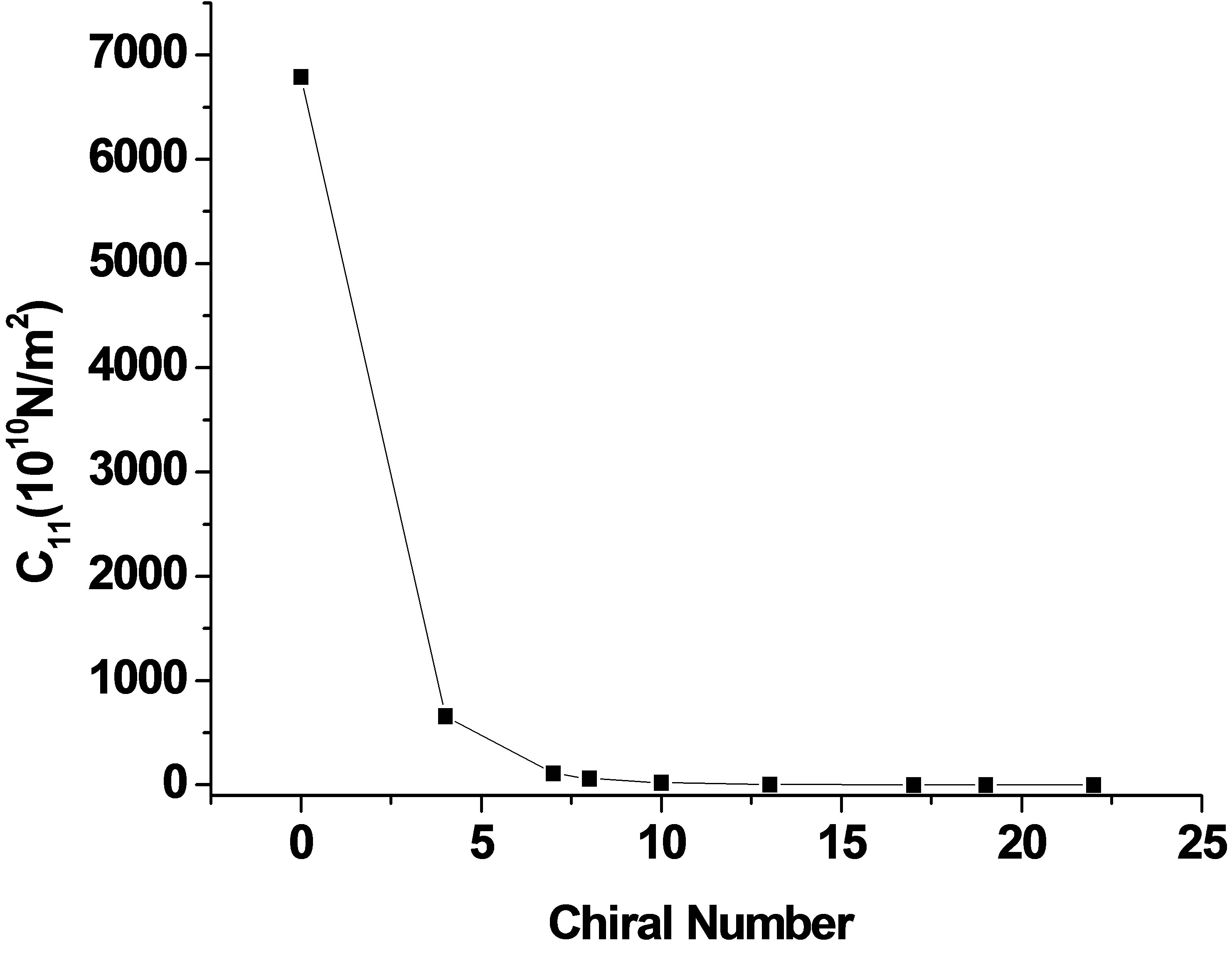
Figure 3. Variation of C11 with chiral number (n1 = 6 n2 = integers but not divisible by 3 and ζ).

Figure 4. Variation of longitudinal, shear (1) and shear (2) vs. angle with unique axis of crystal.

Table 1. SOECs (GPa) and TOECs (GPa) of SWCNT at room temperature.
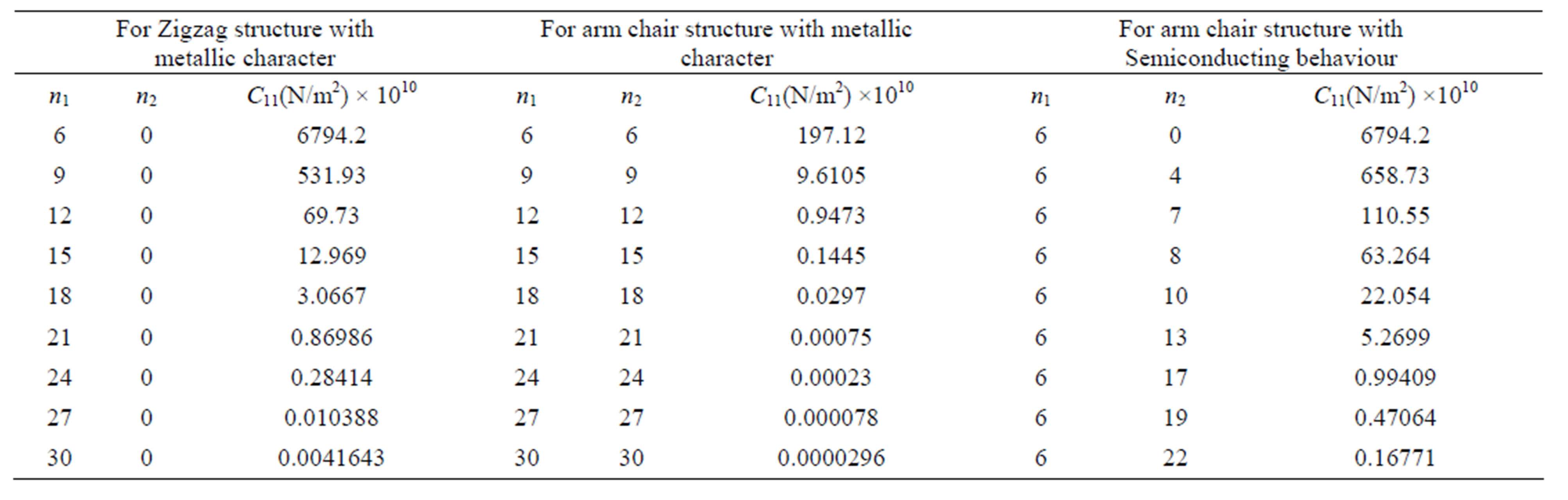
Table 2. Stiffness with chiral number.
The shear velocity in direction-2 continuously increases with angle. The plot of average Debye VD (Figure 5) for the propagation of wave at different angles with unique axis show large variation with change in angle. This is the combined effect of the all the three velocity which depends upon the second order elastic and the density of the materials. The SWCNT shows the similar effect of the velocity propagation like other the other hexagonal materials. There are different types of the hexagonal materials which are classified in a different group and periods in the periodic table. They may be in s, p d and f block element. The ideal values c/a is 1.633. Be and Mg (p = 1.56803 for Be and Mg 1.62350) are the s-block elements, Ti, Y, Zr, and Hf, Re, Os, d-block member and from La to Tm are f-block elements. Only Tl is the p-block elements. For investigating the wave propagation in the material, the density decides its nature. The unit cell parameters “a” and “p” for Gd, Tb, Dy, Ho, Er and Tm are 3.63Å, 3.60Å, 3.59Å, 3.58 Å, 3.56Å, 3.54Å and 1.592, 1.583, 1.574, 1.570, 1.570, 1.571 respectively. The value of m, n and b0 for these lanthanides metals are 6, 7 and 2.3 × 10−64 erg cm7 correspondingly. Three metals La, Pr and Nd have the DHCP (double HCP) structure where the stacking of close packed planes follows the order ABACABAC instead of the usual HCP sequence ABAB [14]. Consequently, close packing under these conditions leads to an ideal c/a ratio of 3.3256. Overall, most of the metals were lower and within −0.1 of their ideal c/a ratio, except for Cd and Zn which exceeded the ratio by 0.223 and 0.194, respectively. In case of transition metal like Ti, Y, Zr, and Hf, the SOEC shows the irregular behavior due involvement of 4f orbital. In case of heavy rare earth elements, the SOEC

Figure 5. Variation average Debye velocity vs. angle with unique axis of crystal.
are found to be increasing from metal Gd to Tm. Thus the thermal softening behaviors are obtained as we move from Tm to Gd. These metals have low bulk modulus and higher order elastic constants in comparison to other hexagonal structured material [7-10,12,13]. This reveals that large strain will develop for a given deforming force in these materials. Figure 6 shows the variation of average Debye velocity vs. angle with unique axis of crystal and compare with alkaline earth metal like Be and Mg (because they possess HCP crystals structure). The velocity of propagation in medium depends upon the elastic constant, and density of the materials [15].
The density of the carbon nanotube is much similar to these metals but their second order elastic constant four
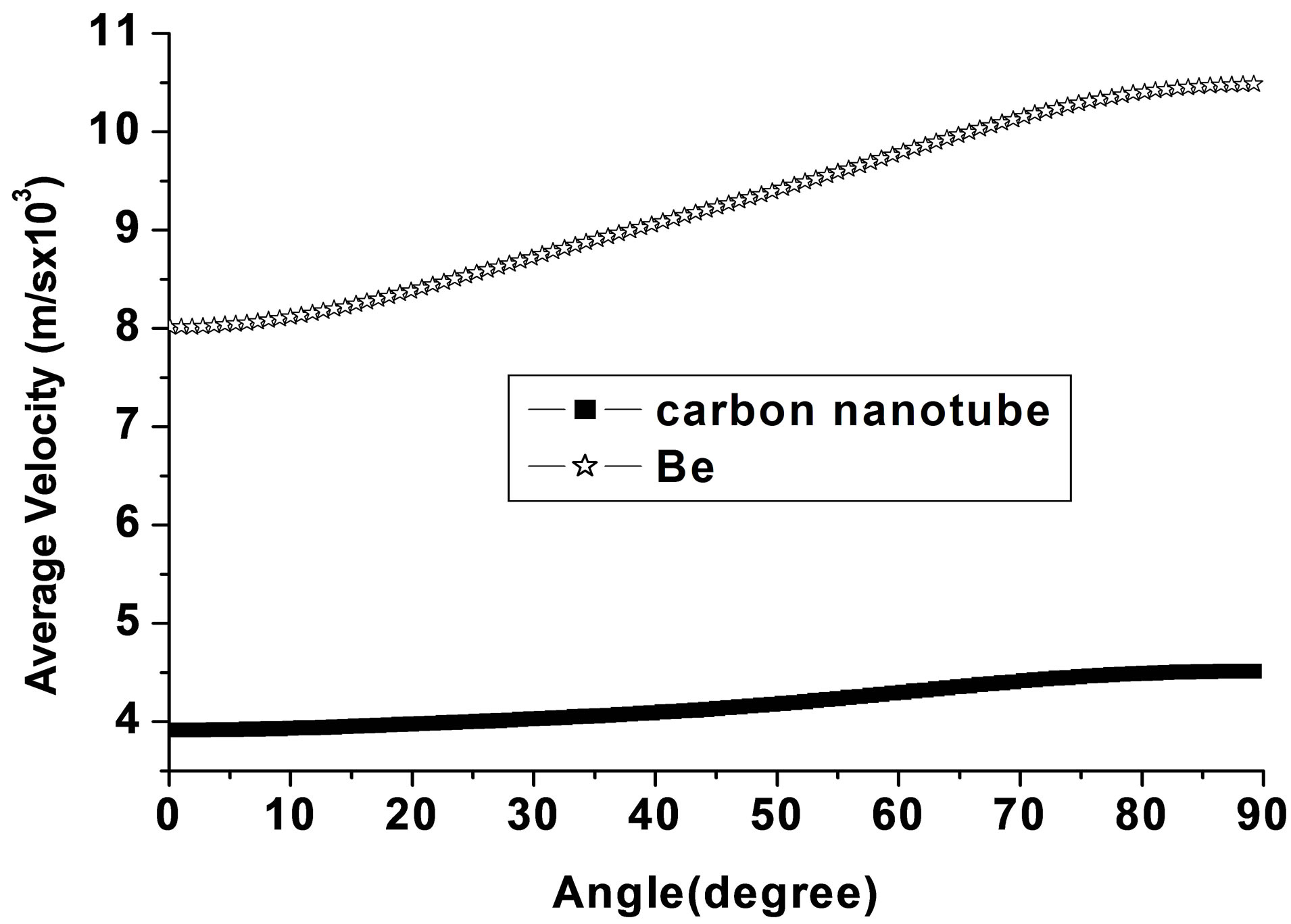
Figure 6. Variation average Debye velocity vs. angle with unique axis of crystal and compare with alkaline earth metal (Be, ρ = 1.85 × 103 kg/m3, and elastic constant C11 = 292, C12 = 24, C33 = 349, C44 = 163, C66 = 6 GPa).
to five times less than “Be” but similar to Mg. it is evident from the Figure 6 that the propagating velocity inside the Carbon nanotude is two times less than the Be crystal structure. Ti, Co, and Zn belong in 3d series and Y and Zr in 4d series but they possess HCP crystal structure. The variation of the average velocity with propagating angle along the unique axis is presented in the Figure 7. The density as well as second order elastic constant of the Ti and Y is high as carbon nanotube but the velocity of propagation along the crystals axis shows negative effect. To compare with carbon nanotube the average velocity in Ti decrease with increasing angle, as evident from Figure 7(a). Y show similar effect as Ti, compared with the Figure 7(b). Hf is the member of d-block (5d) element like Ti, Y and also possesses the same crystals structure but they show dramatic effect on the propagation of acoustic wave inside the materials. In this material, the average Debye velocity decreases with the angle and attain the minimum value around 45˚ - 55˚ and then increase with the angle, as shown in Figure 8. Hf also possesses higher density (9 - 10 times heavy from the carbon nanotube) as compared to carbon nanotube. Due to higher density, they show lower propagating velocity inside the materials. Due to involvement of 4f orbital in Hf and also expected double crystal structure the propagating velocity along axis, they show negative effect from the Ti, and Y. Re is again the member of the 5d series and exhibits the same crystal structure, but their trends for propagating velocity inside the materials show positive effect from the Hf , Ti and Zr. Figure 9 shows the variation of average Debye velocity with the propagating axis. It is evident from the Figure 9 that the velocity first decreases and attains the minimum values and then increase with increase the angle. Due to their high density (19 - 20 times heavy from the carbon nanotube) and very high elastic constant as compared to the known
 (a)
(a)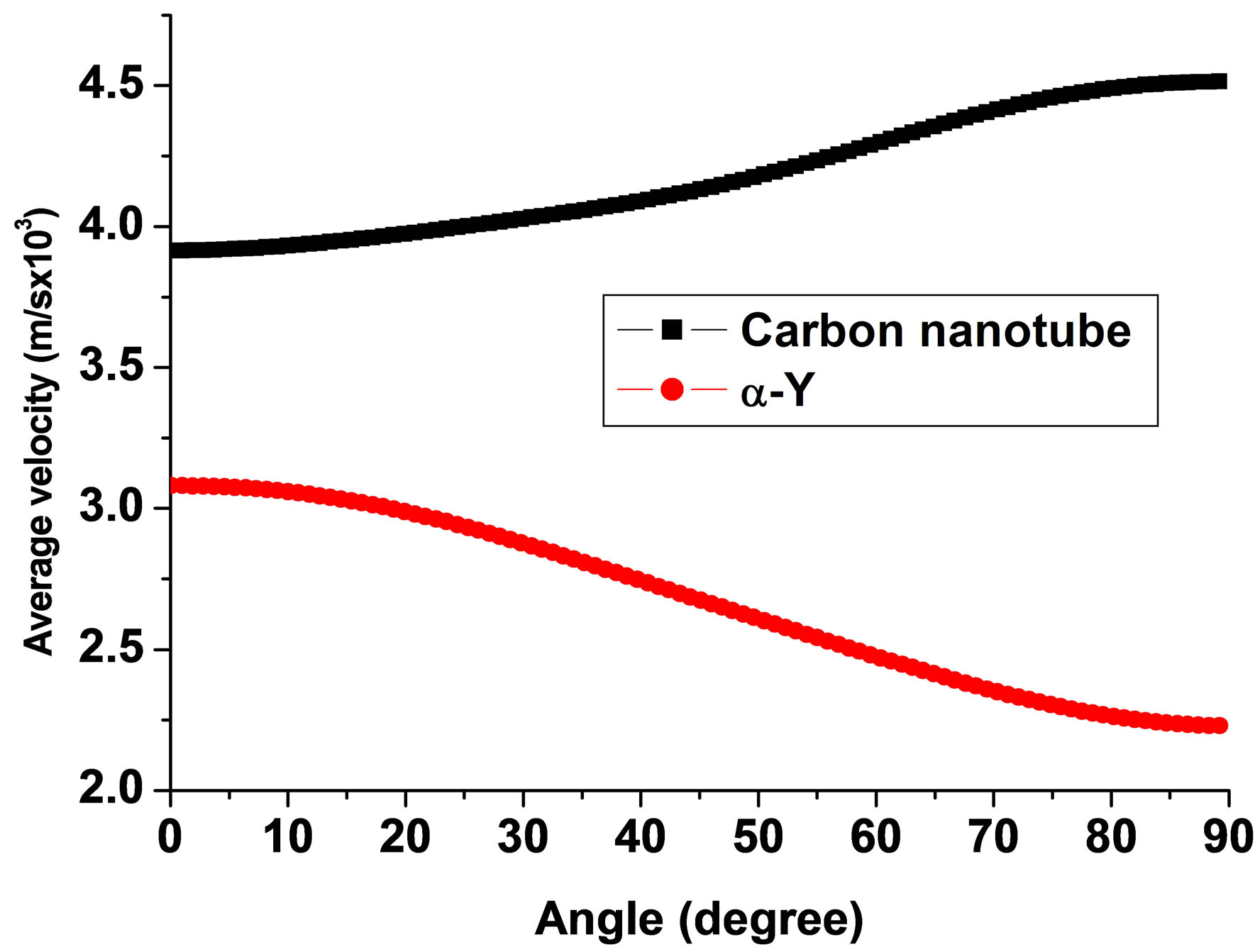 (b)
(b)
Figure 7. Variation average Debye velocity vs. angle with unique axis of crystal and compare with transition metal (a: Ti, ρ = 4.51 × 103 kg/m3, and elastic constant C11 = 160, C12 = 90, C33 = 181, C44 = 46.5, C66 = 66 and b: Y, ρ = 4.47 × 103 kg/m3, and elastic constant C11 = 77.9, C12 = 29.2, C33 = 76.9, C44 = 24.3, C66 = 20 GPa).

Figure 8. Variation average Debye velocity vs. angle with unique axis of crystal and compare with transition metal (Hf, ρ = 13.1 × 103 kg/m3, and elastic constant C11 = 181, C12 = 77, C33 = 197, C44 = 55.7, C66 = 66 GPa).

Figure 9. Variation average Debye velocity vs. angle with unique axis of crystal and compare with transition metal (Re, ρ = 21 × 103 kg/m3, and elastic constant C11 = 616, C12 = 273, C33 = 683, C44 = 161, C66 = 206 GPa).
metal in HCP crystals structure expect Os, they exhibit lower velocity because of density effect, evaluated from equation (7).
In periodic table and known HCP crystal structure, Os is the heaviest element among all the elements. Figure 10 shows the variation of average Debye velocity with propagating angle along the crystal axis. It can be seen from the Figure 10 that the velocity decrease with increase the angle, beyond attending the minimum velocity they again increase. Out of the various materials studied in this research work, they possess the higher values because of the higher elastic constant along with the maximum density (18 - 20 times more than the carbon nanotube).
The group Os, Ru, Re, Be and Co exhibit the highest moduli of all the HCP metals. All show a pronounced maximum value of E on the basal plane, for which θ is zero, and a tendency by Ru, Re and Co to exhibit a minimum between 0 < θ < 90. With the exception of Be, the G-behaviour exhibits a minimum when θ is zero and 90˚, and a maximum for 0o < θ < 90˚. In the case of Be, a maximum G occurs when θ is zero, indicating G is highest on the basal plane. The elastic constants are important since they are related to hardness and are used for the determination of the ultrasonic velocity. The plot of VD (Figure 11(a)) for the propagation of wave at different angles with unique axis implies that these metals have slight variation in velocity for each direction of propagation and have maxima at θ = 55˚. Fig.11b shows the variation of the average velocity with crystals axis or the rare earth elements along with carbon nanotube. Lanthanides possess higher velocity with carbon nanotube because of similar elastic constant and heavier density. Carbon nanotube is the allotrope of the carbon and Tl belongs to the same family. The pπ-pπ interaction provides the propagation of the velocity inside the metal.
In other case, sσ-sσ, dπ-sπ dπ-dπ, dπ-fπ and fπ-fπ are

Figure 10. Variation average Debye velocity vs. angle with unique axis of crystal and compare with transition metal (Re, ρ = 22.61 × 103 g/m3, and elastic constant C11 = 765, C12 = 229, C33 = 846, C44 = 270, C66 = 219 GPa).
 (a)
(a)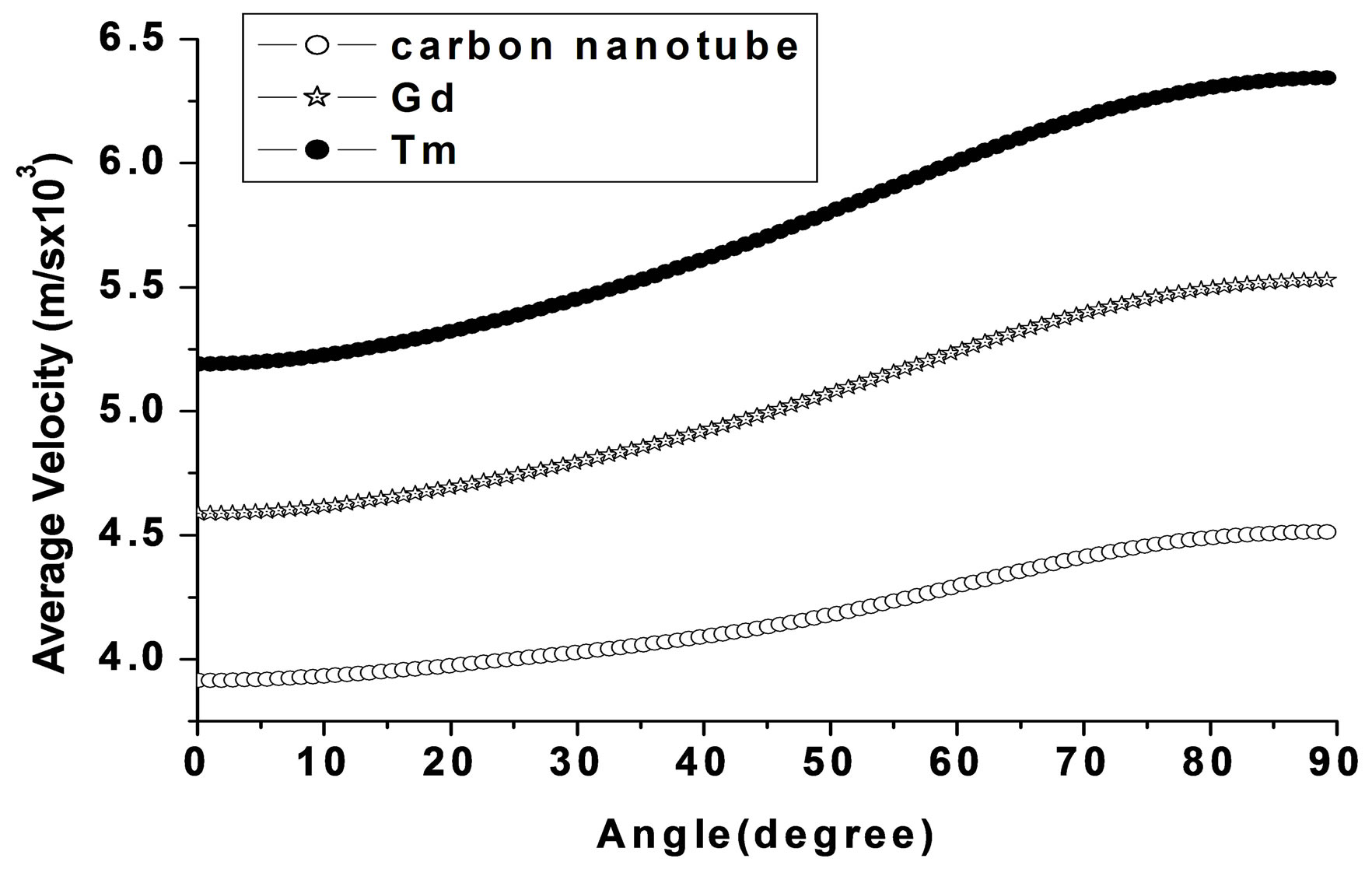 (b)
(b)
Figure 11. Variation average Debye velocity vs. angle with unique axis of crystal of (a) Heavy rare earth elements and (b) compare with carbon nanotube.
the responsible factor for the propagating the acoustic wave inside the material. In case of metal either from the s, d or f-block, they bear the maximum lattice vibration from the initial stage due to interaction with the acoustic wave. The dominant mechanism for ultrasonic attenuation in these metals is phonon-phonon interaction. But the carbon nanotube shows the adverse effect because of planar hexagon structure. Another predominant effect which lowers the propagation of the acoustic wave inside the carbon naotube is the localization of the bound electron in the bonding state. Its propagation can be compared with Tl, because of the same member. They are much heavier and possess same stiff. Their variation of velocity with angle is shown in Figure 11. It is evident from the Figure 12 that they show two humps at the different angle, and also show the lower velocity with cabon nanotude.
4. Conclusion
On the basis of the above study, the following conclusions have been drawn:
1) Carbon nanotube are characterized by the chiral number and tube radius increase but band gap of the carbon tube decrease decreases with increasing the chiral number.
2) Lennard-Jones interaction potential was used to calculate the second and third stiffness of the carbon nanotube.
3) A detailed study of the elastic properties of carbon nanotube gives complete set of second order elastic stiffness constants, compliance constants, Poisson’s ratios, volume compressibility and bulk modulus of this crystal. All these important parameters for this crystal are measured and tabulated. The elastic anisotropy of various parameters like phase velocity, slowness, Young’s modulus and linear compressibility are depicted in the form of two dimensional surface plots.
4) The mechanical property of the carbon nanotube depends upon chirality of the carbon nanotube and decreases with increasing the number. Also it is found that C33 is less than C11, which corresponds to the binding forces along the basal plane of the crystal. Second and

Figure 12. Variation average Debye velocity vs. angle with unique axis of crystal and compare with p-block-metal (Re, ρ = 11.85 × 103 kg/m3, and elastic constant C11 = 765, C12 = 229, C33 = 846, C44 = 270, C66 = 219 GPa).
third order elastic constant are utilized to determine the Debye average velocity.
5) Therefore, in carbon nanotube, the bonding between the atoms along the a-b plane is stronger than that between the atoms along the c-direction. Not only this parameter, but also second and third order parameter gives the same indication. The anisotropic properties of SWCNTs calculated with the help from second order elastic constant are well related with the ultrasonic velocities as well as with the higher order elastic constants.
6) The highest change in Debye average was observed at 50˚ - 55˚along the unique axis.
7) Due to change in bonding from metal to SWCNT, the observed changes in velocity with different type of the metal along with CNT are different at the different angle. Their values depend upon the phonon-phonon vibration in the lattice.
8) In metallic material, phonon-phonon vibration is easily achieved due acoustic wave interaction as compared to CNT because of less tightly packing.
REFERENCES
- A. Javey, H. Kim, M. Brink, Q. Wang, A. Ural, J. Guo, P. Mcientyre, P. McEuen, M. Lundstrom and H. Dai, “High K-Dielectric for Advanced Carbon Nanotube Transistors and Logic Gates,” Nature Materials, Vol. 1, No. 1, 2002, pp. 241-246.
- J. Wildoer, L. Venema, A. Rinzler, R. Smalley and C. Dekker, “Electronic Structure of Atomically Resolved Carbon Nanotubes,” Nature, Vol. 391, No. 6662, 1998, pp. 59-62. doi:10.1038/34139
- R. Bacon, “Growth, Structure, and Properties of Graphite Whiskers,” Journal of Applied Physics, Vol. 31, No. 2, 1960, pp. 283-290. doi:10.1063/1.1735559
- Y.-H. Li and J.-T. Lue, “Dielectric Constants of Single-Wall Carbon Nanotubes at Various Frequencies” Journal of Nanoscience and Nanotechnology, Vol. 7, No. 8, 2007, pp. 1-4.
- M. Rosen, “Elastic Moduli and Ultrasonic Attenuation of Gd, Tb, Dy, Ho and Eb from 4.2 to 300K,” Physical Review, Vol. 174, No. 2, 1968, pp. 504-514. doi:10.1103/PhysRev.174.504
- Kailash, K. M. Raju, S. K. Shrivastava and K. S. Kushwaha, “Anharmonic Properties of Rocksalt Structure Solids,” Physica B: Condensed Matter, Vol. 390, No. 1-2, 2007, pp, 270-280. doi:10.1016/j.physb.2006.08.024
- A. K. Yadav, R. R. Yadav, D. K. Pandey and D. Singh, “Ultrasonic Study of Fission Products Precipitated in the Nuclear Fuel,” Materials Letters, Vol. 62, No. 17-18, 2008, pp. 3258-3261. doi:10.1016/j.matlet.2008.02.036
- C. Oligschleger, R. O. Jones, S. M. Reimann and H. R. Schober, “Model Interatomic Potential for Simulations in Selenium,” Physical Review B, Vol. 53, No. 10, 1996, pp. 6165-6173. doi:10.1103/PhysRevB.53.6165
- D. K. Pandey, D. Singh and R. R. Yadav, “Ultrasonic Wave Propagation in 3rd Group Nitrides,” Applied Acoustics, Vol. 68, No. 7, 2007, pp. 766-777. doi:10.1016/j.apacoust.2006.04.004
- D. K. Pandey, P. K. Yadawa and R. R. Yadav, “Acoustic Wave Propagation in Laves-Phase Compounds,” Materials Letters, Vol. 61, No. 25, 2007, pp. 4747-4751. doi:10.1016/j.matlet.2007.03.031
- Cz. Jasiukiewicz and V. Karpus, “Debye Temperature of Cubic Crystals,” Solid State Communications, Vol. 128, No. 5, 2003, pp. 167-169.
- H. J. Chen, Q. Z. Xue, Q. B. Zheng, J. Xie and K. Y. Yan, “Influence of Nanotube Chirality, Temperature, and Chemical Modification on the Interfacial Bonding between Carbon Nanotubes and Polyphenylacetylene,” The Journal of Physical Chemistry C, Vol. 112, No. 2, 2008, pp. 16514-16520.
- G. H. Gao, T. Cagin and W. A. Goddard, “Energetics, Structure, Mechanical and Vibrational Properties of Single-walled Carbon Nanotubes,” Nanotechnology, Vol. 9, No. 3, 1998, pp. 184-191.
- A. Nareth, “Nuclear Magnetic Resonance in Hexagonal Lanthanum Metal: Knight Shifts, Spin Relaxation Rates, and Quadrupole Coupling Constants,” Physical Review, Vol. 179, No. 1, 1969, pp. 359- 368.
- D. Tromans, “Elastic Anisotropy of HCP Metal Crystals and Polycrystals,” IJRRAS, Vol. 6, No. 4, 2011, pp. 462-183.