Spectral Analysis Review
Vol.02 No.03(2014), Article ID:48357,2 pages
10.4236/sar.2014.23023
Modeling and Simulation in Spectroscopic Study
Lin Huang
Institute of Chemical and Engineering Sciences, Agency for Science, Technology and Research, Singapore, Singapore
Email: huang_lin@ices.a-star.edu.sg
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 May 2014; revised 5 June 2014; accepted 2 July 2014
Dear Readers:
Modeling and simulation has been increasingly applied to spectroscopic study over the last decade. Modeling is the process of producing a model; a model is a representation of the construction and working of some system of interest. A model is similar to but simpler than the system it represents. One purpose of a model is to enable the analyst to predict the effect of changes. A simulation of a system is the operation of a model of the system. The model can be reconfigured and experimented with, usually, this is impossible, too expensive or impracticable to do in the system it represents. The operation of the model can be studied, and hence, properties concerning the behavior of the actual system or its subsystem can be inferred. In its broadest sense, simulation is a tool to evaluate the performance of a system, existing or being proposed, under different configuration of interest and over long periods of real time.
Through the following representative example of Raman and infrared spectroscopic study, let us look at how modeling and simulation plays an indispensable role in predicting and interpreting spectra of matters.
Spinel phases of lithium manganese oxides are important positive electrode and lithium-selective ion-sorption materials. Vibrational spectroscopy is a powerful tool to examine structural changes in these oxides [1], being sensitive to the short range environment of oxygen coordination around both manganese and lithium ions. In order to establish the relationship between the lattice structures and the vibrational spectra of lithium manganese oxides, there is a need of a fundamental understanding of the lattice vibrations, particularly those that are Raman and infrared active. Ammundsen et al. [2] used atomistic simulation methods based on an interatomic potential model to determine the normal modes of the zone-center (k = 0) lattice phonons in spinel LiMn2O4. They compared the results of these calculations with Raman and infrared experimental data of the LiMn2O4 bulk phase. Their simulation allowed the Raman and infrared spectra of spinel LiMn2O4 to be assignable.
By atomistic simulation [3]-[5], the calculations were carried out using energy minimization procedures embodied in the GULP (General Utility Lattice Program) code. The interatomic potentials are based on the Born model of the solid, which includes a long-range Coulombic interaction and a short-range term to model overlap repulsions and van der Waals forces. The electronic polarizability of the ions is described by the shell model, which is effective in simulating the dielectric and lattice dynamical properties of metal oxides.

The simulation of the LiMn2O4 oxide lattice was performed using two-body potentials for Mn-O, Li-O and O-O interatomic interactions. The shell model parameters were refined to achieve the best fit of predicted wave numbers of Raman and infrared active vibrations to experimentally observed ones. These potential and shell model parameters are given in Table 1. The calculated lattice parameters and atomic positions for LiMn2O4, after energy minimization to generate a relaxed equilibrium structure, are shown in Table 2. The data show excellent agreement with the experimentally observed structure (Table 2).
The calculated and observed wave numbers, symmetry species and optical activities of the lattice vibrations for LiMn2O4 are given in Table 3. The assumption made for this lattice is that cations and O anions are completely ordered. The number of lattice phonons and their symmetry species agree with factor group analyses for the primitive rhombohedral Bravail cells [6]. For LiMn2O4, there are 39 phonons distributed as:
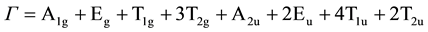
As shown in Table 3, the calculations predict five Raman active modes for LiMn2O4, one of A1g symmetries, one of Eg symmetries and three of T2g symmetries. The Mn ions are motionless for all of the eigenvectors. The A1g and Eg vibrations involve only oxide ion displacements. The T2g(2) and T2g(3) phonons are characterized by large oxygen motions and very small Li displacements, but the lowest energy T2g(1) phonon derives predominantly from a vibration of the Li sublattice.
The experimental Raman data for the LiMn2O4 bulk phase consist of a series of broad bands between 300 and 700 cm−1. The two T2g(1) and Eg modes which are calculated at 354 and 434 cm−1 are visible as weak features at 365 and 432 cm−1. The calculations assign the three strong bands at 480, 590 and 625 cm−1 to the T2g(2), T2g(3) and A1g phonons. The three bands correspond to the modes calculated at 455, 597 and 598 cm−1.
As seen in Table 3, the calculations predict that four vibrational modes will appear in the infrared spectrum of LiMn2O4. Two higher wave number modes at 517 and 633 cm−1 are attributed to T1u(3) and T1u(4), and two lower wave number modes at 287 and 383 cm−1 are ascribed to T1u(1) and T1u(2). Experimentally, the former
Table 1. Interatomic potentials for LiMn2O4.
aPotential cutoff = 12 Å.
Table 2. Calculated and experimental crystal properties for LiMn2O4.
Table 3. Calculated and observed vibrational spectral properties for LiMn2O4.
two modes are observed as intense broad bands at 513 and 615 cm−1, easily resolved in the mid-infrared region. The latter two modes at 287 and 383 cm−1 are discerned as a weak band at 277 cm−1 and a shoulder band at 360 cm−1, respectively.
Modeling and simulation is of significant importance in spectroscopic study. In the absence of single-crystal data, it is difficult to assign Raman spectroscopic bands of matters to modes of different symmetries. Although infrared spectra of matters have been reported in numerous studies, the interpretations have been mainly limited to empirical comparisons. There is considerable uncertainty in the assignment of bands observed, especially with complex spectra consisting of multiple bands and/or overlapping bands. Therefore, it is really necessary to predict spectroscopic bands of matters by group theory. There is a need of theoretical models to simulate and understand spectroscopic data of matters.
References
- Richardson, T.J., Wen, S.J., Strichel, K.A., Ross Jr., P.N. and Cairns, E.J. (1997) FTIR Spectroscopy of Metal Oxide Insertion Materials: Analysis of LixMn2O4 Spinel Electrodes. Materials Research Bulletin, 32, 609-618. http://dx.doi.org/10.1016/S0025-5408(97)00022-6
- Ammundscn, B., Burns, G.R., Islam, M.S., Kanoh, H. and Rozière, J. (1999) Lattice Dynamics and Vibrational Spectra of Lithium Manganese Oxides: A Computer Simulation and Spectroscopic Study. Journal of Physical Chemistry B, 103, 5175-5180. http://dx.doi.org/10.1021/jp984398l
- Catlow, C.R.A. (1987) Computational Techniques and Simulation of Crystal Structures. In: Cheetham, A.K. and Day, P., Eds., Solid State Chemistry Techniques, Chapter 7, Clarendon Press, Oxford.
- Gale, J.D. (1997) GULP (General Utility Lattice Program). Royal Institution of GB and Imperial College, London, 1991-1996.
- Gale, J.D. (1997) GULP: A Computer Program for the Symmetry-Adapted Simulation of Solids. Journal of the Chemical Society, Faraday Transactions, 93, 629-637. http://dx.doi.org/10.1039/a606455h
- White, W.B. and De Angelis, B.A. (1967) Interpretation of the Vibrational Spectra of Spinels. Spectrochimica Acta Part A: Molecular Spectroscopy, 23, 985-995. http://dx.doi.org/10.1016/0584-8539(67)80023-0


