World Journal of Engineering and Technology
Vol.03 No.04(2015), Article ID:60874,9 pages
10.4236/wjet.2015.34016
Parameters Optimization for Piezoelectric Harvesting Energy from Pavement Based on Taguchi’s Orthogonal Experiment Design
Chunhua Sun, Hongbing Wang, Guangqing Shang, Jianhong Du
Department of Mechanic and Electronic Engineering, Suzhou Vocational University, Suzhou, China

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 5 August 2015; accepted 31 October 2015; published 3 November 2015

ABSTRACT
To effectively harvest vibration energy from pavement without affecting driving comfort and safety, parameter optimization was done with the orthogonal experiment design and the finite element analysis. L16(44) Taguchi’s orthogonal experiments were carried out with planted depth, PZT material, PZT diameter and thickness as optimization parameters and with open voltage and pavement displacement as optimization objectives. The experiment results were obtained via the finite element method. By using range analysis method, the dominance degree of the influencing factors and the optimum condition was obtained for the two objectives, respectively. Further, the multi- objective optimization was performed based on a weight grade method. The combined optimum conditions in order of their dominance degree are PZT diameter 35 mm, PZT thickness 6 mm, planted depth 50 mm and material PZT4. The validity of optimization scheme was confirmed.
Keywords:
Piezoelectric Energy Harvesting, Pavement, Taguchi’s Orthogonal Experiment, Finite Element Method

1. Introduction
Piezoelectric harvesting energy from pavement is a new process of capturing the wasted pavement vibration and transferring it into electricity to store it for later use or to power electronic sensors [1] . Since the 1990s, the technology has attracted more and more attention because of its unique advantages such as high energy convert efficiency, simple piezoelectric device, and applicability for miniaturization [2] . Some studies have been carried out on the effect of cymbal piezoelectric transducers of structural parameters on potential electrical energy and coupling with pavement [3] . Electromechanical analysis of piezoelectric harvesting unit from road vibration was also done with the finite element method (FEM) [4] . The effect of traffic flow on characteristics of piezoelectric harvesting unit from pavement was analyzed [5] [6] . However, little application of the technology has been realized until now [7] . The main reason consists in the relative small current and low power compared to some other harvesting energy techniques such as electromagnetic and photovoltaic. Therefore, it is of significance for the practical application of piezoelectric energy harvesting to improve process efficiency through parameter optimization.
It has been well known that Taguchi’s approach is an efficient way to correlate various factors for parameter optimization and to identify the most influencing factors based on the experimental design and analysis method with good consistency and reproducibility. To our knowledge, the studies on the application of Taguchi experimental design for the purpose of high efficiency of piezoelectric harvesting energy are few [8] . And the application of the method to parameter optimization of piezoelectric harvesting device from pavement is not yet reported.
In this paper, the optimization of piezoelectric harvesting device from pavement was studied based on Taguchi experimental design for high efficiency of harvesting energy and good coupling with pavement. The parameters, including embedded depth, thickness and diameter of PZT disk, and material type of PZT disk, were involved. Firstly, the influence of factors on piezoelectric harvesting device from pavement was investigated. Then, the orthogonal experiments were carried out and analyzed with the output voltage and relative displacement ratio as optimization objectives. Dominance degree of the factors and the optimum conditions for piezoelectric harvesting energy from pavement were studied.
2. Optimization Objectives and Parameters
Figure 1 shows the harvester-pavement coupling system, on which a piezoelectric harvester is used to scavenge pavement vibration caused by vehicle traveling and transfer it into electricity. A successful harvester used in the system should have the abilities that it can convert mechanical energy into electrical power as more as possible and maintain the safety and comfort performance of the pavement. Thus, two basic performances are required for the harvester as following: 1) high efficiency of harvesting energy; 2) good coupling with pavement.
The efficiency of a harvester is always represented by the electromechanical coupling factor k and the energy transmission coefficient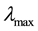 . However, it is difficult to calculate k and
. However, it is difficult to calculate k and 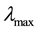 in the complicated harvester-pavement coupling system. Instead of them, the voltage at open circuit, which is directly related to the energy convert efficiency, is adopted to evaluate the energy harvesting ability in this paper.
in the complicated harvester-pavement coupling system. Instead of them, the voltage at open circuit, which is directly related to the energy convert efficiency, is adopted to evaluate the energy harvesting ability in this paper.
The output voltage of PZT disk under the applied stress can be obtained from the following equation in [9] :
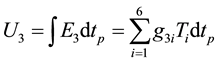 (1)
(1)
Figure 1. Harvester-pavement coupling system.
 (2)
(2)
where, 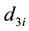 is piezoelectric strain constant tensor;
is piezoelectric strain constant tensor; 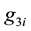 is the piezoelectric voltage constant of PZT;
is the piezoelectric voltage constant of PZT; 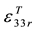 is the relative dielectric constant of PZT;
is the relative dielectric constant of PZT; 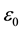 is the dielectric constant of vacuum;
is the dielectric constant of vacuum; 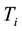 is the stress tensor;
is the stress tensor; 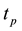 is thickness of PZT disk;
is thickness of PZT disk; 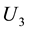 is the electric potential(the difference of the electric potential is referred as voltage) along the direction of 3 caused by polarization changing, which can be obtained via FEM.
is the electric potential(the difference of the electric potential is referred as voltage) along the direction of 3 caused by polarization changing, which can be obtained via FEM.
Meanwhile, the good coupling with pavement reflects that there is no much change of pavement displacement with or without the harvester under pavement while a vehicle passes through. Here, the relative deformation ratio p is adopted to express the coupling property.
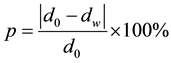 (3)
(3)
where, d0 and dw represent the pavement displacements without and with the harvester under the pavement, respectively.
If the relative deformation ratio p is less, it indicates that the harvester has good coupling with pavement. The pavement displacement d0 and dw can be obtained according to the maximum displacement value of the pavement via FEM. Therefore, the output voltage 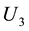 and the relative deformation ratio p are taken to be the optimization objectives.
and the relative deformation ratio p are taken to be the optimization objectives.
Parameters, which affect the harvesting energy efficiency and coupling with pavement, deal with three types. One is related to the harvester’s ceramic material, another relates to the harvester structure and the other is the embedded depth under pavement. If the cylindrical harvester is adopted in the harvester-pavement piezoelectric system, the structural parameters of the harvester include the diameter and thickness of PZT disk.Therefore, the detailed parameters including the embedded depth of the harvester under pavement, PZT material, the diameter and thickness of PZT disk, are chosen to optimize.
3. Parameter Optimization by Taguchi’s Orthogonal Experiment Design
3.1. The Taguchi’s Orthogonal Experiment Design
According to the Taguchi parameter design methodology, a 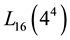 standard orthogonal array with four factors in four levels each in 16 runs is employed. The
standard orthogonal array with four factors in four levels each in 16 runs is employed. The 
The results of open voltage


The orthogonal experiment was analyzed by range analysis method for 
3.2. Single-Objective Optimization
In Table 2, the arithmetical parameter ki is the average value of the objective variable, where i denotes the level of the certain factor. R is the range calculated as the difference between the maximum and the minimum values of ki for a certain factor. According to the value of R, the dominance degree of each factor can be determined.
Table 3 shows the analysis results according to single objective of 

Experiments were run according to the chosen optimum conditions. The optimized values are shown in Figure 2. The voltage objective 
Table 1. Schedule and Results of Taguchi’s orthogonal experiments.
Table 2. Analysis of orthogonal experiments for two single objectives.
Table 3. Optimization result for two single objectives.

Figure 2. Comparison of experimental results and optimum conditions.
pared to the several highest values of the orthogonal experimental results in Table 1, as shown in Figure 2(a). The optimization objective of open voltage under the optimum conditions is higher than the results from the orthogonal experiment. While, in Figure 2(b), the relative deformation ratio p of 1.92% under the selected optimum conditions is listed in contrast to the smallest values of the orthogonal experimental results in Table 1. From this figure, the optimization objective of p under the optimum conditions is the smallest one compared to the ones in Table 1.
3.3. Multi-Objectives Optimization
Considering the practical application of harvester-pavement piezoelectric system, 

where 


The following discussion is on the multi-objectives optimization. Table 4 shows the range analysis of the orthogonal experiments for the objective variable, Y. The analysis results show that the optimum condition for the maximum value of Y in order of dominance degree is PZT thickness 6 mm, PZT diameter 35 mm, planted depth 50 mm and material PZT4. This is different from our above single-objective analysis results. It can be seen that the harvester structural parameters including diameter and thickness are the two most important factors for the overall objective while the PZT material has the most minor influence on it.
In the optimum conditions, the open voltage 
4. Effect of Each Factor on Objectives
4.1. Effect of Planted Depth
Figure 3 shows the effect of planted depth on open voltage 
Figure 3. Effect of Planted depth.
Table 4. Analysis for multi-objectives optimization.
tion ratio also increases with the planted depth except of 30 mm. It shows that the output voltage benefits from the bigger of the planted depth.
4.2. Effect of PZT Materials
The effect of different PZT materials on open voltage and relative deformation ratio is shown in Figure 4. It can be seen that the material of PZT4 can be harvested the maximum voltage and caused the minimum pavement deformation. The material of PZT5A also possesses better performance for harvesting pavement vibration with consideration of the harvested electricity and pavement deformation.
4.3. Effect of PZT Thickness
Figure 5 shows the effect of PZT thicknesses on open voltage and relative deformation ratio. The relative deformation ratio decreases with increasing thickness of PZT disks as shown in Figure 5. However, the open voltage shows a irregular trend.
4.4. Effect of PZT diameter
Figure 6 shows the effect of PZT diameters on open voltage and relative deformation ratio. From the figure, open voltage increases and relative deformation ratio decreases while PZT diameter increases. But both vary in nonlinearity.
5. Finite Element Analysis Model
In order to save manpower, material and financial resources, the finite element method was used in the paper to
Figure 4. Effect of PZT materials.
Figure 5. Effect of PZT thickness.
perform the electromechanical analysis. Figure 7 shows the finite element model via ANSYS. Here, only one tire load is considered because the size of the harvester is small comparing to the contact area. Provided that the diameter of tire load area is 213 mm and the contact stress is 0.7 MPa. The diameter of asphalt pavement is 1000 mm. The height of pavement is set to be 150 mm according to the standard structure of pavement.
The mesh of Plane 42, which is suitable for elastic material properties, is used for asphalt pavement and end cap. Mean while, Plane 13 is adopted to mesh the piezoelectric material. The material properties can be found in [10] . The simulation results are filled in Table 1 based on the parameter combination of the orthogonal experimental design.
6. Conclusion
To optimize the harvester parameters and the embedded position in piezoelectric harvesting from pavement vi-
bration, 
Figure 6. Effect of PZT diameter.
Figure 7. Finite element model.
planted depth, PZT material, PZT thickness and diameter as optimization parameters. The finite element method was adopted to do experiment. It is demonstrated that the open voltage varies in wide range and the relative deformation ratio has less change under the conditions in orthogonal experiment design. Range analysis results show that the planted depth is the most important factor for open voltage while it is not so important for relative deformation ratio. The PZT diameter and thickness are the key important factors for all the two optimization objectives. Different PZT materials have fewer influences on two objectives. By using the weight grade method, the optimum conditions obtained from the two-objectives optimization are PZT thickness 6 mm, PZT diameter 35 mm, planted depth 50 mm and PZT4 material, which are in order of their dominance degrees. The validity of the optimum conditions is confirmed and is of practical value for the application of piezoelectric energy harvesting technology in pavement.
Acknowledgements
This research was supported by the National Natural Science Foundation of China (No. 51175359) and the 4th “333 Engineering” Research Funding Project of Jiangsu Province (BRA2014086).
Cite this paper
ChunhuaSun,HongbingWang,GuangqingShang,JianhongDu, (2015) Parameters Optimization for Piezoelectric Harvesting Energy from Pavement Based on Taguchi’s Orthogonal Experiment Design. World Journal of Engineering and Technology,03,149-157. doi: 10.4236/wjet.2015.34016
References
- 1. Huang, R.-B., Niu, Y.-L., Zhao, H.-D. and Chang, H.-B. (2012) Technical Approach and Research Prospect of Piezoelectric Energy Harvest from Highway. China Journal of Highway and Transport, 25, 1-8. (In Chinese)
- 2. Priya, S. and Inman, D.J. (2009) Energy Harvesting Technologies. Springer, New York.
http://dx.doi.org/10.1007/978-0-387-76464-1 - 3. Zhao, H.D., Yu, J. and Ling, J.M. (2010) Finite Element Analysis of Cymbal Piezoelectric Transducers for Harvesting Energy from Asphalt Pavement. Journal of the Ceramic Society of Japan, 118, 909-915.
http://dx.doi.org/10.2109/jcersj2.118.909 - 4. Sun, C.-H., Zhang, Y.-K., Du, J.-H. and Shang, G.-Q. (2013) Electromechanical Analysis of Piezoelectric Harvesting Unit from Road Vibration with FEA. Advanced Materials Research, 726-731, 3144-3147.
- 5. Lee, J., Lee, M., OH, J., et al. (2010) Study on the Energy Conversion from the Dynamic Load of Vehicles on the Road Using Piezoelectric Material. Materials Science Forum, 658, 57-60.
http://dx.doi.org/10.4028/www.scientific.net/MSF.658.57 - 6. Sun, C.-H. and Shang, G.-Q. (2014) Effect of Traffic Flow on Characteristics of Piezoelectric Harvesting Unit. Applied Mechanics and Materials, 672-674, 902-905.
http://dx.doi.org/10.4028/www.scientific.net/AMM.672-674.902 - 7. Innowattech Ltd. (2008) Innowattech’s Solution—The Innowattech Piezo Electric Generator (IPEG™) [EB/OL].
- 8. Wu, S.-L., Zhang, Q. and Huang, Z.P. (2010) Optimization of Resonance Frequency of Spherical-Cymbal Transducer Based on Orthogonal Experiment. Chinese Journal of Scientific Instrument, 31, 683-691.
- 9. Vives, A.A. (2008) Piezoelectric Transducers and Applications. 2nd Edition, Springer, New York.
http://dx.doi.org/10.1007/978-3-540-77508-9 - 10. Zhao, X.M. (2006) Experimental Design Methods. Science Press, Beijing. (In Chinese)








