Received 21 January 2015; accepted 3 April 2015; published 7 April 2015

ABSTRACT

Continuous Stirred Tank Reactors (CSTR) are used ubiquitously in chemical process industry for mixing, reactions and crystallizations. The purpose of this research is to study the effect of solute concentration (sodium chloride) on the stirrer speed in a CSTR. The experimental method used in this research is the stop watch and beaker method. The behavior pattern of the fluid in a CSTR can be experimentally verified as an alternative to the mathematical model. The tracer experiments were carried out. The effect of different parameters such as stirring speed, concentration at a steady time interval was analyzed. Experimental data obtained at 0.6 M and 160 rpm gave a curve that is in close agreement to that of theoretical or mathematical model. In other words, the results obtained at a concentration of 0.6 M and 160 rpm are in close agreement with that of early re- searchers. The paper is divided into five main sections: the first section immediately after the abstract is the introductory section that is basically a review of literature; the second section takes care of the materials and methods; the third section is the experimental procedure and this sec- tion takes the shut-down procedure and data processing into consideration; the fourth section is the discussion of experimental results and the last section is the conclusion of the paper.

Keywords:

Continuous Stirred Tank Reactor (CSTR), Residence Time Distribution (RTD), Revolution per Minutes (RPM)

1. Introduction

“Tracer” or Residence time distribution (RTD) studies are commonly exploited as a means of developing an understanding of the “mixing” status of vessels of various types. Continuous Stirred Tank Reactors have been the focus of various Residence Time Distribution studies over the years. Experiments carried out by Bakker et al. (2001), Berty (1999), Choi et al. (2004), Fogler (2006), Bancroft et al. (2003), and Josh et al. (2008) for Continuous Stirred Tank Reactors of standard size (diameter equals height) with standard baffle designs and various impeller designs have been done for a broad range of tank sizes, feed flow rates, and impeller revolutions per minute [1] -[6] .

In developing a mathematical model to predict the ideal transient concentration in a continuous stirred tank reactor (CSTR) using the tracer experiments, the residence time distribution (RTD) is created and compared to the ideal RTD for a continuous stirred tank reactor [7] .

Continuous stirred tanks are used ubiquitously in the chemical process industry for mixing, reactions, and crystallizations. The mixing in a continuous stirred tank is often not ideal. The residence time distribution (RTD) is one of the ways to characterize the non-ideal mixing in the tank. Comparison of the measured RTD with that of an ideal reactor allows the process engineer to diagnose the ills of the tank and mixer design. The engineer can then use an appropriate mixing model for the tank in combination with the kinetics of the reaction to be performed in the tank to develop an appropriate model for the reactor [8] .

The residence-time distribution (RTD) of a reactor is a characteristic of the mixing that occurs in the chemical reactor. There is no axial mixing in a plug-flow reactor. And this omission is reflected in the RTD. The CSTR is thoroughly mixed and possesses a far different kind of RTD than the plug-flow reactor [9] .

Nevertheless, the RTD exhibited by a given reactor yields distinctive clues to the type of mixing occurring within the reactor which is one of the most informative characterizations of the reactor [4] .

Nonreactive substances that can be used in small concentrations and that can easily be detected by analysis are the most useful tracers. When making a test, tracer is injected at the inlet of the vessel along with the normal charge of process or carrier fluid, according to some definite time sequence. The progress of both the inlet and outlet concentrations with time is noted. Those data are converted to a residence time distribution (RTD) that tells how much time each fraction of the charge spends in the vessel [7] .

A RTD, however, does not represent the mixing behaviour in a vessel uniquely, because several arrangements of the internals of a vessel may give the same tracer response, for example, any series arrangements of reactor elements such as plug flow or complete mixing. This is a consequence of the fact that tracer behaviour is re- presented by linear differential equations. The lack of uniqueness limits direct application of tracer studies to first-order reactions with constant specific rates. For other reactions, the tracer curve may determine the upper and lower limits of reactor performance. When this range is not too broad, the result can be useful. Tracer data also may be taken at several representative positions in the vessel in order to develop a realistic model of the reactor [10] .

In order to analyze the residence time distribution of the fluid in a reactor the following relationships have been developed. Fluid elements may require differing lengths of time to travel through the reactor. The distribution of the exit times, defined as the E(t) curve, is the residence time distribution (RTD) of the fluid. The exit concentration of a tracer species C(t) can be used to define E(t) [8] .

Deviation from the two ideal flow patterns can be caused by channelling of fluid, by recycling of fluid, or by creation of stagnant regions in the vessel. In all types of process equipment, such as heat exchangers, packed columns, and reactors, this type of flow should be avoided since it always lowers the performance of the unit [9] .

If it can be known precisely what is happening within the vessel, if one has a complete velocity distribution map for the fluid in the vessel, then one should, in principle, be able to predict the behaviour of a vessel as a reactor. Unfortunately, this approach is impractical, even in today’s computer age [4] .

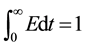(1.1)

This procedure is called normalizing the distribution.

Nonreactive substances that can be used in small concentrations and that can easily be detected by analysis are the most useful tracers. When making a test, tracer is injected at the inlet of the vessel along with the normal charge of process or carrier fluid, according to some definite time sequence. The progress of both the inlet and outlet concentrations with time is noted. Those data are converted to a residence time distribution (RTD) that tells how much time each fraction of the charge spends in the vessel [7] , as shown in Figure 1.

Mathematically differential equations and their solutions will be stated for the elementary models with the

main kinds of inputs. Since the ODEs are linear, solutions by Laplace transforms are feasible.

With a step input of magnitude 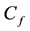the unsteady material balance is

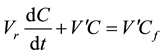(1.2)

Whose integral is

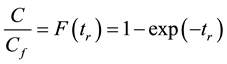(1.3)

With an impulse input of magnitude m or an initial mean concentration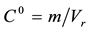, the material balance is

(1.4)

And

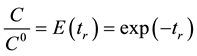(1.5)

From these results it is clear that

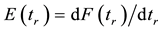(1.6)

Since a tracer material balance is represented by a linear differential equation, the response to any one kind of input is derivable from some other known input, either analytically or numerically. Although in practice some arbitrary variation of input concentration with time may be employed [11] .

2. Materials and Methods

The RTD is determined experimentally by injecting a 5 ml volume of inert chemical tracer (a 10% methyl blue dye) into the tank which contains standard solutions of NaCl at time zero. In all experiments, the feed tube was the inlet pipe. Analyzers detected each of the species in the tracer; blue dye with the aid of a video camera, temperature with a thermometer, salt with conductivity meter, and concentration with pH meter were measured simultaneously at definite experimental conditions such as time and mixer rpm values.

Great care was used in synchronizing the pulse input with the initiation of data accumulation for RTD analysis and to calibrate the geared motor to ensure that the reactor space-time was accurately measured. For all of these experiments, data were taken at 20-s intervals.

All of these measurements were used to monitor the concentration of the tracer inside and exiting the reactor. The calibration of the experimental set-up was done before each run to ensure measurement accuracy. The RTD measured was the combination of process dynamics and sensor dynamics.

The experimental set-up is as shown in Figure 2.

3. Experimental Procedure

1) The conductivity meter was calibrated.

A) Aqueous sodium chloride solution was made using graduated cylinder, at 0.2 M, 0.4 M and 0.6 M concentration.

B) The conductivity meter probe was inserted into the solution. Efforts were made to avoid probe contact with walls or bottom of container.

C) The CAL. Button on the meter was pressed so as to create a reference standard.

D) This was scrolled to factory calibration settings and the “enter” button was pressed.

E) Process A to D was repeated for multiple standard solutions.

2) The tank was filled with known amount of solution.

3) The impeller was set to desired speed.

4) The solution was allowed to mix thoroughly.

5) The sample collection beaker was placed under the reactor exit nozzle.

6) The beaker and stopwatch method was used to record conductivity measurements with respect to time using constant time intervals. To operate the conductivity meter:

A) The probe was placed into the sample, immersing the slot on the end of the probe.

B) The probe was shaken for five to ten seconds to remove bubbles.

C) The COND. Button was pressed to calculate conductivity.

D) A record of conductivity and time values was taken.

E) The concentration versus conductivity plot was used to record concentration values

7) The experiment was stopped once the conductivity values flat line near water conductivity value

8) After a complete run, the tank was thoroughly cleaned to remove any excess salt residue.

9) Repeated steps 2 - 9 for additional impeller speeds.

10) Repeated steps 1 - 10 for additional sodium chloride solutions.

3.1. Shutdown Procedure

1) Turn the CSTR impeller speed setting to 0 RPM.

2) Turn OFF the CSTR ON/OFF switch.

3) Close the water control valve.

4) Turn OFF the motor control Switch

5) Turn OFF the mains control Switch.

3.2. Data Processing

In order to establish the ideal RTD, concentration curve, and E(t) curve, Equations (1.4) and (1.12) are evaluated and plotted as a function of time. 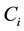is identified by adding a known quantity of NaCl tracer to the reactor. V is identified by adding a known amount of water into the reactor tank and Q is identified by the stop watch and beaker method. Once the base line was established, the experimental concentration curves are created by taking effluent samples from the outlet at known times and measuring NaCl conductivity. Again Equation (1.4) and (1.5) are utilized to produce concentration curves with respect to time. Each set of data for a particular sodium chloride solution is compared to the ideal curve.

4. Discussions

“Tracer” or Residence time distribution (RTD) studies are commonly exploited as a means of developing an understanding of the “mixing” status of vessels of various types. Continuous Stirred Tank Reactors have been the focus of various Residence Time Distribution studies over the years. Experiments carried out by Andre et al. (2001), Berty (1999), Byung et al. (2004), Gregory (2003), Hamit et al. (2008), and Marina and Alfredo (2004) for Continuous Stirred Tank Reactors of standard size (diameter equals height) with standard baffle designs and various impeller designs have been done for a broad range of tank sizes, feed flow rates, and impeller revolutions per minute [1] -[6] .

In performing the tracer test experiments, standard solutions of NaCl were prepared in 0.2 M, 0.4 M and 0.6 M with methyl blue as the tracer. 0.2 M, 0.4 M, and 0.6 M solutions at 80 rpm, 100 rpm, 120 rpm, 140 rpm and 160 rpm, at 20 seconds intervals. Twenty eight number of value were taken for each rpm and each concentration, thus, generating a total number of twenty five curve plots for each 20 seconds interval at a particular rpm (600 second in total).

From Figure 3, the solution shows a fast exponential rate of reduction with increase in time, the exponential reduction rate is almost as that of the ideal between the 280 seconds and 480 seconds, however, from the 520 seconds, the exponential reduction was tending to zero.

From Figure 4, at the speed of 100 rpm, the rate of decrease was not steady, for the first 100 seconds, the exponential rate of decrease was steady; however, between the 120 seconds and the 420 seconds, an unexplainable behavior was observed, at the 330 seconds, the values tended toward infinity.

Figure 5 and Figure 6 show no considerable difference from Figure 4. However, Figure 7 at 160 rpm shows a behaviour pattern that tends toward the ideal.

Figure 8 shows an exponential decrease in concentration with time that is quite far from the ideal. Figure 9 and Figure 10 show steady graduation towards ideal. Figure 11 and Figure 12 show a complete deviation from the ideal. These deviations could be due to improper mixing of the NaCl particles with the solvent.

From Figure 12 to Figure 16, at 80 rpm, 100 rpm, 120 rpm, 140 rpm, respectively, the exponential decrease behavior patterns are quite very similar to the ideal, however, at 160 rpm, the pattern is very similar to the ideal, as shown in Figure 17. Thus, the analogy that the optimum molarity for characterization of the CSTR fabricated

is 0.6 M NaCl and the optimum rpm is 160.

From Figures 18-32, it could be observed that there is a similar pattern of the curves behavior of the resi-

dence time distribution to that of the concentration gradient. It is important to state that Figure 32 shows a similar trend of curve that is quite as same as the ideal. With these findings, it can be stated that the RTD curve at 0.6 M of NaCl at 160 rpm gives the optimum result.

5. Conclusions

In conclusion, it can be said that the purpose of this research work was extensively achieved in that, the CSTR used for this experiment gave a curve pattern in close agreement to that of the ideal at 0.6 M concentration of NaCl at 160 rpm which compares favourably with that in established text and similar research work carried out by earlier researchers.

Second, it can be said that the result obtained verifies the theory that the stop watch and beaker method can experimentally validate the mathematical model method in verifying the behavior of CSTR.

References