ABSTRACT

It is important to understand the mechanism and implications of different modifiers on analytical and preparative processes under chromatography with supercritical fluids (SFs) and under extraction with SFs. Supercritical fluid chromatography (SFC) and supercritical fluid extraction are generally carried out with neat supercritical carbon dioxide (SCCO₂) or with SCCO₂ containing modifiers (or cosolvents), especially for strongly polar compounds. For example, methanol is added as a cosolvent/modifier to SCCO₂ for the extraction/separation of polar compounds. This paper discusses the influence of the modifier on the colligative properties of the principal mobile phase, which may define the situation in the total mobile phase in a chromatography column or in parts of a column under SFC. No colligative behavior of solutions reflects individual properties of the solutes. Their cross-interactions with solvents are discussed.

Keywords:

Supercritical Fluid (SF), Supercritical Fluid Chromatography (SFC), Supercritical Fluid Extraction (SFE), Modifiers, Influence of Modifiers, Colligative Properties, Thermodynamics-Based Evaluation of Binary Mixtures, Phase Equilibria

1. Introduction

There are two main components of supercritical fluid chromatography (SFC) instrumentation: a capillary column supercritical fluid chromatograph, derived from a gas chromatograph instrument, and a packed column supercritical fluid chromatograph, derived from a high-performance liquid chromatograph instrument [1] [2] [3] . The mobile phase is delivered to the instrumentation used for capillary column supercritical fluid chromatography (CCSFC) as an unmodified or a modified supercritical fluid (SF) directly from a storage cylinder. CCSFC is, however, very seldom used. The focus of this paper is on packed column supercritical fluid chromatography (PCSFC), and we discuss its theoretical background.

The literature describes the reasons for failures in the construction of capillary column supercritical fluid chromatographs and CCSFC procedures, which make use of delivery from a single cylinder with premixed supercritical carbon dioxide (SCCO₂) and a modifier (methanol or formic acid) [4] . Several PCSFC concepts and procedures in which the modifier is mixed with SCCO₂ by a server pump in the mixer chamber are also described. Comprehensive reviews of the development and use of SFC techniques, methods, and instrumentation are presented [1] - [10] .

SFC is a very promising analytical tool for demanding separations of complex mixtures and isomers [1] [3] [5] - [10] . However, both the hardware, such as instrumentation and columns, and the theoretical basis are underdeveloped, in comparison with high-performance liquid chromatography (HPLC) and gas chromatography. A somewhat better situation exists for supercritical fluid extraction (SFE) [11] . The most attractive technique is PCSFC, largely due to the several advantages it offers: a wide range of detectors may be used [5] [10] , it is possible to use pressure programming and temperature programming, and there is a wide choice of modifiers available, in isocratic and programmed modes, for altering the composition of the mobile phase, pressure, and temperature. Using PCSFC, it is possible to perform semipreparative and preparative fractionation; this possibility is very limited, or impossible, with CCSFC.

The most attractive and frequently employed substance for SFE, as well as for SFC, is CO₂ in its supercritical state. SCCO₂ possesses favorable properties: it is noncorrosive, nonflammable, nontoxic, and environmentally friendly.

Some other inorganic candidates that may be employed, but are seldom used as principal mobile phases in a supercritical state, are xenon (Xe), nitrous oxide (N₂O), sulfur hexafluoride (SF₆), ammonia (NH₃), water (H₂O), and freons. Alkanes, such as ethane (C₂H₆), propane (C₃H₈), and n-butane (C₄H₁₀) have also been used, but they are highly flammable, making them the least preferred candidates for mobile phases.

Physicochemical properties and characteristics of polar and nonpolar SFs that may be used in SFE and SFC technologies are presented in the Table 1 (reproduced from [12] ).

1.1. Carbon Dioxide as the Principal Mobile Phase for SF Technologies

Figure 1 presents the phase diagram for pressure-temperature relations (bar/ Kelvin, K) for neat CO₂, with its triple and critical points. Built on thermophysical data from the NIST databases [13] [14] , Figure 1 develops the idea of ex-

Many other substances also can be used http://www.supercriticalfluid.org/Supercritical-fluids.146.0.html.

tending the saturation line to the SF zone, where a soft structural transition from the gas-like SF to the liquid-like SF takes place at a fluid density close to the critical density D_c [15] [16] . This extension is known as the Widom line. The equation for sublimation vapor pressure is taken from the NIST database [14] .

The phase diagrams indicate the conditions for triple and critical points; the regions for the existence of vapor, liquid, condensing, melting, freezing, existence of solid, deposit, and sublimation; and the lines of sublimation, melting, and saturation. The important conditions for the critical point and the extension of the saturation line to the SF zone are also evident.

The influence of modifiers on phase diagrams for pressure-temperature relations and the triple and boiling points, and lines of solid, liquid, and vapor separation will be demonstrated later.

1.2. The Role of Modifiers to CO₂ in SF Technologies

Neat CO₂ in a supercritical state is primarily employed for the extraction of hydrophobic molecules and, at best, it can dissolve some moderately polar compounds. CO₂ alone is very seldom used. This is because neat CO₂ is rather lipophilic and polar/strong polar substances do not dissolve well in it. This issue can be resolved to some extent by elevation of pressure or modification of temperature, or both [3] . In addition to altering the pressure and temperature of neat CO₂, modifiers or cosolvents―which are polar in nature, such as water, methanol, ethanol, diethylamine, formic acid, acetic acid, and many other polar and even nonpolar solvents, and complexation agents―are added to SCCO₂ to enhance bond separation and the extraction of strongly polar compounds and ions. By using one component as modifier, or a mixture of different substances as modifiers, it is possible to achieve a wide range of analyte solubilities in the mobile phase of modified SCCO₂. Methanol and ethanol are often used as modifiers in SFC to enhance mobile phase polarity. Small m/z ions from these modifiers often do not disturb the fragmentation picture of large molecules under SFC- mass spectrometry (MS).

Methanol is an important modifier for SCCO₂ to achieve some polarity in this mobile phase [17] . However, ethanol is less toxic for the operator and the environment; it has been used in up to 30% molar volume in isocratic mode [18] . The practical experiments and data described in [19] are considered very important because of the large volumes of ethanol used as modifier. Multicomponent mixtures of CO₂, ethanol, and diethylamine, described in [18] , are not unique. Many complicated multicomponent mixtures of CO₂ with modifiers [17] , cosolvents, and even complexation agents are in use [11] .

Calculation of phase equilibria for multicomponent mixtures as described by Gernert et al. [20] can be very helpful for understanding the processes in SFC columns during bond separation in complex mixtures or the resolution of isomers. In section of columns under separation together with complex mobile phase also present analytes of different nature (which are present in initial analyzing mixture). Chueh and Prausnitz [21] [22] have modeled CO₂ with mixtures of some of these compounds (including methanol and ethanol) for the estimation of the critical parameters T_c and P_c. The most complete collection of SCCO₂ solubility data with multiple solutes is presented in “Solubility in Supercritical Carbon Dioxide” by Ram B. Gupta and Jae-Jin Shim [23] .

In some cases, polar supercritical phases have been used for chromatography and extraction and have advantages over CO₂ in the supercritical state [24] . This provides quantitative recovery and the possibility to overcome the matrix-ana- lyte interaction, which sometimes may be more important than a high solubility of the analyte in the solvent [24] . Polar supercritical principal phases, such as ammonia, can be used for the extraction of metal ions or polar substances from matrices by SFE or SFC [25] . Many salts and substances are readily soluble in ammonia in the supercritical state and this principal phase can also be modified to lend the principal mobile phase some lipophilic characteristics [25] . The pressure-temperature diagram for ammonia is presented in Figure 2, built on thermophysical data from the NIST databases [13] and [14] .

In several cases, ammonia in the supercritical state has advantages because it is polar, in contrast to CO₂ containing polar modifiers for the extraction of strongly polar compounds. This is because the addition of polar modifiers to CO₂ results in alteration of the critical temperature and critical pressure. Hence, the integrity of the supercritical phase should be carefully preserved by choosing

appropriate experimental pressures and temperatures. However, ammonia is extremely corrosive and toxic, which makes it the least preferred mobile phase.

1.3. Phase Transformations in SFC Columns

The mobile phase in a chromatography column under SFC is not homogeneous, even when using neat CO₂, because of a pressure gradient fall from the head of the column to the bottom (outlet). However, modern SFC instrumentation is equipped with a backpressure regulator (BPR) that can automatically hold a constant pressure at the outlet of the column in programmed mode, and hence define the pressure at the head of the column. The main purpose of a BPR is to prevent the conversion of SCCO₂ to CO₂ gas at the outlet of the column as well as to prevent freezing at the outlet as a result of this, i.e., the analyte is kept in the mobile phase in the supercritical state until it arrives in the detector.

In real situations, the following are often present in a column: in the head section of the column, the CO₂ mobile phase in a liquid state (depending on conditions); in the middle of the column, a section of SCCO₂; while at the bottom of the column, there is the section where CO₂ often exists as condensed gas under a high pressure (as a fluid under subcritical conditions). Of course, the operator can achieve better conditions by using an isocratic mode of operation with only two different phases: liquid in the head section of the column and SF in the main part of the column. However, this is not achievable with a programmed mode of operation of conditions and parameters, such as programmed pressure, programmed temperature, and programmed concentration of modifier in the mobile phase, simultaneously.

1.4. Use of Cosolvents/Modifiers in SFE

The solvating power of a SF at a given temperature depends on its density. The solubility of a solute in SCCO₂ depends on the intermolecular interactions between solvent and solute. The solvating power of SCCO₂ can be defined in terms of the solubility parameter, δ. It is defined as the square root of the cohesive energy density and is used extensively in interpreting the thermodynamic properties of a solution. It is given as follows:

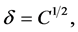
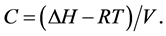
where ΔH is the heat of vaporization, V is the molar volume of the liquid, and С is the cohesive energy density.

For a SF, the heat of vaporization is zero at the critical temperature; therefore, the above equation leads to a negative value of С. The equation was later modified and Giddings proposed an equation based on studies in liquid chromatography using the van der Waals equation of state. The δ for a SFC is given as follows:

where ρ_r is the reduced density of the substance in supercritical state and ρ_r,liq is the reduced density of the liquid at its normal boiling point.

Thus, the solubility parameter for a given substance can be obtained if the fluid density and critical pressure are known, and it is unique for a given substance. When the solubility parameters of both the solute and solvent are similar, appreciable solubility of the solute will generally be observed in the given solvent. The solubility parameters of some SFs are given.

CO₂ in supercritical state is a nonpolar medium and it finds wide application in the extraction of organic compounds, such as natural products, which are generally hydrophobic in nature. SCCO₂ with the addition of modifiers/cosol- vents, such as methanol, is used for extraction of polar compounds. SFE of metal ions can be performed by adding suitable chelating agents to the SCCO₂ medium.

Modifiers or cosolvents are the substances that are added to SFs to alter solvent properties, i.e., to increase the polarity, aromaticity, chirality and the ability to complex various metal ions. For example, methanol or ethanol is added to CO₂ to increase polarity; toluene to impart aromaticity and neutral extractant; tri-n-butyl phosphate, dialkylalkyl phosphonates, dibutylbutyl phosphonate, and

diamylamyl phosphonate for solvation of metal complexes [11] . Addition of polar cosolvents may be effective in solubilizing the polar solute molecules. The modified CO₂ solvent may also absorb on the active sites of the matrix and prevent the readsorption of the analyte, and thereby its transfer to the supercritical phase. When modifiers are added to SFs, it is essential to evaluate the phase equilibria of the mixture and chemical interactions between them. Issues relating to estimation of the critical parameters for the mixtures should be carefully evaluated. At the critical point, the composition and density of the two phases become identical, and only one SF phase exists. For a given mixture at a given temperature, there will be a critical pressure and critical composition value.

Knowledge about the modifier-fluid phase diagram is essential to ensure that the solvent is in a single phase. For binary mixtures with a low interaction between components, the critical constants are approximately the arithmetic means of the T_C and P_C.

Here x_A and x_B are the molar shares of components A and B in the mixture. T_A and T_B are the critical temperatures and P_A and P_B are the critical pressures of components A and B, respectively.

In some mixtures, the cosolvent can interact with CO₂ and the resultant T_C and P_C may differ from the values based on a linear combination of the components T_C and P_C. Brunner et al. [26] estimated the critical parameters for the methanol-CO₂ system. CO₂ containing methanol can be taken to critical point only above a certain temperature, depending upon the composition of methanol in the CO₂ phase. For the methanol-CO₂ system at the CO₂ molar share equal to 0.84, the critical temperature is 50˚C and the critical pressure is 95.5 bar. However, linear estimation for the critical temperature of the above mixture is around 64˚C and linear estimation for the critical pressure is around 75 bar.

Because direct extraction of ionic species is inefficient in a neat SCCO₂ medium, chelating agents are generally added to a SCCO₂ medium to form neutral complexes. The latter are quite soluble in supercritical medium. A variety of chelating agents such as organophosphorous compounds, dithiocarbamates, and macrocyclic ligands have been used for the extraction of metal ions such as lanthanides, actinides, and transition metal ions [27] - [34] . Tributylphosphine (TBP) and trioctylphosphine oxide (TOPO) are some of the solvating extractants used in the SFE of actinides. Crown ethers are used for selective extraction of alkali/alkaline earth metal ions. The solubility of metal complexes in SFC medium is an important criterion for designing an efficient metal extraction process. In general, many chelating agents show relatively high solubility in SCCO₂. The β-diketones and fluorinated diketones have been used in SCCO₂ medium for the SFE of lanthanides and actinides. The extraction efficiency depends on the solubility of ligands as well as that of metal complexes in the supercritical medium.

In some cases, SCCO₂ will be delivered to an extraction vessel containing the ligand. The SCCO₂ stream containing the ligand is subsequently passed through another vessel containing the analyte (metal ion of interest). On some occasions, ligand is dissolved in methanol medium and mixed into SCCO₂ and the modified stream will be employed for metal ion extraction.

2. Colligative Properties of CO₂ with Modifiers

Colligative properties, such as vapor pressure depression, boiling point elevation, melting/freezing point depression, and osmotic pressure have played a decisive role in analytical chemistry prior to the discovery of chromatography and MS for identification of purity as well as for the determination of the molecular weight of substances. Use of the melting/freezing point depression of camphor or benzene was nearly a standard test for determining the molecular weight of an unknown substance.

Colligative properties depend only on the molar share y of the solute in solution, not on the nature of the solute. The molecular weight of the unknown nonvolatile substance is calculated from melting/freezing point depression ΔT_f using the following formula:

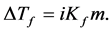(1)

where K_f is the cryoscopic constant, ΔT_f is the melting temperature depression, and m is the molality.

Van’t Hoff factor i is the number of particles that may arise from one solute molecule at its possible dissociation. In a nonpolar liquid or SCCO₂, there are no conditions for dissociation of solute molecules, and the van’t Hoff factor i = 1. The molality m is the number of moles of solute in 1 kg of a solvent [35] :

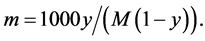(2)

where M is the gram molecular weight of the solvent and y is the molar share of solute. From Equations (1) and (2), we can determine the cryoscopic constant K_f:

(3)

At low values of y, the Equation (3) takes a more simple form: .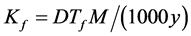

For a solution of a nonvolatile solute with molar share y, Raoult’s law [35] gives us the vapor pressure of solvent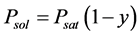, where P_sat is the vapor pressure of pure solvent. The triple point temperature depression results from derivations of P_subl(T) and P_sat(T):

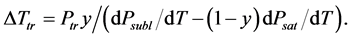(4)

where P_tr is the triple point vapor pressure, and P_subl(T) and P_sat(T) are vapor pressures along the sublimation and saturation lines, respectively. Equation (4) may be rewritten as:

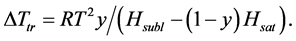(5)

where H_subl and H_sat are sublimation and saturation enthalpies for solid and liquid solvent.

Upon adding a substance (of another nature) to a pure solvent, we will achieve new properties, such as the melting, boiling, vaporization, condensing, freezing, triple, and critical points for this mixture, in comparison with the properties of the initial pure solvent. In the case of CO₂ in the supercritical state, upon adding the analyte as modifier we obtain a new pressure-temperature diagram (bar/ Kelvin, K) in modified CO₂. However, CO₂ differs from other solvents due to the high value of its triple point pressure, precluding the standard determination of melting and boiling points.

Despite an extensive search of the literature for the crucial parameters for the calculation of a new diagram of pressure-temperature relations for modified CO₂, we have not yet found the cryoscopic constant K_f for CO₂, because the triple point pressure in CO₂ is much above 1 bar. For this reason, we decided to use qualitative changes only as a model for understanding changes. When a nonvolatile solute is added to a solvent, the resulting solution has a vapor pressure P_sol(T) that is lower than the pure solvent saturation pressure P_sat(T), in accordance with the laws of Raoult and Dalton [35] .

The diagram for qualitative changes in pressure?temperature relations in CO₂ with a nonvolatile and nondissociating modifier at molar share y = 0.1 is presented in Figure 3, built on experimental data from the NIST databases [13] and [14] .

Bearing in mind that in pure CO₂ the triple point pressure P_tr = 5.185 bar, we had to take (in this unusual case) the value of pressure P_b for the estimation of melting and boiling points 10 times higher than the normal pressure. Hence, we investigated the CO₂ boiling point at an elevated pressure P_b = 10 bar. Figure 3 shows that in this case the depression of the melting point ΔT_f is almost the same as the ΔT_tr at 3.1 K. Estimation of the ΔT_tr, based on Equation (4), almost coincides with this value.

Equation (3) gives us an estimation for the cryoscopic constant in CO₂, K_f =

1.23 K kg/mol. This value is low, compared with other known solvents, and is much smaller than the K_f for water, which is 1.853 k・kg/mol. This may be explained by a large difference between H_subl and H_sat in CO₂ near the triple point. Elevated bond energy between CO₂ molecules in the solid phase prevents from melting up to high enough T_tr temperature. For this reason, the ratio of triple point temperature to critical temperature T_tr/T_cr = 0.712 is uniquely large for CO₂ compared with other substances. This large T_tr/T_cr ratio also explains the uniquely large P_tr value for CO₂.

To estimate the increase in boiling temperature in a 0.1 M solution, we built the saturated vapor pressure P_sat(T) dependence for pure CO₂ (solid blue line in Figure 3, based on data from [13] ), and the partial CO₂ vapor pressure P_y(T) over a 0.1 M solution (dashed blue line), which according to Raoult’s law is equal to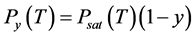. We found temperature T_sat, corresponding to pure CO₂ at pressure 10 bar, and T_y, corresponding to 0.1 M solution at the same pressure: T_sat = 233.03 K and T_y = 235.96 K. The difference is the boiling temperature elevation ΔT_b = 2.93 K.

The ebullioscopic constant may be calculated from the boiling temperature elevation ΔT_b using a formula, similar to Equation (3): Figure 3 and P_sat(T) dependence give an estimation for the boiling temperature ΔT_b elevation in CO₂ for 0.1 M solution at boiling pressure P_b = 10 bar, ΔT_b = 2.93 K. This results in K_b = 1.16 kg/mol. This value is close to K_b = 1.19 K kg/mol for ethanol, but was found at 10 times higher pressure.

3. Solubility of Polar Modifiers in Dense Gaseous Solvents

In studying polar modifiers, such as water, methanol, or ethanol, added to solvents, as used in SF technologies, we start from dense gaseous solutions. The dimension of solubility is mol/mol: the number of solute moles per one mole of the gas phase. The solubility mechanism in the range of pressure P under one-half of the solvent’s critical pressure P_c may be easily understood because, at these pressures, the structure of a mixture is very simple: the gaseous mixture of solver and solute fractions with the dimers’ fraction, resulting from the cross- interaction between solver and solute molecules.

At P < P_c/2 the dominating mechanism of solution is filling of the solution molar volume V = RT/P by solute molecules. We refer to this type of solubility as solubility in a free space, created by the solvent molecules, for distribution of the solute molecules with their saturation vapor density.

Experimental data of Coan and King [36] and Wiebe [37] for equilibrium solubility of water in gaseous CO₂, N₂O, and C₂H₆ demonstrate that the solubility at pressures lower than one-half of the solvent’s critical pressure decreases with pressure, then passes through a minimum, and at supercritical pressures increases with pressure (see Figure 4). This paradoxical behavior of solubility has attracted the attention of researchers.

At a fixed subcritical temperature, the minimum water solubility in CO₂ is at a

pressure value slightly less than the solvent’s saturation pressure P_sat(T). At supercritical temperatures, it tends toward the gas-to-liquid transition line [15] , known as the Widom line. This behavior of solubility in subcritical and supercritical CO₂ is known for many other gaseous solute-solvent systems [23] .

Coan and King have explained the solubility pressure dependence in these systems by the liquid phase fugacity dependence on pressure and by high cross- interaction virial coefficients for the molecular interaction of water with gaseous solvents [36] . A higher than the dispersion forces, the cross-interaction of water with CO₂ or N₂O solvents they explain by quadrupole moments [38] of CO₂ and N₂O molecules. The symmetry of ethane molecules forbids not only the dipole moment but also the quadrupole moment. But it does not mean that the molecular interaction of water with ethane has a pure dispersion mechanism. The charged C and H atoms in an ethane molecule, discussed in [39] , create the multipole moment [38] , which can explain the enforced cross-interaction of ethane molecules with molecules of polar solutes.

We suggest a more obvious scheme for the water solution in these solvents, one that presents three main types of the solute-solvent interaction, dominating or essential in different solvent pressure ranges, as demonstrated in Figure 5 for the H₂O-CO₂ system.

3.1. Water Solubility in Gaseous CO₂ at Pressure below P_c/2

At a solution pressure P lower than P_c/2, the following dominates: distribution of solute molecules in a free space of a gaseous solution V_fs(T, P) approximately equal to the solvent’s molar volume V_s(T, P). The larger the V_s(T, P), the more moles of solute vapor may be distributed in this volume. The resulting contribution of this dominating mechanism in the solubility coefficient y_fs (Figure 6) is equal to:

(6)

where D_wsat(T) is the saturated water vapor molar density at temperature T. It can be taken from the NIST database [13] .

The solvent’s molar volume V_s(T, P) increases at low pressures as V_s(T, P) =

RT/P. In real gaseous solutions, V_fs(T, P) deviates from the ideal gas value. In a real gas, the free space for the distribution of solute molecules is created by freely moving particles of a different nature: monomers and clusters of the solvent, solute molecules themselves, and the solute?solvent clusters. In real gaseous solutions, for V_fs, instead of using the solvent’s molar volume V_s, it is more correct to use the free moving particles’ molar volume V_p = 1/D_p, where D_p = P/RT is the free moving particles’ density, responsible for pressure in a real gas [40] . Figure 7 shows the values of the free moving particles’ molar density D_p in gaseous CO₂ at 25˚C, in comparison with the total molar density D and the monomer fraction density D_m. The difference between D and D_p is due to the clusters’ contribution to the total density.

3.2. Water Solubility in Gaseous CO₂ at Pressures below P_c and above P_c/2

Figure 6 shows the comparison of the free space solubility y_fs of water in CO₂ with experimental solubility data at subcritical pressures of the solvent. This figure is typical for many solute-solvent systems at pressures lower than the critical

pressure. It shows that the experimental solubility data at a constant temperature differ from the free space solubility on the close to constant value Δy(P). In the pressure range of almost constant Δy(P) and at a fixed temperature T, we can estimate the average value Δy_av(T). This value is the number of solute moles bound with one mole of solvent molecules by molecular cross-interaction forces (central type in Figure 5). This increment over the free space solubility may be essential, especially close to critical pressures.

The Δy_av(T) to D_wsat(T) ratio is the equilibrium constant for the solute-solvent cross-interaction C_w?cd, reflected in Table 3 for the H₂O-CO₂ system. For the total water solubility y (T, P) in CO₂ at pressures P < P_c, we have the following:

(7)

The corresponding data for two other systems that were analyzed are presented in Table 4.

The expression (7) reflects both the solution’s colligative properties, reflected in RT/P, and individual properties of the solution system, reflected in the solute-solvent cross-interaction equilibrium constant C_w?cd.

Table 3 and Table 4 show that the equilibrium constants for the cross-inte- raction of water molecules in gaseous solutions with CO₂ and N₂O molecules are of the same order of magnitude, but with C₂H₆ molecules they are much smaller. The temperature dependence of equilibrium constants permits us to estimate the cross-interaction parameters: the bond energy E_cross and the corresponding entropic factor, and the effective volume of molecular cross-interaction

these are reflected in Table 5. To find these parameters, we plot ln(C_cross) versus 1000/T (see Figure 8). The linear trend for the experimental data provides the required parameters.

We see that despite a zero dipole moment value for the CO₂ molecule, its cross-interaction bond energy E_cross with polar water molecules is rather high due to the existence of the quadrupole moment [38] in the CO₂ molecule. Hence, the atoms in this molecule are charged.

A high cross-interaction bond energy E_cross in the H₂O-N₂O system results from a combination of dipole and quadrupole potentials of the N₂O molecule. As Table 1 shows, the dipole moment in the N₂O molecule is not very large.

A symmetric ethane molecule possesses no dipole or quadrupole moments. But its cross-interaction bond energy with the water molecule is high enough, although not as high as in H₂O-CO₂ and H₂O-N₂O systems. The cross-bond energy in the H₂O-C₂H₆ system results from the multipole moment [38] of the C₂H₆ molecule, caused by no zero atoms’ charges in this molecule, as discussed in [39] .

3.3. Water Solubility in CO₂ at Supercritical Pressures

In the third type of solution, in three-dimensional (3D) clusters, the number of water molecular bonds with surrounding CO₂ molecules increases (see Figure 5). This results in an increase in water solubility with pressure in high-density gaseous CO₂ (see Figure 9).

Figure 9 demonstrates that at 75˚C and P < 40 bar, the solubility increment Δy(P) is almost constant according to the second type of solubility; however, at P > 40 bar, the increment essentially increases with pressure. Similar behavior of Δy(P) is seen at 50˚C (see Figure 4).

We now consider the solubility increment Δ_3D y caused only by the 3D clusters, by subtracting from the total solubility y the estimated values for the second type of solubility mechanism. According to [16] , at supercritical temperatures the number of 3D clusters rapidly increases as the total density D approaches the critical density.

It is possible to estimate approximately the number of particles in 3D clusters, providing maximum contribution to the solubility increment at supercritical pressures. For this we plot the ln(Δ_3Dy) versus ln(D_m) (see Figure 10) and estimate the tangent of the slope for the linear trend of the graph, K_3D:

The tangent of the slope for the graph is close to 7. Hence the 7-particle clusters provide the maximum contribution to the water solubility in CO₂ at 50˚C and pressures up to 100 bar. The proportionality factor k_3D between D_3D y and is 4.91 × 10⁻⁶ (l/mol)⁷ (see Figure 11).

3.4. Solubility of Ethanol in Sub- and Supercritical CO₂

The theory of three types of solubility developed for the water-CO₂ system may be applied to the ethanol-CO₂ system. The ethanol solubility y (T, P) in gaseous CO₂ has been calculated based on theoretical estimations from [19] for the CO₂ molar share in a gaseous ethanol-CO₂ system at temperatures of 25˚C, 40˚C, 45˚C, and 50˚C. In [19] , the authors used four theoretical models and achieved the best performance with the Peng-Robinson/Mathias-Klotz-Prausnitz approach [41] to estimate the molar share of CO₂ in the gaseous CO₂-ethanol system. Figure 12 demonstrates a good qualitative correspondence of the ethanol solubility pressure dependence with the theory of three types of solubility for polar substances in sub- and supercritical CO₂.

Figure 12 shows an almost constant value for the solubility increment Δy at P < 55 bar and the solubility minimum near P = 60 bar. Comparison of Figure 12 with Figure 4 shows that the solubility of ethanol in gaseous CO₂ at P > 30

bar is greater than the solubility of water at the same temperature and pressure. This is due to the ethanol vapor density being double that of the water vapor density under the same conditions. Furthermore, the solubility increment Δy for the ethanol-CO₂ system is larger than for the water-CO₂ system and larger than the free space solubility y_fs. This indicates that the equilibrium constant for the ethanol-CO₂ dimers is larger than for the H₂O-CO₂ dimers. For a detailed analysis of the cross-interactions in the ethanol-CO₂ dimers, more precise experimental solubility data are required.

3.5. Solubility of Ethanol in Liquid-Like Sub- and Supercritical CO₂

In Section 1.3, the unwanted transformation in chromatography columns of a liquid-like SF to a condensed gas under high pressure was described. This transformation may occur when the pressure falls to the bubble pressure (discussed in [19] ). At the point of this transformation in the chromatography column with a CO₂-modifier system, the modifier’s molar share may be different for the liquid-like and gaseous sections. Under equilibrium conditions, at the bubble pressure, from the two-component liquid-like SF system in the gaseous bubble enters mainly CO₂, and the modifier’s molar share y_gas in the bubble becomes much lower than y_liq in the liquid-like section. This is illustrated in Figure 13, built on the basis of data from [19] , where y_gas is multiplied by a factor of 100 to compare it with the y_liq values at the same pressure.

Figure 13 shows that the 20% - 30% modifier content in the liquid CO₂- ethanol section of the chromatography column may be transformed to the gas phase, with only 1% of modifier in it. A similar process takes place at a subcritical temperature (see Figure 14).

Here again we see that the 20% - 30% CO₂-ethanol liquid section in the chromatography column may be transformed in the bubble point to a 0.4% CO₂- ethanol gaseous system. The content of the analyte may differ significantly from its content in the liquid section, which may distort the chromatography results.

4. Possible Influence of Melting and Triple Point Temperature Harmonic Zigzag Oscillations of a Homologous Series of n-Alkanoic Substances with Different Numbers of Carbon Atoms

N-alkanoic substances are widely used in SF technologies both as the subjects of complex mixtures for analyzing purposes, as principal mobile phases, and as modifiers. Formic acid is an important substance in the performance of negative MS in cases when positive MS fails to produce decisive evidence for the mass ion [42] [43] . This acid has a very low response in a flame ionization detector (FID), permitting us to use it as a modifier in SFC coupled with FID [44] . In HPLC, formic acid is commonly used for buffer preparation and pH regulation. This also applies to acetic acid. Besides n-alkanoic acids, n-alcohols and amines are often used in SFC as modifiers [45] . The influence of modifiers’ individual pro- perties on solubility has a significant impact on extraction and bond separation; this is described in detail in [46] .

Our previous work described the phenomenon of harmonic zigzag oscillations of melting and triple point temperatures for members of a homologous series with different numbers of carbon atoms (N_C) in n-alkanes, n-alkanoic acids, n-alcohols, and in some families of other homologous series of organic substances [39] . The melting and triple point temperatures of substances with even N_C in their chains are higher than the average values of similar substances with the nearest odd numbers. This phenomenon exists in many homologous series and may influence the solubility power of the SF mobile phase with organic modifiers. The solubility power cannot be related to colligative properties because it depends on individual molecular interaction properties of the substances used.

Because of harmonic zigzag progression of temperatures of melting and triple points, it could be of interest to determine the influence on pressure-tempera- ture relations (bar/Kelvin, K) diagrams of three successive members of homologous series after the addition of a range of substances to the supercritical mobile phase, as modifiers to SCCO₂ (substances include n-pentane, n-hexane, and, n-heptane; n-pentanol, n-hexanol, and n-heptanol; and n-pentanoic, n-hex- anoic, and n-heptanoic acids).

We previously described the tangent of the slope change of the melting temperature progression of members of a homologous series before the Nc 5 and after the Nc 5 [39] . The use of these members in a homologous series may also influence the properties of SCCO₂ with organic modifiers. It may be of further interest to explore the effect of the addition of methanol and ethanol as modifiers to SCCO₂ on pressure-temperature differences. Although qualitative calculations for some systems, n-butane [42] , (water + n-butane) and (water + n-hexane) [47] , could show some deviations from CO₂ data, they are useful to see the influence (qualitative only) of different species in a homologous series with different N_C.

Overall, it is important to understand the physical-chemical and thermodynamic aspects of deviation of the first members of a homologous series from regular dependence.

5. Discussion

The mechanism of water and ethanol solubility in dense gaseous CO₂ at sub- and supercritical temperatures, as considered here, is common to many different gaseous solvent-solute systems, if the solute vapor pressure is high enough, as in the case of ethanol. At low solute vapor pressure, the first two types of solution mechanism discussed are not essential; it is the third type of solution that dominates, as in the case of anthracene or phenanthrene, which are widely used in investigations into solubility in SCCO₂ [42] .

Extension of the theory of three types of solution mechanism suggested here to a wide series of solute-solvent high-pressure gaseous systems requires more accurate data on the solubility at sub- and supercritical temperatures and pressures.

The tangent of the slope change of melting temperature progression may have an influence on the choice of modifier (methanol versus ethanol, or methanol/ ethanol versus higher alcohols), in relation to the pressure-temperature diagram (see Figure 3) and results of separation, resolution of bonds in SFC, or quantitative results of extraction by SFE. The tangent of the slope change for N_C below and above N_C 5 was observed in all homologous series described in [39] . The choice of a substance from a homologous series with N_C below or above N_C 5 may dramatically change the results of the procedure.

Cite this paper

Brondz, I., Sedunov, B. and Sivaraman, N. (2017) Influence of Modifiers on Supercritical Fluid Chromatography (SFC) and Supercritical Fluid Extraction (SFE), Part I. International Journal of Analytical Mass Spectrometry and Chromatography, 5, 17-39. https://doi.org/10.4236/ijamsc.2017.52002

References