International Journal of Analytical Mass Spectrometry and Chromatography
Vol.04 No.03(2016), Article ID:70565,12 pages
10.4236/ijamsc.2016.43005
Analytical Approach to Clusters in near Critical CO2
Boris Sedunov, Ilia Brondz*
Norwegian Drug Control and Drug Discovery Institute (NDCDDI), Ski, Norway

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 5, 2016; Accepted: September 11, 2016; Published: September 14, 2016
ABSTRACT
Clusters greatly influence thermophysical properties of near critical gases. The cluster structures of supercritical fluids in general and Carbon Dioxide especially are important for the advanced supercritical fluid technologies and analytics development. The paper extends to near critical densities the developed earlier methods to extract the clusters’ properties from Online Electronic Database of NIST on thermophysical properties of fluids. This Database contains a hidden knowledge of cluster fractions’ properties in real gases. The discovered earlier linear chain clusters dominate at intermediate densities. Their properties can be extrapolated to high density gases, thus opening the way to study large 3D clusters in near critical zone. The potential energy density of a gas, cleared from the chain clusters’ contribution, reflects only the 3D clusters’ characteristics. A series expansion of this value by the Monomer Fraction density discovers properties of n-particle 3D clusters. The paper demonstrates a discrete row of 3D clusters’ particle numbers and gives estimations for bond energies of these clusters.
Keywords:
Real Gas, Supercritical Fluid, Cluster, Bond Energy, Equilibrium Constant, Potential Energy, Theoretical and Analytical Approach to Clusters, Energetic of Clusters, Clusters in Extraction Process, Clusters in Analytical Chemistry

1. Introduction
Supercritical Fluids (SFs) open wonderful possibilities for advanced chemical technologies [1] - [4] and for precise analytical methods [5] - [7] development. These technologies permit to extract needed components from solid and liquid substances, including pharmaceutical products [8] , plant products [9] - [11] , technological waste products [12] , nuclear waste materials [13] . They improve effectiveness of the polymerization processes [4] [12] and catalysts production [14] . In analytical methods SF technology improves the selectiveness of needed products [5] - [8] . The extraction of aromatic substances from leaves and flowers based on clusters in SFs provides a good selectivity and preserves fragrances.
High effectiveness of SF technologies is due to a favorable mixture of properties apparent to both liquids and gases. Among favorable properties of liquids for SF technologies is the high solubility of condensed substances in SFs and among favorable properties of gases is their high diffusivity. The co-acting together of these phenomena permits to extract volatile components from solid or liquid matter and quickly remove them from the extraction zone [1] - [4] . This feature is based on the heterogeneous structure of SFs, consisting of clusters, similar to liquid droplets [15] and freely flying in gaseous zones, or pores and bubbles, filled by gas, in the liquid-like zones [16] [17] .
The penetration into the Cluster World is a fascinating endeavor! But the heterogeneity of SFs complicates the ab initio cluster models extension from dilute to dense gases. Only the inverse way [16] - [22] to study clusters in the SF structures basing on the extra precise experimental thermophysical data [23] has proven to be very effective and informative!
The paper develops the computerized analysis [16] [18] of precise thermophysical data for pure dense gases, contained in the NIST (National Institute of Standards and Technology, USA) Thermophysical Properties of Fluid Systems Database [23] . A high precision of this Database reveals hidden properties of 3D clusters via computer processing of experimental data [19] [20] [24] . The developed methods use the series expansion of precise thermophysical functions [25] by the Monomer fraction density [26] . Due to high precision and smooth character of data from the Database [23] the divergence of the inverse problem results at searching for hidden parameters [27] had been successfully overcome.
To escape from possible errors, the research is based on the Hybrid Intellect method [19] of the big data computerized analysis. The method develops the Visual Analytics [28] and Heuristic Method [29] approaches in application to thermophysical data processing. The method is based on the active researcher-computer interaction during the big data analysis. The graphical analysis of intermediate results stimulates the brain work in searching for better data processing algorithms [19] and provides a correct explanation of discovered phenomena. On this way it got possible to discover a number of unknown before features of molecular interactions in dilute and dense gases and supercritical fluids [19] - [21] .
A large role of clusters in SF technologies and analytics was described in works [30] [31] . The step-by-step movement from dilute gases to supercritical fluids discovers the chain clusters [32] , which contribution to potential energy of a gas may be extrapolated to large densities, thus permitting to analyze the large 3D clusters [16] [17] [33] . This paper demonstrates the mass spectrum of large 3D clusters in the near critical zone of Carbon Dioxide. The mass action law [34] applied to the potential energy density provides estimations for average numbers of particles in dominating 3D clusters at different densities of a gas. The temperature dependence of the corresponding equilibrium constants provides estimations for clusters’ bond energies.
2. The Basics of the Method
2.1. The Equations for Density and Pressure of a Pure Gas
The developed computerized analysis [16] [18] [24] of precise thermophysical data is based on the series expansion of thermophysical functions by the Monomer fraction density Dm [27] . This variable means the density of basic particles of a monocomponent gas in zones, where they do not interact with other particles of a gas. Basic particles of a pure fluid keep their chemical identity, independently on their interactions with other particles. The thermophysical properties of pure fluids in the NIST database [23] are referred to a mole (M) of basic particles.
Statistical Physics [35] , Statistical Mechanics [36] , and Thermal Physics [37] [38] open a wonderful possibility [18] [21] [24] - [26] to find the Monomer fraction density Dm from the isothermal dependence of the total density of basic particles D on pressure P [26] :
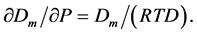 (1)
(1)
Figure 1 shows the Monomer fraction density Dm, the density of free moving particles Dp = P/RT (ideal gas density) and the total density of basic particles D for the near critical CO2.
The difference between the total density D and the Monomer fraction density Dm is the density of basic particles included in different cluster fractions. The density of clusters in the n-particle cluster fraction corresponds to the mass action law [34] and is equal to:
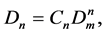 (2)
(2)
where Cn is the coefficient of the n-order term of Dp = P/RT series expansion by Dm, C1 = 1.
Figure 1. Density (thick blue line), Ideal gas density Dp = P/RT (thin red line), Monomer fraction density Dm (dashed green line) versus pressure in the Carbon Dioxide at supercritical T = 312 K.
The density D sums partial densities of the Monomer and all cluster fractions. It is reflected [19] [21] in the system of Equations (3) and (4) for D and P, with Dn given by Equation (2).
 (3)
(3)
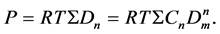 (4)
(4)
2.2. The Clusters’ Properties Extraction from the Potential Energy Density
This research utilizes the potential energy density of a gas to estimate the bond parameters of clusters and equilibrium constants for the cluster fractions. We define the potential energy of a gas U(T, P) as the difference between the Internal energy E(T, P) of a real gas and the Internal energy E(T, 0) of an ideal gas at the same temperature [25] . The defined so potential energy reflects all changes of the real gas Internal energy with pressure, Figure 2.
To apply the mass action law [34] to the potential energy we use its positive density: W(T, P) = −DU(T, P). The series expansion coefficients Wn(T) reflect the contributions of n-particle complexes in the W(T, P). Among these complexes dominate the n-particle clusters, but may be also the n-particle elastic collisions of monomers or elastic collisions of monomers with smaller clusters. For this reason, we have to separate in the Wn(T) coefficients the contributions of physical clusters and virtual clusters reflecting the elastic collisions of monomers with smaller clusters and with each other [19] - [21] .
We expand in series by powers of Dm the W2+ (T, P) function [15] at a constant T, Figure 3:
 (5)
(5)
The sign “+” means that we deal with a function, but not with the second order coefficient:
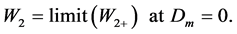 (6)
(6)
Figure 2. The potential energy of the carbon dioxide at supercritical T = 307 K.
Figure 3. The divided by Dm2 potential energy density of CO2 at T = 307 K.
At small densities we can find the first three coefficients for dimers: W2, trimers: W3, and tetramers: W4. The errors in the Wn values estimation grow with the order of the expansion term.
2.3. Estimation of the Clusters’ Bond Energies
We have discovered for many pure gases the zones of temperature, where the Wn coefficients obey to the Boltzmann law. In these zones we can estimate the cluster bond energy En, measured in K, as the tangent of slope for the ln(Wn) dependence on 1/T. An example of this procedure is presented at Figure 4, where the graph for ln(W2) versus 1000/T is depicted for CO2 in the near critical range of temperatures between 270 and 312 K.
The graph seems to be pretty linear and shows that the dimer fraction obeys to the Boltzmann law. But more detailed analysis shows a small nonlinearity resulting in a temperature dependence of the pair bond energy, Figure 5. The temperature dependence of the pair bond energy is due to the anisotropy of the molecular interaction potential of the CO2 molecules [39] .
The deviation of the E2(T) from E2av in this range of T is not more than 2%.
2.4. Estimation of the Cluster Fraction Equilibrium Constants
On dividing the Wn values by the bond energy REn, we receive the cluster fraction equilibrium constant Cun. Index “u” means that these equilibrium constants have been determined basing on the potential energy data. Figure 6 shows the CO2 dimer fraction's equilibrium constant, found from its potential energy temperature dependence.
On dividing the Cu2 by Boltzmann factor exp(E2/T) we come to the attraction zone volume V2 for a particle bound in a dimer. For the CO2 dimers V2 = 0.079 l/mol in the range of temperatures 270 - 312 K. A small value of V2 for CO2, as compared to Noble gases [19] , results from an orientation of bonds in CO2 dimers, limiting the attraction zone volume.
3. Chain Clusters in Carbon Dioxide
In all pure real gases near critical temperature and at densities smaller than one fifth of
Figure 4. Estimation of the pair bond energy for dimers in the near critical Carbon Dioxide.
Figure 5. The pair bond energy E2 (T) (thick blue line) and the average bond energy E2av = 340.6 K (thin red line) in Carbon Dioxide at temperatures 270 - 312 K.
Figure 6. The CO2 dimer fraction’s equilibrium constant, found from its potential energy temperature dependence.
the critical density dominate linear chain clusters [32] . They are characterized by almost linear dependence of the W2/W2+ ratio versus Dm, Figure 7.
This linear dependence reflects a universal law of a new particle interaction with an existing chain cluster at its attaching to end molecules of the chain [16] [32] . But more careful analysis shows that this dependence is quadratic:
 (7)
(7)
Figure 7. A close to linear dependence of the W2/W2+ ratio on the Monomer fraction density Dm in Carbon Dioxide at T = 300 K.
The quadratic term reflects a slight interaction of new molecule with the next molecules in the chain. The temperature dependences of the chain interaction volume Vu and k2 in CO2 are shown at Figure 8.
Having found parameters of chain interaction Vu and k2, we can extrapolate the chain clusters contribution W2+l in the W2+(T, Dm) function to larger densities, up to the critical density:
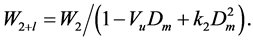 (8)
(8)
4. Large 3D Clusters in Carbon Dioxide
The W2+ − W2+l function reflects the contribution of large 3D clusters in W2+(T, Dm), Figure 9.
4.1. Analytical Mass Spectrometry of 3D Clusters in CO2
Extra high nonlinearity of the W2+3D(T, Dm) function gives unstable results at a direct series expansion by Dm. To estimate properties of 3D clusters we had to develop new method of the step-by-step analysis of this function. First, we analyze the ln(W2+3D) versus ln(Dm) dependence, Figure 10.
The lower part of the graph is almost linear. It reflects the contribution of the smallest 3D clusters in the potential energy. The tangent of slope for this part of the graph we find as the minimum of the ln(W2+3D) by ln(Dm) first derivative. And we conclude that the average number N13D of particles in the smallest 3D clusters equals to:
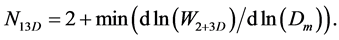 (9)
(9)
Figure 11 shows the estimations at different temperatures and the average value for N13D.
Then we find the corresponding equilibrium coefficient:
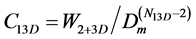 at Dm in the point of N13Dmin. (10)
at Dm in the point of N13Dmin. (10)
We extrapolate the function 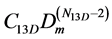 to larger densities and exclude it from the
to larger densities and exclude it from the
Figure 8. The temperature dependences of the chain interaction volume Vu (thick blue line) and 100k2 (thin red line) in CO2.
Figure 9. The contribution W2+3D of large 3D clusters in W2+ (T, Dm) in CO2 at T = 305 K.
Figure 10. The ln (W2+3D) versus ln (Dm) dependence in CO2 at T = 305 K.
Figure 11. Numbers of particles N13D of the smallest 3D clusters in CO2 estimated for different temperatures (markers) and their average value (solid red line).
W2+3D just to find the contribution of larger clusters. So, step-by-step we determine numbers Nn3D of particles in all 3D clusters, Figure 12, and corresponding equilibrium coefficients Cn3D.
As we see, the spread of results grows with the number n of the 3D cluster type. But, nevertheless, we see a discrete row of particle numbers in 3D clusters. In other words, near critical density we have a discrete row of dominating 3D clusters! The maximal number of particles in 3D clusters grows with approaching the critical temperature, where it exceeds 103.
4.2. Bond Energies of 3D Clusters
Temperature dependences of equilibrium coefficients Cn3D give us estimations for corresponding 3D cluster bond energies, Figure 13.
The numbers of particles Nn3D and bond energies En3D grow with the number n of the 3D cluster type nonlinearly, Figure 14.
But the bond energy En3D dependence on the number of particles Nn3D is almost linear with a coefficient 850 K per particle, Figure 15. If we compare this energy with the pair interaction energy E2 = 340.6 K, estimated at Figure 4, we can state that in 3D CO2 clusters every particle has approximately 5 bonds with neighbors.
A large number of bonds per particle in 3D clusters explain the soluble power of the gas-like supercritical fluids. So, dense gases with their density under the critical one possess soluble power due to large share of particles included in 3D clusters.
Figure 12. Numbers of particles Nn3D of first four types of 3D clusters in CO2 estimated for different temperatures (markers).
Figure 13. Estimation of bond energies for first four types of 3D clusters in CO2.
Figure 14. The numbers of particles Nn3D (blue rhomb markers) and bond energies En3D (red round markers) in the first four types of 3D clusters in CO2.
Figure 15. Almost linear dependence of the 3D clusters' bond energy on the number of particles.
5. Conclusions
・ The Monomer fraction density based computerized analysis of precise data from modern electronic thermophysical databases provides estimation of large 3D clusters’ characteristics in the near critical zone;
・ The dominating types of 3D clusters in the near critical Carbon Dioxide possess a discrete row of particle numbers with approximately 5 pair bonds per every particle;
・ The power of the developed Analytical Mass Spectrometry method for large 3D clusters will grow due to an inevitable growth of experimental thermophysical data precision.
Cite this paper
Sedunov, B. and Brondz, I. (2016) Analytical Approach to Clusters in near Critical CO2. International Journal of Analytical Mass Spectrometry and Chromatography, 4, 39-50. http://dx.doi.org/10.4236/ijamsc.2016.43005
References
- 1. McHugh, M.A. and Krukonis, V.J. (1986) Supercritical Fluid Extraction: Principles and Practice. Butterworth Publishers, Stoneham.
- 2. Taylor, L.T. (1996) Supercritical Fluid Extraction. John Wiley & Sons Ltd., New York.
- 3. McHardy, J. and Sawan, S.P., Eds. (1998) Supercritical Fluid Cleaning. Fundamentals, Technology and Applications. Noyes Publications, Westwood.
- 4. Gumerov, F.М., Sabirzyanov, А.N. and Gumerova, G.I. (2007) Sub- and Supercritical Fluids in Polymer Processing. 2nd Edition, Publishing House “FAN”, Kazan.
- 5. Brondz, I. and Brondz, A. (2012) Supercritical Fluid Chromatography-Mass Spectrometry (SFC-MS) of Heterocyclic Compounds with Trivalent and Pentavalent Nitrogen in Cough Relief Medical Forms Tuxi and Cosylan. American Journal of Analytical Chemistry, 3, 870-876.
http://dx.doi.org/10.4236/ajac.2012.312A115 - 6. Brondz, I. and Brondz, A. (2014) Review: Isomer Separation, Chiral Resolution, and Structure Elucidation Analyses are the Future of Analytical Supercritical Fluid Chromatography-Mass Spectrometry. International Journal of Analytical Mass Spectrometry and Chromatography, 2, 15-24.
http://dx.doi.org/10.4236/ijamsc.2014.21002 - 7. Brondz, I. (2009) Chapter 5, SFC-MS Analysis of Contaminants in Primaquine Diphosphate Tablets and Spectral UV and NMR Characterizing of Primaquine and Quinocide. In: Csizmadia, E. and Kalnoky, I., Eds., Antimalarial Drugs: Costs, Safety and Efficacy, Nova Science Publishers, Inc., Hauppauge, 105-124.
- 8. Brondz, I. and Brondz, A. (2012) The Technology for Preparation of Generic (Monoenantiomeric) Antimalarial Drug Primaquine by Using Supercritical Fluid Chromatography. Separation of Primaquine from Quinocide: Simultaneous Resolution of the Enantiomers of Primaquine and Their Separation from Quinocide in One Run. American Journal of Analytical Chemistry, 3, 884-890.
http://dx.doi.org/10.4236/ajac.2012.312A117 - 9. Andradea, K.S., Gonçalveza, R.T., Maraschinb, M., Ribeiro-do-Vallec, R.M., Martínezd, J. and Ferreiraa, S.R.S. (2012) Supercritical Fluid Extraction from Spent Coffee Grounds and Coffee Husks: Antioxidant Activity and Effect of Operational Variables on Extract Composition. Talanta, 88, 544-552.
http://dx.doi.org/10.1016/j.talanta.2011.11.031 - 10. Couto, R.M. Fernandes, J. Gomes da Silva, M.D.R. and Simões, C. (2009) Supercritical Fluid Extraction of Lipids from Spent Coffee Grounds. The Journal of Supercritical Fluids, 51, 159-166.
http://dx.doi.org/10.1016/j.supflu.2009.09.009 - 11. Araújo, J.M.A. and Sandi, D. (2007) Extraction of Coffee Diterpenes and Coffee Oil Using Supercritical Carbon Dioxide. Food Chemistry, 101, 1087-1094. http://dx.doi.org/10.1016/j.foodchem.2006.03.008
- 12. Gumerov, F.M., Kayumov, R.A., Usmanov, R.A., Sagdeev, A.A., Abdullin, I.S.H. and Sharafeev, R.F. (2012) Waste Management in Propylene Epoxidation Process with the Use of Supercritical Fluid Media. American Journal of Analytical Chemistry, 3, 950-957.
http://dx.doi.org/10.4236/ajac.2012.312A126 - 13. Sujatha, K., Pitchaiah, K.C., Sivaraman, N., Srinivasan, T.G. and Rao, P.R.R.V. (2012) Recovery of Uranium and Plutonium from Waste Matrices Using Supercritical Fluid Extraction. American Journal of Analytical Chemistry, 3, 916-922. http://dx.doi.org/10.4236/ajac.2012.312A121
- 14. Zakharov, A.A., Jaddoa, A.A., Bilalov, T.R. and Gumerov, F.М. (2014) Synthesis of the Palladium Catalyst with the Supercritical СO2-Impregnation Method Realized in the Static Mode. International Journal of Analytical Mass Spectrometry and Chromatography, 2, 113- 122.
http://dx.doi.org/10.4236/ijamsc.2014.24010 - 15. Sedunov, B. (2015) Clusters—The Seeds of Droplets and Snowflakes. The Voice of the Publisher, 1, 66-76.
http://dx.doi.org/10.4236/vp.2015.13009 - 16. Sedunov, B. (2012) The Analysis of the Equilibrium Cluster Structure in Supercritical Carbon Dioxide. American Journal of Analytical Chemistry, 3, 899-904. http://dx.doi.org/10.4236/ajac.2012.312A119
- 17. Sedunov, B. (2013) The Equilibrium Thermal Physics of Supercritical Fluids. International Journal of Analytical Mass Spectrometry and Chromatography, 1, 103-108.
http://dx.doi.org/10.4236/ijamsc.2013.12013 - 18. Sedunov, B. (2013) Thermal Analysis of Thermophysical Data for Equilibrium Pure Fluids. Journal of Modern Physics, 4, 8-15. http://dx.doi.org/10.4236/jmp.2013.47a2002
- 19. Sedunov, B. (2015) Discovering the Cluster World. Lambert Academic Publishing, Saarbrucken 108.
- 20. Sedunov, B. (2016) The Wonders of Molecular Interactions. Lambert Academic Publishing, Saarbrucken, 104.
- 21. Sedunov, B. (2014) The Physics of Clusters in Real Gases. Atiner’s Conference Paper Series, No. PHY2014-1280, Athens.
http://www.atiner.gr/papers/PHY2014-1280.pdf - 22. Sedunov, B. (2013) Nanosized Objects in Equilibrium Supercritical Fluids. MATEC Web of Conferences, 3, Article Number: 01062. http://dx.doi.org/10.1051/matecconf/20130301062
- 23. Webbook. NIST (2011) Thermophysical Properties of Fluid Systems.
http://webbook.nist.gov/chemistry/fluid - 24. Sedunov, B.I. (2013) The Numerical Integration Method of the First-Order ODE for Numerical Analysis of Thermophysical Data. Vestnik RosNOU, 25-28.
- 25. Sedunov, B. (2012) Equilibrium Molecular Interactions in Pure Gases. Journal of Thermodynamics, 2012, Article ID: 859047.
http://dx.doi.org/10.1155/2012/859047 - 26. Sedunov, B. (2008) Monomer Fraction in Real Gases. International Journal of Thermodynamics, 11, 1-9.
- 27. Aster, R.C., Borchers, B. and Thurber, C. (2012) Parameter Estimation and Inverse Problems. 2nd Edition, Elsevier, Amsterdam.
- 28. Keim, D., Kohlhammer, J., Ellis, G. and Mansmann, F. (Eds.) (2010) Mastering the Information Age: Solving Problems with Visual Analytics. Eurographics Association Goslar.
- 29. Dzemyda, G. and Sakalauskas, L. (2011) Large-Scale Data Analysis Using Heuristic Methods. Vilnius University, Informatica, 22, 1-10.
- 30. Brondz, I. (2016) Review: Adducts and Clusters in Chromatography, Mass Spectrometry and Nature. International Journal of Analytical Mass Spectrometry and Chromatography, 4, 27-33.
http://dx.doi.org/10.4236/ijamsc.2016.42003 - 31. Brondz, I. (2016) Review: Discovering the Cluster World. Clusters’ Hidden Parameters Extraction from Thermophysical Data and the Wonders of Molecular Interactions. The Experimentally Based Molecular Interaction Features. International Journal of Analytical Mass Spectrometry and Chromatography, 4, 34-38. http://dx.doi.org/10.4236/ijamsc.2016.42004
- 32. Sedunov, B. (2015) The Molecular Physics of Chain Clusters. Atiner’s Conference Paper Series, No. PHY2015-1711, Athens.
- 33. Sedunov, B. (2013) Equilibrium Structure of Dense Gases. MATEC Web of Conferences, 3, Article Number: 01002.
http://dx.doi.org/10.1051/matecconf/20130301002 - 34. Koudryavtsev, A.B. Jameson, R.F. and Linert, W. (2001) The Law of Mass Action. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-56770-4 - 35. Landau, L.D. and Lifshitz, E.M. (1980) Statistical Physics. Pergamon Press, London.
- 36. Feynman, R. (1972) Statistical Mechanics: A Set of Lectures. W.A. Benjamin Inc., New York.
- 37. Kittel, C. (1970) Thermal Physics. John Wiley and Sons Inc., New York.
- 38. Kittel, C. and Kroemer, H. (1980) Thermal Physics. W.M. Freeman and Co., New York.
- 39. Gray, C.G. and Gubbins, K.E. (2011) Theory of Molecular Fluids. 2 Volumes, Oxford University Press, Oxford.
















