International Journal of Analytical Mass Spectrometry and Chromatography
Vol.04 No.01(2016), Article ID:64632,13 pages
10.4236/ijamsc.2016.41001
Condensed Matrix Descriptor for Protein Sequence Comparison
Soumen Ghosh1, Jayanta Pal2, Bansibadan Maji3, Dilip Kumar Bhattacharya4
1Department of Information Technology, Narula Institute of Technology, Kolkata, India
2Department of Computer Science & Engineering, Narula Institute of Technology, Kolkata, India
3Department of Electronics & Communication Engineering, National Institute of Technology, Durgapur, India
4Department of Pure Mathematics, Calcutta University, Kolkata, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 December 2015; accepted 14 March 2016; published 17 March 2016
ABSTRACT
The present paper develops a novel way of reducing a protein sequence of any length to a real symmetric condensed 20 × 20 matrix. This condensed matrix can be nicely applied as a protein sequence descriptor. In fact, with such a condensed representation, comparison of two protein se- quences is reduced to a comparison of two such 20 × 20 matrices. As each square matrix has a unique Alley Index/normalized Alley Index, such index is conveniently used in getting distance matrix to construct Phylogenetic trees of different protein sequences. Finally protein sequence comparison is made based on these Phylogenetic trees. In this paper three types viz., NADH dehydrogenase subunit 3 (ND3), subunit 4 (ND4) and subunit 5 (ND5) of protein sequences of nine species, Human, Gorilla, Common Chimpanzee, Pygmy Chimpanzee, Fin Whale, Blue Whale, Rat, Mouse and Opossum are used for comparison.
Keywords:
Amino Acids, Condensed Matrix, Eigen Values, Matrix Invariants, ALE Index

1. Introduction
A protein is a linear chain of 20 amino acids, which starts with a start codon ATG, which corresponds to the amino acid methionine, followed by a sequence of amino acids and ends with a stop codon. The amino acid sequence that makes a protein is called its primary structure. Protein sequence analysis means analysis of its primary structure. It provides important insight into the structure of proteins, which in turn, greatly facilitates the understanding of its biochemical and cellular function. Efforts to use computational methods in predicting protein structure, which are based only on sequence information, started several years ago. Sequence alignment is a way of arranging the sequences of DNA, RNA, or protein to identify regions of similarity that may be a consequence of functional, structural, or evolutionary relationships between the sequences [1] . Existing methods for sequence comparison can be classified into alignment based methods and alignment-free methods. Alignment- based methods use dynamic programming, a regression technique that finds an optimal alignment by assigning scores to different possible alignments and picking the alignment with the highest score. Dynamic programming method is an accurate method for comparison of two sequences. There are two types of dynamic programming: global dynamic programming which is applied for comparing sequences as a whole [2] [3] and local dynamic programming which is applied to compare selected portions of the sequences [4] . For multiple sequence alignments (MSA) there are many methods, some of them are given in [5] -[7] . In parallel there are many algorithms available for multiple sequence comparison; some of them are listed in [8] -[11] . But the main difficulty in multiple sequence alignment is the computational complexity. In fact a naïve MSA takes O(lN) time for completion of the program, where N is the number of sequences for comparison, each having a length l. Therefore as an alternative to sequence based alignment, alignment free methods are chosen. Such alignment free methods are already known for comparison of DNA/RNA sequence comparison [12] -[14] . Alignment free methods are based on graphical representation, which is obtained from the numerical values given to the nucleotides. Next step is to obtain the descriptors for obtaining distance matrices. One way is to characterize the graphs by obtaining directly some invariants like geometrical centres, graph radii, variances etc. [15] and to use these invariants as descriptors to obtain distance matrices for constructing phylogenetic trees of comparison. The other way is to transform the graphical representation into another mathematical object, a real symmetric matrix. The matrices may be of L/L, M/M or J/J types [16] . J/J matrix is applicable only for 3D representation. Once a real symmetric matrix M is obtained, there are different invariants associated with this matrix such as the average matrix element, the average row sum, the leading eigen value, Weiner number and the Alley index/normalized Alley index [17] . These may be used to obtain the distance matrix to obtain phylogenetic trees for comparison of DNA/RNA sequences. Now protein sequences are to some degree similar to DNA/RNA sequences in the sense that DNA/RNA sequences contain four nucleotides, whereas protein sequences contain twenty amino acids. Thus the graphical representation methods for comparison of DNA/RNA may be extended to protein sequences as well.
Currently, many researchers have proposed different methods for the graphical representation of protein sequences [18] -[33] . In most of these existing methods, the main drawbacks are that the higher the dimension of the protein sequence graphs, the heavier the computation complexity of the methods or the lower the recognition degree of the protein sequence graphs [34] [35] . In the methods proposed in [36] -[38] , the main drawbacks are that the 3D graphics seem to be more complex and have lower visibility than the 2D graphics, and, in addition, to obtain the sequence invariants from the graphics, complex matrices are required to be constructed, which need much computation and storage.
Lei Wang, Hui Peng and Jinhua Zheng [39] proposed a novel method for analyzing the similarity/dissimilar- rity by combining the idea of the sequence alignment and the graphical representation methods to avoid the weakness of both of these two methods to some degree. Principal components analysis (PCA) is a standard tool in multivariate data analysis to reduce the number of dimensions, which has been proved to be effective in the process of protein sequence analysis [40] -[42] . They used 29 different spike proteins, which are widely used as the test data [25] -[34] [43] .
Anyway it is very difficult to make direct comparison of protein sequences owing to their very long sizes and unequal lengths. Actually a direct comparison between protein sequences would not only be tedious but would involve steps not yet fully resolved, such as how to proceed when comparing sequences of different lengths. A possible strategy to avoid such difficulties is to represent the protein sequences by suitable condensed matrices. In this way, comparison between sequences reduces to comparison between matrices. Similar reduction of DNA sequence to 4 × 4 matrices is already known [44] . The case was simple in the sense that it was needed to consider representation of four nucleotides only, where as in the case of protein sequence it is much more difficult to handle twenty amino acids simultaneously. To make the problem manageable, we start with a suitable numerical representation of the sequence and finally reduce it in the form of a condensed 20 × 20 matrix of unique size.
2. Methods of Constructing 20 × 20 Matrices of Protein Sequences
Construction of 20 × 20 matrix of protein sequences involves four primary steps. For the sake of convenience, we explain the steps with reference to the small sample shown in Table 1. As it contains only 9 distinct amino acids, so in this case, the final reduction is a 9 × 9 matrix.
2.1. First Step: To Calculate Distance of Each Label from the Neighboring Labels
In the first step we construct “distance” of each label from the neighboring labels of the same and different kind of amino acid. It is calculated by numbering the amino acids in the protein sequence starting from 0 (zero) for the first amino acid and starting from 1 (one) for the other amino acids. Thereby we get a 12 × 12 matrix, where 12 is the length of the protein sequence (as shown in Table 2). The entries of the matrix represent frequencies of occurrences of amino acids.
2.2. Second Step: To Group Together All Similar Amino Acids
Second step involves grouping together all similar amino acids. First of all, the amino acids are taken alphabetically as D, E, K, L, M, P, R, V, W. Next the bases of the same kind are grouped together. The elements of the matrix correspond to the serial distance of the first 12 amino acids. The rearranged 12 × 12 matrix is shown in Table 3.
2.3. Third Step: To Obtain Sub-Matrices
From Table 3, we obtain forty five sub-matrices (DD, DE, DK, DL, DM, DP, DR, DV, DW, EE, EK, EL, EM, EP, ER, EV, EW, KK, KL, KM, KP, KR, KV, KW, LL, LM, LP, LR, LV, LW, MM, MP, MR, MV, MW, PP, PR, PV, PW, RR, RV, RW, VV, VW, WW). Some of them are shown in Tables 4-6.
2.4. Fourth Step: To Obtain Final Reduced 9 × 9 Condensed Matrix
All the sub-matrices are not square matrices. So we cannot get Eigen values of all the sub-matrices. Mathematically it may be shown that the average of all the elements of a square matrix nearly approximates the highest Eigen value of that matrix. So in the third step we consider the average of all the elements of each sub-matrix
Table 1. Small sample of protein sequences.
Table 2. 12 × 12 matrix obtained by considering the 12 amino acids from the beginning of the sequence of Table 1.
Table 3. Rearranged 12 ×12 matrix.
Table 4. DE sub-matrix.
Table 5. EP sub-matrix.
Table 6. PR sub-matrix.
and finally get the 9 × 9 condensed matrix given in Table 7.
3. Construction of 20 × 20 Condensed Matrix for (HIV 1) Tat Protein
We consider the sequence of Human Immunodeficiency Virus 1 (HIV 1) Tat Protein, which has 86 amino acids. By following steps one to three as above, we get 86 × 86 rearranged matrix and calculate the sub-matrices Two such sub-matrices AA and CG are given in Table 8 and Table 9 respectively;
The final 20 × 20 condensed matrix is given in Table 10.
4. Sensitivity of the 20 × 20 Condensed Matrix
Now we change the protein sequence of Human Immunodeficiency Virus 1 a little bit. We interchange the 5th and 56th amino acid i.e. we take the 5th amino acid as R instead of D and take the 56th amino acid as D instead of R and we get the following (Table 11).
We get the following final 20 × 20 condense matrix (Table 12) of the sequence of Table 11.
Table 7. 9 × 9 Condensed matrix.
Table 8. AA sub-matrix.
Table 9. CG sub-matrix.
To test for sensitivity, we generate a 20 × 20 matrix, which contains the cell-by-cell differences of the content of Table 10 and Table 12. This is given in Table 13.
The result shows that our method of constructing the 20 × 20 Condensed Matrix is highly sensitive. Little bit of change in the sequence of a protein affects the content of the final 20 × 20 condense matrix.
5. Comparison of Protein Sequences
As we have already illustrated how to reduce a protein sequence to a condensed 20 × 20 matrix, so the problem of comparison of two protein sequences reduces to the problem of comparison of two 20 × 20 matrices. In this paper we solve this problem by ALE index [17] .
ALE index for a matrix M is defined by
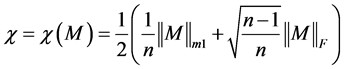
where,
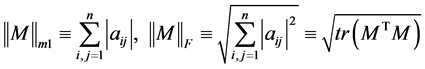 .
.
Table 10. 20 × 20 condense matrix of the protein sequence of Human Immunodeficiency Virus 1 (HIV 1) tat protein.
Table 11. Modified or changed protein sequence of Human Immunodeficiency Virus 1 (HIV 1) tat protein (length 86 amino acids).
The ALE-index is very simple for calculation so that it can be directly used to handle long sequences. If desired, one can introduce weighting procedure that will normalize magnitudes of the ALE-indices to reduce variations caused by comparison of matrices of different sizes. For instance, one can consider instead of χ a normalized ALE-index χ' = χ/n, where n is the length of the sequence and the order of the corresponding matrix as well.
6. Sequences for Comparison
We have used the NADH dehydrogenase subunit 3 (ND3), subunit 4 (ND4) and subunit 5 (ND5) protein sequences of nine species for comparison as shown in Table 14.
7. Measures of Comparison of Sequences from Reduced Matrices
First we construct 20 × 20 matrices for nine protein sequences of ND3, ND4 and ND5. Then we calculate the differences of each pair of protein sequences. For example, the difference of 20 × 20 matrices of Human and Gorilla for ND5 protein sequences is shown in Table 15. In this way we get 36 matrices for each type of protein (ND3, ND4 and ND5). Then we calculate the χ' values of 36 matrices for each type of protein (ND3, ND4 and
Table 12. 20 × 20 Condense matrix of modified or changed protein sequence of Human Immunodeficiency Virus 1 (HIV 1).
Table 13. 20 × 20 matrix of the differences of Table 8 and Table 10.
Table 14. List of nine species with their versions and lengths.
Table 15. Difference of 20 × 20 matrices of human and gorilla (ND5).
ND5). The results for ND3, ND4 and ND5 are shown in Tables 16-18 respectively. Then we construct the phylogenetic trees for each type of proteins (ND3, ND4 and ND5) for nine different species (Human, Gorilla, Common Chimpanzee, Pygmy Chimpanzee, Fin Whale, Blue Whale, Rat, Mouse and Opossum). The results are shown in Figures 1-3 respectively.
Table 16. ALE index of pair of nine species (ND3).
Table 17. ALE index of pair of nine species (ND4).
8. Discussion
In this paper we introduce a novel characterization for Protein Sequence using condensed matrices that are based on average distances for pairs of bases obtained as quotients of sequential numbers and serial numbers in primary sequences. Such matrices not only offer some insight into the nature of the protein sequence but also allow one to make qualitative and quantitative comparisons between different sequences of proteins, whether within the same species or between different species.
The method of construction of 20 × 20 condensed matrix of the protein sequence reveals that
・ The representation of the protein sequence in 20 × 20 condensed matrix is unique.
・ The condensed form of representation may help in comparing two protein sequences of unequal lengths.
・ It is applicable to sequence of any finite length, however large it may be.
・ The phylogenetic trees (Figures 1-3) of nine species of three different types of proteins (ND3, ND4 and ND5) agree with the standard phylogenetic tree of the same species.
・ It is comparatively an easier form of comparison of protein sequences.
Table 18. ALE index of pair of nine species (ND5).
Figure 1. Phylogenetic tree of nine species (ND3).
Figure 2. Phylogenetic tree of nine species (ND4).
Figure 3. Phylogenetic tree of nine species (ND5).
9. Conclusion
Condensed matrix representation of protein sequences is a useful tool. It is applicable to comparison of protein sequences of equal or unequal lengths and of any finite size, however large it may be. It is also an accurate one in comparing the protein sequences of the aforesaid types.
Cite this paper
SoumenGhosh,JayantaPal,BansibadanMaji,Dilip KumarBhattacharya, (2016) Condensed Matrix Descriptor for Protein Sequence Comparison. International Journal of Analytical Mass Spectrometry and Chromatography,04,1-13. doi: 10.4236/ijamsc.2016.41001
References
- 1. Mount, D.M. (2004) Bioinformatics: Sequence and Genome Analysis. 2nd Edition, Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY, USA.
- 2. Needleman, S.B. and Wunsch, C.D. (1970) A General Method Applicable to the Search for Similarities in the Amino Acid Sequence of Two Proteins. Journal of Molecular Biology, 48, 443-453.
http://dx.doi.org/10.1016/0022-2836(70)90057-4 - 3. Gotoh, O. (1982) An Improved Algorithm for Matching Biological Sequences. Journal of Molecular Biology, 162, 705-708. http://dx.doi.org/10.1016/0022-2836(82)90398-9
- 4. Smith, T.F. and Waterman, M.S. (1981) Identification of Common Molecular Subsequences. Journal of Molecular Biology, 147, 195-197. http://dx.doi.org/10.1016/0022-2836(81)90087-5
- 5. Bucka-Lassen, K., Caprani, O. and Hein, J. (1999) Combining Many Multiple Alignments in One Improved Alignment. Bioinformatics, 15, 122-130. http://dx.doi.org/10.1093/bioinformatics/15.2.122
- 6. Wang, L. and Jiang, T. (1994) On the Complexity of Multiple Sequence Alignment. Journal of Computational Biology, 1, 337-348. http://dx.doi.org/10.1089/cmb.1994.1.337
- 7. Shyu, C., Sheneman, L. and Foster, J.A. (2004) Multiple Sequence Alignment with Evolutionary Computation. Genetic Programming and Evolvable Machines, 5, 121-144.
http://dx.doi.org/10.1023/B:GENP.0000023684.05565.78 - 8. Higgins, D.G. and Sharp, P.M. (1988) CLUSTAL: A Package for Performing Multiple Sequence Alignment on a Micro-Computer. Gene, 73, 237-244. http://dx.doi.org/10.1016/0378-1119(88)90330-7
- 9. Edgar, R.C. (2004) MUSCLE: Multiple Sequence Alignment with High Accuracy and High Throughput. Nucleic Acids Research, 32, 1792-1797. http://dx.doi.org/10.1093/nar/gkh340
- 10. Katoh, K., Misawa, K., Kuma, K.-I. and Miyata, T. (2002) MAFFT: A Novel Method for Rapid Multiple Sequence Alignment Based on Fast Fourier Transform. Nucleic Acids Research, 30, 3059-3066. http://dx.doi.org/10.1093/nar/gkf436
- 11. Notredame, C., Higgins, D.G. and Heringa, J. (2000) T-Coffee: A Novel Method for Fast and Accurate Multiple Sequence Alignment. Journal of Molecular Biology, 302, 205-217.
http://dx.doi.org/10.1006/jmbi.2000.4042 - 12. Pham, T.D. and Zuegg, J. (2004) A Probabilistic Measure for Alignment-Free Sequence Comparison. Bioinformatics, 20, 3455-3461. http://dx.doi.org/10.1093/bioinformatics/bth426
- 13. Reinert, G., Chew, D., Sun, F. and Waterman, M.S. (2009) Alignment-Free Sequence Comparison (I): Statistics and Power. Journal of Computational Biology, 16, 1615-1634.
http://dx.doi.org/10.1089/cmb.2009.0198 - 14. Vinga, S. and Almeida, J. (2003) Alignment-Free Sequence Comparison—A Review. Bioinformatics, 19, 513-523. http://dx.doi.org/10.1093/bioinformatics/btg005
- 15. Nandy, A., Harle, M. and Basak, S.C. (2006) Mathematical Descriptors of DNA Sequences: Development and Applications. ARKIVOC, (ix) 211-238.
- 16. Luo, J., Guo, J. and Li, Y. (2010) A New Graphical Representation and Its Application in Similarity/Dissimilarity Analysis of DNA Sequences. 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, 18-20 June 2010, 1-5. http://dx.doi.org/10.1109/icbbe.2010.5515203
- 17. Li, C., Xing, L.L. and Wang, X. (2008) 2-D Graphical Representation of Protein Sequences and Its Application to Coronavirus Phylogeny. BMB Reports, 41, 217-222.
http://dx.doi.org/10.5483/BMBRep.2008.41.3.217 - 18. Randic, M., Vracko, M., Novic, M. and Plavsic, D. (2009) Spectral Representation of Reduced Protein Models. SAR and QSAR in Environmental Research, 20, 415-427.
http://dx.doi.org/10.1080/10629360903278685 - 19. Randic, M., Mehulic, K., Vukicevic, D., Pisanski, T., Vikic-Topic, D. and Plavsic, D. (2009) Graphical Representation of Proteins as Four-Color Maps and Their Numerical Characterization. Journal of Molecular Graphics and Modelling, 27, 637-641. http://dx.doi.org/10.1016/j.jmgm.2008.10.004
- 20. Bai, F. and Wang, T. (2006) On Graphical and Numerical Representation of Protein Sequences. Journal of Biomolecular Structure and Dynamics, 23, 537-545.
http://dx.doi.org/10.1080/07391102.2006.10507078 - 21. Randic, M. (2007) 2-D Graphical Representation of Proteins Based on Physico-Chemical Properties of Amino Acids. Chemical Physics Letters, 440, 291-295. http://dx.doi.org/10.1016/j.cplett.2007.04.037
- 22. Ghosh, A. and Nandy, A. (2011) Graphical Representation and Mathematical Characterization of Protein Sequences and Applications to Viral Proteins. Advances in Protein Chemistry and Structural Biology, 83, 1-42. http://dx.doi.org/10.1016/B978-0-12-381262-9.00001-X
- 23. Li, C., Yu, X., Yang, L., Zheng, X. and Wang, Z. (2009) 3-D Maps and Coupling Numbers for Protein Sequences. Physica A: Statistical Mechanics and Its Applications, 388, 1967-1972.
- 24. Randic, M., Zupan, J. and Vikic-Topic, D. (2007) On Representation of Proteins by Star-Like Graphs. Journal of Molecular Graphics and Modelling, 26, 290-305.
- 25. Li, C., Xing, L. and Wang, X. (2008) 2-D Graphical Representation of Protein Sequences and Its Application to Coronavirus Phylogeny. Journal of Biochemistry and Molecular Biology, 41, 217-222. http://dx.doi.org/10.5483/bmbrep.2008.41.3.217
- 26. Wen, J. and Zhang, Y. (2009) A 2D Graphical Representation of Protein Sequence and Its Numerical Characterization. Chemical Physics Letters, 476, 281-286.
http://dx.doi.org/10.1016/j.cplett.2009.06.017 - 27. Wu, Z.-C., Xiao, X. and Chou, K.-C. (2010) 2D-MH: A Web-Server for Generating Graphic Representation of Protein Sequences Based on the Physicochemical Properties of Their Constituent Amino Acids. Journal of Theoretical Biology, 267, 29-34. http://dx.doi.org/10.1016/j.jtbi.2010.08.007
- 28. Liao, B., Sun, X. and Zeng, Q. (2010) A Novel Method for Similarity Analysis and Protein Sub-Cellular Localization Prediction. Bioinformatics, 26, 2678-2683. http://dx.doi.org/10.1093/bioinformatics/btq521
- 29. Novic, M. and Randic, M. (2008) Representation of Proteins as Walks in 20-D Space. SAR and QSAR in Environmental Research, 19, 317-337. http://dx.doi.org/10.1080/10629360802085066
- 30. Qi, Z.-H., Feng, J., Qi, X.-Q. and Li, L. (2012) Application of 2D Graphic Representation of Protein Sequence Based on Huffman Tree Method. Computers in Biology and Medicine, 42, 556-563. http://dx.doi.org/10.1016/j.compbiomed.2012.01.011
- 31. Yu, H.-J. and Huang, D.-S. (2012) Novel 20-D Descriptors of Protein Sequences and It’s Applications in Similarity Analysis. Chemical Physics Letters, 531, 261-266.
http://dx.doi.org/10.1016/j.cplett.2012.02.030 - 32. He, P.-A., Wei, J., Yao, Y. and Tie, Z. (2012) A Novel Graphical Representation of Proteins and Its Application. Physica A: Statistical Mechanics and Its Applications, 391, 93-99.
- 33. Randic, M., Novic, M. and Vracko, M. (2008) On Novel Representation of Proteins Based on Amino Acid Adjacency Matrix. SAR and QSAR in Environmental Research, 19, 339-349.
http://dx.doi.org/10.1080/10629360802085082 - 34. Randic, M., Zupan, J. and Balaban, A.T. (2004) Unique Graphical Representation of Protein Sequences Based on Nucleotide Triplet Codons. Chemical Physics Letters, 397, 247-252.
http://dx.doi.org/10.1016/j.cplett.2004.08.118 - 35. Yao, Y.-H., Kong, F., Dai, Q. and He, P.-A. (2013) A Sequence-Segmented Method Applied to the Similarity Analysis of Long Protein Sequence. MATCH: Communications in Mathematical and in Computer Chemistry, 70, 431-450.
- 36. Abo-Elkhier, M.M. (2012) Similarity/Dissimilarity Analysis of Protein Sequences Using the Spatial Median as a Descriptor. Journal of Biophysical Chemistry, 3, 142-148. http://dx.doi.org/10.4236/jbpc.2012.32016
- 37. El-Lakkani, A. and El-Sherif, S. (2013) Similarity Analysis of Protein Sequences Based on 2D and 3D Amino Acid Adjacency Matrices. Chemical Physics Letters, 590, 192-195.
http://dx.doi.org/10.1016/j.cplett.2013.10.032 - 38. Abo el Maaty, M.I., Abo-Elkhier, M.M. and Abd Elwahaab, M.A. (2010) 3D Graphical Representation of Protein Sequences and Their Statistical Characterization. Physica A: Statistical Mechanics and Its Applications, 389, 4668-4676. http://dx.doi.org/10.1016/j.physa.2010.06.031
- 39. Wang, L., Peng, H. and Zheng, J.H. (2014) ADLD: A Novel Graphical Representation of Protein Sequences and Its Application. Computational and Mathematical Methods in Medicine, 2014, Article ID: 959753.
- 40. Balsera, M.A., Wriggers, W., Oono, Y. and Schulten, K. (1996) Principal Component Analysis and Long Time Protein Dynamics. Journal of Physical Chemistry, 100, 2567-2572.
- 41. Hess, B. (2000) Similarities between Principal Components of Protein Dynamics and Random Diffusion. Physical Review E—Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 62, 8438-8448. http://dx.doi.org/10.1103/PhysRevE.62.8438
- 42. Tournier, A.L. and Smith, J.C. (2003) Principal Components of the Protein Dynamical Transition. Physical Review Letters, 91, Article ID: 208106. http://dx.doi.org/10.1103/PhysRevLett.91.208106
- 43. Feng, Z.-P. and Zhang, C.-T. (2002) A Graphic Representation of Protein Sequence and Predicting the Sub-Cellular Locations of Prokaryotic Proteins. International Journal of Biochemistry and Cell Biology, 34, 298-307. http://dx.doi.org/10.1016/S1357-2725(01)00121-2
- 44. Randic, M. (2000) On Characterization of DNA Primary Sequences by a Condensed Matrix. Chemical Physics Letters, 317, 29-34.





