Received 15 January 2014; revised 7 February 2014; accepted 1 March 2014

ABSTRACT

This paper designs methods of product differences testing and preference testing by using triangle taste tests data. Binomial distribution theory and hypothesis test method are employed since that the existing statistical inference methods of triangle taste tests methods for sensory and quality analysis of cigarette products have some shortcomings. Finally, two case studies are provided, which have very important managerial implication to cigarette enterprises.

Keywords:

Binomial Distribution; Hypothesis Test; Triangle Taste Tests; Sensory and Quality

1. Introduction

The triangle taste tests method is used primarily for “difference testing”. It is one of the most important methods of sensory and quality evaluation of cigarette smoke product for cigarette manufacturers. These tests assist in evaluating effects of development in formulating products and processing. The principle for triangle taste tests method is that the assessors are presented with three products, two of which are identical and the other one is different. The assessors are asked to state which product they believe is the odd one.

^*Corresponding author.

Through field investigation on affiliates of Hongyun Honghe Tobacco Group, it is founded that the triangle taste tests have been widely adopted by cigarette manufacturers, but within an incorrect way from a statistical view. When the cigarette manufacturers deduce the sensory and quality of their products by using triangle taste tests data, most of them suffer mistakes. They use sample directly instead of population according to the plurality rule which is insufficiency in statistical inference process and statistical methods supporting, therefore unscientific judgments have been made on cigarette product quality judgment and lead to unscientific management decisions. This kind of problems not only exists in triangle taste tests for products sensory and quality analysis, but also in evaluation of quality control activities.

The authors did a comprehensive overview about statistical inference methods of using triangle taste test data through the National Knowledge Infrastructure(CNKI) database, but found few literature in China. The objects of this paper are to complement this gap and focus on the research of statistical inference methods based on mathematical statistics theory by using triangle taste tests data. This paper is organized as: Section 2 is methods design of statistical inference, and methods design for difference and goodness test for product sensory and quality which is based on Binomial distribution theory. Section 3 is case study, taking the Qujing cigarette manufacturer as an example. Section 4 is conclusions.

2. Methods Design of Statistical Inference

2.1. Introduction for Applications of Triangle Taste Tests

Within the triangle taste tests method for cigarettes products, firstly no less than 7 assessors grouped randomly, then a series of three kinds of cigarettes products which two are identical and the other one is different are presented to the assessors. The assessors are asked to identify which one is different from the other two and compare the sensory and quality of these products. Then the triangle taste tests data are collected and analyzed to make contribution to making decisions by the cigarette manufacturers. Obviously, this is a process of statistical decision based on small simple data.

2.2. Introduction of Mathematical Statistics Theory of Binomial Distribution

In mathematical statistics, the binomial distribution is the discrete probability distribution of the number of successes in a sequence of n independent yes or no experiments, each of which yields success with probability p [1] . Such a success/failure experiment is also called a Bernoulli experiment or a Bernoulli trial; when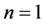, the binomial distribution is a Bernoulli distribution.

Binomial distribution describes the behavior of a count variable 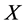if the following conditions apply:

1) The number of observations of 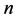is fixed.

2) Each observation is independent.

3) Each observation represents one of two outcomes (yes or no).

4) The probability of yes 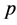is the same for each outcome.

If these conditions are met, then 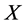has a Binomial distribution with parameters 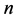and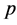, abbreviated 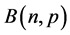[2] [3] .

2.3. Test Method for Products Quality Difference Based on Triangle Taste Tests

Take the detecting results of each assessor as a random collectivity and denoted by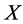. Each assessor is assumed to have a probability 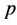of truly detecting the odd one product that is different from the other two identical products when 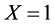(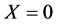, otherwise). According to the above section of definition of Bernoulli distribution and Binomial distribution, it is not hard to understand that 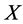followed the Bernoulli distribution.

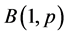Note that, if the assessor cannot identify the sensory and quality difference of the products caused by process adjustment, the process of truly detecting the odd one product is equiprobable and random, which means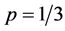, otherwise.

Therefore, whether the sensory and quality difference of the products caused by process adjustment could be tested as the following hypothesis testing:

(1)

Suppose there are assessors take part in triangle taste tests, the taste results for each assessor is an independent sample and denoted as. For each independent, it comes from population and followed by the same distribution of as. The sample value for is denoted as.

The rejection region of hypothesis testing Equation (1) is, where is the critical value. If the null hypothesis is true, the probability for rejection is, where is significance level. The level is the probability of rejecting the null hypothesis when it is true (type I error).

In order to show the magnitude of the significant level of the tests results, we calculate the p-value of the critical value instead of. The null hypothesis is rejected if the p-value turns out to be less than a certain significance level, often 0.05 or 0.01. Such a result indicates that the observed result would be highly unlikely under the null hypothesis (that is, the observation is highly unlikely to be the result of random chance alone).

Note that, the test statistics is, according to the above section of definition of Bernoulli distribution and Binomial distribution, it is not hard to understand that followed the Binomial distribution, if the null hypothesis is true, it changes to, therefore the p-value for testing is:

, where followed by Binomial distribution.

2.4. Preference Testing Method for Products Quality Based on Triangle Taste Tests

Take the detecting results of each assessor who can identify the sensory and quality difference of the products as a random collectivity and denoted by with, where for sensory and quality of the product is better if a special process adjustment is adopted, say process-A (, otherwise). is the probability when. Testing of whether the sensory and quality of the products is improved by adopting process-A is equivalent testing:

(2)

Note that, this part of this paper just focus on these assessors who can identify the sensory and quality difference of the products after process has been adjusted. That means we only observe the combined number of correct responses due to detection and guessing. The correct evaluation results are denoted as and values are.

The rejection region for the null hypothesis Equation (2) is, where is the critical value. The probability of rejection is if the null hypothesis is true, where is significance level. The equivalent testing method of its p-value also could be used.

The test statistics is with when.

Since, then the p-value is, where followed by Binomial distribution.

In addition, preference testing for two different kinds of products after process adjustment could be reached through the following two sides test:

(3)

where, the rejection region is or, and and are critical values. The probability of rejection is if the null hypothesis is true, where is significance level.

3. Case Study

3.1. Data Description

Qujing tobacco factory employed triangle taste tests to test sensory and quality of Brand-X and Brand-Y which were produced by different production technology in 2013 and 20 assessors were involved in total for each brand. Brand-X can be further divided as Sample-1 and Sample-2. These two samples were made of the same raw material but differed from process-A and process-B respectively with little adjustment. For Brand-X, the triangle taste tests statistical results showed that, 10 assessors detected the odd one cigarette from the other two identical cigarettes. Furthermore, 6 assessors preferred process-A cigarettes and the other 4 assessors preferred process-B cigarettes. Similarly, Brand-Y can be further divided as Sample-3 and Sample-4. These two samples were also made of the same raw material but differed from process-A and process-B respectively with little adjustment. For Brand-Y, the triangle taste tests statistical results showed that, 11 assessors detected the odd one cigarette from the other two identical cigarettes. Furthermore, 4 assessors preferred process-A cigarettes and the other 7 assessors preferred process-B cigarettes. The following Table 1 shows the original triangle taste tests data.

3.2. Results and Analysis of Statistical Inference

Based on the above sample data, what usually Qujing tobacco factory concluded were: 1) for Brand-X, there was no difference between process-A and process-B, since half of the assessors (10 assessors out of 20) detected the odd one cigarette from the other two identical cigarettes, they believed there were existing sensory and quality differences but the other half hold the opposite opinion. 2) for Brand-Y, there existed difference between process-A and process-B and process-B was better than process-A, since more than half of the assessors (11 assessors out of 20) detected the odd one cigarette from the other two identical cigarettes, moreover more than half of these assessors (7 assessors out of 11) prefer to process-B. Did the conclusions correct? The alternative analysis is showed as the following:

1) Does the products sensory and quality difference deduced from process adjustment?

According to Section 2.2, calculations are as the following:

a) For Brand-X, the p-value for testing is:

b) For Brand-Y, the p-value for testing is:

It is easy to understand that, for Brand-X and Brand-Y cigarette, process adjustment could give rise to differences of sensory and quality of the products, if the significance level is 0.1 (incorrect rejection of a true null hypothesis of indifference of sensory and quality of products). If the significance level is 0.05, for Brand-X, the null hypothesis of indifference of sensory and quality of products could not be rejected, since the p-value is 0.0919 and. But for Brand-Y, the null hypothesis of indifference of sensory and quality of products could be rejected, since the p-value is 0.0376 and.

Note: 1) “1”―correct detection; “0”—incorrect detection; 2) “A” process-A cigarettes have been preferred; “B” process-B cigarettes have been preferred.

2) Which process makes cigarette product better?

According to Section 2.3, calculations are as the following:

a) For Brand-X, the p-value for testing is:

b) For Brand-Y, the p-value for testing is:

These two p-values show that, for both Brand-X and Brand-Y cigarette, the null hypothesis of without improvements in the sensory and quality of the products by adopting process-A cannot be rejected, in spite of relaxation of the significance level to 0.1 even 0.3.

Furthermore, as mentioned before, preference testing for two different kinds of products after by using process-A and process-B could be reached through two sides test:

a) For Brand-X, the p-value for testing is:

where, where followed by Binomial distribution.

b) For Brand-Y, the p-value for testing is:

where, where followed by Binomial distribution.

The above p-values show that, for both Brand-X and Brand-Y cigarette, there is no obvious preference to either products of process-A adjustment or process-B adjustment, in spite of relaxation of the significance level to 0.1 even 0.5. This is equal to say, there is no significant evidence to show that the assessors have any preferences to the products which adjusted by process-A or process-B even if they can detect the differences of sensory and quality.

3) Comparison of analysis results

All the above analysis by using Binomial distribution theory and hypothesis test method concluded differently compared with the cigarette manufacturers. Table 2 shows the differences.

4. Conclusion

Triangle taste tests method had been applied widely in cigarette enterprises for products sensory and quality analysis. But they did not make full use of the triangle taste tests data in an inadequate way. Therefore, there wasn’t enough evidence to prove their inferences, which was not good for making scientific decisions. In this paper, methods of product differences testing and preference testing for products sensory and quality analysis were de-

signed based on Binomial distribution theory and hypothesis test method. Moreover, two case studies were given for the sake of providing important managerial implication to cigarette enterprises.

References