Journal of Electronics Cooling and Thermal Control
Vol.05 No.02(2015), Article ID:57409,17 pages
10.4236/jectc.2015.52003
CFD Study of Forced Air Cooling and Windage Losses in a High Speed Electric Motor
Kevin R. Anderson1, Jun Lin1, Chris McNamara1, Valerio Magri2
1California State Polytechnic University at Pomona: Mechanical Engineering, Pomona, USA
2CD-Adapco, Irvine, USA
Email: kranderson1@cpp.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 March 2015; accepted 22 June 2015; published 25 June 2015
ABSTRACT
High speed and high efficiency synchronized electric motors are favored in the automotive industry and turbo machinery industry worldwide because of the demands placed on efficiency. Herein an electric motor thermal control system using cooling air which enters from the drive end of the motor and exits from the non-drive end of the motor as the rotor experiences dissipates heat is addressed using CFD. Analyses using CFD can help to find the appropriate mass flow rate and wind- age losses while satisfying temperature requirements on the motor. Here, the air flow through a small annular gap is fed at 620 L/min (0.011 kg/sec) as the rotor spins at 100,000 rpm (10,472 rad/sec) and the rotor dissipates 200 W. The CFD results are compared with experimental results. Based upon the CFD findings, a novel heat transfer correlation suitable for large axial Reynolds number, large Taylor number, small annular gap Taylor-Couette flows subject to axial cross-flow is proposed herein.
Keywords:
Electronics Cooling, High-Speed Motor, Windage Losses, Conjugate Heat Transfer

1. Introduction
Due to demands placed on efficiency, high speed and high efficiency synchronized electric motors are favored in the automotive industry and turbo machinery industry worldwide. In general, direct coupling the electric motor to the drive shaft will yield simplicity of the mechanical design and deliver high system efficiency. However, the demand of high rotational speeds and high efficiencies can sometimes present difficulties when the RPM reaches 30,000 RPM to 100,000 RPM. The drag created in the air gap between the rotor and stator can result in significant “windage” losses that impact efficiency and increase motor cooling requirements. In some applications involving high power density electric motors forced air cooling is used to cool the rotor. The high rotational speed combined with the cooling air that travels in the axial direction creates very complex fluid dynamic flow profiles with coupled heat transfer and mass transfer. The relationship between the amount of the cooling air flow, windage generation and maximum temperature which the rotor can sustain is one of the most important factors in high speed electric motor design. Computational Fluid Dynamics (CFD) analysis must be performed to ensure proper cooling with low windage losses in order to achieve high efficiencies. Windage is a force created on an object by friction when there is relative movement between air and the object. There are two causes of windage: the first type is when the object is moving and being slowed by resistance from the air and the second type is where a wind is blowing producing a force on the object. The term windage can refer to: the effect of the force, for example the deflection of a missile or an aircraft by a cross wind or the area and shape of the object that make it susceptible to friction, for example those parts of a boat that are exposed to the wind. As shown in Figure 1 cooling air enters from the drive end of the motor and exits from the non-drive end of the motor. The heat transfer path is shown in Figure 1, whereby cooling air will pass through an air gap between the stator and the rotor where the rotor spins at 50,000 RPM to 100,000 RPM. Simultaneously, the rotor experiences electro-magnetic losses and dissipates heat.
As outlined above, in high-speed electronic motors air cooling is often employed in order to maintain the device within acceptable temperature operational limits. To date several investigations have been carried out on this topic. The pioneering work of Gardiner and Sabersky [1] showed that the experimental research on heat transfer within the annular gap of two cylinders could provide the basis for the design of the cooling system of high-power electric motors. The work of Haddadi and Poncet [2] considers the numerical modeling of the turbulent flow inside a rotor-cavity subjected to superimposed through flow, of Taylor-Couette-Poiseuille flow where rotational Reynolds numbers in the range of 105 < Re < 107 are considered and it is found that the inflow enhances the turbulence. In the research of Poncet and Schiestel [3] , numerical modeling of heat transfer and fluid flow in rotor-stator cavities with through flow is presented whereby a low Reynolds number second-order transport closure model is compared with empirical data where Nusselt number correlations are given for 5 ´ 105 < Re < 1.44 ´ 106 . From the study of Poncet et al. [4] , the turbulent flows in a differentially heated Taylor- Couette system with an axial Poiseuille flow. The numerical approach is based on the Reynolds Stress Modeling (RSM) where correlations for the averaged Nusselt numbers along both cylinders are finally provided according to the flow control parameters Reynolds number, friction coefficient and Prandtl number. In the work of Poncet et al. [5] Large Eddy Simulations of Taylor-Couette-Poiseuille flows in a narrow gap system are presented
Figure 1. High-speed electric motor cutaway view showing heat transfer cooling path.
together with a correlation for the Nusselt number along the rotor which shows a much larger dependence on the axial Reynolds number than expected from previous published works, while it depends classically on the Taylor number to the power 0.145 and on the Prandtl number to the power 0.3 i.e. Nu-Ta0.145Pr0.3. The work of Kuosa et al. [6] considers the numerical and experimental modeling of gas flow and heat transfer in the air gap of an electric machine where heat transfer coefficients are presented for the rotational speed range of 10,000 < n < 40,000 rpm. In the work of Murata and Iwamoto [7] heat and fluid flow in cylindrical and conical annular flow passages with through flow and inner wall rotation is numerically simulated by using the large eddy simulation with a Lagrangian dynamic subgrid-scale model. Inlet through-flow Reynolds number was Re = 1000 and the Taylor number was set at Ta = 0, 1000, 2000, and 4000. In the conical flow passage, when the inner-wall rotation speed was increased, at first spiral vortices in the downstream region and then much more complicated vortices appeared. The vortices for Ta = 4000 changed the structure in both through-flow and wall-normal directions in the downstream half of the passage. The flow structure and heat transfer of the conical case were completely different from those of the cylindrical case. The work of Jeng et al. [8] presents heat transfer enhancement of Taylor- Couette-Poiseuille flow in an annulus by mounting longitudinal ribs on the rotating inner cylinder. The work of Dubrille and Hersant [9] presents a summary of torque scaling in Taylor-Couette flow comparing numerical and experimental data showing that the large Taylor number large Reynolds number regime of flow gives a linear correlation between torque and Reynolds number. Hwang and Yang [10] present a numerical study of the Taylor-Couette flow with axial flow indicating that the axial flow stabilizes the flow field and decreases the torque required by rotating the inner cylinder at a given speed. The study of Fenot et al. [11] presents a comprehensive overview of heat transfer between concentric rotating cylinders subject to axial flow. The study of Fenot et al. [11] affords a summary of proposed heat transfer Nusselt number correlations for the Taylor-Couette-Poiseuille flow scenario. The experimental study of Tzeng [12] presents heat transfer in small gap between co-axial rotating cylinder and affords a correlation of the form Nu = 8.854Pr0.4Re0.262 1,000 < Re < 100,000 and 100 < Nu < 1.000. The work of Seghir-Ouali et al. [13] propose a correlation 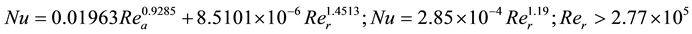 for the range 10,000 < Rer < 100,000 100 < Nu < 1000. The current study extends the previous studies into the realm of very large Taylor numbers, large axial Reynolds numbers, and small annular gap distances. The small annular gap is fed at 0.011 kg/sec while the rotor spins at 100,000 rpm while dissipating 200 W. The major objective of this present CFD analysis was to ascertain the drag force acting on the rotor of the motor. Comparisons of experimental power and numerical predictions are used to correlate the CFD model. One particular unique contribution of the present work is the extension of the current database of literature for Nusselt number and heat transfer coefficient into the Taylor/Reynolds number parameter space Ta > 108/Re > 104 range of turbulent flow with coherent vortex structures and heat transfer.
for the range 10,000 < Rer < 100,000 100 < Nu < 1000. The current study extends the previous studies into the realm of very large Taylor numbers, large axial Reynolds numbers, and small annular gap distances. The small annular gap is fed at 0.011 kg/sec while the rotor spins at 100,000 rpm while dissipating 200 W. The major objective of this present CFD analysis was to ascertain the drag force acting on the rotor of the motor. Comparisons of experimental power and numerical predictions are used to correlate the CFD model. One particular unique contribution of the present work is the extension of the current database of literature for Nusselt number and heat transfer coefficient into the Taylor/Reynolds number parameter space Ta > 108/Re > 104 range of turbulent flow with coherent vortex structures and heat transfer.
2. Methodology
2.1. Geometry and Boundary Conditions
Figure 1 shows the geometry of the high speed electric motor being studied herein. The motor consists of a stator, rotor, bearings, and an annular gap where air is fed to cool the motor. The rotor is a permanent magnet enclosed in an Inconel case. Figure 2 shows the boundary conditions used in the simulations. As shown in Figure 2, the air flow supply enters the annulus at a prescribed flow rate and temperature. The cooling air exits the annulus with a zero pressure boundary condition prescribed on the exit flow passage. As the motor spins, a rotating region in the STAR CCM + CFD model allows the user to prescribe the rotational speed of the rotor in order to mimic the motion of the fluid. Driven by design requirements, an upper limit is placed on the maximum temperature of the stator and rotor. For the purposes of simulating the conjugate heat transfer, the system has prescribed temperatures along the outer wall of the stator which are held at 150˚C. The internal dissipation of the motor is modeled by prescribing 200 W of internal heat dissipation in the main body of the rotor assembly. This value of internal heat dissipation was chosen to mimic the internal dissipation produced by the electric motor when operating. The primary objective of this CFD study was to quantify the amount of power dissipation in the rotor as the speed of the motor was varied. The nominal flowrate of air at 22˚C and 0.011 kg/sec was dictated by system components which interfaced with the motor. This data is useful to allow the further optimization of the high-speed motor.
Figure 2. Geometry and boundary conditions.
2.2. Governing Equations
The governing equations solved in STAR-CCM+ [14] via the Finite Volume Method for turbulent, conjugate heat transfer simulations are the incompressible, Navier-Stokes equations for Newtonian flow summarized below
 (1)
(1)
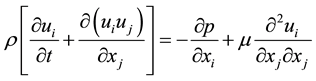 (2)
(2)
where 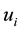 is the velocity component of the fluid in the
is the velocity component of the fluid in the 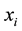 direction, p is the static pressure, m is the fluid viscosity. The Reynolds Averaged Navier Stokes (RANS) equations are obtained by applying the time averaging operation on Equation (1) and Equation (2) affording
direction, p is the static pressure, m is the fluid viscosity. The Reynolds Averaged Navier Stokes (RANS) equations are obtained by applying the time averaging operation on Equation (1) and Equation (2) affording
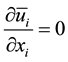 (3)
(3)
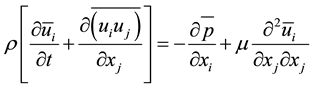 (4)
(4)
where 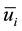 is the time averaged velocity component of the fluid in the
is the time averaged velocity component of the fluid in the 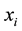 direction, while
direction, while 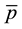 and r denote the time averaged pressure and density. Using the eddy viscosity approximation Equation. (4) is simplified for the steady mean field as follows
and r denote the time averaged pressure and density. Using the eddy viscosity approximation Equation. (4) is simplified for the steady mean field as follows
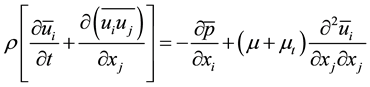 (5)
(5)
where 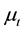 is the turbulent viscosity which is found via the particular turbulence model being employed. The thermal equation of state used herein was the ideal gas law. The constitutive equation modeling heat conduction in the solid bodies is taken to by Fourier’s Law. CD-Adapco’s STAR CCM+ Version 9.06 CFD software [14] was used to apply finite volume discretization of the above equations using implicit, unsteady, first order differencing implemented on an unstructured polyhedral mesh and the SIMPLE method of Patankar [15] for solving the coupled non-linear equations of motion. The resulting algebraic equations are solved using the Algebraic Multi-Grid method (AMG) at each time step. Due the incompressible nature of the flow (Ma < 0.3) the segregated flow and energy solver of STAR CCM+ was employed to enhance the solution process. Figure 3 shows the computational mesh used for the CFD simulations. The fluid mesh consisted of approximated 765,000 polyhedral cells, and the solids comprised approximately 559,000 polyhedral cells. The thin shell embedded meshing capabilities of STAR CCM+ were used to properly mesh the very thin annular gap region of the geometry. Typically in small aspect ratio channel flows, viscous heating effects become a concern, as in the work of Anderson [16] wherein liquid nitrogen is used in cooling channels to cool a rocket engine nozzle. The metric which determines if viscous heating is significant is the Brinkman number [17] , which was found to be on the order of unity, thus viscous heating effects are not considered to be profound in this current investigation.
is the turbulent viscosity which is found via the particular turbulence model being employed. The thermal equation of state used herein was the ideal gas law. The constitutive equation modeling heat conduction in the solid bodies is taken to by Fourier’s Law. CD-Adapco’s STAR CCM+ Version 9.06 CFD software [14] was used to apply finite volume discretization of the above equations using implicit, unsteady, first order differencing implemented on an unstructured polyhedral mesh and the SIMPLE method of Patankar [15] for solving the coupled non-linear equations of motion. The resulting algebraic equations are solved using the Algebraic Multi-Grid method (AMG) at each time step. Due the incompressible nature of the flow (Ma < 0.3) the segregated flow and energy solver of STAR CCM+ was employed to enhance the solution process. Figure 3 shows the computational mesh used for the CFD simulations. The fluid mesh consisted of approximated 765,000 polyhedral cells, and the solids comprised approximately 559,000 polyhedral cells. The thin shell embedded meshing capabilities of STAR CCM+ were used to properly mesh the very thin annular gap region of the geometry. Typically in small aspect ratio channel flows, viscous heating effects become a concern, as in the work of Anderson [16] wherein liquid nitrogen is used in cooling channels to cool a rocket engine nozzle. The metric which determines if viscous heating is significant is the Brinkman number [17] , which was found to be on the order of unity, thus viscous heating effects are not considered to be profound in this current investigation.
2.3. Turbulence Modeling
The k-w SST turbulence model of Wilcox [18] , Menter [19] is used as the closure model for the turbulent flow simulations presented herein. The k-w SST turbulence model is essentially the standard k-w turbulence model in the fully turbulent region far from the wall and the k-w turbulence model in the near wall region. According to the review of turbulence models given by Versteeg and Malalasekera [20] , the k-w SST turbulence model is particularly well suited for the narrow gap annulus cross-flow superimposed high swirl rotational flow scenario considered herein. The parameter w which is referred to as the turbulence frequency, having units of (1/sec) replaces the variable e in the standard k-e turbulence model as follows
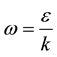 (6)
(6)
where k denotes the turbulent kinetic energy and e denotes the rate of dissipation of turbulent kinetic energy.
The turbulent viscosity is modeled as
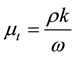 (7)
(7)
with the turbulence mixing length scale given by


Figure 3. CFD mesh in neighborhood of small annual gap.
The CD-Adapco STAR-CCM+ CFD code uses the following transport equations for the k-w SST high Reynolds number flow turbulence model

where

and the evolution equation for w reads

where the last term in Equation (12) is due to cross-diffusion. The model k-w SST constants are given by

A wall function based CFD turbulent simulation typically requires that y+ of the first cell outside of the wall lies in the log-layer, which starts at approximately y+ = 20 and depending on the Reynolds number extends to about y+ = 200. In the log-layer, there is equilibrium between production and dissipation of the turbulent kinetic energy, thus decreasing turbulent instability in near-wall simulations. The wall-treatments available in STAR CCM+ include, high-y+, low-y+ and all-y+. The all y+ wall treatment makes no assumption about how well the viscous sub layer is resolved. By using a blended wall log law of the wall to approximate the shear stress, the result is similar to the low y+ wall treatment if the mesh is fine enough. If the mesh is coarse enough, y+ > 30 the wall law is equivalent to a logarithmic profile. The all-y+ wall treatment is a hybrid method which attempts to emulate the high-y+ wall treatment for coarse meshes and the low-y+ wall treatment for fine meshes.
At the wall, a Neumann boundary condition is employed for the turbulent kinetic energy, k, i.e. ¶k/¶n = 0 at the wall. The specific dissipation rate w is prescribed in the wall cells according to the wall treatment being employed. When defining values for flow boundaries, region and initial conditions, the STAR CCM+ code allows users to 1) enter the values of k, w directly or 2) allows the CFD code to derive them from the turbulence intensity and length scale using


where u'/U is the turbulence intensity, Vt is the turbulent velocity scale and b* is a turbulent model constant.
2.4. Experimental Set-Up and CFD Model Correlation
The experimental test set-up is shown schematically in Figure 4 and a picture of the actualtest stand is shown in Figure 5. Figure 4 shows the electric motor under test with instrumentation for the air flow mass flow meter and the Variable Frequency Drive (VFD) to control the speed of the motor. Figure 5 shows the standalone test setup showing the motor on the test stand. The two small blue hoses on top of the motor are for water in and water out. The black hose on the lower right side of the motor is for the supply air in. There is a mass flow meter that measuring the air inlet mass flow rate (not pictured in Figure 5, but shown schematically in Figure 4 and there is a K-type thermocouple measuring the air temperature just before the air enters to the motor). Also shown in Figure 5 is the air outlet to the ambient exiting on the upper left hand side on the motor. The larger diameter blue hoses on the left hand side of the test stand in Figure 5 are for the coolant oil inlet and outlet for the bearing lubrication system. The test stand of Figure 5 was used to generate the data of Table 1. The data of Table 1 is in qualitative agreement with the data presented by Kuosa et al. [6] for their stator and rotor temperatures
Figure 4. Block diagram of experimental apparatus.
Figure 5. Experimental apparatus.
Table 1. Experimental and CFD windage power results comparison.
a. Inlet air flow rate = 620 L/min at T = 21.5˚C.
at similar rotational speeds and air flowrates albeit for a larger gap size then addressed herein. Table 1 shows the speed of the motor, the air inlet temperature to the motor, the air outlet temperature from the motor, and the computed air energy based on the following relationship

as compared to the same parameters from the CFD model. The last column of Table 1 lists the percentage error between the empirically determined air power versus that predicted by the CFD model. The error in Table 1 is on the order of 19% which is consistent with having a conservative CFD model which tends to over-predict the energy losses in the system. The data in Table 1 were gathered by allowing the air outlet temperature to stabilize at each rotational speed setting, n (rpm). The water entering the system varied from 35.8˚C to 41˚C. This was done to minimize the heat transfer from the air to the water. The test results of Table 1 for inlet to outlet temperature rise are in qualitative agreement with those presented by Kuosa et al. [6] . Figure 6 is included to show the expected cubic dependency of power on the speed, P-n3. Figure 6 shows the data of Table 1 plotted for both the empirical measurements as well as the CFD results. Both trend-lines for CFD and experimental data are seen to be cubic and the correlation coefficient is R2 = 0.9995 for the CFD data and R2 = 0.9997 for the empirical data. Figure 6 shows that the CFD model is correlated to the test data.
3. Results and Discussion
In this section the results of the CFD study are given. First the fluid mechanics of the small annulus flows considered herein are compared with existing literature. Then, heat transfer analysis using the CFD results is given. Finally, a Nusselt number based on the findings of the present research is proposed.
3.1. Effect of Inlet Air Flow Rate on Flow Structures
The flow structures shown in Figure 7 and Figure 8 are of consistent pattern and content as those reported by Hwang and Yang [10] where the primary effect of the inlet Poiseuille flow is seen to “flatten” out the Taylor cells. This is witnessed by the somewhat square nature of the vortices shown in Figure 7 and Figure 8. The pairing of vortex structures shown in Figure 7 agrees with the predictions reported in Hwang and Yang [10] . When the axial flowrate is turned off, the cells begin to become more circular in structure, corresponding to Taylor-Couette flows. In order to assess the region of flow developed within the annular gap, Figure 9 adapted from Schlichting [21] is used to determine the nature of the Taylor-Couette-Poiseuille flow. Figure 9 can be viewed as a road map of annulus based Reynolds Number, Re = w2d/n versus Taylor number based on the inner diameter of the rotating cylinders
Figure 6. Experimental and CFD windage power loss comparison.
Figure 7. Taylor cells for Reaxial = 7.59 ´ 103, Ta = 3.24 ´ 108.
Figure 8. Taylor vortices for (a) No-axial inlet air cooling; (b) Moderate inlet air cooling.

as noted in Figure 9. Depending upon the Re/Ta combination the Taylor-Couette-Poiseuille flow is either (a) laminar, (b) laminar with Taylor vortices, (c) turbulent with vortices, or (d) turbulent flow. For the CFD simulations presented herein, the following geometric parameters per the development of Fenot et al. [11] were used: the inner cylinder radius, R1 = 24.78 mm, the outer cylinder radius, R2 = 27.89 mm, the annular gap thickness, e = R2 − R1 = 3.11 mm, the cylinder length, L = 98.54 mm, the radius ratio, h = R1/R2 = 0.888, the cylindrical gap ratio, f = e/R1 = 0.126, and the axial ratio, G = L/(R2 − R1) = 31.685. The cooling fluid was air at 22˚C, with a mass density of r = 1.16 kg/m3, specific heat ratio, Cp = 1011 J/kg×K, thermal conductivity, k = 0.0260 W/m∙K, kinematic viscosity, n = 1.51 ´ 10−5 m2/sec, mean rotor temperature, Tr = 112.5˚C, mean stator temperature, Ts = 130˚C. The results comparing the various correlations for Nusselt number listed in Table 2 employed an axial mass flow rate, 


Figure 9. Axial Reynolds number vs. Taylor number flow regime map [18] .
Table 2. Heat transfer correlation parameter comparison.
Number,
3.2. Non-Dimensional Torque
In order to compare the current data to other researchers including Sebastin and Egbers [22] , Merbold et al. [23] and van Gils et al. [24] , the non-dimensional torque versus the gap based Reynolds number was investigated. The non-dimensional torque, 


The data of Figure 12 is found to be in agreement with the findings of Dubrulle and Hersant [9] for Re > 107. It should be noted that the correlation presented herein as Equation (18) holds for Taylor-Couette-Poiseuille
Figure 10. Vorticity isosurfaces for Reaxial = 7.59 ´ 103, Ta = 3.24 ´ 108.
Figure 11. Velocity vectors for Reaxial = 7.59 ´ 103, Ta = 3.24 ´ 108.
flows, whereas the works of Dubrulle and Hersant [9] , Sebastin and Egbers [22] , Merbold et al. [23] and van Gils et al. [24] present data for Taylor-Couette flows. To the present author’s knowledge, no literature could be recovered for torque versus Reynolds number for Taylor-Couette-Poiseuille flow situation, thus the correlation proposed as Equation (18) appears to be warranted.
3.3. Heat Transfer Analysis
Figure 13 shows a cross-sectional view of the isotherms for the flow field. The top and bottom are held at 150˚C per the boundary conditions, while the inner section of the rotor has a 200 W dissipation prescribed. The flow enters the top left of Figure 13 and exits at the bottom right of Figure 13. The overall spatial temperature gradient is DT = 150˚C − 25˚C = 125˚C, while the local gradient experienced by the air is on the order of DT =
Figure 12. Non-dimensional torque vs. gap Reynolds number.
Figure 13. Tempeature isotherms for Reaxial = 7.59 ´ 103, Ta = 3.24 ´ 108.
88˚C − 25˚C = 63˚C which is consistent with the test data and CFD data of Table 1. From Figure 13, the radial temperature gradient across the annulus is approximately 127˚C − 105˚C = 22˚C. The local temperature in the Taylor-Couette-Poiseuille flows in the annulus ranges from 93˚C to 127˚C as a function of the downstream distance along the annulus. Thus the axial gradient in the annulus is on the order of 127˚C − 93˚C = 34˚C. Figure 14 shows the local heat transfer coefficient contours for the flow field ranging from 1456 < h < 6641 W/m2∙K. It should be noted the local heat transfer coefficient in Figure 14 is computed within the STAR CCM+ software as a post-processed (i.e. non-primitive) variable, where the heat transfer coefficient is proportional the local temperature gradient in the flow field, h ~ 1/¶T/¶n. For the purposes of post-processing the STAR-CCM+ software allows the user to prescribe the turbulent log-law-of-the-wall y+ value to be used to scale the ¶T/¶n gradient and thus produce the post-processing images. In unison with turbulence modeling practices Wilcox [18] , the value of y+ = 100 is typically accepted, as it corresponds to the linear region of the log-law-of-the wall. To this end, the specified y+ heat transfer coefficient contours of Figure 14 were generated, from whence the Nusselt number contour plots of Figure 15 were produced in STAR CCM+ using a field function in the format Nu = he/k, e = annulus gap distance. Figure 15 shows contours of the local Nusselt number in the range of 346 < Nu < 1580.
3.4. Nusselt Number Correlation Based on Present Study
The results of the present study for heat transfer coefficient and Nusselt number were compared to several previous studies where the rotor of the machine being studied was heated including the works of Childs and Turner [25] , Grosgeorge [26] , Kostein and Finat’ev [27] , Bouafia et al. [28] , Nijaguan and Mathiprakasm [29] , Hanagida and Kawasaki [30] , and Tachibana and Fukui [31] . Each of these investigations proposes a Nusselt number correlation for the Taylor-Couette-Poiseuille flow in a rotating machine. The details of the above referenced correlations are summarized in the comprehensive review of Fenot et al. [11] . Figure 16 is included herein in order to cast the correlation of interest in the proper realm of the Taylor-Couette-Poiseuille flow map. Following the work of Becker and Kaye [32] , the roadmap of Re versus Ta in Figure 16 is constructed with each of the correlations of above plotted in the Re/Ta parameter space. As seen in Figure 16, the majority or currently available correlations for heat transfer coefficient are fro Ta < 108, Re > 103. The majority of correlations with which our current data was compared against lie within the “turbulent and vortices” region of Taylor-Couette- Poiseuille flow, as shown in Figure 16. The unique contribution of the present work is the extension of the
Figure 14. Local heat transfer coefficient for Reaxial = 7.59 ´ 103, Ta = 3.24 ´ 108.
Figure 15. Local nusselt number contours for Reaxial = 7.59 ´ 103, Ta = 3.24 ´ 108.
Figure 16. Reynolds number and Taylor number for heat transfer correlations.
current database of literature into the large Ta > 108/Re > 104 range of turbulent flow with coherent vortices. The parameters used to compare our current work are summarized in Table 2. The various correlations cited above are compared to the current CFD simulation in Figure 17, where the heat transfer coefficient and Nusselt number for each correlation is shown in comparison with the present work. With respect to the other studies listed in Table 2, it can be seen that the present CFD simulations correspond to the second largest Taylor number, Ta = 3.24 ´ 108 and the smallest cylindrical gap ratio f = 0.0017. The correlation with the best agreement to our results which is in the same realm of Taylor numbers is that of Childs and Turner [25] where Ta = 1.2 ´ 1011 with a cylindrical gap ratio f = 0.15, i.e. two orders of magnitude larger than the current study. Nevertheless, the heat transfer coefficient of the current study h = 1800 W/m2・K vs. the value of h = 1329 W/m2・K of Childs and Turner [25] seems to be in qualitative agreement from an order of magnitude standpoint for the very large Taylor number regime of flows. Again, we should remind ourselves of the advice proposed by Incropera and Dewitt [33] in that these heat transfer correlation based on Nusselt numbers are by no means “sacrosanct”, and we should expect at the very minimum an uncertainty of ±20% on the mean value of the heat transfer coefficient. Recognizing the uniqueness of the Ta/f/Re combination of parameters we presently adders, we propose the Nusselt number versus Taylor number correlation shown in Figure 18, which affords Equation (19) as follows

with a stated correlation coefficient of R2 = 0.9713. The correlation of Equation (19) extends the findings of Poncet et al. [4] from their reported Nu vs. n (rpm) data, and agrees qualitatively with the research of Bouafia et al. [28] in the large Taylor number region of flow, Ta > 108. Thus, the correlation offered herein as Equation (19) addresses large Taylor-large axial Reynolds number-small gap, Taylor-Couette-Poiseuille flows with heat transfer.
4. Conclusion
This paper has presented the results of using the commercial Computational Fluid Dynamics (CFD) package STAR CCM+ to simulate air cooling and windage losses in a high-speed electric motor. The primary objective
Figure 17. Heat transfer correlations comparison.
Figure 18. Nusselt number correlation based on present CFD study.
of this CFD analysis was to ascertain the drag force acting on the rotor of the motor. This work is significant in that it provides designers of high-speed air cooled motors a means that can be used to quickly assess the impact of windage losses on motor thermal performance. The CFD results are found to match the empirical data to within 20%, thus affording a conservative, correlated CFD model. The local heat transfer coefficient contours for the flow field ranging from 1456 < h < 6641 W/m2×K, while the local Nusselt number falls in the range of 346 < Nu < 1580. A novel Nusselt number correlation based on the CFD results of this study is proposed in the form Nu = 1.5975Ta0.3282.
Acknowledgements
The authors would like to acknowledge Dr. Angela Shih, Mechanical Engineering Department Chair for support of this research.
References
- Gardiner, S. and Sabersky, R. (1977) Heat Transfer in an Annular Gap. International Journal of Heat and Mass Transfer, 21, 1459-1466. http://dx.doi.org/10.1016/0017-9310(78)90002-9
- Haddadi, S. and Poncet, S. (2008) Turbulence Modeling of Torsional Couette Flows. International Journal of Rotating Machinery, 2008, Article ID: 635138. http://dx.doi.org/10.1155/2008/635138
- Poncet, S. and Schiestel, R. (2007) Numerical Modeling of Heat Transfer and Fluid Flow in Rotor-Stator Cavities with Through Flow. International Journal of Heat and Mass Transfer, 50, 1528-1544. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2006.08.028
- Poncet, S., Haddadi, S. and Viazzo, S. (2011) Numerical Modeling of Fluid Flow and Heat Transfer in a Narrow Taylor-Couette-Poiseuille System. International Journal of Heat and Fluid Flow, 32, 128-144. http://dx.doi.org/10.1016/j.ijheatfluidflow.2010.08.003
- Poncet, S., Viazzo, S. and Oguic, R. (2014) Large Eddy Simulations of Taylor-Couette-Poiseuille Flows in a Narrow- Gap System. Physics of Fluids, 26, 105-108. http://dx.doi.org/10.1063/1.4899196
- Kuosa, M., Sallinen, P. and Larjola, J. (2004) Numerical and Experimental Modeling of Gas Flow and Heat Transfer in the Air Gap of an Electric Machine. Journal of Thermal Sciences, 13, 264-278. http://dx.doi.org/10.1007/s11630-004-0041-4
- Murata, A. and Iwamoto, K. (2011) Heat and Fluid Flow in Cylindrical and Conical Annular Flow-Passages with Through and Inner-Wall Rotation. International Journal of Heat and Fluid Flow, 32, 378-391. http://dx.doi.org/10.1016/j.ijheatfluidflow.2011.01.004
- Jeng, T.M., Tzeng, S.C. and Lin, C.H. (2007) Heat Transfer Enhancement of Taylor-Couette-Poiseuille Flow in an An- nulus by Mounting Longitudinal Ribs on the Rotating Inner Cylinder. International Journal of Heat and Mass Transfer, 50, 381-390. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2006.06.005
- Dubrulle, B. and Hersant, F. (2002) Momentum Transport and Torque Scaling in Taylor-Couette Flow from an Analogy with Turbulent Convection. The European Physical Journal B, 26, 379-386. http://dx.doi.org/10.1140/epjb/e20020103
- Hwang, J.Y. and Yang, K.S. (2004) Numerical Study of Taylor-Couette Flow with and Axial Flow. Computers & Fluids, 33, 97-118. http://dx.doi.org/10.1016/S0045-7930(03)00033-1
- Fenot, M., Bertin, Y., Dorignac, E. and Lalizel, G. (2011) A Review of Heat Transfer between Concentric Rotating Cy- linders with or without Axial Flow. International Journal of Thermal Sciences, 50, 1138-1155. http://dx.doi.org/10.1016/j.ijthermalsci.2011.02.013
- Tzeng, S.C. (2006) Heat Transfer Is a Small Gap between Co-Axial Rotating Cylinders. International Communications in Heat and Mass Transfer, 33, 737-743. http://dx.doi.org/10.1016/j.icheatmasstransfer.2006.02.012
- Seghir-Ouali, S., Saury, D., Harmand, S., Phillipart, O. and Laloy, D. (2006) Convective Heat Transfer inside a Rotating Cylinder with an Axial Air Flow. International Journal of Thermal Sciences, 45, 1166-1178. http://dx.doi.org/10.1016/j.ijthermalsci.2006.01.017
- STAR CCM+ Users Manual. http://www.cd-adapco.com/products/star-ccm/documentation
- Patankar, S. (1980) Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing Corporation, Washington DC and McGraw-Hill, New York.
- Anderson, K.R. (2004) CFD Analysis of Inlet and Outlet Regions of Coolant Channels in an Advanced Hydrocarbon Engine Nozzle. Proceedings of the 15th Annual Thermal and Fluids Analysis Workshop, TFAWS-04, Pasadena, 30 August-3 September 2004.
- White, F. (1974) Viscous Fluid Flow. McGraw Hill, New York.
- Wilcox, D. (1998) Turbulence Modeling for CFD. 2nd Edition, DCW Industries Inc., La Cañada Flintridge.
- Menter, F. (1994) Two Equation Eddy-Viscosity Turbulence Modeling for Engineering Applications. AIAA Journal, 32, 1598-1605. http://dx.doi.org/10.2514/3.12149
- Versteeg, H. and Malalasekera, W. (2007) An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Pearson Education Ltd., Harlow.
- Schlichting, H. (1935) Boundary Layer Theory. McGraw-Hill, New York.
- Sebastian, M. and Egbers, C. (2013) Torque Measurements in a Wide Gap Taylor-Couette Flow. 14th European Turbulence Conference, Lyon, 1-4 September 2013.
- Merbold, S., Brauckmann, H. and Egbers, C. (2013) Torque Measurements and Numerical Determination in Differentially Rotating Wide Gap Taylor-Couette Flow. Physical Review E, 87, Article ID: 023014. http://dx.doi.org/10.1103/PhysRevE.87.023014
- van Gils, D., Huisman, S., Bruggert, G.-W., Sun, C. and Lohse, D. (2011) Torque Scaling in Turbulent Taylor-Couette Flow with Co- and Counter-Rotating Cylinders. Physical Review Letters, 106, Article ID: 024502. http://dx.doi.org/10.1103/PhysRevLett.106.024502
- Childs, P. and Turner, A. (1994) Heat Transfer on the Surface of a Cylinder Rotating in an Annulus at High Axial and Rotational Reynolds Numbers. 10th International Heat Transfer Conference, Brighton, 13-18.
- Grosgeorge, M. (1983) Contribution a letude du refroidissement dune paroi tourante par air charge dhulle pulversdee. Thèses de doctorat, Université de Nacy.
- Kostein, L. and Finat’ev, Y. (1963) Investigation of Heat Transfer of a Turbulent Flow of Air in an Annular Gap between Rotating Coaxial Cylinders.
- Bouafia, M., Ziouchi, A., Bertin, Y. and Saulnier, J. (1999) Étude expérimentale et numérique des transferts de chaleur en espace annulaire sans débit axial et avec cylindre intérieur tournant. International Journal of Thermal Sciences, 38, 547-559. http://dx.doi.org/10.1016/S0035-3159(99)80035-X
- Nijaguna, B. and Mathiprakasam, B. (1982) Heat Transfer in an Annulus with Spiral Flow. 7th International Heat Transfer Conference, Munich.
- Hanagida, T. and Kawasaki, N. (1992) Pressure Drop and Heat Transfer Characteristics of Axial Air Flow through an Annulus with a Deep Slotted Outer Cylinder and a Rotating Inner Cylinder. Heat Transfer Japanese Research, 21, 292-304.
- Tachibana, F. and Fukui, S. (1964) Convective Heat Transfer of the Rotational and Axial Flow between Two Concentric Cylinders. Bulletin of JSME, 7, 385-391.
- Becker, K.M. and Kaye, J. (1962) The Influence of a Radial Temperature Gradient on the Instability of Fluid Flow in an Annulus with an Inner Rotating Cylinder. Transaction of ASME Journal of Heat Transfer, 82 106-110. http://dx.doi.org/10.1115/1.3684306
- Incropera, F. and De Witt, D. (1985) Introduction to Heat Transfer. Wiley, New York.




















