Journal of Electronics Cooling and Thermal Control
Vol.2 No.4(2012), Article ID:25313,4 pages DOI:10.4236/jectc.2012.24006
Effects of Baffle on Entropy Generation in Separated Convection Flow Adjacent to Inclined Backward-Facing Step
1Mechanical Engineering Department, School of Engineering, Shahid Bahonar University, Kerman, Iran
2Computer Department, Kerman Branch of Azad University, Kerman, Iran
Email: ganj110@uk.ac.ir
Received November 10, 2012; revised December 10, 2012; accepted December 17, 2012
Keywords: Entropy Generation; Inclined Backward Step; Baffle; Convection Flow
ABSTRACT
Numerical simulations of a two-dimensional laminar forced convection flow adjacent to inclined backward-facing step in a rectangular duct are presented to examine effects of baffle on flow, heat transfer and entropy generation distributions. The main aim of using baffles is to enhance the value of convection coefficient on the bottom wall. But the useful energy can be destroyed due to intrinsic irreversibilities in the flow by the baffle. In the present work, the amount of energy loss is estimated by the computation of entropy generation. The values of velocity and temperature which are the inputs of the entropy generation equation are obtained by the numerical solution of momentum and energy equations with blocked-off method using computational fluid dynamic technique. Discretized forms of the governing equations in the (x, y) plane are obtained by the control volume method and solved using the SIMPLE algorithm. Numerical expressions, in terms of Nusselt number, entropy generation number, Bejan number and coefficient of friction are derived in dimensionless form. Results show that although a baffle mounted onto the upper wall increases the magnitude of Nusselts number on the bottom wall, but a considerable increase in the amount of entropy generation number takes place because of this technique. For validation, the numerical results for the Nusselt number and entropy generation number are compared with theoretical findings by other investigators and reasonable agreement is found.
1. Introduction
Forced convection flows in channels with abrupt expansion or contraction are widely encountered in engineering applications, such as cooling passages of turbine blades, diffusers, combustors and heat exchangers. These separated flows are intrinsically irreversible because of viscous dissipation, reattachment and recirculation. The flow over backward facing step (BFS) was studied by several investigators both theoretically and experimentally to find the physics of such separated flows. Most of research works on BFS has been extensively carried out from fluid mechanics and heat transfer perspectives. Armaly et al. [1] analyzed laminar, transition, and turbulent isothermal flows over a BFS both experimentally and theoretically. Flow over a BFS with force convection heat transfer was conducted by other investigators by different numerical techniques [2-7]. These results showed that the flow separation and subsequent recirculation result in very poor heat transfer performance in the region near the backward facing step. A review of research on laminar mixed convection flow over forwardand backward-facing steps was done by Mulaweh [8].
The compactness of new thermal systems leads the importance of finding effective means for enhancing heat transfer. Using baffles is one of an effective method for this purpose. In a recent study by Nie et al. [9] about convection flow over BFS, it was revealed that a baffle mounted onto the upper wall increases considerably the magnitude of maximum Nusselt number at the stepped wall. In that study, the set of governing equations including continuity, momentum and energy equations for three-dimensional convection laminar flow over BFS in a duct were solve numerically by CFD technique. The effects of baffle location and its height on flow and heat transfer distributions were carried out.
Recently, entropy generation analysis has been extensively applied in many fluid flows with heat transfer in different geometries. Entropy generation analysis provides a useful tool to identify the irreversibilities in any thermal system as well as to determine the optimum condition for any process. Heat transfer and viscous dissipation are the only sources of entropy generation in force convection fluid flow. There are a few studies in which the analysis of entropy generation due to forced convective flow over a BFS has been conducted [10,11]. Recently, investigation of entropy generation in a flow over a BFS under bleeding condition was done by Abu-Nada [12]. In that work, the set of governing equations were solved by the finite volume method and the distributions of entropy generation number on solid surfaces at different conditions were calculated. Moreover, the effects of bleed coefficient for both blowing and suction on the entropy generation number and Bejan number were presented.
In the present work for the first time, the entropy generation analysis for convection flow over an inclined BFS in a duct with baffle is carried out. Considering inclined step makes the problem more general in comparison to the researches in all of the above references in which the step has right angle. The main aim is to identify the irreversibilities and entropy generation due to baffle against its advantage which is enhancing the convection coefficient in the thermal system. Toward this end, the set of governing equations consisting the conservation of mass, momentum and energy and also the entropy generation equation are solved by CFD method in the Cartezian coordinate system using blocked-off method. Finally, the effects of baffle location and its height on the distributions of Nusselt number, entropy generation number and friction coefficient are explored.
2. Theory
For calculating the amount of entropy generation in the force convection flow indicated in Figure 1, the velocity and temperature distributions are primary needed. For two-dimensional incompressible, steady and laminar flow, the non dimensional forms of the governing equations which are the conservations of mass, momentum and energy can be written as follows:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
in Equations (1) to (4), the following dimensionless groups are used:


where Pr and Re are the prandtl and Reynolds numbers, respectively and  is the characteristic length which is assumed to be the duct height after the step.
is the characteristic length which is assumed to be the duct height after the step.
2.1. Boundary Conditions
The boundary conditions for the hydrodynamic problem are impermeability and non-sliping on the solid boundaries including the baffle. Besides, at the inlet section, uniform flow with velocity V0 is considered and at the outlet section, zero axial gradients for velocity components are imposed.
In solving the energy equation, the surfaces of the top wall with the baffle and bottom wall including the step are considered isotherm with the constant temperatures  and
and , respectively. Besides, at the inlet section, a uniform temperature
, respectively. Besides, at the inlet section, a uniform temperature ![]() is assumed and at the outlet section, zero temperature gradient in x-direction is employed.
is assumed and at the outlet section, zero temperature gradient in x-direction is employed.
2.2. Regular Grid with Blocked-Off Region
We now describe the manner in which we treat the geometry of inclined step using the blocking-off method (Patanker [13]). By blocked-off technique, a CFD based computer program written for a regular grid can be improved to handle an irregularly shaped computational domain. This can be done by rendering inactive some of the control volumes of the regular grid so that the remaining active control volumes form the desired irregular domain with complex boundary. Example is shown in Figure 2, where the shaded areas denote the inactive control volumes. It is obvious that arbitrary geometries are approximated by a series of the rectangular grids. It is worth mentioning that using fine grids in the interface region between active and inactive zones causes to have an approximated boundary which is more similar to the true boundary.
Idea of the blocking-off operation consists of establishing known values of the relevant dependent variables in the inactive control volumes. If the inactive region represents a stationary solid zone as in the case, the velocity components in that region must be equal to zero, and if the region is regarded as isothermal one, the known temperature must be established in the inactive control volumes. In the present computations, zero velocity in the inactive zone is employed by use of a very large viscosity for grid points in that region with considering no slip condition on the nominal boundaries. In thermal problem, the nominal boundaries are considered isotherm and large value for thermal conductivity for the grid points inserted in the inactive zone is employed. By

Figure 1. Physical model.

Figure 2. Blocked-off region in a regular grid.
this technique, the grid points in the inactive zone become isotherm such that their temperatures are equal to the temperature considered on the nominal boundaries.
3. Entropy Generation
To analyze the entropy generation in forced flow problems, the analyzer needs to use equations from which the entropy generation can be calculated. These equations can be derived by identifying the sources of entropy generations and then applying the second law of thermodynamics. In the forced convection flow, the entropy generation is associated to the heat transfer and fluid flow friction. Bejan [14] derived the overall general entropy generation in Cartesian coordinate system as follows:
 (5)
(5)
the non dimensional form of this equation for calculating the entropy generation number is given as [12]:
 (6)
(6)
the following dimensionless quantities are defined:

where Ns is the entropy generation number,  the volume rate of entropy generation, Br the Brinkman number and τ is the non-dimensional temperature difference.
the volume rate of entropy generation, Br the Brinkman number and τ is the non-dimensional temperature difference.
In Equation (6), the first term represents entropy generation due to heat transfer ( ), while the second term represents the entropy generation due to the fluid viscous effect (
), while the second term represents the entropy generation due to the fluid viscous effect ( ). The Bejan number which is defined as follows is also computed in the present analysis.
). The Bejan number which is defined as follows is also computed in the present analysis.
 (7)
(7)
According to the definition of Bejan number, the irreversibilities due to the viscous effect are dominant when . When
. When , the heat transfer irreversibilities dominate the process and if Be = 0.5, the entropy generation due to the viscous effect and heat transfer are equal.
, the heat transfer irreversibilities dominate the process and if Be = 0.5, the entropy generation due to the viscous effect and heat transfer are equal.
4. Solution Strategy
In this section, a brief overview of the numerical method used for the solution of the governing equations is presented. Finite difference forms of the continuity, momentum and energy equations are obtained by integrating over an elemental cell volume with staggered control volumes for the xand yvelocity components. The discretized forms of the governing equations are numerically solved by the SIMPLE Algorithm of Patankar and Spalding [15] for the pressure correction in the iteration procedure. Numerical solutions of the governing equations together with the boundary conditions are obtained iteratively by the line-by-line method by utilizing the TriDiagonal-Matrix Algorithm (TDMA). Iterations are terminated when sum of the absolute residuals becomes less than  for each equation. As the result of grid tests for obtaining the grid-independent solutions, an optimum grid of 400
for each equation. As the result of grid tests for obtaining the grid-independent solutions, an optimum grid of 400  150 with clustering near the solid surfaces is determined in xand ydirections.
150 with clustering near the solid surfaces is determined in xand ydirections.
After calculation of velocity and temperature fields, Equation (6) is used to solve for the entropy generation number at each grid point in the flow domain. Then, the total entropy generation through the flow domain is calculated as:
 (8)
(8)
where V is the volume of computational domain. Also, the average Bejan number is also calculated by the following equation:

Besides, the distributions of friction coefficient and Nusselt number on the bottom wall are determined as follows:
 (9)
(9)
 (10)
(10)
5. Validation of Computational Results
The present numerical implementation is validated by reproducing the theoretical results of two other investigators. Along two different test cases, the results of Nusselt number in convection flow over BFS with baffle are compared with those presented by Nie et al. [9] and the results of entropy generation number with that of the Abu Nada [12]. In these two works, the BFS was considered to be vertical to the stepped wall. It should be noted that in solving the governing equations for these two test cases, the same values for parameters which were used in Refs. [9,12] are considered in the present analysis. Fiure 3 shows the variation of Nusselt number along the bottom wall. It is seen that the value of maximum Nusselt number increases due to baffle effect. For instance, the maximum Nusselt number for 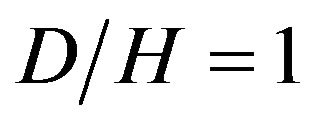 is about three times of the one for
is about three times of the one for 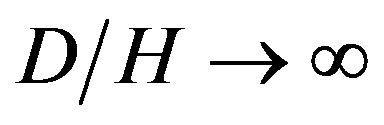 (without baffle). Also, the location of
(without baffle). Also, the location of 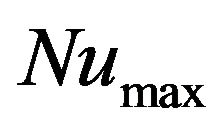 moves downstream as the baffle moves along the stream wise direction. For another test case in a convection flow over BFS without baffle, the variation of entropy generation number Ns along the bottom wall is shown in Figure 4. It is seen that the minimum value of Ns occurs directly at x = 0 at the bottom step corner, where the fluid has no motion. The maximum value of Ns takes place inside the recirculation zone and then it drops sharply to a very low value at the reattachment point after which Ns increases and approaches to a constant value far from the step. However Figures 3 and 4 show that the general agreements between the present results with the theoretical findings by other investigators are quite good and the values of minimum and maximum entropy generation numbers and Nusselt numbers and their predicted locations are reasonably closed to each other.
moves downstream as the baffle moves along the stream wise direction. For another test case in a convection flow over BFS without baffle, the variation of entropy generation number Ns along the bottom wall is shown in Figure 4. It is seen that the minimum value of Ns occurs directly at x = 0 at the bottom step corner, where the fluid has no motion. The maximum value of Ns takes place inside the recirculation zone and then it drops sharply to a very low value at the reattachment point after which Ns increases and approaches to a constant value far from the step. However Figures 3 and 4 show that the general agreements between the present results with the theoretical findings by other investigators are quite good and the values of minimum and maximum entropy generation numbers and Nusselt numbers and their predicted locations are reasonably closed to each other.
6. Results and Discussion
The entropy generation in convection laminar air flow over an inclined backward step in a duct with a baffle

Figure 3. Distribution of Nusselt number on the bottom wall at two different baffle locations, Re = 343, θ = 90˚.

Figure 4. Variation of entropy generation number along the bottom wall Re = 400, θ = 90˚.
mounted onto the upper wall is calculated for the purpose of determining the amount of irreversibilities due to baffle. Toward this end, the continuity, momentum and energy equations are solved numerically by CFD method. In the present computations for the physical domain shown in Figure 1, the expansion ratio ( ) is set equal to 2 in all of the test cases when the distance of baffle from the step depicted by D, is considered to be varied from
) is set equal to 2 in all of the test cases when the distance of baffle from the step depicted by D, is considered to be varied from  to
to . The computed domain in the x-direction downstream of the step is restricted by
. The computed domain in the x-direction downstream of the step is restricted by  and the distance between the inlet section and step depicted by a set equal to 10H to ensure fully developed condition for velocity and temperature distributions before the step.
and the distance between the inlet section and step depicted by a set equal to 10H to ensure fully developed condition for velocity and temperature distributions before the step.
First in order to show the flow pattern, the streamlines are plotted in Figure 5 for an inclined step with θ = 60˚ under the condition of ,
,  and Re = 500. The effects of step and baffle on the flow are clearly seen from the curvatures of streamlines and separated regions. Figure 5 shows that five different recirculation zones are encountered for Re = 500 in the flow domain. The primary recirculation region on the bottom wall occurs adjacent to the step upstream the baffle and the secondary one takes place on the bottom wall down stream the baffle, whereas three other recirculation zones occur adjacent to the baffle surface.
and Re = 500. The effects of step and baffle on the flow are clearly seen from the curvatures of streamlines and separated regions. Figure 5 shows that five different recirculation zones are encountered for Re = 500 in the flow domain. The primary recirculation region on the bottom wall occurs adjacent to the step upstream the baffle and the secondary one takes place on the bottom wall down stream the baffle, whereas three other recirculation zones occur adjacent to the baffle surface.
Since, the main task of the present study is to investigate the effect of baffle on the entropy generation in laminar forced convection flow, the following results shown in Figures 6 to 10 are due to air flows over inclined step with  for three different locations of baffle,
for three different locations of baffle,  and 3, three different baffle’s height,
and 3, three different baffle’s height,  and 0.5, when the baffle’s width is equal to H/2. In the computations of these figures, the Prandtl number is kept constant equal to 0.7 to guarantee constant fluid physical properties for moderate and small values of temperature difference
and 0.5, when the baffle’s width is equal to H/2. In the computations of these figures, the Prandtl number is kept constant equal to 0.7 to guarantee constant fluid physical properties for moderate and small values of temperature difference . The value of Reynolds number is equal to 500 except in Figures 9 and 10 in which the effect of Re on entropy generation and Bejan number is studied. Besides, the values of non-dimensional temperatures for bottom wall (including the step), top wall (including the baffle) and inlet fluid are set equal to 1, 0 and 0.7, respectively.
. The value of Reynolds number is equal to 500 except in Figures 9 and 10 in which the effect of Re on entropy generation and Bejan number is studied. Besides, the values of non-dimensional temperatures for bottom wall (including the step), top wall (including the baffle) and inlet fluid are set equal to 1, 0 and 0.7, respectively.
Variations of entropy generation number along the bottom wall at different locations of baffle and also at three different baffle’s heights are plotted in Figures 6(a) and (b), respectively. Also, the Ns variation in BFS flow without baffle is plotted in another coordinate system in Figure 6(a) because of different orders in the values of Ns. This figure shows that the baffle makes a different

Figure 5. Streamlines in flow over inclined step in a duct Re = 500, θ = 60˚, .
.
 (a)
(a) (b)
(b)
Figure 6. Variation of entropy generation numbers along the bottom wall Re = 500, θ = 60˚. (a) Effect of baffle location,
 ; (b) Effect of baffle height,
; (b) Effect of baffle height, .
.
trend for Ns distribution along the bottom wall in comparison to BFS flow without baffle. In the absence of baffle, the value of entropy generation number decreases along the step length and reaches to zero on the bottom wall at the step corner. After this point, Ns increases and the maximum value of Ns occurs inside the recirculation zone and then it drops sharply to a very low value at the reattachment point after which Ns increases and approaches to a constant value far from the step. This behavior can be explained by noting that after flow separation, the vortices increase dramatically inside the recirculation region that causes to take place maximum value of Ns in this zone. Besides, at the reattachment point no shear stresses are taking place and the entropy generation is totally due to conduction. But the presence of baffle causes a different trend for entropy generation number such that the baffle effect governs to the other factors in variation of entropy generation. According to Figure 6(a), the maximum entropy generation number occurs on the bottom wall just below the baffle with a value which is very greater than that of takes place for BFS flow excluding the baffle. For example in the case of , the maximum entropy generation number is about 80 times of the one for
, the maximum entropy generation number is about 80 times of the one for  (without baffle). This is related to the increased temperature and velocity gradients below the baffle where the flow is pushed toward the bottom wall. Also, it is seen from Figure 6(a) that the value of
(without baffle). This is related to the increased temperature and velocity gradients below the baffle where the flow is pushed toward the bottom wall. Also, it is seen from Figure 6(a) that the value of 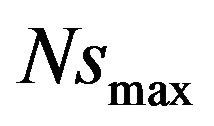 increases as the baffle moves toward the BFS (with the decrease of D). The effect of baffle height of the distribution of Ns along the bottom wall is indicated in Figure 6(b). This figure shows that the baffle height has an important effect on the variation of entropy generation umber such that the value of
increases as the baffle moves toward the BFS (with the decrease of D). The effect of baffle height of the distribution of Ns along the bottom wall is indicated in Figure 6(b). This figure shows that the baffle height has an important effect on the variation of entropy generation umber such that the value of  increases dramatically by a small increase in the height of baffle. It is also due to increasing in velocity and temperature gradients on the bottom wall by the baffle. Besides, it is seen from Figure 6(b) that the effect of recirculation region after the step on the variation of Ns becomes important for small value of the baffle height, such that for higher values for
increases dramatically by a small increase in the height of baffle. It is also due to increasing in velocity and temperature gradients on the bottom wall by the baffle. Besides, it is seen from Figure 6(b) that the effect of recirculation region after the step on the variation of Ns becomes important for small value of the baffle height, such that for higher values for , the variation of Ns is only affected by the baffle effect instead of flow separation and reattachment. It is worth mentioning that in Figure 6 and also in later similar figures for inclined step, the region
, the variation of Ns is only affected by the baffle effect instead of flow separation and reattachment. It is worth mentioning that in Figure 6 and also in later similar figures for inclined step, the region  is due to the step projected length after which there is the bottom wall.
is due to the step projected length after which there is the bottom wall.
Variations of Nusselt number on the bottom wall at different locations of the baffle and also at different baffle’s heights are plotted in Figures 7(a) and (b), respectively. For convection flow over BFS excluding the baffle ( ), it is seen from Figure 7(a) that Nu decreases along the step projected length and the minimum value of Nu occurs on the bottom wall adjacent to step corner and the maximum value at the reattachment point after witch Nu approaches to a constant value. In the presence of baffle, similar trend is seen for the variation of Nu on the bottom wall, but the maximum Nusselt number takes place just below the baffle with a value which is very grater than of the one for
), it is seen from Figure 7(a) that Nu decreases along the step projected length and the minimum value of Nu occurs on the bottom wall adjacent to step corner and the maximum value at the reattachment point after witch Nu approaches to a constant value. In the presence of baffle, similar trend is seen for the variation of Nu on the bottom wall, but the maximum Nusselt number takes place just below the baffle with a value which is very grater than of the one for . Besides, it is seen from Figures 7(a) and (b) that the maximum Nusselt number increases as the baffle moves toward the BFS and also by increasing in the baffle height.
. Besides, it is seen from Figures 7(a) and (b) that the maximum Nusselt number increases as the baffle moves toward the BFS and also by increasing in the baffle height.
Distributions of friction coefficient along the bottom wall at different baffle locations and also at different baffle’s height are illustrated in Figures 8(a) and (b), respectively. It is seen that  is negative inside the circulation zone due to the back flow and the minimum
is negative inside the circulation zone due to the back flow and the minimum
 (a)
(a) (b)
(b)
Figure 7. Variation of Nusselt number along the bottom wall. (a) Effect of baffle location, ; (b) Effect of baffle height,
; (b) Effect of baffle height, .
.
 (a)
(a) (b)
(b)
Figure 8. Variation of friction coefficient along the bottom wall Re = 500, θ = 60˚. (a) Effect of baffle location, hb/H = 0.5; (b) Effect of baffle height, D/H = 1.
value of friction coefficient takes place in this region after which the value of  becomes equal to zero at the point of reattachment. If one notices to the
becomes equal to zero at the point of reattachment. If one notices to the  curves in the vicinity of x = 0 in detail, it is seen that the value of friction coefficient is negative along the step projected length and then becomes zero at the step corner on the bottom wall. This is related to the fact that the surface of inclined step is exposed to the recirculation flow as shown in Figure 5. Increasing in the value of friction coefficient because of the baffle is very considerable, such that Figure 6(a) shows that for the case of
curves in the vicinity of x = 0 in detail, it is seen that the value of friction coefficient is negative along the step projected length and then becomes zero at the step corner on the bottom wall. This is related to the fact that the surface of inclined step is exposed to the recirculation flow as shown in Figure 5. Increasing in the value of friction coefficient because of the baffle is very considerable, such that Figure 6(a) shows that for the case of , that the maximum friction coefficient is about 15 times of the one in the absence of baffle. Comparison between the curves plotted in Figure 8 shows that the value of maximum friction coefficient which is takes place on the bottom wall below the baffle increases sharply as the baffle moves toward the BFS and also by increasing in the baffle height.
, that the maximum friction coefficient is about 15 times of the one in the absence of baffle. Comparison between the curves plotted in Figure 8 shows that the value of maximum friction coefficient which is takes place on the bottom wall below the baffle increases sharply as the baffle moves toward the BFS and also by increasing in the baffle height.
In the previous section, it was discussed that the amount of irreversibility in a fluid flow can be estimated by computing the total entropy generation in the flow domain. In order to show the effect of baffle on , Figure 9 shows the variation of total entropy generation in the flow domain against the Reynolds number for three different baffle locations and also for the convection flow over BFS without baffle. It is seen that the baffle has a considerable effect on the total entropy generation, such that the value of this parameter increases sharply by the baffle, especially as the baffle moves toward the BFS and at high values of Reynolds number. In a similar manner, the variations of average Bejan number with Re for three different baffle locations and also for the convection flow over BFS without baffle are plotted
, Figure 9 shows the variation of total entropy generation in the flow domain against the Reynolds number for three different baffle locations and also for the convection flow over BFS without baffle. It is seen that the baffle has a considerable effect on the total entropy generation, such that the value of this parameter increases sharply by the baffle, especially as the baffle moves toward the BFS and at high values of Reynolds number. In a similar manner, the variations of average Bejan number with Re for three different baffle locations and also for the convection flow over BFS without baffle are plotted

Figure 9. Total entropy generation v.s Reynolds number, θ = 60˚, hb/H = 0.5.
in Figure 10. As it was mentioned before, the Bejan number is the ratio of entropy generation due to conduction to the total entropy generation. Figure 10 shows that Be decreases as the baffle moves toward the BFS. Because under this condition, the value of velocity gradient on the bottom wall increases that causes an increase in the value . Besides it is seen that the average Bejan number decreases with increasing in Reynolds number. This is in consistent with the theoretical findings by Abu Nada [12].
. Besides it is seen that the average Bejan number decreases with increasing in Reynolds number. This is in consistent with the theoretical findings by Abu Nada [12].
7. Conclusion
The present research deals the second law analysis of

Figure 10. Variation of average Bejan number with Reynolds number, θ = 60˚, hb/H = 0.5.
convection laminar flow over inclined backward-facing steps in a duct with a baffle mounted onto the upper wall. The set of equations governs to the fluid flow, heattransfer and entropy generation is solved numerically by CFD techniques in the Cartesian coordinate system using blocked-off method. Results show that although the baffle enhances the convection coefficient on the bottom wall, but it causes a considerable increase in the value of entropy generation. Such that more irreversibilities take place in convection flow over BFS as the baffle moves toward the step, especially for high value of the baffle height and at high Reynolds number.
REFERENCES
- B. F. Armaly, F. Durst, J. C. F. Pereira and B. Schonung, “Experimental and Theoretical Investigation of Backward-Facing Step Flow,” Journal of Fluid Mechanics, Vol. 127, 1983, pp. 473-496. Hdoi:10.1017/S0022112083002839
- G. C. Vradis, V. Outgen and J. Sanchez, “Heat Transfer over a Backward-Facing Step: Solutions to a Benchmark,” Benchmark Problems for Heat Transfer Codes, ASME HTD, Anaheim, 1992, pp. 27-34.
- D. W. Pepper, K. L. Burton and F. P. Bruenckner, “Numerical Simulation of Laminar Flow with Heat Transfer over a Backward-Facing Step,” Benchmark Problems for Heat Transfer Code, ASME HTD, Anaheim, 1992, pp. 66-80.
- G. Vradis and L. Van Nostrand, “Laminar Coupled Flow Downstream an Asymmetric Sudden Expansion,” Journal of Thermophysics Heat transfer, Vol. 6, No. 2, 1992, pp. 288-295. Hdoi:10.2514/3.357
- L. Kaiktsis, G. E. Karniadakis and S. A. Orszag, “Onset of Three-Dimensionality Equilibria, and Early Transition in Flow over a Backward-Facing Step,” Journal of Fluid Mechanics, Vol. 231, 1991, pp. 501-528. Hdoi:10.1017/S0022112091003488
- N. Tylli, L. Kaiktsis and B. Ineichen, “Side Wall Effects in Flow over Backward-Facing Step: Experiments and Numerical Solutions,” Physics of Fluids, Vol. 14, No. 11, 2002, pp. 3835-3845. Hdoi:10.1063/1.1506163
- D. Brakely, M .Gabriela, M. Gomes and R. D. Henderson, “Three-Dimensional Instability in Flow over a Backward-Facing Step,” Journal of Fluid Mechanics, Vol. 473, 2002, pp. 167-190.
- H. I. A. Mulaweh, “A Review of Research on Laminar Mixed Convection Flow over Backwardand Forward-Facing Steps,” International Journal of Thermal Sciences, Vol. 42, No. 9, 2003, pp. 897-909. Hdoi:10.1016/S1290-0729(03)00062-0
- J. H. Nie, Y. T. Chen and H. T. Hsieh, “Effects of a Baffle on Separated Convection Flow Adjacent to Backward-Facing Step,” International Journal of Thermal Sciences, Vol. 48, No. 3, 2009, pp. 618-625. Hdoi:10.1016/j.ijthermalsci.2008.05.015
- E. Abu Nada, “Numerical Prediction of Entropy Generation in Separated Flows,” Entropy, Vol. 7, No. 4, 2005, pp. 234-252. Hdoi:10.3390/e7040234
- E. Abu Nada, “Entropy Generation Due to Heat and Fluid Flow in Backward-Facing Step Flow with Various Expansion Ratios,” International Journal of Exergy, Vol. 3, No. 4, 2006, pp. 419-435. Hdoi:10.1504/IJEX.2006.010234
- E. Abu Nada, “Investigation of Entropy Generation over a Backward-Facing Step under Bleeding Conditions,” Energy Conversion and Management, Vol. 49, No. 11, 2009, pp. 3237-3242. Hdoi:10.1016/j.enconman.2007.10.031
- S. V. Patankar, “Numerical Heat and Mass Transfer and Fluid Flow,” Hemisphere Publishing Corporation, Washington DC, 1980.
- A. Bejan, “Entropy Generation through Heat and Fluid Flow,” Wiley, New York, 1982.
- S. V. Patankar and B. D. Spalding, “A Calculation Procedure for Heat, Mass and Momentum Transfer in ThreeDimensional Parabolic Flow,” International Journal of Heat Mass Transfer, Vol. 15, No. 10, 1972, pp. 1787- 1806. doi:10.1016/0017-9310(72)90054-3
Nomenclature
a distance between inlet section and step (m)
 width of baffle (m)
width of baffle (m)
Be Bejan number
(x, y) coordinates (m)
Br Brinkman number
(X,Y) dimensionless coordinates
 coefficient of friction
coefficient of friction
Greek Symbols
ER expansion ratio (H/h)
![]() thermal diffusivity (m2/s)
thermal diffusivity (m2/s)
H channel height (m)
 step inclined angle h step height (m)
step inclined angle h step height (m)
 dynamic viscosity (N∙s∙m−2)
dynamic viscosity (N∙s∙m−2)
 baffle height (m)
baffle height (m)
 density (kg∙m3)
density (kg∙m3)
k thermal conductivity (W∙m−1∙K−1)
![]() dimensionless temperature parameter L length of the channel (m)
dimensionless temperature parameter L length of the channel (m)
 non-dimensional temperature
non-dimensional temperature
 characteristic length (m)
characteristic length (m)
![]() kinematic viscosity (m2/s)
kinematic viscosity (m2/s)
Ns entropy generation number
 viscous dissipation number Nu Nusselt number
viscous dissipation number Nu Nusselt number
Subscripts
P dimensionless pressure
b baffle p pressure (Pa)
cond conduction
Pr Prandtl number
visc viscous Re Reynolds number
w wall
![]() volume rate of entropy generation (W∙m−3∙K−1)
volume rate of entropy generation (W∙m−3∙K−1)
m mean bulk value
 temperature (K)
temperature (K)
 inlet fluid temperature (K)
inlet fluid temperature (K)
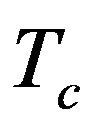 temperature of cold wall (K)
temperature of cold wall (K)
 temperature of hot wall (K)
temperature of hot wall (K)
(u, v) xand y-velocity components  (U, V) dimensionless xand y-velocity components.
(U, V) dimensionless xand y-velocity components.
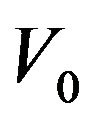 inlet fluid velocity
inlet fluid velocity 

