Received 24 October 2014; revised 8 December 2014; accepted 22 December 2014

ABSTRACT

The carrier dynamics in organic photovoltaic (OPV) cells were investigated by impedance spectroscopy. We introduced a novel impedance spectrum representation called dynamic modulus plot (DMP), which allowed us to observe the layer-to-layer carrier injection behavior graphically. In this work, the impedance responses were characterized in the N,N’-diphenyl-N,N’-di-m-tolyl- 4,4’-diaminobiphenyl (TPD)/C₆₀ p-n heterostructured OPV cells against applied voltages. The dependence of impedance responses on the layer thickness revealed a constant internal electric field that disturbed the carrier transport within the OPV cells. We applied this technique to new donor materials, in which thiophene units were inserted to the center of TPD. By increasing the number of thiophene units in TPD the fill-factor (FF) improved from 33% to 59%, which increased the power conversion efficiency (PCE). Based on the DMP analysis, we assigned the improvement in device performance to the reduction of the internal electric field.

Keywords:

Organic Photovoltaic Cells, Impedance Spectroscopy, Modulus Analysis

1. Introduction

In 1986, Tang fabricated a bilayer heterojunction solar cell with an efficiency approaching 1%, which was a milestone in the development of organic photovoltaic (OPV) cells [1] . Since the innovation of Tang’s layered thin film structure, which separates specific functionalities into discrete layers, organic electronic devices have experienced dramatic improvement. In recent years, the power conversion efficiency and the durability of the OPV cells have rapidly improved thanks to the efforts of many researchers [2] -[5] . However, the carrier dynamics in the OPV cells are still not fully understood because of the complexity of the interactions between each organic layer. By using intensity-modulated photocurrent spectroscopy (IMPS), Forrest et al. reported that the donor- acceptor interface interactions in p-n heterostructured OPV cells was governed by the separation of polaron pairs and the carrier recombination rate [6] . Iwamoto et al. have analyzed the carrier accumulation behavior using a combination of electric-field-induced second harmonic generation and impedance spectroscopy (IS), which indicated that the Maxwell Wagner effect was present at the interface between pentacene and C₆₀ [7] . Furthermore, Ishii et al. revealed that a giant surface potential (GSP) was present within the organic electron transporting layer deposited on anorganic hole transporting layer by means of photoelectron spectroscopy and displacement current measurements [8] [9] . To improve device performance, carrier transport analysis of organic heterostructured devices is important. Carrier behavior in organic devices, such as charge separation and recombination, is governed by the interaction of donor-acceptor interfaces because organic materials have very few carriers. Therefore, understanding carrier behavior at the donor-acceptor interface is necessary to further improve organic devices. Standard current-voltage (J-V) measurements only give general information about the carrier transport. To obtain deeper physical insight into the carrier transport, information about the layer-to-layer carrier dynamics in each layer is needed. Impedance spectroscopy is a well-known and fundamental technique to investigate the electric response of structured devices composed of multi-circuit elements [10] .

In this study, the basic carrier dynamics in p-n heterostructured OPV cells were investigated using impedance spectroscopy. We introduced a novel representation of the impedance spectrum dynamic modulus plot (DMP), which allowed us to graphically observe the layer-to-layer carrier injection and carrier accumulation behavior. The diode characteristics of the OPV cells were discussed based on the analysis of the charge carrier behavior by means of DMP analysis in the dark. We revealed the existence of an internal electric field at the donor- acceptor interface, which governed the OPV device performance under the illumination.

2. Experimental Methods

2.1. Device Preparation

The compounds TPD, C₆₀ and bathocuproine (BCP) were purchased from Sigma-Aldrich Co. Ltd. Bis-diphe- nylaminophenyloligothiophene (BDA-Tn [n = 1 - 3]) derivatives were synthesized using the Suzuki-Miyaura coupling reaction in our laboratory. These materials were purified by vacuum sublimation at 10⁻³ Pa. OPV cells with the layered structure ITO/p-type/C₆₀/BCP/Al were fabricated by vacuum deposition. ITO substrates, purchased from Asahi Glass Co., Ltd, with a sheet resistance of 25 Ω/sq were ultrasonicated first in 2-propanol and then in ultra-pure water. They were later exposed to an ultraviolet-ozone surface treatment and transferred to a vacuum chamber. The organic materials were evaporated onto the substrates under a vacuum pressure of less than 10⁻⁴ Pa, with deposition rates between 1 and 5 Å/s. The active area of the diodes was 5.8 mm². The devices were measured in ambient atmosphere without encapsulation.

2.2. Device Characterization

The highest occupied molecular orbital (HOMO) energy levels of the organic materials were determined by photoelectron yield spectroscopy in air using an AC-3 spectrometer (Riken Keiki Co. Ltd., Japan). The film absorption spectra were recorded by a UV-3600 UV-Vis-NIR spectrophotometer (Shimadzu Co. Ltd., Japan). The optical band gaps were estimated from the absorption edge of the thin films. The lowest unoccupied molecular orbital (LUMO) energy levels were estimated by the subtraction of the optical band gap from the HOMO levels.

The J-V characteristics of the devices were measured at room temperature with a source measurement unit (Keithley Instruments Inc., 2400) in the dark and under illumination of 100-mW/cm² white light provided by a 1.5 AM solar simulator.

The impedance measurements were performed with an impedance analyzer (Agilent Technologies Inc., 4294A) in the frequency range from 100 Hz to 1 MHz in the dark. The AC modulation amplitude was kept as low as 50 mV, where the response to the AC amplitude was linear. The complex impedance data were transferred to a PC and processed mathematically to appropriate representations.

2.3. Analysis of Dynamic Modulus Plot (DMP)

In general, electronic devices are represented by a combination of capacitance and resistance components in response to an external field. Carrier density and electron levels are evaluated based on C-V and f-C measurements in semiconductor engineering. In the electrochemical field, Cole-Cole plots, which are a representation of the impedance spectrum, have been used frequently [11] . The equivalent circuits of p-n heterostructured OPV, which separates specific functionalities to discrete layers, are complex components of each element. It is necessary to separate and analyze the individual responses of the components. Therefore, Cole-Cole plots are used to perform the separation and analysis using the difference in the frequency response of each element. By plotting the complex modulus data on a complex plain, we obtain an impedance Cole-Cole plot. In conventional p-n junction theory, negative bias voltage places the carrier away from the junction. This depleted region works as a capacitor, which is connected to the conductive region. Therefore, the equivalent circuit is a series connection of a resistor and a capacitor. However, organic materials have very few free carriers so that they are not semiconductor but dielectrics. Therefore, organic layers are well represented by equivalent circuits of capacitance resistance (CR) parallel circuits. The impedance (Z) of an organic layer is described by Equation 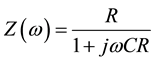(1).

(1)

becomes a semicircle in the Cole-Cole plot, which is the Nyquist plot of imaginary Z vs real Z. The radius of this impedance Cole-Cole plot corresponds to the resistance of the layer. The impedance of the layered devices is described as the sum of Equation (1). The impedance representation can be translated to the capacitance representation, which is called the modulus (M), defined by:

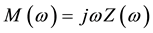(2)

When an arc appears in the impedance Cole-Cole plot, a corresponding arc appears in the modulus Cole-Cole plot. Its diameter is the reciprocal value of capacitance (C) (Figure 1). Because the dielectric constants are mostly 3.0 in many organic materials, the diameter of the arc rescaled by the surface area (S) in the modulus representation represents the effective thickness of the film. The semicircle means that carriers accumulate in the dielectric regions which become conductive. The stacked layers are represented by a series connection of these CR parallel equivalent circuits. The value of the x-coordinate component in the modulus Cole-Cole plot becomes the effective thickness by rewriting the real part of the modulus as d = εε₀S ReM (ω). It is easy to identify which arc corresponds to which layer by observing the correspondence between the effective film thickness, estimated from the capacity, and the planned film thickness.

Here we propose a new graphical representation for the voltage-current response function, the dynamic modulus plot (DMP). The DMP is a compilation of the modulus plots obtained by frequency sweep, which are measured under various bias voltage conditions. The frequency sweep of the current response to the small AC modulation voltage is recorded for various DC bias voltages. The data obtained from the frequency sweep are converted to complex modulus data. By plotting the complex modulus data on a complex plain, we obtain a modulus Cole-Cole plot. The modulus Cole-Cole plots for various bias voltages are re-plotted so their imaginary parts are offset by the bias voltage, and the imaginary parts are rescaled by arbitrary values. Usually, the semicircles of organic electronic devices in the Cole-Cole plots are expressed by precise circles such that the lack of the scale of the imaginary part does not cause any confusion. We call this compilation of the modulus plots the DMP. Here, we note that the envelope at the lowest frequency points is the Mott-Schottky plot.

3. Results and Discussion

3.1. Equivalent Circuit Model and Modulus Plot of p-n Heterostructured OPV Cell

Figure 2(a) shows the J-V characteristics of the p-n heterostructured OPV cell. The OPV cell had an open-cir- cuit voltage (V_oc) of 0.86 V, a short-circuit current density (J_sc) of 2.37 mA∙cm⁻², a fill factor (FF) of 33%, and

a power conversion efficiency (η) of 0.67% under AM 1.5, 100 mW・cm⁻² simulated solar light. Impedance and modulus Cole-Cole plots of the OPV cell are shown in Figure 2(b) and Figure 2(c). The advantage of using modulus over impedance is that it is a unified view of the Cole-Cole plot, which makes clear the equivalent circuits, and the Mott-Schottky plot, which indicates the accumulation behavior of the carriers. As shown in Figure 2(c), some semicircles were observed in the modulus Cole-Cole plot. In this case, the change of the semicircle radius represents how deep the carrier accumulates in the layer. The impedance Cole-Cole plot provided the resistance information about the OPV devices for several layers. While only one arc was observed in the impedance Cole-Cole plot, several arcs corresponding to the different layers were clearly identified in the modulus Cole-Cole plot (Figure 2(c)).

In Figure 3, the modulus data of the OPV cell in the dark condition under 0.7 V bias were fitted by the simple equivalent circuit models. The equivalent circuit of p-n heterostructured OPV cells was explained by the model which is connected with CR parallel circuits of three layers corresponding to an individual layer.

3.2. DMP of p-n Heterostructured OPV Cells

Figure 4 shows examples of the DMP of the OPV p-n cells with different layer thicknesses. The structure of the devices was ITO/mTPD (X)/C₆₀(60 − X)/BCP/Al, in which layer thickness X was changed from 20, 30 and 40 nm respectively. As shown in this figure, the inverse of capacitance at high frequency (right-hand edge) is mostly constant, which corresponds to the invariance of the device against applied voltage over the range of layer thicknesses measured. From this figure, it is easy to determine at which voltage and to which layer the carriers accumulate.

From DMP, changes to the circuits of OPV devices can be seen. At sufficiently low bias voltage, there is only a small semicircle and a vertical line at the high frequency side. The vertical line means the device is an insulator and the electric response is purely dielectric. As the bias voltage increases, several semicircles appear and merge. The small semicircles correspond to p-type and n-type organic layers in which carriers were injected and were conductive. The equivalent circuits of the devices changed to a parallel connection of resistance and capacitance from pure capacitance. Finally, only one semicircle remained at sufficiently high voltage. There was a small semicircle at the high frequency side below a bias voltage of −1.0 V in all three devices. Compared with the designed thickness, the semicircle was assigned to a BCP layer. It is surprising that electrons accumulate in the BCP layer at such low bias voltages. The carrier accumulation in a BCP layer adjacent to a C₆₀ layer was confirmed by photoelectron yield spectroscopy and displacement current measurements [9] . The semicircle that appeared at the high frequency side was assigned to the C₆₀ layer and the semicircle that appeared at the lower frequency side was assigned to the mTPD layer. The assignment is obvious because the radius at the lower frequency side is proportional to the designed mTPD thickness. In Figure 4, as the mTPD layer thickness increases, the radius of the semicircle at the lower frequency increases.

The radius of the semicircle at higher frequency becomes smaller by decreasing the layer thickness of the C₆₀ layer. The separation of these two semicircles comes from the Maxwell-Wagner effect, i.e. the difference in the relaxation time in each layer [7] . After injection, the two semicircles merge to one semicircle. Because the voltage is applied mainly to the highest resistance layer, the conductivity increase is greater than that of lower resistance layer. Because the conductivity and the relaxation time balance at high voltage, all the semicircles coalescence into one. The change of the electric properties of each layer in multilayered devices can be understood graphically from the DMP. In Figure 4(b), the semicircle becomes larger as the bias voltage increases from −1.0 to 0.7 V, which means the thickness of the conductive C₆₀ layer becomes larger through carrier accumulation. As the voltage increases, a small semicircle evolves and increases its radius. After its radius saturates, a new semicircle evolves from 0.7 V (the voltage is mostly independent of the layer thickness). This is the start of carrier injection into the mTPD layer. These two semicircles merged to one semicircle at high voltage. This value corresponds to the threshold voltage of current density increase in J-V characteristics of this device. The accumulation of electrons in C₆₀ starts at −0.3 V (x = 20 nm), −0.6 V (x = 30 nm), and −0.9 V (x = 40 nm), as indicated by lines in Figure 4. The threshold voltage (V_th) at which accumulation in the C₆₀ layer starts is proportional to the layer thickness. It means that a constant internal electric field exists in the OPV cells. When we differentiate the voltage shift against the layer thickness, the internal electric field was estimated to be 30 mV/nm. The corresponding surface charge density is 0.80 mC/m² using a dielectric constant of 3.0. This carrier accumulation behavior at the organic hetero-interfaces has been observed in multilayer organic light-emitting diodes (OLEDs) [12] [13] . Interface charge was first detected by Brütting et al. at the a-NPD/Alq3 interface in a bilayer OLED. Furthermore, Ishii et al. reported clear GSP behavior with a slope of 48 mV/nm, which corresponds to an interface charge density of 1.36 mC/m² [14] . In our study, the carrier accumulation at the TPD/C₆₀ interface was observed by the DMP analysis, which is similar to previous reports. With DMP analysis we can observe complex charge accumulation behavior at a glance without any simulation. Because this internal electric field can

suppress the charge dispersion along the donor-acceptor interface in the dark condition of the OPV cells, the reduction of the internal electric field is quite important to improve of the diode characteristics of OPV cells.

3.3. DMP with Varied p-Type Materials

The charge accumulation properties of bilayer devices composed of new p-type materials, bis-diphenylamino- phenyloligothiophenes (BDA-Tn), were examined by impedance spectroscopy. Oligothiophenes are one of the largest families of organic semiconductors, and have been widely used in OPVs because of their high charge- carrier mobility and facile synthesis for tuning energy levels [15] . We have investigated the dependence of PCE on the conjugation length by the incident photon-to-electron conversion efficiency (IPCE) action spectrum.

The new donor materials BDA-Tn were expected to show high PCEs, because their conjugation lengths are longer than mTPD, i.e. they can absorb more of the AM 1.5 spectrum. To investigate the effect of conjugation length, we inserted different numbers of thiophene units into the TPD skeleton.

Figure 5 shows the typical current density-voltage characteristics of the OPV cells based on the BDA-Tn derivatives, BDA-T0 (○), BDA-T1 (●), BDA-T2 (▲), BDA-T3 (◆) under illumination of AM 1.5, 100 mW∙cm⁻². The structures of the devices were ITO/BDA-Tn/C₆₀/BCP/Al. The photovoltaic parameters are listed in Table 1.

As the number of thiophene units increases, V_oc of the BDA-Tn/C₆₀ cells was reduced and the J_sc and FF improved significantly. The highest power conversion efficiency in this series of materials was achieved with BDA-T3, which reached 1.33%.

The reduction of the V_oc was attributed to the relatively low ionization potential of the BDA-Tn materials. The improvement of the J_sc was caused by the stronger absorption of the solar light. BDA-T3, which has three thiophene units, exhibited an absorption peak around 440 nm which is a bathochromic shift of ~30 nm compared with mTPD (λ_max = 410 nm).

The layer resistivity is closely related to the carrier mobility of the material and the FF in OPV cells. We measured the mobilities of the BDA-Tn derivatives by TOF methods. The measured mobilities of the BDA-Tn derivatives were 1.0 × 10⁻³ cm²∙V⁻¹∙s⁻¹ (BDA-T0 or mTDP), 4.8 × 10⁻⁴ cm²∙V⁻¹∙s⁻¹ (BDA-T1), 1.6 × 10⁻⁴ cm²∙V⁻¹∙s⁻¹ (BDA-T2), and 4.9 × 10⁻⁵ cm²∙V⁻¹∙s⁻¹ (BDA-T3). It is puzzling that the mobilities decrease as the number of thiophene units increases, whereas the FF improves with the number of thiophene units. Generally, TOF measurements are carried out with a high electric field, but OPV cells are driven under very low electric fields (so called built-in potentials). These electric field differences may make it difficult to interpret the TOF results.

To understand why the FF improves, we have carried out an impedance analysis of the OPV cells composed of BDA-Tn derivatives. In Figure 6, the accumulation of electrons in C₆₀ starts at −0.6 V (BDA-T0), −0.4 V (BDA-T1), −0.3 V (BDA-T2), and −0.1 V (BDA-T2), as indicated by lines. As the number of thiophene units increases, the V_th of carrier accumulation in the C₆₀ layer becomes higher (Figure 6). The change of these threshold voltages V_th means the change of the internal electric field in each OPV cell. The more thiophene units there are, the smaller the internal electric field in the OPV cell becomes. The internal electric field works to disturb the carrier transport to the each electrode. We speculate that reduction of the internal electric field is the reason for the improvement of the FF in OPV cells.

4. Conclusions

In this work, we have investigated the impedance response of TPD/C₆₀ p-n heterostructured OPV cells against applied voltages. The equivalent circuit of p-n heterostructured OPV cells can be explained by three connected CR parallel circuits, each of which corresponds to a layer of the device.

As a result of the modulus analysis, the threshold voltage for charge injection and accumulation within the C₆₀ layer varied in proportion to the film thickness. We have found that a constant internal electric field exists which disturbs the carrier transport to the electrodes in OPV cells because of interactions at the donor-acceptor interface. It is thought that this internal electric field is the reason for the reduction of the FF of OPV cells.

Next, new donor materials BDA-Tn were investigated. By increasing the number of thiophene units in BDA- Tn the power conversion efficiency and FF increased significantly, from 33% to 59%. Based on the DMP analysis, we found that the internal electric field decreased by introducing more thiophene units and concluded that the reduction of the internal electric field was the reason for the improved device performance. Further investigation of this phenomenon to reduce the internal electric field will potentially lead to higher-efficiency organic heterostructured solar cells.

References

NOTES

^*Corresponding author.