Advances in Materials Physics and Chemistry
Vol.4 No.6(2014), Article
ID:46916,11
pages
DOI:10.4236/ampc.2014.46013
On DFT Molecular Simulation for Non-Adaptive Kernel Approximation
Maharavo Randrianarivony
Virtual Material Design, Fraunhofer Institute for Algorithms and Scientific Computing SCAI, Schloss Birlinghoven, Sankt Augustin, Germany
Email: randrian@ins.uni-bonn.de
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 April 2014; revised 4 June 2014; accepted 11 June 2014
ABSTRACT
Using accurate quantum energy computations in nanotechnologic applications is usually very computationally intensive. That makes it difficult to apply in subsequent quantum simulation. In this paper, we present some preliminary results pertaining to stochastic methods for alleviating the numerical expense of quantum estimations. The initial information about the quantum energy originates from the Density Functional Theory. The determination of the parameters is performed by using methods stemming from machine learning. We survey the covariance method using marginal likelihood for the statistical simulation. More emphasis is put at the position of equilibrium where the total atomic energy attains its minimum. The originally intensive data can be reproduced efficiently without losing accuracy. A significant acceleration gain is perceived by using the proposed method.
Keywords:DFT, Energy, Stochastic, Covariance, Hyperparameter

1. Introduction
Nanotechnology tends to be the technology of focus in this century [1] . Many of the macroscopically visible continuum applications seem to have attained nearly optimal state in computer implementation as well as in theoretical analysis. Not only the analytical and numerical treatments of nanotechnology are interesting but it has real-world applications in various disciplines including aircraft, automobile, electronic and medical engineering. This work is partially a continuation of our former studies in [2] -[4] but we consider here electronic structures instead of solute-solvent interactions. In this paper, we would like to concentrate on the efficient treatment of quantum information. We present a method which is efficient for noisy data that contain measurement imperfection because quantum data measurements are not completely ab-initio. Among other methods, DFT (Density Functional Theory) contains some parameters which are obtained from fitting procedures. Our motivation is to generate a system which is both accurate and fairly inexpensive to evaluate. Our method applies to all sorts of quantum information but we focus on the atomic energy in this paper. The availability of efficient and accurate evaluations can be used for subsequent applications. The region where the system admits its equilibrium is examined more carefully than the remaining region during the approximation. That is, a geometry optimization must be performed initially in order to determine the position where the energy attains its minimum. The most general setup enables an estimation of an unknown function in arbitrary dimension such that noisy sample functions together with their higher derivatives are provided. In this document, we treat the simplified version where only the sample values are provided. Depending on the desired accuracy and the size of the atomic system, the determination of the energy can last several minutes till several hours by using direct DFT computations. The molecular configurations consist of germanium, silicon or composites of them using several space group symmetries. The function to be reconstructed is the energy surface of a configuration when some tensor transformations are applied to DFT. The possible transformations include isotropic stretching, anisotropic stretchings and Voigt tensor. Our numerical experiments reveal that the proposed statistical pre-fitting process seems to be a reasonable approach to obtain a good accuracy in an affordable computing time. The preparation overhead lasts very long but it needs only to be performed once for all and its output can be stored. The acceleration factor between the direct DFT and the kernel based approximation is approximately of order 105. Due to this significant acceleration gain, the preparation process shows to be worth calculating.
2. Theoretical Methodology
2.1. Ground State Energy
For a configuration of nuclei 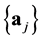 of number
of number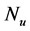 , the main problem in electronic structure computation involves the general Hamiltonian operator. We denote the coordinates of the i-th electron by
, the main problem in electronic structure computation involves the general Hamiltonian operator. We denote the coordinates of the i-th electron by 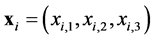
and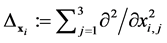 . For the Born-Oppenheimer or adiabatic approximation, one assumes that the mass and the volume of the atoms are very large in comparison to those of the electrons. Thus, the atoms move comparatively slower than the electrons. As a consequence, one treats the time-independent Hamiltonian operator with respect to a set of nuclei
. For the Born-Oppenheimer or adiabatic approximation, one assumes that the mass and the volume of the atoms are very large in comparison to those of the electrons. Thus, the atoms move comparatively slower than the electrons. As a consequence, one treats the time-independent Hamiltonian operator with respect to a set of nuclei 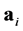 which are supposed to be stationary. That is, the electronic structure is governed by the expression
which are supposed to be stationary. That is, the electronic structure is governed by the expression
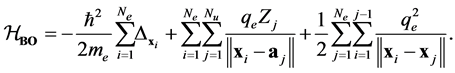 (1)
(1)
The above three terms are related to the kinetic energy, the atom-electron interaction and the inter-electron interaction while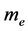 ,
, 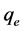 ,
, 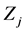 ,
, 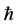 are quantum parameters. The domain of computation is
are quantum parameters. The domain of computation is 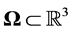 which is supposed to be sufficiently larger than the nuclei cloud
which is supposed to be sufficiently larger than the nuclei cloud 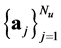 such that the above operator has neglecting influence beyond
such that the above operator has neglecting influence beyond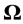 . By considering the electron spins which take values
. By considering the electron spins which take values 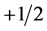 or
or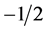 , we are searching for the electronic wave function
, we are searching for the electronic wave function
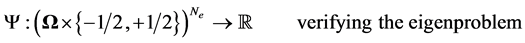
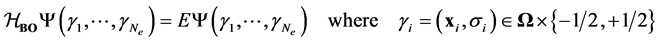 (2)
(2)
such that 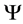 is antisymmetric
is antisymmetric 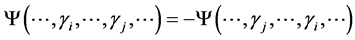 for all distinct
for all distinct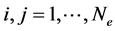 . The ground state energy corresponds to the smallest eigenvalue
. The ground state energy corresponds to the smallest eigenvalue 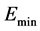 of (2). The anti-symmetrization operator
of (2). The anti-symmetrization operator 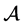 applied to any
applied to any 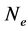 -variate function
-variate function 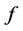 is defined by
is defined by
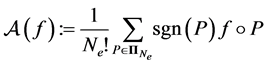 (3)
(3)
in which 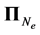 is the set of permutations over
is the set of permutations over 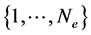 and
and 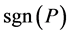 designates the signature of a permutation
designates the signature of a permutation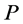 . If
. If 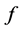 is a tensor product function as
is a tensor product function as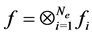 , then the anti-symmetrizer coincides with the Slater determinant or wedge product
, then the anti-symmetrizer coincides with the Slater determinant or wedge product
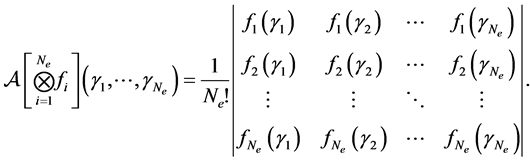 (4)
(4)
The anti-symmetrization operator 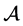 has the properties that it commutes with the Hamiltonian operator and that for an
has the properties that it commutes with the Hamiltonian operator and that for an 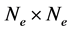 matrix
matrix 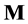 one has
one has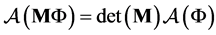 . The Hartree-Fock approach is the variational formulation on the Hamiltonian operator (1) where the trial functions are antisymmetric functions. The main difficulty is that the problem is of
. The Hartree-Fock approach is the variational formulation on the Hamiltonian operator (1) where the trial functions are antisymmetric functions. The main difficulty is that the problem is of 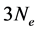 -dimension without taking the electronic spins into account. In addition, on account of the antisymmetric property, a direct use of the Slater determinant often produces computations having orders of
-dimension without taking the electronic spins into account. In addition, on account of the antisymmetric property, a direct use of the Slater determinant often produces computations having orders of 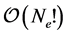 which are very expensive. Counting the electronic spins leads usually to a factor of
which are very expensive. Counting the electronic spins leads usually to a factor of 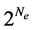 which makes the computation even more intractable. Some simplifications of the stationary Hamilton operators have already been proposed. For the DFT, one solves a set of equations for each electron. The similarity of the solutions is then derived from the theory of Kohn-Sham [5] which consists in replacing the complicated initial problem into several ones. For each
which makes the computation even more intractable. Some simplifications of the stationary Hamilton operators have already been proposed. For the DFT, one solves a set of equations for each electron. The similarity of the solutions is then derived from the theory of Kohn-Sham [5] which consists in replacing the complicated initial problem into several ones. For each 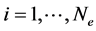
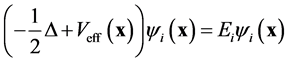 (5)
(5)
where 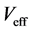 is the effective potential energy which depends implicitly on the total electron density
is the effective potential energy which depends implicitly on the total electron density
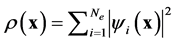 such that
such that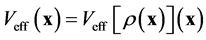 . The problem (2) is then reduced from dimensions
. The problem (2) is then reduced from dimensions
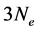 to
to 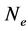 sets of
sets of 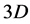 smaller problems (5). The influence of one electron with respect to the other electrons is measured by the total electron density. These approaches enable the treatment of Hamiltonian problem even for an electronic structure having a large number of particles on a single desktop. The effective potential is constituted of the Hartree potential
smaller problems (5). The influence of one electron with respect to the other electrons is measured by the total electron density. These approaches enable the treatment of Hamiltonian problem even for an electronic structure having a large number of particles on a single desktop. The effective potential is constituted of the Hartree potential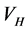 , the exchange correlation potential
, the exchange correlation potential 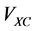 and the external electrostatic field such as
and the external electrostatic field such as
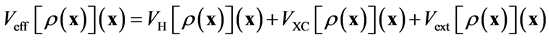 (6)
(6)
in which the Hartree potential is the inverse of the Poisson operator such as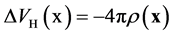 . For its evaluation, either a Poisson problem is solved or one convolves with the Green fundamental solution such as
. For its evaluation, either a Poisson problem is solved or one convolves with the Green fundamental solution such as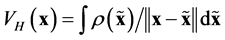 . The exchange-correlation potential is some correction term [6] which is usually done by LDA (Local Density Approximation) or GGA (Generalized Gradient Approximation). Analytic expressions of the correlation energy are only known in a few special cases which mainly consist of the high and low density limits. The exchange-correlation potential is related to the exchange-correlation energy by
. The exchange-correlation potential is some correction term [6] which is usually done by LDA (Local Density Approximation) or GGA (Generalized Gradient Approximation). Analytic expressions of the correlation energy are only known in a few special cases which mainly consist of the high and low density limits. The exchange-correlation potential is related to the exchange-correlation energy by 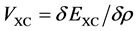 where one expresses
where one expresses 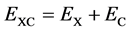 as the exchange and the correlation parts. In term of the exchange-correlation energy density
as the exchange and the correlation parts. In term of the exchange-correlation energy density 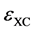 one has
one has
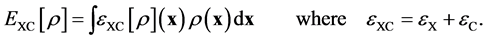 (7)
(7)
For the local density approximation (LDA), the exchange energy density is expressed as
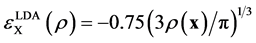 so that
so that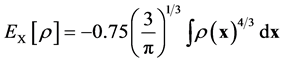 . Analytic values of the correlation energy density are only known for some extreme cases. The external electrostatic field potential
. Analytic values of the correlation energy density are only known for some extreme cases. The external electrostatic field potential 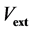 is provided by the kernel
is provided by the kernel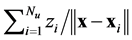 . Once the solution
. Once the solution 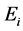 to (5) for all
to (5) for all 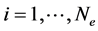 becomes known, the Khon-Sham approach uses the approximation to
becomes known, the Khon-Sham approach uses the approximation to 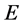 of (2) by
of (2) by
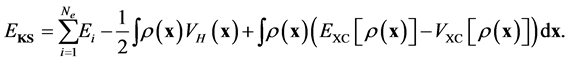 (8)
(8)
The main improvement from LDA to GGA is that the exchange-correlation energy does not depend only on the total electron density but also on its gradient such as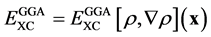 . Because of the imperfections resulting from the estimation of parameters from experimental measurements, the DFT approach is not ab-initio as in the initial equations. But the statistical fitting approach proposed in this paper can deal with noisy data. The eigenvalue problem in (5) is nonlinear because its variational operator
. Because of the imperfections resulting from the estimation of parameters from experimental measurements, the DFT approach is not ab-initio as in the initial equations. But the statistical fitting approach proposed in this paper can deal with noisy data. The eigenvalue problem in (5) is nonlinear because its variational operator
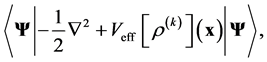 (9)
(9)
depends on  which in turn depends on
which in turn depends on . It is solved by using a sequence of the linear eigenvalue problems SCF (Self Consistent Field). After assembling the operator (9), the linear eigenvalue problem is solved for the smallest eigenvalue
. It is solved by using a sequence of the linear eigenvalue problems SCF (Self Consistent Field). After assembling the operator (9), the linear eigenvalue problem is solved for the smallest eigenvalue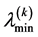 . Then, the new iterate
. Then, the new iterate 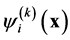 is determined as the eigenfunction corresponding to
is determined as the eigenfunction corresponding to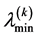 . In practice, one represents
. In practice, one represents 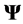 as a set of basis [7] which are usually plane waves, Finite Element Method, or wavelets.
as a set of basis [7] which are usually plane waves, Finite Element Method, or wavelets.
2.2. Kernel-Based Approximation
In this section, we will survey the main points about kernel-based approximation which are relevant in the quantum approximation. The most general setup of that approximation in any dimension 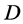 consists in accepting some inputs which are
consists in accepting some inputs which are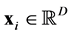 ,
, 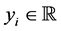 ,
, 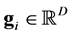 and
and 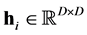 such that
such that
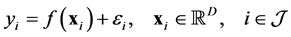 (10)
(10)
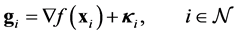 (11)
(11)
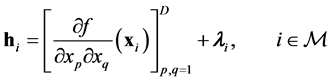 (12)
(12)
in which 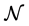 and
and 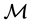 are some subsets of
are some subsets of 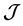 while
while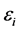 ,
, 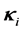 ,
, 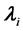 are measurement imperfections. In general, using the gradients is computationally very expensive so that the set
are measurement imperfections. In general, using the gradients is computationally very expensive so that the set 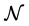 is much smaller than the set
is much smaller than the set 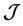 while the Hessians are even more restrictively used. In this paper, we use only data measurements such that
while the Hessians are even more restrictively used. In this paper, we use only data measurements such that  and
and . The correlation [8] function to be used is the Matern function
. The correlation [8] function to be used is the Matern function
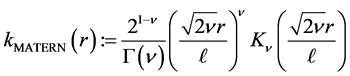 (13)
(13)
where 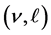 are positive hyper-parameters and
are positive hyper-parameters and 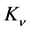 is the modified Bessel function. In dimension
is the modified Bessel function. In dimension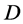 , the spectral density of the Matern function is
, the spectral density of the Matern function is
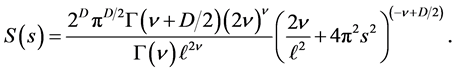 (14)
(14)
If 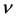 tends to infinity, one obtains the squared exponential case. For the special case of half-integers such as
tends to infinity, one obtains the squared exponential case. For the special case of half-integers such as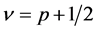 , one obtains a product of an exponential and a polynomial of order
, one obtains a product of an exponential and a polynomial of order 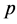 such that (13) becomes
such that (13) becomes
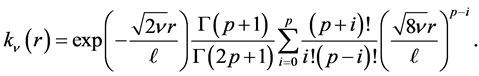 (15)
(15)
For the most applied cases where 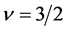 and
and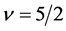 , one has
, one has
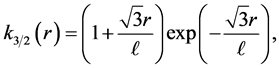 (16)
(16)
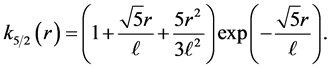 (17)
(17)
Suppose 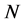 is the number of observations such that
is the number of observations such that 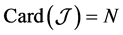 in (10). For noise-free observations, one has the covariance
in (10). For noise-free observations, one has the covariance
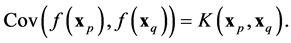 (18)
(18)
For a noisy data 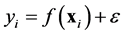 where the additional noise follows the Gaussian distribution
where the additional noise follows the Gaussian distribution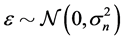 , the covariance becomes
, the covariance becomes
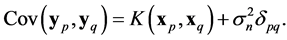 (19)
(19)
Let us denote the sampling points by 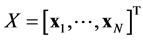 which is a matrix having the size
which is a matrix having the size 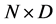 where
where 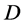 is the dimension of the trial variables
is the dimension of the trial variables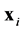 . The latent function and the set of observations are defined in a similar fashion such that
. The latent function and the set of observations are defined in a similar fashion such that 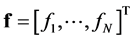 and
and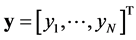 . The marginal likelihood is the integral of the likelihood and the prior such as
. The marginal likelihood is the integral of the likelihood and the prior such as
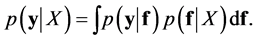 (20)
(20)
We denote by 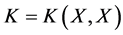 the covariance matrix whose entries are
the covariance matrix whose entries are 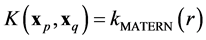 where
where 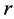 will be defined below as a generalized distance between
will be defined below as a generalized distance between 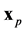 and
and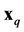 . We will use also
. We will use also 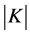 to denote the determinant of
to denote the determinant of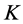 . If
. If 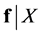 follows the Gaussian distribution
follows the Gaussian distribution 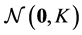 and one has no noise, then the marginal likelihood is
and one has no noise, then the marginal likelihood is
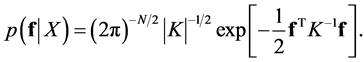 (21)
(21)
By taking the logarithm, the computation of the marginal likelihood is as follows
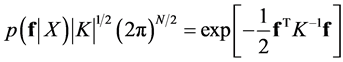 (22)
(22)
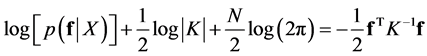 (23)
(23)
from which one obtains the log marginal likelihood
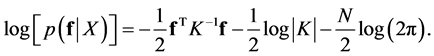 (24)
(24)
In the presence of noise 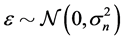 by using (19), the negative log marginal likelihood becomes
by using (19), the negative log marginal likelihood becomes
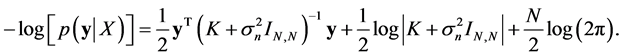 (25)
(25)
The first term 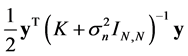 is the data-fit term while the second term
is the data-fit term while the second term 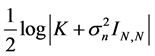 and the last term
and the last term 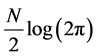 are respectively the complexity term and the normalization term. For a set of test points
are respectively the complexity term and the normalization term. For a set of test points
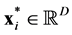 , the expressions
, the expressions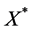 ,
, 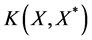 and
and 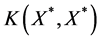 are defined in a similar way as
are defined in a similar way as  and
and . The predicted estimation follows the Gaussian distribution
. The predicted estimation follows the Gaussian distribution
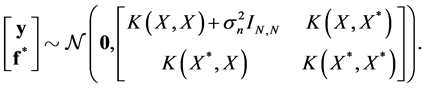 (26)
(26)
That is to say, for given 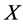 and
and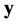 , the predictive distribution for a covariate vector
, the predictive distribution for a covariate vector 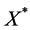 is a Gaussian admitting the following mean and variance
is a Gaussian admitting the following mean and variance
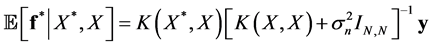 (27)
(27)
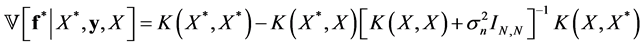 (28)
(28)
where those expressions are dependent on some set of hyper-parameters which we discuss below. The value of the generalized distance 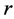 for given
for given 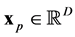 and
and 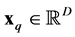 is
is
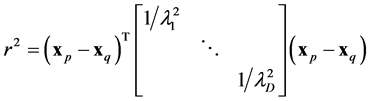 (29)
(29)
in which 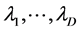 are related to hyper-parameters. In general, the set of hyperparameters include
are related to hyper-parameters. In general, the set of hyperparameters include 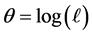 where
where 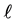 is from (16) and (17) as well as
is from (16) and (17) as well as 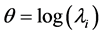 where
where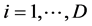 . The main objective is to determine the hyperparameters by optimizing the marginal likelihood. In practice, using the log marginal likelihood is more efficient to implement. In order to accelerate the speed of the nonlinear optimization, we need the gradients of the functional (25) with respect to the hyperparameters. For a hyper-parameter
. The main objective is to determine the hyperparameters by optimizing the marginal likelihood. In practice, using the log marginal likelihood is more efficient to implement. In order to accelerate the speed of the nonlinear optimization, we need the gradients of the functional (25) with respect to the hyperparameters. For a hyper-parameter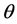 , one has the partial derivative
, one has the partial derivative
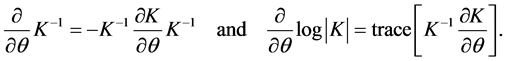 (30)
(30)
From the chain rule, one obtains
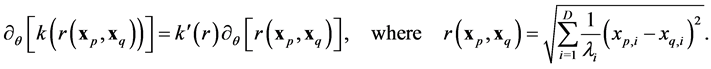 (31)
(31)
This is singular when 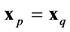 which occurs on the diagonal entries of the covariance matrix. In fact, one has
which occurs on the diagonal entries of the covariance matrix. In fact, one has
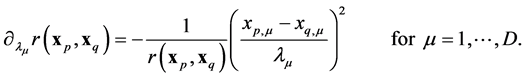 (32)
(32)
Working with 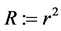 provides a regularization everywhere as
provides a regularization everywhere as 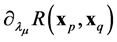 is regular. In addition,
is regular. In addition, 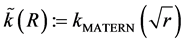 is smooth at the origin because one has indeed
is smooth at the origin because one has indeed 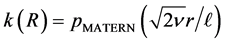 such that
such that
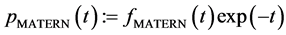 (33)
(33)
 (34)
(34)
where 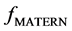 is a polynomial. In particular, for the cases where
is a polynomial. In particular, for the cases where 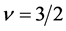 and
and 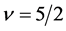 in (16) and (17), one has
in (16) and (17), one has 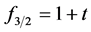 and
and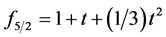 . In fact, one obtains the relation
. In fact, one obtains the relation
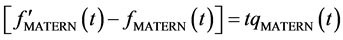 (35)
(35)
where 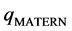 is a polynomial. Therefore, one deduces from (35)
is a polynomial. Therefore, one deduces from (35)
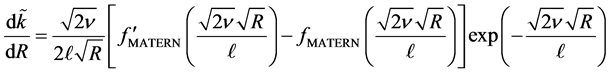 (36)
(36)
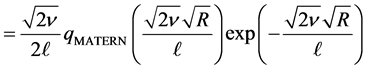 (37)
(37)
which is regular for all values of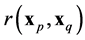 .
.
3. Simulation Results
In this section, we would like to report some results from computer simulation of the formerly described approach. First, we will present some results pertaining to general real valued multi-variate functions. That will be followed by some application in quantum simulation.
The former theoretical approach was implemented by using C/C++, BLAS/LAPACK and NLOPT. The BLAS packet is used for the fast vector operations. We use LAPACK for the linear operations such as Cholesky factorization and dense matrix solvers. We use NLOPT for the nonlinear operations for both the geometry optimization and the optimal hyper-parameters in the log marginal likelihood (25). NLOPT supports diverse nonlinear optimization operations [9] in which local optimizers are involved. A local one searches only inside a neighborhood of a certain provided starting initial guess. The optimizers are performed by using derivative free or gradient based algorithm which are available in NLOPT. Derivative free algorithms include BOBYQA (Bond Optimization BY Quadratic Approximation), COBYLA (Constrained Optimization BY Linear Approximation), NEWUOA (NEW Unconstrained Optimization Algorithm). Gradient-based methods include MMA (Method of Moving Asymptotes) and LBFGB (Limited memory Broyden-Fletcher-Goldfarb-Shanno). The code is a very developed version of the matlab implementation provided in [8] . The new additional enhancements from the matlab version consist of the following features. First, using NLOPT provides a lot of improvements as compared to the original matlab nonlinear conjugate gradients. That can be observed when both the number of points and the dimension become large in the nonlinear optimization of the hyper-parameters. In addition, we can also accept higher derivatives in the input apart from the functional values. One can use the entire gradient or only some components of it. Furthermore, the gradient of the kernel-based approximation can be evaluated. That can be done analytically instead of using finite difference. In addition, our C/C++ code admits some python interface enabling direct application to ATK which is the quantum package we use.
As a first test, we consider the reconstruction of the function 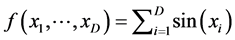 by using the kernel-based approximation. Since that function does not present any special feature such as cusp or boundary layer or any special interesting region, we use only randomly generated points. The initial guess of the hyper-parameters is provided by the users. One considers the determination of the final hyper-parameters as an unconstrained nonlinear optimization. The results of the computations are collected in Table 1 where the errors are computed for the function values as well as for the gradient values. The results exhibit the performance for different numbers of data for each dimension. In addition, we examine the effect of increasing the dimension
by using the kernel-based approximation. Since that function does not present any special feature such as cusp or boundary layer or any special interesting region, we use only randomly generated points. The initial guess of the hyper-parameters is provided by the users. One considers the determination of the final hyper-parameters as an unconstrained nonlinear optimization. The results of the computations are collected in Table 1 where the errors are computed for the function values as well as for the gradient values. The results exhibit the performance for different numbers of data for each dimension. In addition, we examine the effect of increasing the dimension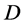 . In Figure 1(c), we display the error plots in function of the number of data. We consider dimensions
. In Figure 1(c), we display the error plots in function of the number of data. We consider dimensions 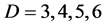 by analyzing the errors in the function evaluation. We observe that the increase of the dimension does not really deteriorate the accuracy too much. One needs certainly more points for higher dimensions but the increase of the number of additional points is not too significant.
by analyzing the errors in the function evaluation. We observe that the increase of the dimension does not really deteriorate the accuracy too much. One needs certainly more points for higher dimensions but the increase of the number of additional points is not too significant.
For the application to nano-simulation, we consider the unit cell generated by three vectors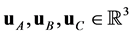 .
.
After a transformation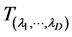 , they become
, they become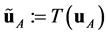 ,
, 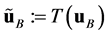 ,
,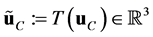 . For a bulk configuration
. For a bulk configuration 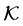 inside the unit cell, we denote by
inside the unit cell, we denote by 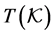 the transformed configuration where the fractional coordinates belonging to the transformed unit cell
the transformed configuration where the fractional coordinates belonging to the transformed unit cell 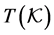 remain the same as in the original configuration
remain the same as in the original configuration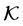 . Their values are within
. Their values are within 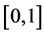 before and after the transformations. That is, the fractional coordinates of the reference configuration
before and after the transformations. That is, the fractional coordinates of the reference configuration 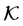 remain unchanged from beginning till the end of the computation. We are interested in the impact of the DFT energy by applying the transformation to the unit cell vectors. The transformation
remain unchanged from beginning till the end of the computation. We are interested in the impact of the DFT energy by applying the transformation to the unit cell vectors. The transformation 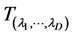 depends on
depends on 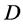 parameters so that the
parameters so that the 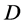 -variate function to be approximated maps
-variate function to be approximated maps 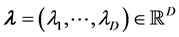 to the energy such as
to the energy such as
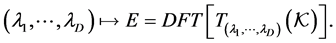
The first transformation consists of an isotropic one that corresponds to a unidimensional function which is a scaling. That transformation amounts to stretching and confining the unit cell equally in all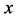 ,
, 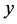 ,
, 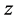 directions. Thus, the function to be approximated maps
directions. Thus, the function to be approximated maps 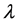 into
into 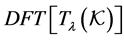 where one has
where one has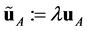 ,
,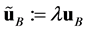 ,
,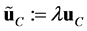 . The next transformations are anisotropic in the sense that the unit cell is scaled differently in the
. The next transformations are anisotropic in the sense that the unit cell is scaled differently in the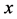 ,
,  ,
, 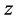 directions. The first anisotropic transformation scales in a way that
directions. The first anisotropic transformation scales in a way that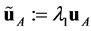 ,
, 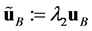 ,
,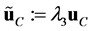 . That transformation corresponds to the case where the dimension is
. That transformation corresponds to the case where the dimension is 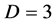 and
and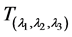 can be represented as a diagonal matrix having
can be represented as a diagonal matrix having 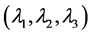 as entries. For the 2D anisotropic case, the transformation is given by
as entries. For the 2D anisotropic case, the transformation is given by 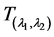 which has diagonal entries
which has diagonal entries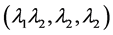 . For the most general transformation, one utilizes a strain tensor
. For the most general transformation, one utilizes a strain tensor
Table 1. Comparison w.r.t.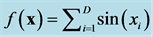 . Error of the function and gradient values on
. Error of the function and gradient values on 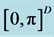 for dimension
for dimension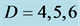 .
.
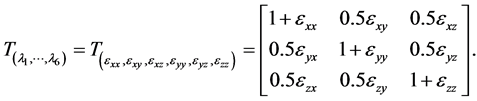 (38)
(38)
This is the Voigt strain tensor which is usually encountered in anisotropic transformations such as elasticity. This general transformation corresponds to a six-variate function since the Voigt strain matrix is supposed to be symmetric. The isotropic and 2D/3D anisotropic transformations are ensured to be non-singular, provided that the diagonal parameters are strictly positive. The tensor transformation in (38) is non-singular as long as the parameters 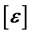 are not too large as the Voigt tensor approaches the identity transformation. Although we are interested in the general approximation of the quantum energy, we put more emphasis on the neighborhood of the position where the energy attains its minimal value because it defines the equilibrium of the system. The main objective is to obtain a good approximation next to the optimal point
are not too large as the Voigt tensor approaches the identity transformation. Although we are interested in the general approximation of the quantum energy, we put more emphasis on the neighborhood of the position where the energy attains its minimal value because it defines the equilibrium of the system. The main objective is to obtain a good approximation next to the optimal point 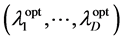 corresponding to
corresponding to
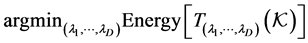 (39)
(39)
for a molecular or bulk configuration . We have built a function that performs the geometry optimization using unpolarized single
. We have built a function that performs the geometry optimization using unpolarized single  DFT calculators for any given molecular configuration. This is the first instance in the program where the optimizer NLOPT is applied. The Gaussian approximation are applied on a set of points
DFT calculators for any given molecular configuration. This is the first instance in the program where the optimizer NLOPT is applied. The Gaussian approximation are applied on a set of points
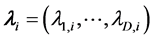 together with their images
together with their images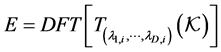 . In our applications, we accumulate very dense points in the neighborhood of the optimal value
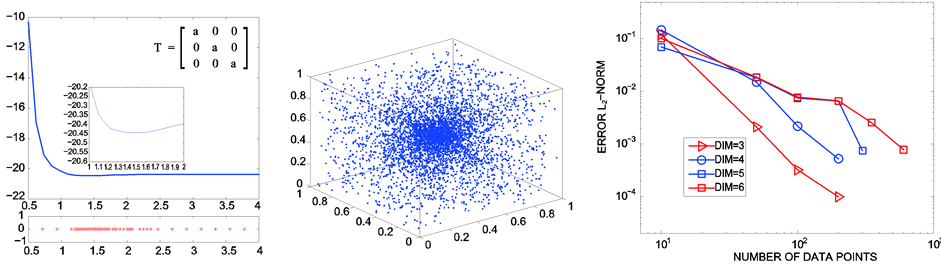
. In our applications, we accumulate very dense points in the neighborhood of the optimal value 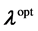 while only few points are used elsewhere. An illustration of this situation is displayed in Figure 1(a) for the unidimensional case where the energy curve is traced together with the samples accumulating at the equilibrium. A typical sampling point distribution for the spatial case is depicted in Figure 1(b). The implementation of the quantum application was realized by using ATK (Atomistix ToolKit) [10] [11] which consisted of python scripts. The ATK has some GUI extension well known as VNL (Virtual NanoLab). For given nuclei coordinates
while only few points are used elsewhere. An illustration of this situation is displayed in Figure 1(a) for the unidimensional case where the energy curve is traced together with the samples accumulating at the equilibrium. A typical sampling point distribution for the spatial case is depicted in Figure 1(b). The implementation of the quantum application was realized by using ATK (Atomistix ToolKit) [10] [11] which consisted of python scripts. The ATK has some GUI extension well known as VNL (Virtual NanoLab). For given nuclei coordinates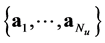 , that quantum packet can provide the energy
, that quantum packet can provide the energy 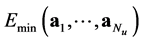 such that
such that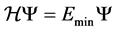 . As an example of using the ATK simulation, we observe the isosurface of the electron density function in Figure 2 for a composite system of germanium/silicon in which only the atoms inside the unit cell are displayed. The displayed figure corresponds to
. As an example of using the ATK simulation, we observe the isosurface of the electron density function in Figure 2 for a composite system of germanium/silicon in which only the atoms inside the unit cell are displayed. The displayed figure corresponds to 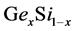 where
where 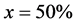 in a germanium-silicon combination obtained from a diamond structure. After applying the approach described in the previous sections to several atomic configurations, we collect the major results on Table 2. It mainly summarizes the elapsed time for the preparation and the performance of the new method. In the tabulated outcomes, we consider first Body Centered Cubic of germanium. In addition, we use composites which are labeled
in a germanium-silicon combination obtained from a diamond structure. After applying the approach described in the previous sections to several atomic configurations, we collect the major results on Table 2. It mainly summarizes the elapsed time for the preparation and the performance of the new method. In the tabulated outcomes, we consider first Body Centered Cubic of germanium. In addition, we use composites which are labeled 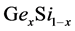 where
where 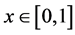 controls the amounts of germanium and silicon. More precisely, we consider the composites which are
controls the amounts of germanium and silicon. More precisely, we consider the composites which are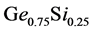 ,
, 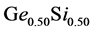 and
and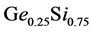 . All those composites are structured by using Face Centered Cubic as space group symmetry. The appropriate parameter values are obtained from the American Mineralogist Crystal Structure Database [12] .
. All those composites are structured by using Face Centered Cubic as space group symmetry. The appropriate parameter values are obtained from the American Mineralogist Crystal Structure Database [12] .
 (a) (b) (c)
(a) (b) (c)
Figure 1. Accumulated sampling points at the geometric optimum: (a) Unidimensional; (b)Tridimensional; (c) Increasing the dimensions.
 (a)
(a) (b)
(b)
Figure 2. Electronic density for the DFT simulation of composite germanium/silicon.
The preparation step consists of a geometry optimization and the determination of the kernel approximation. The duration of the Gaussian kernel is dominated by the DFT computations related to the point samples. The numbers of point samples are 70, 105, 200 and 250 for isotropic, 2D anisotropic, 3D anisotropic and Voigt tensor respectively. The stochastic computation as described in section 2.2 is very fast. In fact, the application of stochastic simulation is at most 2 percent of the whole preparation. All the computations were performed with the DFT basis unpolarized single 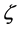 which is the least intensive basis available in the implementation. If other bases were used, the time for the DFT computation would last even much longer. In the case of DFT double
which is the least intensive basis available in the implementation. If other bases were used, the time for the DFT computation would last even much longer. In the case of DFT double 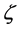 polarized, the scaling of the computation intensity might be doubled. In all dimensions, the preparation expense has long durations. Depending on the tensor transformation and the number of sample points, the preparation overhead can last a few minutes till several days. But the output of those preparations can be stored so that they need only be computed once for all. The ratio between the direct DFT-evaluation and the evaluation using kernel approximation is displayed in the last column of the Table 2. It exhibits that in average, the orders of acceleration are respectively
polarized, the scaling of the computation intensity might be doubled. In all dimensions, the preparation expense has long durations. Depending on the tensor transformation and the number of sample points, the preparation overhead can last a few minutes till several days. But the output of those preparations can be stored so that they need only be computed once for all. The ratio between the direct DFT-evaluation and the evaluation using kernel approximation is displayed in the last column of the Table 2. It exhibits that in average, the orders of acceleration are respectively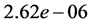 ,
, 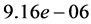 ,
, 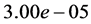 and
and 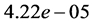 for the isotropic, 2D anisotropic, 3D anisotropic and 6D tensor cases. Since the acceleration advantage is very good, investing on the preparation process is worth calculating as the results can be stored and subsequently post-processed. In order to observe the improvement of the accuracy, we consider two silicon configurations in Figure 3. As a matter of fact, the first configuration consists of silicon admitting a hexagonal lattice using space group P63/mmc. The second one admits a Face Centered Cubic lattice possessing the space group Fd3m. For both configurations, the bond lengths are obtained from the American Mineralogist Crystal Structure Database [12] . They are respectively represented by triangular and circular marks on the diagonal. That figure displays a comparison of the accuracy between the DFT computation and the kernel approximation. Marks which are closer to the diagonal identify good agreements between the two methods. We present only the case of anisotropic 3D transformation in this comparison because the other cases would exhibit similar results. The only difference between the two figures is that more sample points are used for the second one. More precisely, 45 sampling points are used in the first simulation
for the isotropic, 2D anisotropic, 3D anisotropic and 6D tensor cases. Since the acceleration advantage is very good, investing on the preparation process is worth calculating as the results can be stored and subsequently post-processed. In order to observe the improvement of the accuracy, we consider two silicon configurations in Figure 3. As a matter of fact, the first configuration consists of silicon admitting a hexagonal lattice using space group P63/mmc. The second one admits a Face Centered Cubic lattice possessing the space group Fd3m. For both configurations, the bond lengths are obtained from the American Mineralogist Crystal Structure Database [12] . They are respectively represented by triangular and circular marks on the diagonal. That figure displays a comparison of the accuracy between the DFT computation and the kernel approximation. Marks which are closer to the diagonal identify good agreements between the two methods. We present only the case of anisotropic 3D transformation in this comparison because the other cases would exhibit similar results. The only difference between the two figures is that more sample points are used for the second one. More precisely, 45 sampling points are used in the first simulation
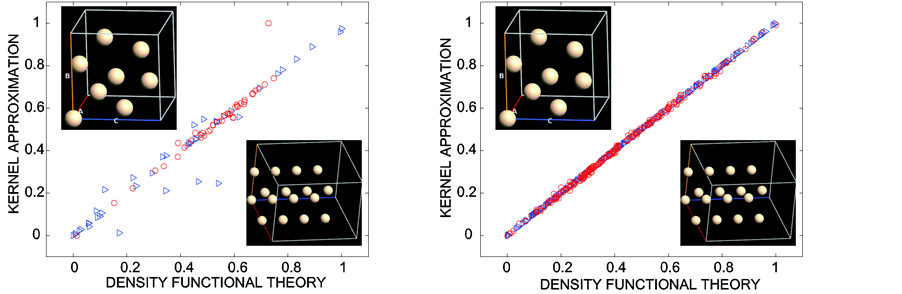 (a) (b)
(a) (b)
Figure 3. DFT vs. kernel approximation for two silicon configurations: (a) 45 sampling points; (b) 225 sampling points.
Table 2. Preparation overhead and acceleration gain.
while 225 are used for the second one. One can observe that the values on the diagonals become more precise as more sampling points are used. Additional sampling points can be used if a better accuracy is desired with the costs of having longer preparation overhead.
References
- Hill, J., Subramanian, L. and Maiti, A. (2005) Molecular Modeling Techniques in Material Sciences. Taylor & Francis Group, Boca Raton.
- Harbrecht, H. and Randrianarivony, M. (2011) Wavelet BEM on Molecular Surfaces: Solvent Excluded Surfaces. Computing, 92, 335-364. http://dx.doi.org/10.1007/s00607-011-0147-y
- Randrianarivony, M. (2013) On Space Enrichment Estimator for Nonlinear Poisson-Boltzmann. American Institute of Physics, 1558, 2365-2369.
- Randrianarivony, M. (2013) Parallel Processing of Analytical Poisson-Boltzmann Using Higher Order FEM. In: Klement, E.P., Borutzky, W., Fahringer, T., Hamza, M.H. and Uskov, V., Eds., Proceeding of Conference “Parallel and Distributed Computing and Networks”, ACTA Press, 455434, 1-6.
- Kohn, W. and Sham, L. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review, 140, 1133-11388. http://dx.doi.org/10.1103/PhysRev.140.A1133
- Perdew, J. and Wang, Y. (1992) Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Physical Review B, 45, 13244. http://dx.doi.org/10.1103/PhysRevB.45.13244
- Suryanarayana, P., Gavini, V., Blesgen, T., Bhattacharya, K. and Ortiz, M. (2010) Non-Periodic Finite-Element Formulation of Kohn-Sham Density Functional Theory. Journal of the Mechanics and Physics of Solids, 58, 256-280. http://dx.doi.org/10.1016/j.jmps.2009.10.002
- Rasmussen, C. and Williams, C. (2006) Gaussian Processes for Machine Learning. The MIT Press, Massachusetts.
- Johnson, S. (2010) The NLopt Nonlinear Optimization Package. http://ab-initio.mit.edu/nlopt
- Atomistix ToolKit Version 13.8.0, QuantumWise A/S. www.quantumwise.com
- Brandbyge, M., Mozos, J., Ordejon, P., Taylor, J. and Stokbro, K. (2002) Density-Functional Method for Nonequilibrium Electron Transport. Physical Review B, 65, 165401. http://dx.doi.org/10.1103/PhysRevB.65.165401
- American Mineralogist Crystal Structure Database. http://rruff.geo.arizona.edu/AMS/


