Advances in Materials Physics and Chemistry
Vol. 2 No. 3 (2012) , Article ID: 23177 , 11 pages DOI:10.4236/ampc.2012.23017
The STM Images of Pt (111) (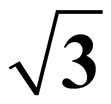 ×
× )R30˚/CO Surface by DFT Calculations
)R30˚/CO Surface by DFT Calculations
Industrial Technology Research Institute, Zhejiang University, Hangzhou, China
Email: zdcixijishu@zju.edu.cn
Received June 19, 2012; revised July 19, 2012; accepted August 3, 2012
Keywords: Pt (111) ( 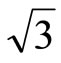 ×
×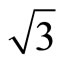 )R30˚/CO surface; STM image; Chemisorption
)R30˚/CO surface; STM image; Chemisorption
ABSTRACT
In this work we have performed total-energy calculations of the chemisorption properties and STM images of Pt (111) ( ×
×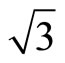 )R30˚/CO surface by using the density functional theory (DFT) and the projector-augmented wave (PAW) method. The calculations show that carbon monoxide molecule (CO) adsorbs on FCC site in the Pt (111) (
)R30˚/CO surface by using the density functional theory (DFT) and the projector-augmented wave (PAW) method. The calculations show that carbon monoxide molecule (CO) adsorbs on FCC site in the Pt (111) (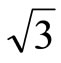 ×
×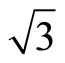 )R30˚ surface is energetically favored by the GGA-PBE XC-functional, this is in agreement with most of the theoretical calculations which is using different XC-functional at the most. However, these results strongly conflicted with the existing experiments. Actually the calculated workfunction for the FCC adsorption is quite different from the experiments while the atop one is in good agreement with experiments. We speculate that the atop adsorption for (
)R30˚ surface is energetically favored by the GGA-PBE XC-functional, this is in agreement with most of the theoretical calculations which is using different XC-functional at the most. However, these results strongly conflicted with the existing experiments. Actually the calculated workfunction for the FCC adsorption is quite different from the experiments while the atop one is in good agreement with experiments. We speculate that the atop adsorption for (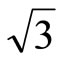 ×
×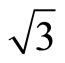 )R30˚/CO is favorable for the adsorption case at the most. Furthermore, we have calculated the scanning tunneling microscopy (STM) images for both adsorption geometries and suggest that there should be existed remarkable differences in the STM images. The present work provides a faithful criterion accounting for the local surface geometry in Pt (111) (
)R30˚/CO is favorable for the adsorption case at the most. Furthermore, we have calculated the scanning tunneling microscopy (STM) images for both adsorption geometries and suggest that there should be existed remarkable differences in the STM images. The present work provides a faithful criterion accounting for the local surface geometry in Pt (111) (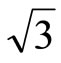 ×
× )R30˚/CO surface from surface workfunctions and STM images instead of total-energy calculations.
)R30˚/CO surface from surface workfunctions and STM images instead of total-energy calculations.
1. Introduction
CO adsorption is an important mechanistic step in the chemical reaction pathway of many heterogeneous catalytic reactions [1]. In these catalytic reactions, transition metals play a dominate role in considerably enhancing the rate of reaction that involves the adsorption, diffusion and bond dissociation steps of carbon monoxide [2]. One of the important examples is the adsorption of CO on the Pt (111) surface due to the high economic and environmental implications in materials science [3]. The process is not simple and still generating challenges to experimentalists and theoreticians; especially the site that is occupied by the CO molecule has triggered a huge interest in the community of those performing ab-initio calculations. Particularly for Pt (111) (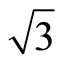 ×
×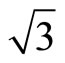 )R30˚ attentionem, it has attracted considerable attentions in the past decade. For sub-saturation CO coverage, small (
)R30˚ attentionem, it has attracted considerable attentions in the past decade. For sub-saturation CO coverage, small (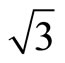 ×
× )R30˚/CO islands were observed in the experiments [4,5]. Under a proper coverage and heat treatment, these islands can display a strong tendency to align to form long equally spaced chains of islands separated by areas of the clean Pt (111) surface [6]. Thus, these mesoscopic orderings in early scanning tunneling microscopy (STM)
)R30˚/CO islands were observed in the experiments [4,5]. Under a proper coverage and heat treatment, these islands can display a strong tendency to align to form long equally spaced chains of islands separated by areas of the clean Pt (111) surface [6]. Thus, these mesoscopic orderings in early scanning tunneling microscopy (STM)
and its consequent potential as a template for nano-scaled over layer structure formation demand more researches. It is generally accepted that the ordering of the (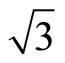 ×
×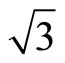 ) R30˚/CO phase, having a typical dimension, is driven by long-range elastic forces arising from compressive surface stress in the islands and tensile surface stress in the intervening areas of clean surfaces. However, the detailed local structure within the (
) R30˚/CO phase, having a typical dimension, is driven by long-range elastic forces arising from compressive surface stress in the islands and tensile surface stress in the intervening areas of clean surfaces. However, the detailed local structure within the (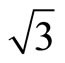 ×
×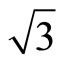 )R30˚/CO domains have continued to be unsolved. Experiments have indicated that at low coverage CO prefers to adsorb at the atop sites on the Pt (111) (
)R30˚/CO domains have continued to be unsolved. Experiments have indicated that at low coverage CO prefers to adsorb at the atop sites on the Pt (111) (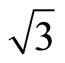 ×
×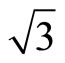 )R30˚ surface measured by low-energy electron diffraction (LEED) [7,8] as well as electron energy-loss spectroscopy (EELS) [7,9]. moreover, Blackman et al. [10] Have reported that at one-third of a monolayer of CO on Pt (111) at 160 K, (88 ± 5)% of the molecules are found to occupy top sites and (12 ± 5)% bridge sites by using Diffuse-LEED. This result is consistent with the HREELS experiment [7]. While the infrared reflection absorption spectroscopy results have shown that only one adsorption site at coverage ≤ 3.3 ML [11].
)R30˚ surface measured by low-energy electron diffraction (LEED) [7,8] as well as electron energy-loss spectroscopy (EELS) [7,9]. moreover, Blackman et al. [10] Have reported that at one-third of a monolayer of CO on Pt (111) at 160 K, (88 ± 5)% of the molecules are found to occupy top sites and (12 ± 5)% bridge sites by using Diffuse-LEED. This result is consistent with the HREELS experiment [7]. While the infrared reflection absorption spectroscopy results have shown that only one adsorption site at coverage ≤ 3.3 ML [11].
Using density-functional theory (DFT) method, most of the calculations [12] have admitted that the FCC sites are the most stable adsorption sites. The different viewpoints between theories and experiments have been undergone for many years. It is generally acknowledged that DFT can’t get the correct adsorbent sites of CO molecules adsorption on Pt (111) (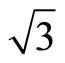 ×
×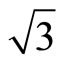 )R30˚ surface. Recently, Doll [13] using B3LYP XC-functional has supported that the adsorption energy of atop sites was larger than fcc sites. Though this result is in line with the experiments, it can’t be accepted fundamentally on the grounds of PBE-XC as the most accurate way. Some people even consider that B3LYP should not calculate bulk metals or metal surfaces. In order to deal with the disagreements of the adsorption sites of Pt (111) (
)R30˚ surface. Recently, Doll [13] using B3LYP XC-functional has supported that the adsorption energy of atop sites was larger than fcc sites. Though this result is in line with the experiments, it can’t be accepted fundamentally on the grounds of PBE-XC as the most accurate way. Some people even consider that B3LYP should not calculate bulk metals or metal surfaces. In order to deal with the disagreements of the adsorption sites of Pt (111) (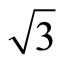 ×
×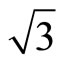 )R30˚/CO surface within experiments and theories, we have performed total-energy calculations on the chemisorption properties and STM images of Pt (111) (
)R30˚/CO surface within experiments and theories, we have performed total-energy calculations on the chemisorption properties and STM images of Pt (111) ( ×
× )R30˚/CO surface by using the DFT and the projector-augmented wave (PAW) method. In all, we have suggested that the surface workfunctions can be used to confirm the perfect adsorption site distinctly. A serial of Pt (111) (
)R30˚/CO surface by using the DFT and the projector-augmented wave (PAW) method. In all, we have suggested that the surface workfunctions can be used to confirm the perfect adsorption site distinctly. A serial of Pt (111) ( ×
×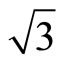 )R30˚/CO STM images for different sample bias, tip heights and absorbed sites are also simulated.
)R30˚/CO STM images for different sample bias, tip heights and absorbed sites are also simulated.
2. Methodology
In present work the calculations are performed using the DFT in the implementation of the PAW method proposed by Blöchl [14]. The exchange-correlation functional is treated within the general gradient approximation (GGA) [15,16]. The Kohn-Sham equations are solved by applying the Vienna ab-initio Simulation Package (VASP) [17,18], which is a complex package for performing ab-initio quantum-mechanical molecular dynamics (MD) simulations using ultrasoft pseudo-potentials (USPP) [19] or PAW method [14,17] and a plane wave basis set. Here, we have adopted the VASP dataset of PAW method since the PAW method is more accurate than the USPP dataset [20].
The Pt (111) (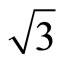 ×
×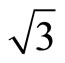 )R30˚/CO surface is simulated by seven layers of Pt (111) plane with a ~ 10.0 Å vacuum region, which is sufficient to avoid interferences between atoms from different slabs by convergence test. The bottom four layers of Pt (111) plane are fixed in bulk positions in order to provide an environment of bulk Pt substrate. An isolated CO molecule is adsorbed on one side of the substrate. The sampling k-point set was generated automatically in the approach of Monkhorst-Pack [21] and the k-mesh are fixed to be 16 × 16 × 1 and 8 × 8 × 1 for p (1 × 1) and (
)R30˚/CO surface is simulated by seven layers of Pt (111) plane with a ~ 10.0 Å vacuum region, which is sufficient to avoid interferences between atoms from different slabs by convergence test. The bottom four layers of Pt (111) plane are fixed in bulk positions in order to provide an environment of bulk Pt substrate. An isolated CO molecule is adsorbed on one side of the substrate. The sampling k-point set was generated automatically in the approach of Monkhorst-Pack [21] and the k-mesh are fixed to be 16 × 16 × 1 and 8 × 8 × 1 for p (1 × 1) and ( ×
×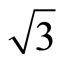 )R30˚ periodic surfaces, respectively. Test calculations with cut-off energies up to 500 eV and with different numbers of sampling k-points are employed and obtained total energy of adsorbed surface within 0.001 eV [22]. Optimization of the atomic structures was performed for each surface system via a conjugate-gradient (CG) algorithm [23] using the total energy and the Hellmann-Feynman forces on the atoms. The convergence criteria for total energy and the HellmannFeynman force are taken as 10−5 eV and 10−3 eV/Å, respectively. In addition, the polarization correction has been considered along the direction perpendicular to Pt (111) layers. Our calculated the lattice constant of the bulk platinum (~3.99 Å) is in good agreement with experiment (~3.92 Å) [24],which is ~1.7% larger than the measured value. Meanwhile, a p (1 × 1) periodic cell was chose to discuss the atomic relaxation of the clean Pt (111) surface.
)R30˚ periodic surfaces, respectively. Test calculations with cut-off energies up to 500 eV and with different numbers of sampling k-points are employed and obtained total energy of adsorbed surface within 0.001 eV [22]. Optimization of the atomic structures was performed for each surface system via a conjugate-gradient (CG) algorithm [23] using the total energy and the Hellmann-Feynman forces on the atoms. The convergence criteria for total energy and the HellmannFeynman force are taken as 10−5 eV and 10−3 eV/Å, respectively. In addition, the polarization correction has been considered along the direction perpendicular to Pt (111) layers. Our calculated the lattice constant of the bulk platinum (~3.99 Å) is in good agreement with experiment (~3.92 Å) [24],which is ~1.7% larger than the measured value. Meanwhile, a p (1 × 1) periodic cell was chose to discuss the atomic relaxation of the clean Pt (111) surface.
3. Calculated Results
3.1. Calculated Properties of Clean Pt (111) Surface
Usually a clean Pt (111) surface occurs only a structural relaxation instead of a reconstruction, i.e., the surface atoms move a little perpendicularly. In this article we have optimized the structural configuration for a clean Pt (111) surface with relaxations by using CG procedure and total-energy calculations. The relaxation for the outmost layers of Pt (111) surface are Dd12/d0 = +1.01%, Dd23/d0 = −0.25%, and Dd34/d0 = −0.26%, respectively, where minus means a surface contraction while plus the surface expansion. Our calculations combined with previous calculations and experiments for the surface relaxation of clean Pt (111) are summarized in Table 1. Our calculated surface relaxation Dd12/d0 = +1.01% locates well within the experimental ranges [25,26]. The other previous experiments [27,28] on the surface relaxation Dd12/d0 were less than 1.1%. It is noticed that the DFT calculations based on PW91 type GGA [29] yielded a very similar surface relaxation with ours. While, the calculation using the B3LYP XC-functional [13] obtained a larger surface expansion (~2.2%). For the relaxations of the second and third Pt (111) layers, the theoretical results were shown to be very small (<0.5%). Actually most of the experiments [25,27,28] have shown similar results on this issue. The atomic relaxations of Pt (111) surface in this work are agree well with all the existing calculations and experiments both quantitatively and qualitatively. By the way, the surface expansion of Pt (111) surface is in contrast to Cu (111), Ag (111), and Ni (111) surface [30], which relax slightly inwards [31] and where the Mulliken charge is slightly positive in the outermost layer [28].
The surface energy of Pt (111) surface is obtained from the total-energy calculations of bulk platinum and the relaxed Pt (111) surface. The detailed procedures are outlined as follows: firstly the total energy of a platinum atom in a bulk material was calculated, say Ebulk; and then the total energy of a relaxed surface slab (Eslab) with p (1 × 1) periodicity including N layers of Pt (111) sur
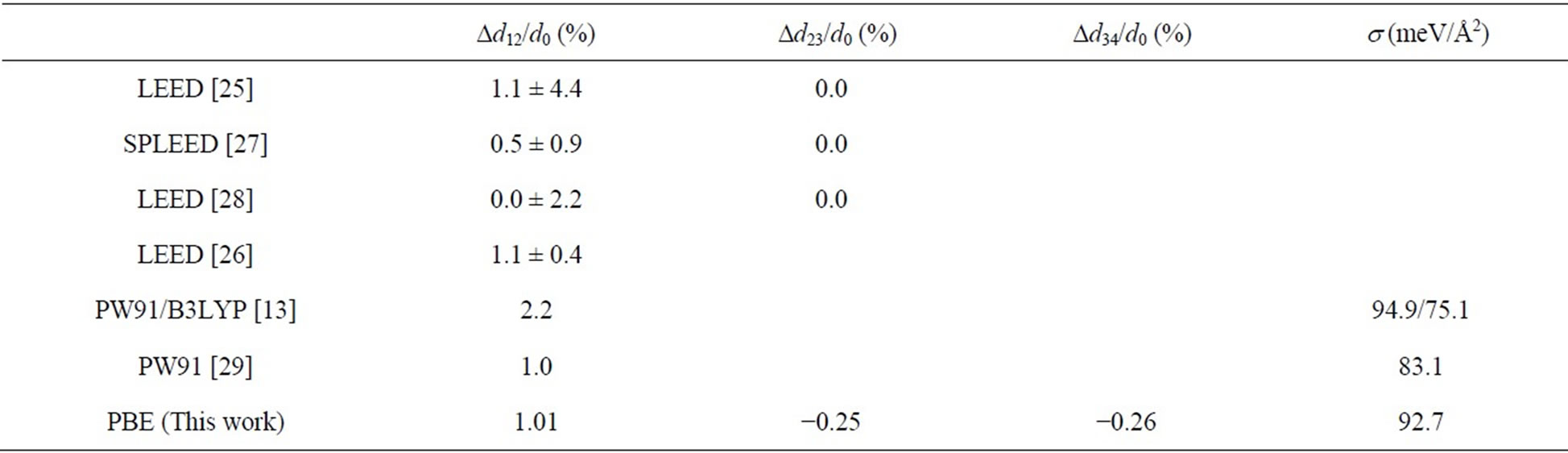
Table 1. Experimental vs PBE method about the relaxations for the surface layers and surface energy s (d0 is the distance between C over layer and topmost Pt layer. Ddij/d0 are the relative variations of layer spacing and the indexes indicate the corresponding substrate atomic layer).
face was computed; Finally the surface energy s can be determined in the following formula:

where N = 7, and A is the surface area of a p (1 × 1) slab cell. The s was calculated to be ~92.7 meV/Å2 by using PBE exchange-correlation functional in present work. Doll et al. [13] have reported the surface energy of Pt (111) surface to be ~94.9 meV/Å2 and ~75.1 meV/Å2 by using PW91 and B3LYP XC-functional, respectively. Moreover, Crljen et al. [29] have obtained the value of this surface energy ~83.1 meV/Å2. The present results on surface energy for Pt (111) and related calculations are listed and summarized in Table 1 for comparison. Finally, these observations show that the calculated results in this paper are reliable and reasonable.
3.2. Adsorption properties of CO on Pt (111) (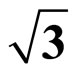 ×
×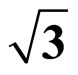 )R30˚ surface
)R30˚ surface
Two possible structures of Pt (111) ( ×
×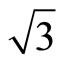 )R30˚/CO surface have been performed by geometry optimizations and total-energy calculations. In this section we pay attentions to the atomic and adsorption properties of Pt (111) (
)R30˚/CO surface have been performed by geometry optimizations and total-energy calculations. In this section we pay attentions to the atomic and adsorption properties of Pt (111) (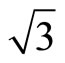 ×
×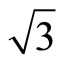 )R30˚/CO surface. The adsorption energy is defined as the difference between the total energy of a gas-phase CO molecule plus clean Pt (111) surface slab and the total energy of adsorbate-adsorbent system:
)R30˚/CO surface. The adsorption energy is defined as the difference between the total energy of a gas-phase CO molecule plus clean Pt (111) surface slab and the total energy of adsorbate-adsorbent system:

In Table 2 the adsorption energies of upright CO adsorption on Pt (111) (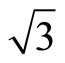 ×
×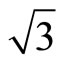 )R30˚ surface reported in previous calculations [12] and the present results are compiled for comparison. It is found that the Eads depends strongly on the form of XC-functional. As shown in Table 2, the adsorption energies with various adsorption sites employed by PBE and PW91 [13] XC-functional yielded a similar order (Eads for hollow sites > atop sits). While, the results using RPBE [12] and B3LYP [13] XC-functional predicted that a peak value occurs on atop site. Doll et al. [13] have suggested that the inversion on the adsorption energies could be obtained if the B3LYP XC-functional was used instead of PBE XC-functional.
)R30˚ surface reported in previous calculations [12] and the present results are compiled for comparison. It is found that the Eads depends strongly on the form of XC-functional. As shown in Table 2, the adsorption energies with various adsorption sites employed by PBE and PW91 [13] XC-functional yielded a similar order (Eads for hollow sites > atop sits). While, the results using RPBE [12] and B3LYP [13] XC-functional predicted that a peak value occurs on atop site. Doll et al. [13] have suggested that the inversion on the adsorption energies could be obtained if the B3LYP XC-functional was used instead of PBE XC-functional.
In our work, the Eads of upright CO molecule on the three symmetric sites of Pt (111) surface were calculated in details, i.e., 1.66 eV for fcc hollow, 1.64 eV for hcp hollow, and 1.54 eV for atop sites, respectively (Figure 1). It should be noted that the adsorption energy of hollow sites is ~0.10 eV larger than that of atop site. Actually the difference among adsorption energies with various adsorption sites is very quite small. In partially previous PBE calculation yielded a maximum difference ~ 0.27 eV, while in present work it was reduced considerably ~0.12 eV.
As a matter of fact, the RPBE and B3LYP XC-functionals could recover proper CO adsorption site on Pt (111) (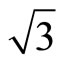 ×
×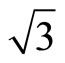 )R30˚/CO surface, while the PBE XC-functional could still yields a good description on the charge density and local electronic potential. Actually PBE and B3LYP are two different exchange-correlation functions: B3LYP, an exchange functional where the
)R30˚/CO surface, while the PBE XC-functional could still yields a good description on the charge density and local electronic potential. Actually PBE and B3LYP are two different exchange-correlation functions: B3LYP, an exchange functional where the
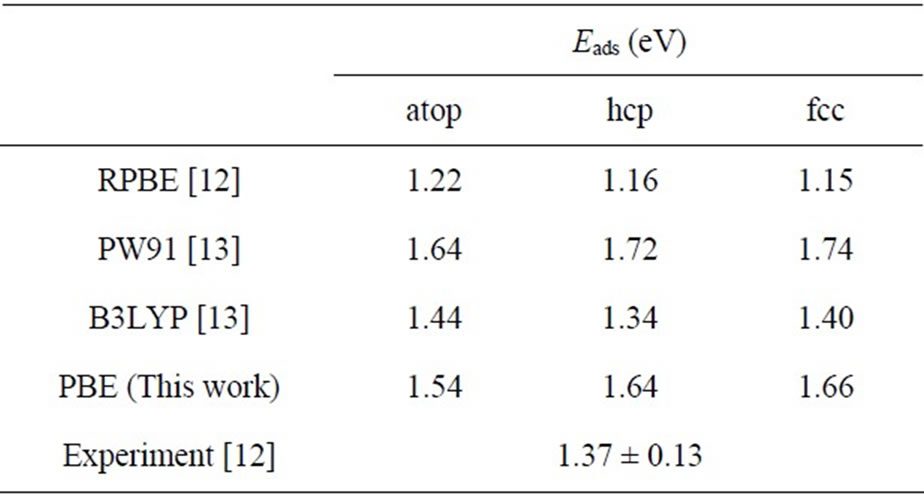
Table 2. Calculated adsorption energy (Eads) of Pt (111) ( ×
× )R30˚/CO surface.
)R30˚/CO surface.

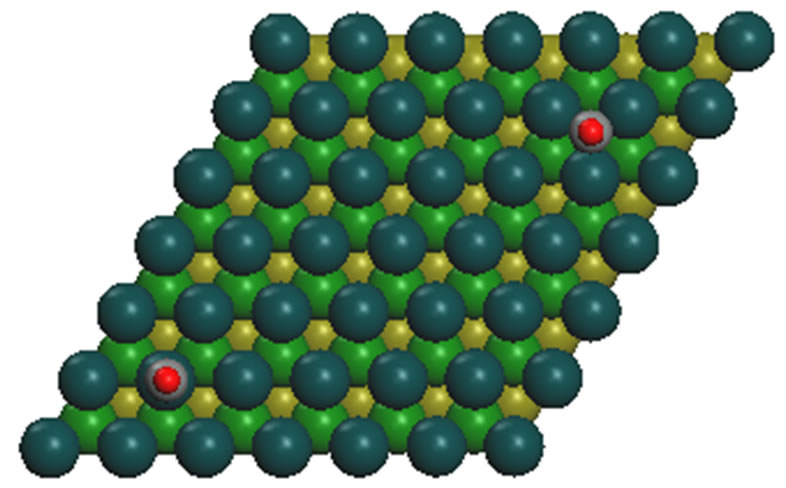
Figure 1. It displays the conventional (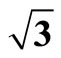 ×
×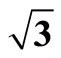 )R30˚ reconstruction on the Pt (111)/CO surface, i.e., the adsorbate on the left occupy on atop site at the coverage of 0.33 ML. It is a another possible adsorption geometry on the right in which the carbon atom and oxygen atom stay on the fcc of the outmost Pt atoms with the same periodicity (
)R30˚ reconstruction on the Pt (111)/CO surface, i.e., the adsorbate on the left occupy on atop site at the coverage of 0.33 ML. It is a another possible adsorption geometry on the right in which the carbon atom and oxygen atom stay on the fcc of the outmost Pt atoms with the same periodicity (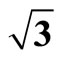 ×
×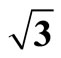 ) R30˚.
) R30˚.
parameter were fitted to experimental molecular data [32]. This correlation functional is not based on the Local-density-approximate (LDA) [33] which was widely used by physics community. It has been derived as an extension to other closed-shell systems of the ColleSalvetti expression [34] for the electronic correlation in helium. Therefore, B3LYP is more extensively used by chemists. PBE is a popular exchange correlation in the physics community and was derived as an exchange and correlation functional that satisfies as many formal properties and limits as possible, sacrificing only those deemed to be energetically less important. The PBE functional is a very satisfactory XC-functional from the theoretical point of view, because it verifies many of the exact conditions for the XC hole, and it does not contain any fitting parameters. In addition, its quality is equivalent to or even better than BLYP XC-functional in the case of Pt (111) (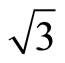 ×
×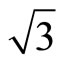 )R30˚ surface. In consideration of above reasons, we think that the existing XC-functional could predict preferred CO adsorption site in Pt (111) (
)R30˚ surface. In consideration of above reasons, we think that the existing XC-functional could predict preferred CO adsorption site in Pt (111) ( ×
× )R30˚ surface. Moreover, since the difference of charge density and local energy caused by different XC-functional is very small, the PBE type XCfunctional could generate a charge density and energy distribution very close to that of B3LYP. Therefore, we could calculate some interesting properties such as electric potential, charge density, and STM image using PBE XC-functional in the case of CO adsorption even though the PBX type XC-functional could not predict the proper adsorption site.
)R30˚ surface. Moreover, since the difference of charge density and local energy caused by different XC-functional is very small, the PBE type XCfunctional could generate a charge density and energy distribution very close to that of B3LYP. Therefore, we could calculate some interesting properties such as electric potential, charge density, and STM image using PBE XC-functional in the case of CO adsorption even though the PBX type XC-functional could not predict the proper adsorption site.
Next we focus on the workfunctions of the clean and adsorded Pt (111) ( ×
× )R30˚ surfaces. The surface workfunction for a clean and relaxed Pt (111) (
)R30˚ surfaces. The surface workfunction for a clean and relaxed Pt (111) ( ×
×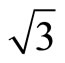 )R30˚ surface was calculated to be 5.72 eV, which coincides with the experiment ~5.93 eV [35]. In the case of Pt (111) (
)R30˚ surface was calculated to be 5.72 eV, which coincides with the experiment ~5.93 eV [35]. In the case of Pt (111) (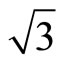 ×
×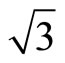 )R30˚/CO surface, the calculated results of workfunction have been tabulated and comprised with previous studies in Table 3. It is noted that the workfunction of atop adsorption (~5.68 eV) calculated in present work is very close to the experiment (~ 5.70 eV) [36]. While the change of workfuncion for fcc and hcp sites adsorptions enhanced by ~1.1 eV relative to the experimental value. Furthermore, the average electric potential along the z-axis for the fcc and atop adsorptions on Pt (111) (
)R30˚/CO surface, the calculated results of workfunction have been tabulated and comprised with previous studies in Table 3. It is noted that the workfunction of atop adsorption (~5.68 eV) calculated in present work is very close to the experiment (~ 5.70 eV) [36]. While the change of workfuncion for fcc and hcp sites adsorptions enhanced by ~1.1 eV relative to the experimental value. Furthermore, the average electric potential along the z-axis for the fcc and atop adsorptions on Pt (111) (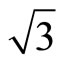 ×
×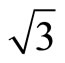 )R30˚/CO surface are plotted in Figure 2. Though the PBE XC-functional could not predict correct total energy tendency among the three symmetric adsorption sites of Pt (111) (
)R30˚/CO surface are plotted in Figure 2. Though the PBE XC-functional could not predict correct total energy tendency among the three symmetric adsorption sites of Pt (111) (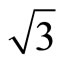 ×
× )R30˚/CO surface, the PBE still could be used to discuss properties related to local electric potential and charge density with a very small difference (see Figure 2 in detailed). Thus, we have suggested a very important point that workfunction could be used as a powerful tool to determine the CO adsorption site in Pt (111) (
)R30˚/CO surface, the PBE still could be used to discuss properties related to local electric potential and charge density with a very small difference (see Figure 2 in detailed). Thus, we have suggested a very important point that workfunction could be used as a powerful tool to determine the CO adsorption site in Pt (111) (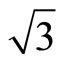 ×
×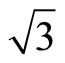 )R30˚/CO system.
)R30˚/CO system.
Finally, the calculated structural parameters of adsorbed CO are listed in Table 4. In the Table symbol RC-O is the distance between carbon and oxygen atoms and the RC-Sub is the perpendicular distance between carbon and the topmost Pt (111) layer. It is noticed that our results are identical well with previous experiments and calculations. Actually, the RC-Sub ~ 2.04 Å in atop adsorption obtained in this work could be viewed as a better prediction if considering about the hardness of carbon atom and the radius of platinum atom. Theoretically the summation of covalent radii of carbon and platinum is
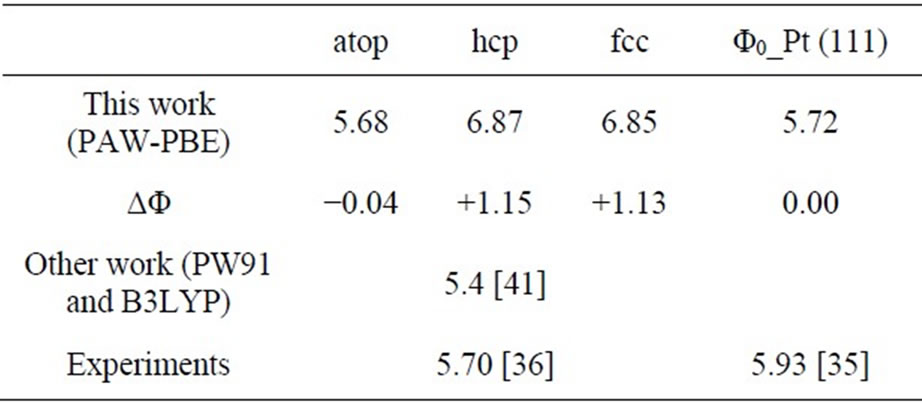
Table 3. Calculated workfunction (Φ) of Pt (111) (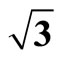 ×
×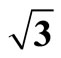 )R30˚/CO surface and the difference of such a adsorbed surface relative to a clean Pt (111) surface (Φ0), the difference is defined as ΔΦ (=Φ − Φ0), while the unit of workfunction is in eV.
)R30˚/CO surface and the difference of such a adsorbed surface relative to a clean Pt (111) surface (Φ0), the difference is defined as ΔΦ (=Φ − Φ0), while the unit of workfunction is in eV.
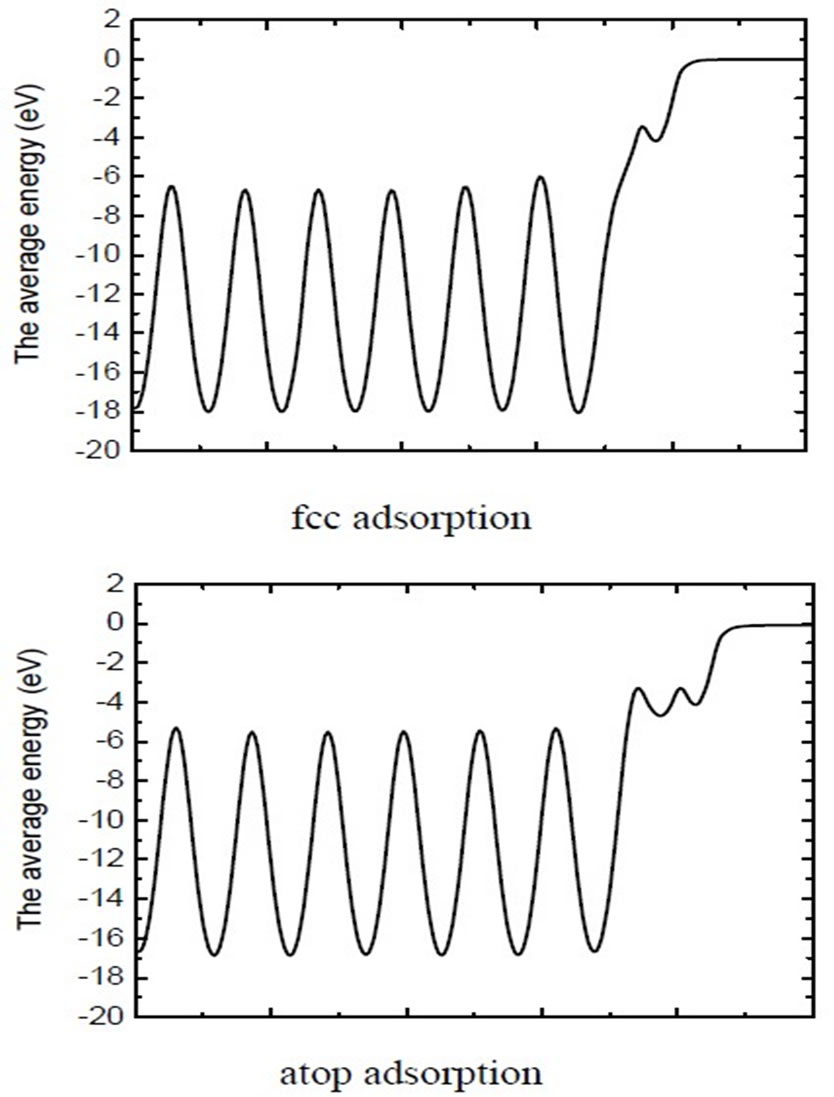
Figure 2. The average electric potential along the z-axis for both fcc hollow site and atop adsorption on Pt (111) (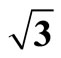 ×
×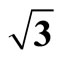 )R30˚/CO surface. (The vacuum energy level is set to 0.0). Left panel: fcc hollow site adsorption; Right panel: atop site adsorption.
)R30˚/CO surface. (The vacuum energy level is set to 0.0). Left panel: fcc hollow site adsorption; Right panel: atop site adsorption.
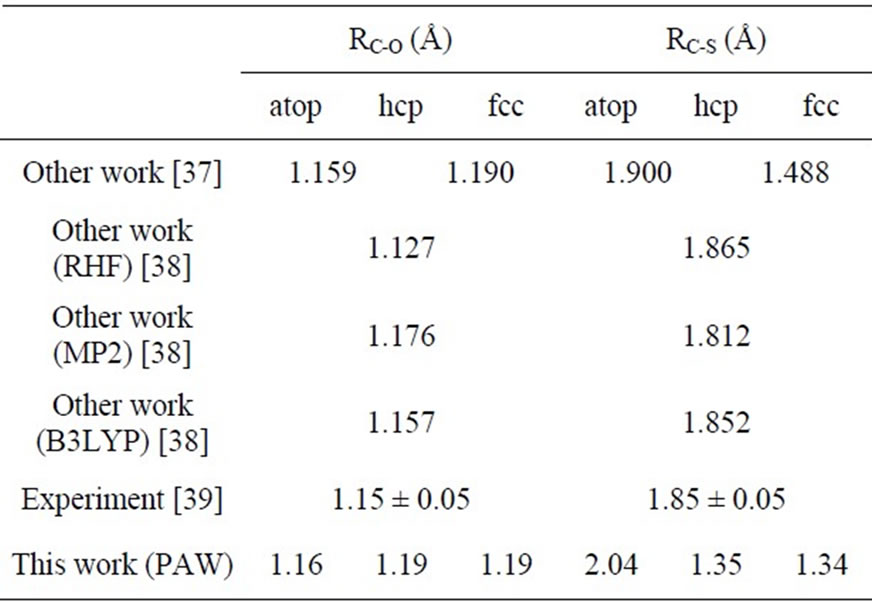
Table 4. Theoretical calculated and experimental bond lengths of carbon monoxide RC-O, and related perpendicular distance between carbon and Pt substrate RC-S in Pt (111) (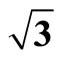 ×
×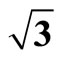 )R30˚/CO surface.
)R30˚/CO surface.
about 2.15 Å. If the charge transfer between carbon and oxygen is included, the reduction of RC-Sub from 2.15 Å to 2.04 Å is naturally acceptable.
3.3. The Simulated STM Line Scans from the First-Principles Approach
The STM has evolved into a very powerful tool for the understanding of adsorption structures on surface. Until now, the adsorption of CO on Pt (111) c (4 × 2) surface at 0.5 ML with variable temperature STM have been studied by Pedersen et al. [40] In this section we focus on the simulated STM line scans for the Pt (111) (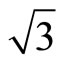 ×
× )R30˚/CO surface with 0.33 ML from the first-principles method and Tersoff-Hamann approach [42]. We have performed a structural relaxation in this configuration yet. In this model the adsorbed carbon and oxygen atoms reside at the levels higher than Pt atoms and thus these CO molecules were considered as the protrusions in STM image (see Figure 1). In this calculation the effect contributed by the STM tip was ignored and the STM image is of four-fold symmetry. Since STM is mostly used in the constant-current mode, and the corrugation of the tip is the quantity which is most suitable to make contact with experiments. Here, we have calculated the bias range from −0.6 to +0.2 V with the tip height ~ 5.0 and 5.5 Å. In practice the tip height is hard to determine by direct way. Usually in the constant-current mode the average tip height corresponds to a certain tunnel-current and the negative bias corresponds to the occupied states on the surface in STM experiments. In Figures 3 and 4, a serial of typical corrugation topography for different sample bias, tip heights and absorbed sites were presented. In the two-dimensional (2D) images (left part of Figures 3 and 4), the black areas represent the low corrugation amplitude of tip and the white plots represent the high corrugation amplitude of tip. The right parts of Figures 3 and 4 are three-dimensional (3D) color surfaces with corrugation images. Actually the section of such 3D surface could be viewed as the line scan along certain path on the surface. The simulated STM line scans employed within Tersoff–Hamann approach show that the Pt (111) (
)R30˚/CO surface with 0.33 ML from the first-principles method and Tersoff-Hamann approach [42]. We have performed a structural relaxation in this configuration yet. In this model the adsorbed carbon and oxygen atoms reside at the levels higher than Pt atoms and thus these CO molecules were considered as the protrusions in STM image (see Figure 1). In this calculation the effect contributed by the STM tip was ignored and the STM image is of four-fold symmetry. Since STM is mostly used in the constant-current mode, and the corrugation of the tip is the quantity which is most suitable to make contact with experiments. Here, we have calculated the bias range from −0.6 to +0.2 V with the tip height ~ 5.0 and 5.5 Å. In practice the tip height is hard to determine by direct way. Usually in the constant-current mode the average tip height corresponds to a certain tunnel-current and the negative bias corresponds to the occupied states on the surface in STM experiments. In Figures 3 and 4, a serial of typical corrugation topography for different sample bias, tip heights and absorbed sites were presented. In the two-dimensional (2D) images (left part of Figures 3 and 4), the black areas represent the low corrugation amplitude of tip and the white plots represent the high corrugation amplitude of tip. The right parts of Figures 3 and 4 are three-dimensional (3D) color surfaces with corrugation images. Actually the section of such 3D surface could be viewed as the line scan along certain path on the surface. The simulated STM line scans employed within Tersoff–Hamann approach show that the Pt (111) (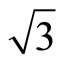 ×
×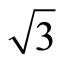 )R30˚/CO surface always yields the white corrugations on the CO atoms for fcc site adsorption with negative sample bias (see 2D images in Figure 3). Actually, it can be seen that in the same condition, the corrugation of CO in fcc site adsorption is lower than atop site. Meanwhile the STM images of the platinum layer in fcc adsorption are much rough than in atop’s. These obvious differences between fcc and atop adsorptions result from their different coordination numbers and perpendicular distances between carbon and platinum substrate (see Table IV, RC-S = 2.04 Å (atop), and 1.34 Å (fcc)). Therefore, the simulated STM images for CO on Pt (111) (
)R30˚/CO surface always yields the white corrugations on the CO atoms for fcc site adsorption with negative sample bias (see 2D images in Figure 3). Actually, it can be seen that in the same condition, the corrugation of CO in fcc site adsorption is lower than atop site. Meanwhile the STM images of the platinum layer in fcc adsorption are much rough than in atop’s. These obvious differences between fcc and atop adsorptions result from their different coordination numbers and perpendicular distances between carbon and platinum substrate (see Table IV, RC-S = 2.04 Å (atop), and 1.34 Å (fcc)). Therefore, the simulated STM images for CO on Pt (111) (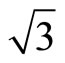 ×
×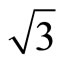 )R30˚ surface are in good agreement with the structural calculations in our work. Finally, it is noticed that the STM images calculated with 5.0 Å tip height are clearer than 5.5 Å. We hope that these images could be as distinct pictures to show the simulated STM line scans and to make comparisons with experiments.
)R30˚ surface are in good agreement with the structural calculations in our work. Finally, it is noticed that the STM images calculated with 5.0 Å tip height are clearer than 5.5 Å. We hope that these images could be as distinct pictures to show the simulated STM line scans and to make comparisons with experiments.
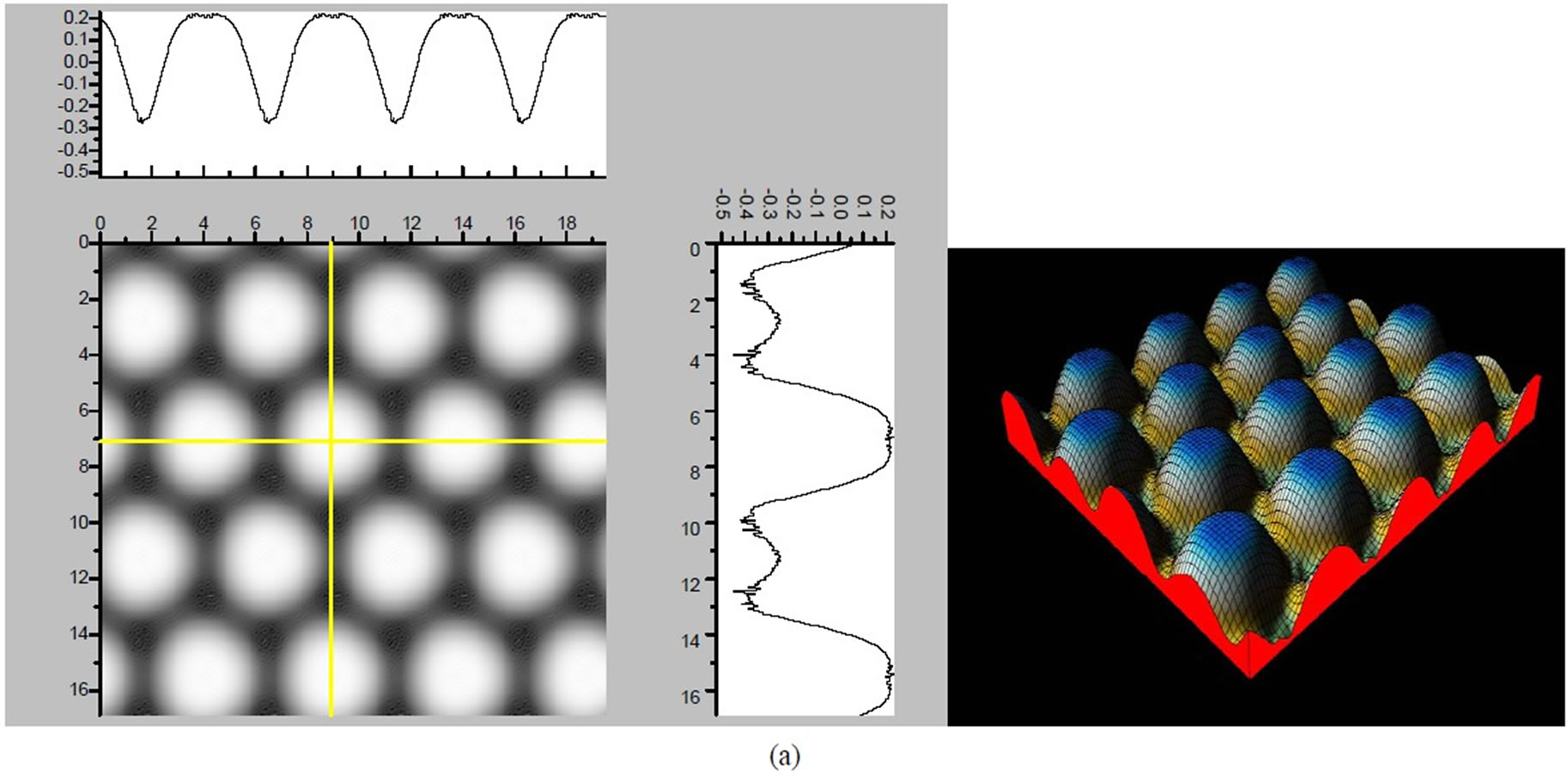
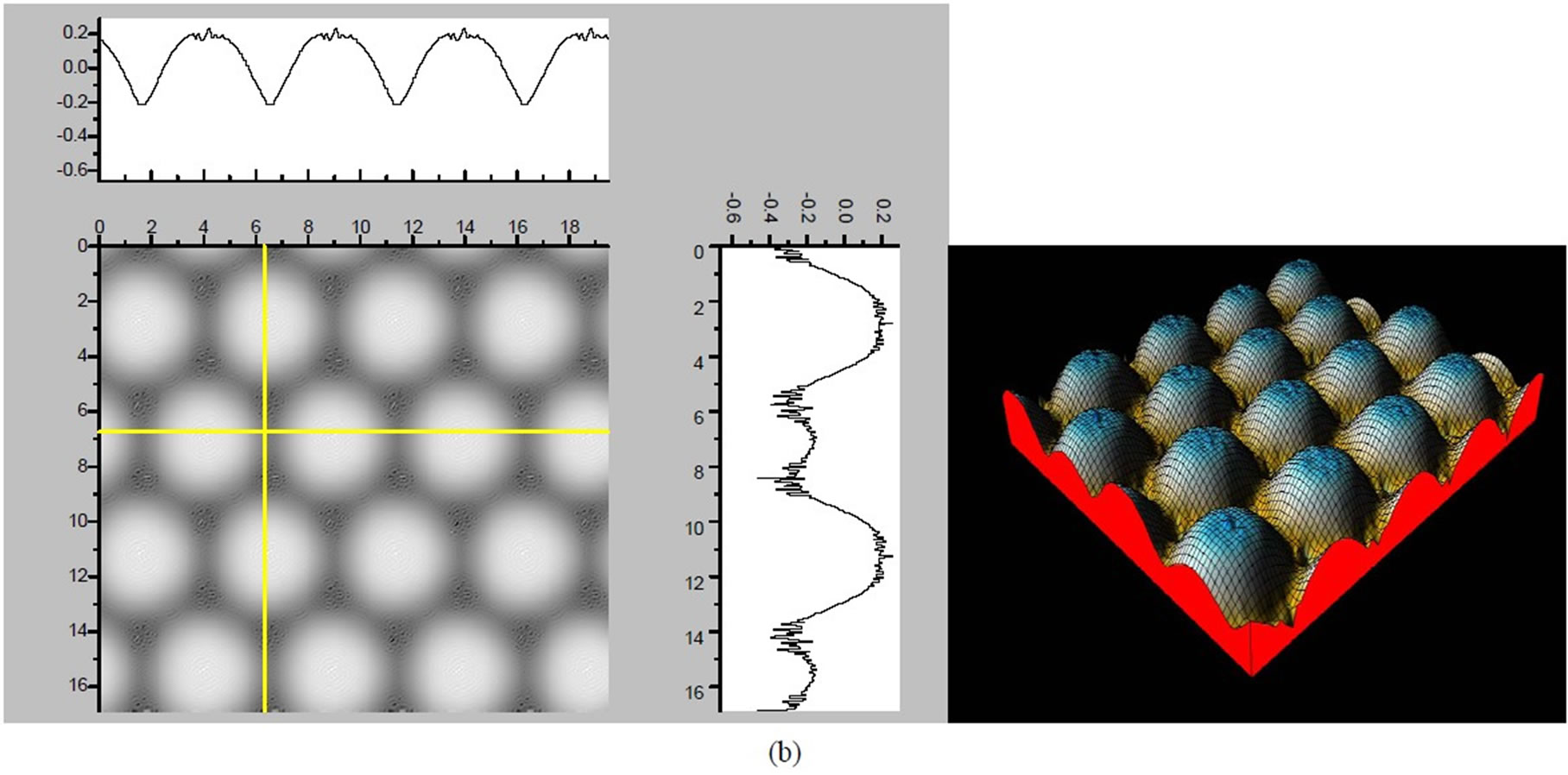
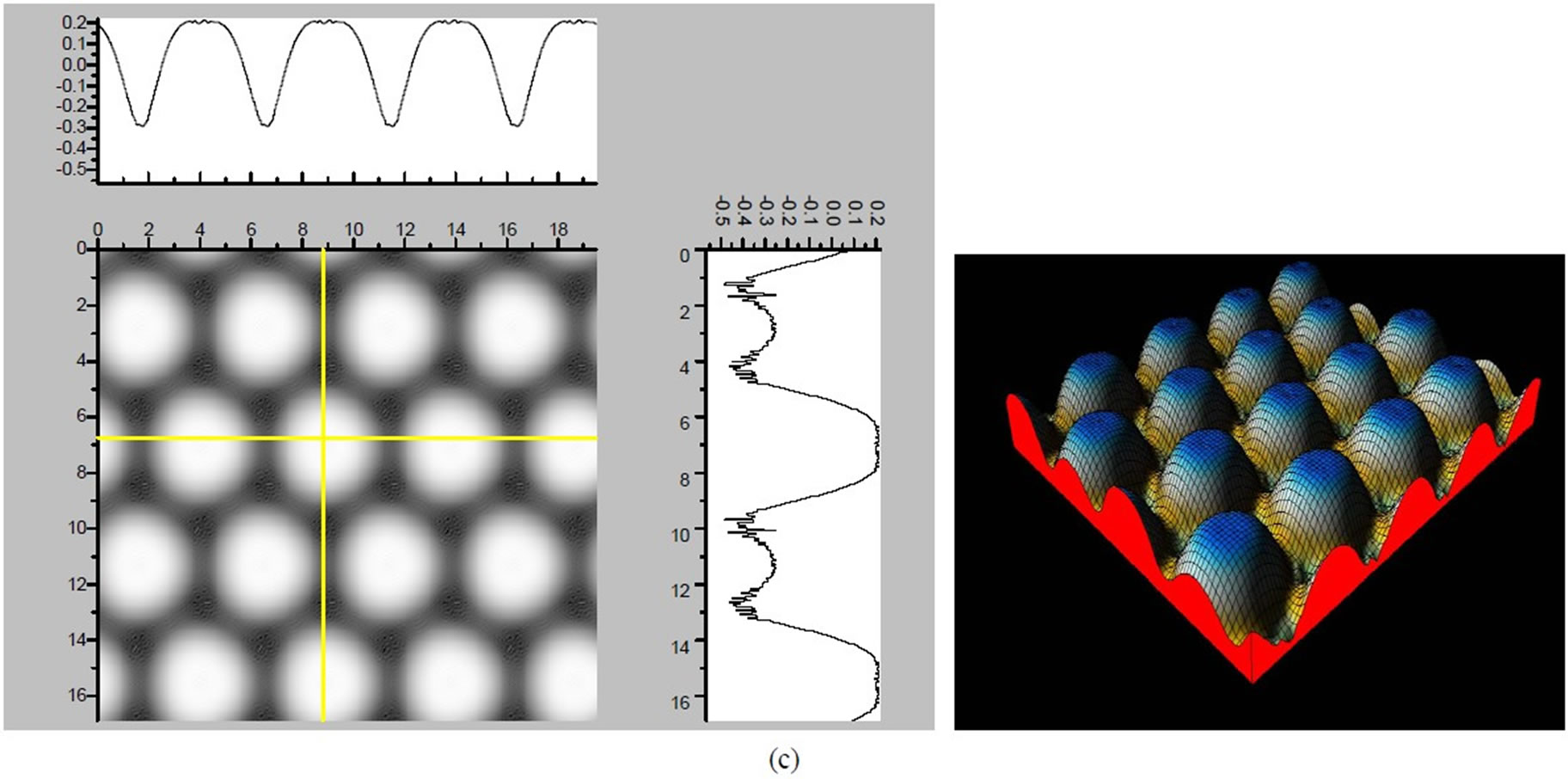

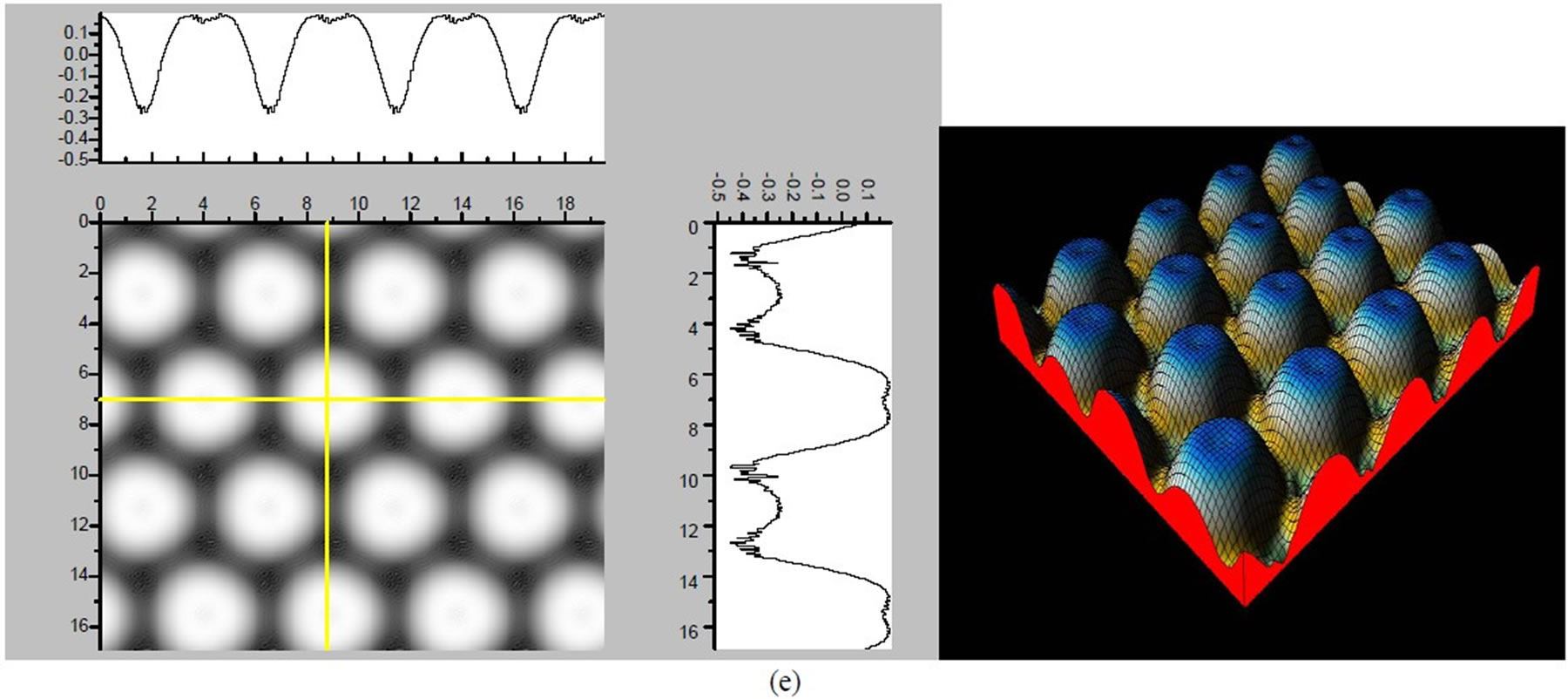
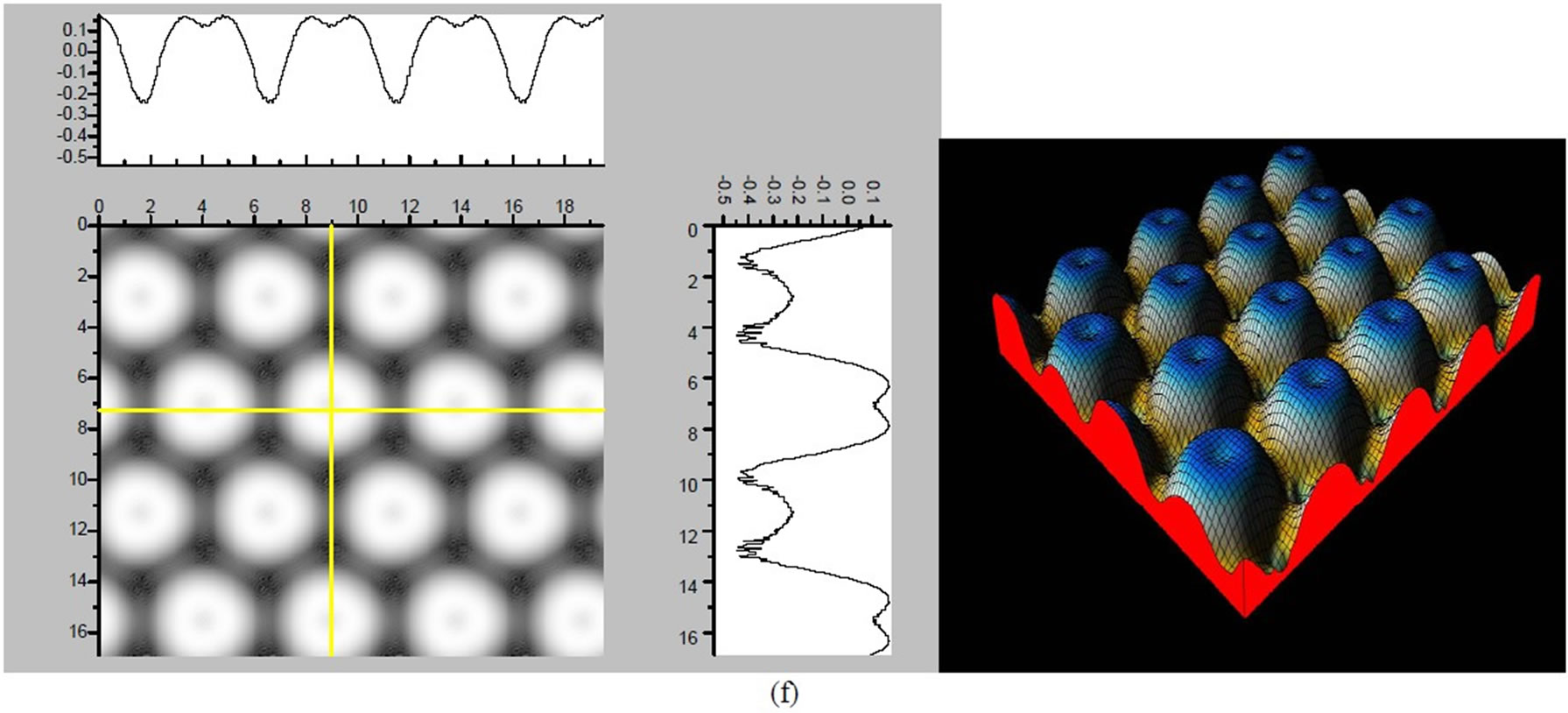
Figure 3. The simulated STM corrugation topography images of the Pt (111) ( ×
× )R30˚/CO surface with bias of −0.1, 0.2 V and tip heights of 5.0 Å and 5.5 Å. For each setting we provide here with the 3d color map and origin image, respectively. In the 3d map the vertical axis is the corrugation amplitude of STM tip in Å. In these simulated STM images the adsorbed CO molecule occupies fcc sites. (a) Vbias = −0.1 V tip height 5.0 Å; (b) Vbias = −0.1 V tip height 5.5 Å; (c) Vbias = −0.2 V tip height 5.0 Å; (d) Vbias = −0.3 V tip height 5.0 Å; (e) Vbias = −0.6 V tip height 5.0 Å; (f) Vbias = 0.2 V tip height 5.0 Å.
)R30˚/CO surface with bias of −0.1, 0.2 V and tip heights of 5.0 Å and 5.5 Å. For each setting we provide here with the 3d color map and origin image, respectively. In the 3d map the vertical axis is the corrugation amplitude of STM tip in Å. In these simulated STM images the adsorbed CO molecule occupies fcc sites. (a) Vbias = −0.1 V tip height 5.0 Å; (b) Vbias = −0.1 V tip height 5.5 Å; (c) Vbias = −0.2 V tip height 5.0 Å; (d) Vbias = −0.3 V tip height 5.0 Å; (e) Vbias = −0.6 V tip height 5.0 Å; (f) Vbias = 0.2 V tip height 5.0 Å.


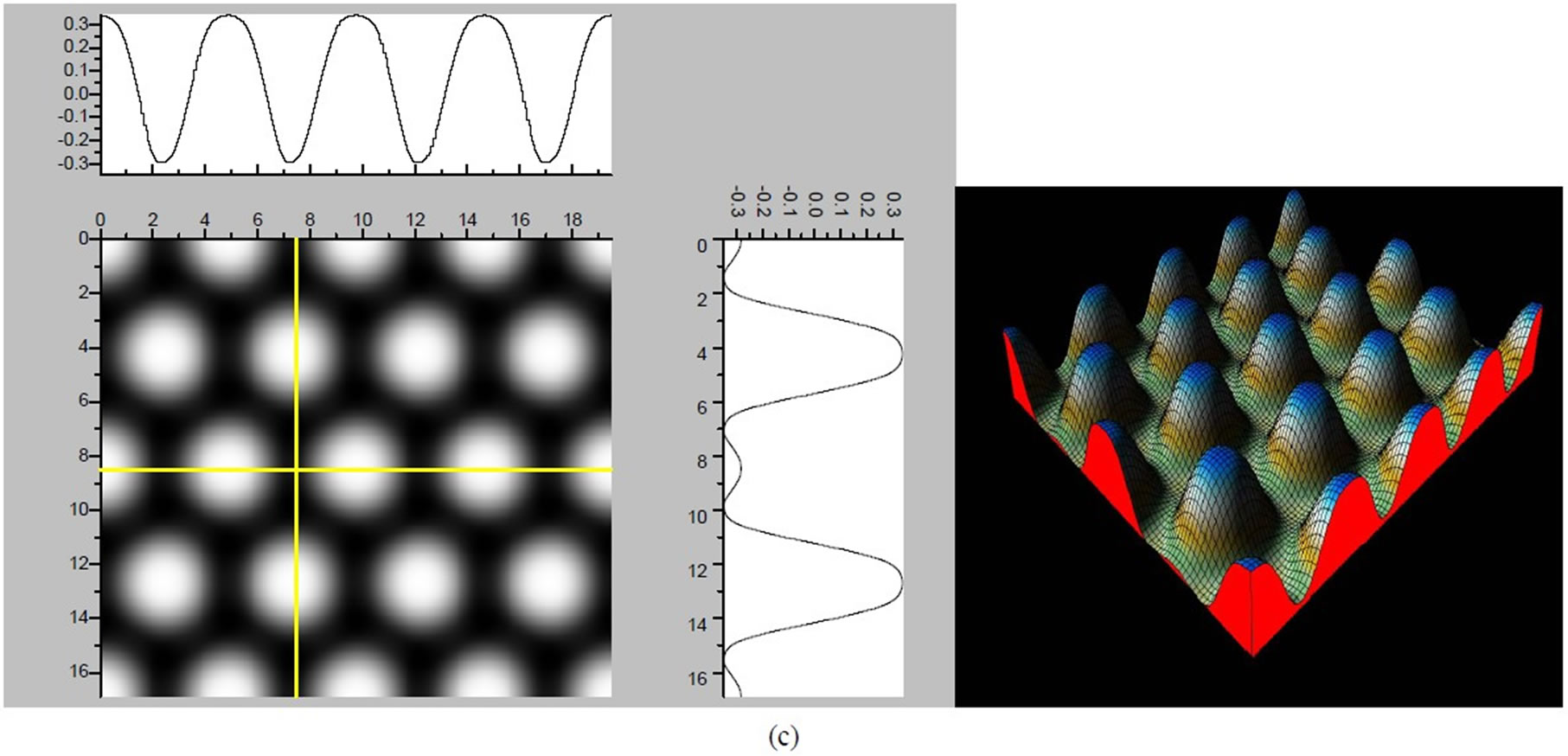
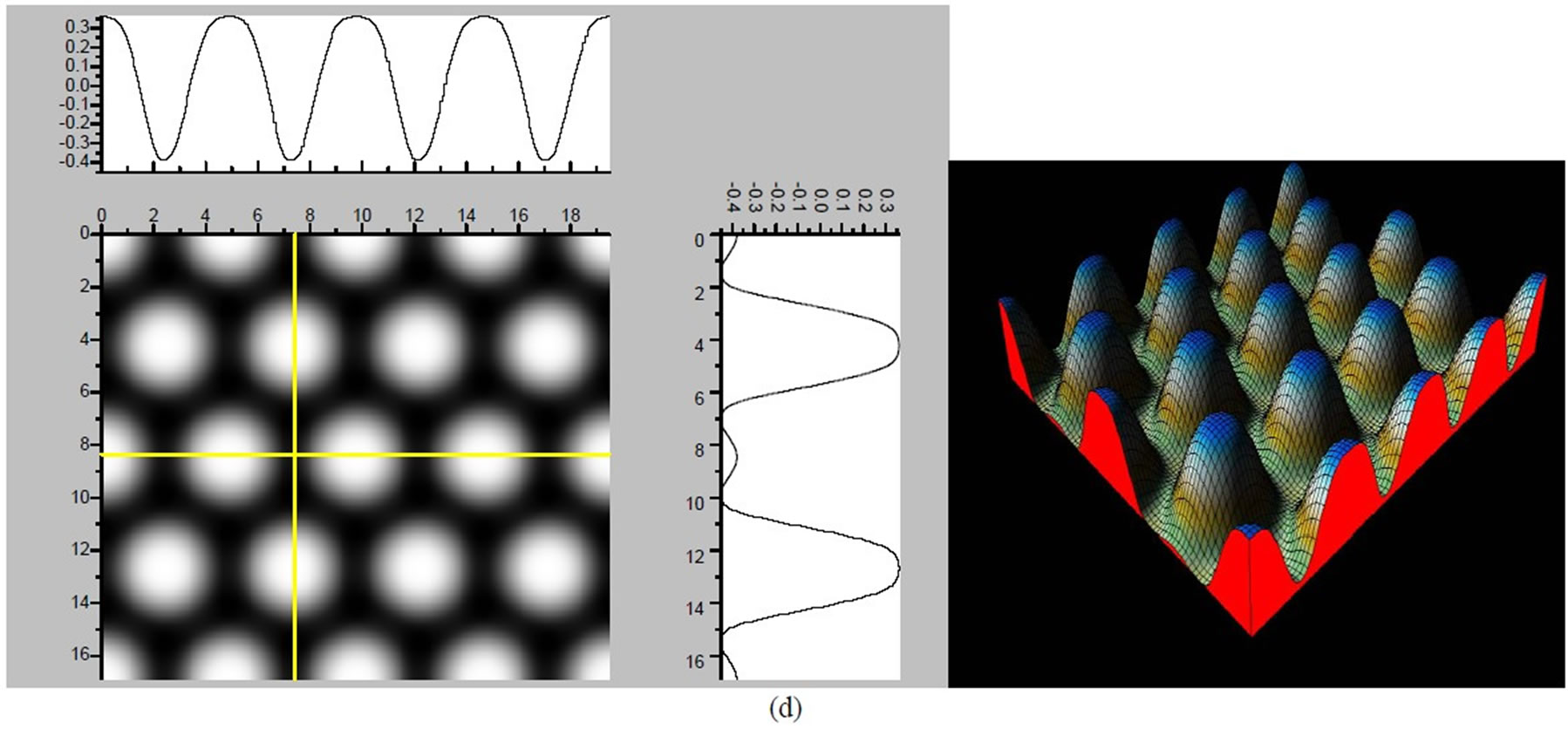
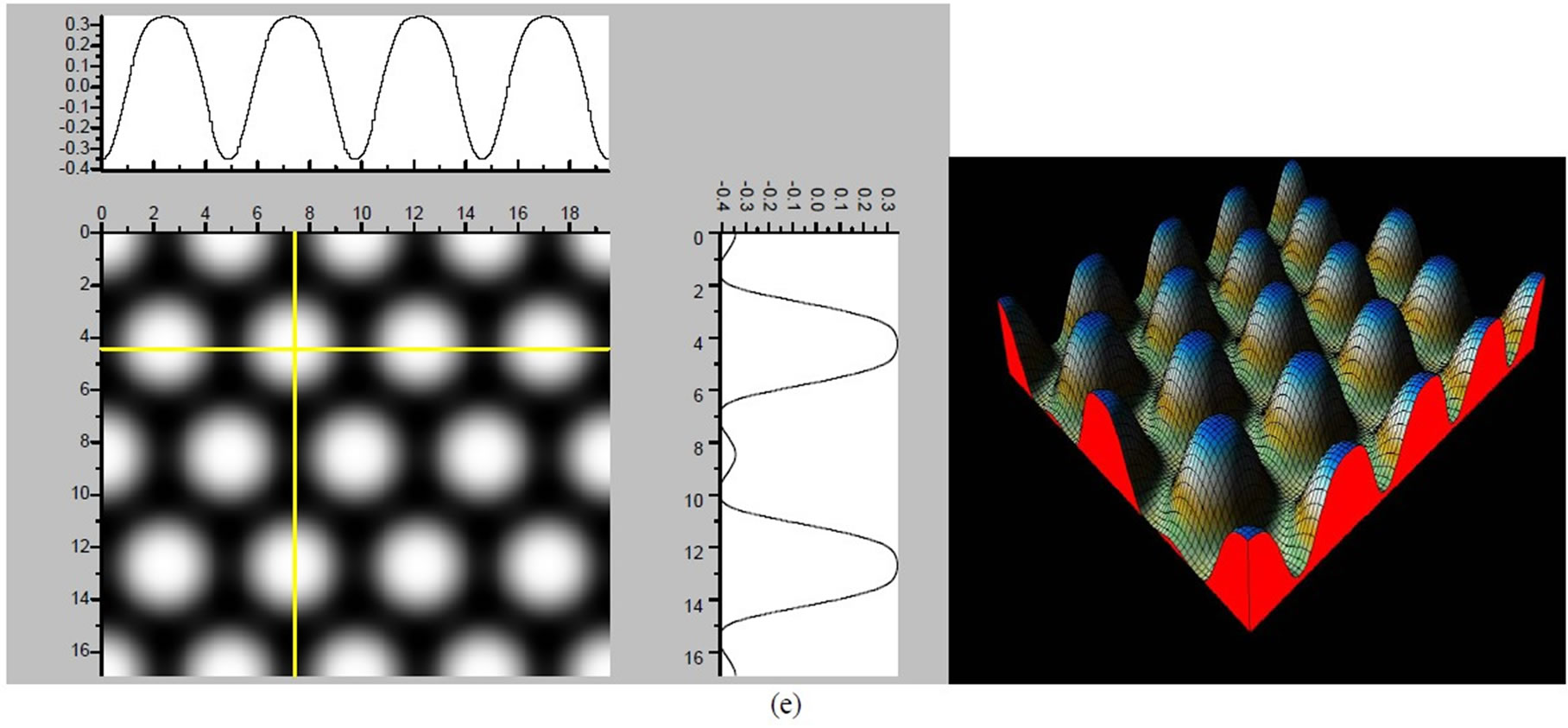
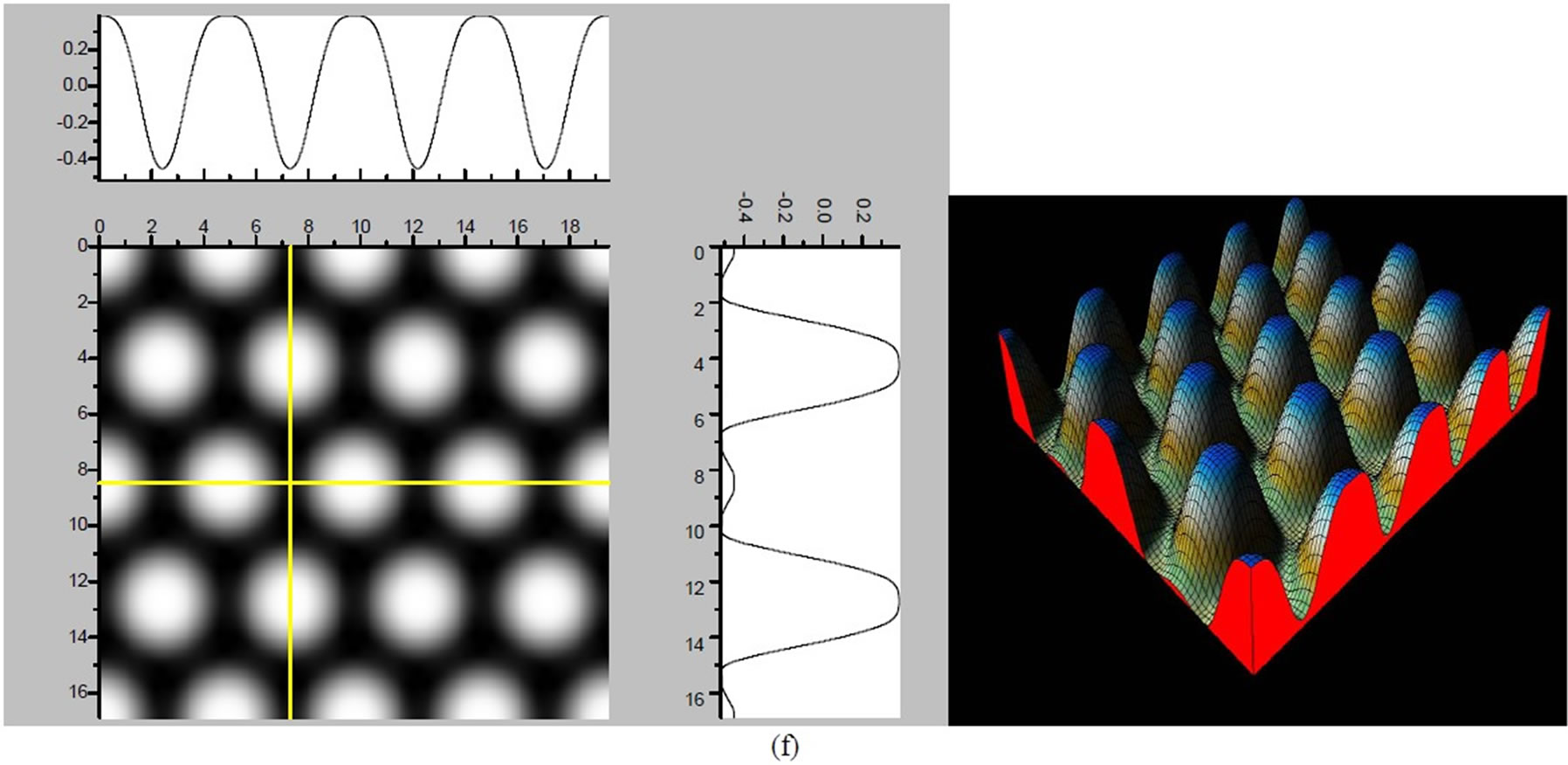
Figure 4. The simulated STM images of CO adsorption on atop sites. (a) Vbias = −0.1 V tip height 5.0 Å; (b) Vbias = −0.1 V tip height 5.5 Å; (c) Vbias = −0.2 V tip height 5.0 Å; (d) Vbias = −0.3 V tip height 5.0 Å; (e) Vbias = −0.6 V tip height 5.0 Å; Vbias = 0.2 V tip height 5.0 Å.
4. Summary and Discussion
In this article the atomic adsorption of CO on the Pt (111) (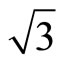 ×
× )R30˚ surface have been investigated by the first-principles total-energy calculations. The present work has resolved the argument on the CO adsorption position from different experimental and theoretical studies. The total-energy calculations showed that the average adsorption energy per CO molecule of Pt (111) (
)R30˚ surface have been investigated by the first-principles total-energy calculations. The present work has resolved the argument on the CO adsorption position from different experimental and theoretical studies. The total-energy calculations showed that the average adsorption energy per CO molecule of Pt (111) (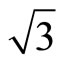 ×
×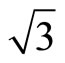 )R30˚/CO are ~1.54, 1.64, 1.66 eV in atop, hcp, and fcc sites, respectively, with little difference among various adsorption sites. Whereas there was a large difference (~1.2 eV) between the surface workfunctions of hollow (fcc and hcp) and atop adsorptions (see Table 3). It is worthy to point out that our calculated workfunction for atop site (~5.68 eV) is in good agreement with the experimental value (~5.70 eV). Comparison with previous theoretical calculations using different XC-functions, it is suggested that the total-energy calculations couldn’t confirm the perfect adsorption site absolutely. While, the results discussed by total-energy calculations and surface workfunctions are more scientific and reasonable. Thus, we supported that the atop adsorption is the perfect adsorption for Pt (111) (
)R30˚/CO are ~1.54, 1.64, 1.66 eV in atop, hcp, and fcc sites, respectively, with little difference among various adsorption sites. Whereas there was a large difference (~1.2 eV) between the surface workfunctions of hollow (fcc and hcp) and atop adsorptions (see Table 3). It is worthy to point out that our calculated workfunction for atop site (~5.68 eV) is in good agreement with the experimental value (~5.70 eV). Comparison with previous theoretical calculations using different XC-functions, it is suggested that the total-energy calculations couldn’t confirm the perfect adsorption site absolutely. While, the results discussed by total-energy calculations and surface workfunctions are more scientific and reasonable. Thus, we supported that the atop adsorption is the perfect adsorption for Pt (111) (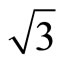 ×
× ) R30˚/CO system. In addition, the simulated STM line scans for the Pt (111) (
) R30˚/CO system. In addition, the simulated STM line scans for the Pt (111) (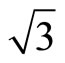 ×
× )R30˚/CO surface with fcc and atop adsorption have been calculated and shown. We hope that the simulated STM images are useful for providing information to further theoretical and experimental researches for Pt (111)/CO surface.
)R30˚/CO surface with fcc and atop adsorption have been calculated and shown. We hope that the simulated STM images are useful for providing information to further theoretical and experimental researches for Pt (111)/CO surface.
REFERENCES
- E. Frantzeskakis, S. Pons, A. Crepaldi, H. Brune, K. Kern, and M. Grioni, “Ag-Coverage-Dependent Symmetry of the Electronic States of the Pt (111)-Ag-Bi Interface: The ARPES View of a Structural Transition,” Physical Review B, Vol. 84, No. 24, 2011, Article ID: 245443. doi:10.1103/PhysRevB.81.241416
- J.-H. Fischer-Wolfarth, J. A. Farmer, J. M. FloresCamacho, A. Genest, I. V. Yudanov, N. Rösch, C. T. Campbell, S. Schauermann and H.-J. Freund, “ParticleSize Dependent Heats of Adsorption of CO on Supported Pd Nanoparticles as Measured with a Single-Crystal Microcalorimeter,” Physical Review B, Vol. 81, No. 24, 2010, Article ID: 241416. doi:10.1103/PhysRevB.84.245443
- R. Chen, Z. Chen, B. Mac, X. Hao, N. Kapur, J. Hyun, K. Cho and B. Shan, “CO Adsorption on Pt (111) and Pd (111) Surfaces: A First-Principles Based Lattice Gas MonteCarlo Study,” Computational and Theoretical Chemistry, Vol. 987, 2012, pp. 77-83. doi:10.1016/j.comptc.2011.07.015
- J. Steckel, A. Eichler and J. Hafner, “CO Adsorption on the CO-Precovered Pt (111) Surface Characterized by Density-Functional Theory,” Physical Review B, Vol. 68, No. 8, 2003, Article ID: 085416. doi:10.1103/PhysRevB.68.085416
- F. M. Leibsle, S. S. Dhesi, S. D. Barrett and A. W. Robinson, “STM Observations of Cu (100)-c (2 × 2) N Surfaces: Evidence for Attractive Interactions and an Incommensurate c (2 × 2) Structure,” Surface Science, Vol. 317, No. 3, 1994, pp. 309-320. doi:10.1016/0039-6028(94)90287-9
- T. M. Parker, L. K. Wilson, N. G. Condon and F. M. Leibsle, “Epitaxy Controlled by Self-Assembled Nanometer-Scale Structures,” Physical Review B, Vol. 56, No. 11, 1997, pp. 6458-6461. doi:10.1103/PhysRevB.56.6458
- H. Steininger, S. Lehwald and H. Ibach, “On the Adsorption of CO on Pt (111),” Surface Science, Vol. 123, No. 2-3, 1982, pp. 264-282. doi:10.1016/0039-6028(82)90328-4
- J. P. Biberian and M. A. Van Hove, “A New Model for CO Ordering at High Coverages on Low Index Metal Surfaces: A Correlation between LEED, HREELS and IRS: II. CO Adsorbed on fcc (111) and hep (0001) Surfaces,” Surface Science, Vol. 138, No. 2-3, 1984, pp. 361- 389. doi:10.1016/0039-6028(84)90253-X
- H. Hopster and H. Ibach, “Adsorption of CO on Pt (111) and Pt 6(111) × (111) Studied by High Resolution Electron Energy Loss Spectroscopy and Thermal Desorption Spectroscopy,” Surface Science, Vol. 77, No. 1, 1978, pp. 109-117. doi:10.1016/0039-6028(78)90164-4
- G. S. Blackman, M. L. Xu, D. F. Ogletree, M. A. Van Hove and G. A. Somorjai, “Mix of Molecular Adsorption Sites Detected for Disordered CO on Pt (111) by Diffuse Low-Energy Electron Diffraction,” Physical Review Letters, Vol. 61, No. 20, 1988, pp. 2352-2355. doi:10.1103/PhysRevLett.61.2352
- B. E. Hayden and A. M. Bradshaw, “The Adsorption of CO on Pt (111) Studied by Infrared Reflection-Absortion Spectroscopy,” Surface Science, Vol. 125, No. 3, 1983, pp. 787-802. doi:10.1016/S0039-6028(83)80060-0
- F. A. Pedersen and M. P. Andersson, “CO Adsorption Energies on Metals with Correction for High Coordination Adsorption Sites: A Density Functional Study,” Surface Science, Vol. 601, No. 7, 2007, pp. 1747-1753. doi:10.1016/j.susc.2007.01.052
- K. Doll, “CO Adsorption on the Pt (111) Surface: A Comparison of a Gradient Corrected Functional and a Hybrid Functional,” Surface Science, Vol. 573, No. 3, 2004, pp. 464-473. doi:10.1016/j.susc.2004.10.015
- P. E. Blöchl, “Projector Augmented-Wave Method,” Physical Review B, Vol. 50, No. 24, 1994, pp. 17953-17979. doi:10.1103/PhysRevB.50.17953
- J. P. Perdew, K. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996, pp. 3865-3868. doi:10.1103/PhysRevLett.77.3865
- J. P. Perdew, K. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 78, No. 7, 1997, pp. 1396-1396. doi:10.1103/PhysRevLett.78.1396
- G. Kresse and J. Furthermüller, “Efficiency of ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set,” Computational Materials Science, Vol. 6, No. 1, 1996, pp. 15-50. doi:10.1016/0927-0256(96)00008-0
- G. Kresse and J. Joubert, “From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method,” Physical Review B, Vol. 59, No. 3, 1999, pp. 1758-1775.
- doi:10.1103/PhysRevB.59.1758
- D. Vanderbilt, “Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism,” Physical Review B, Vol. 41, No. 11, 1994, pp. 7892-7895. doi:10.1103/PhysRevB.41.7892
- T. Charpentier, “The PAW/GIPAW Approach for Computing NMR Parameters: A New Dimension Added to NMR Study of Solids,” Solid State Nuclear Magnetic Resonance, Vol. 40, No. 1, 2011, pp. 1-20. doi:10.1016/j.ssnmr.2011.04.006
- H. J. Monkhorst and J. D. Pack, “Special Points for Brillouin-Zone Integrations,” Physical Review B, Vol. 13, No. 12, 1976, pp. 5188-5192. doi:10.1103/PhysRevB.13.5188
- E. Frantzeskakis, S. Pons, A. Crepaldi, H. Brune, K. Kern and M. Grioni, “Ag-Coverage-Dependent Symmetry of the Electronic States of the Pt (111)-Ag-Bi Interface: The ARPES View of a Structural Transition,” Physical Review B, Vol. 84, No. 24, 2011, Article ID: 245443. doi:10.1103/PhysRevB.84.245443
- M. C. Payne, M. O. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, “Iterative Minimization Techniques for ab Initio Total-Energy Calculations: Molecular Dynamics and Conjugate Gradients,” Reviews of Modern Physics, Vol. 64, No. 4, 1192, pp. 1045-1097. doi:10.1103/RevModPhys.64.1045
- C. Kittel, “Introduction to Solid State Physics,” 5th Edition, John Wiley & Sons, Inc., New York, 1976, p. 31.
- D. L. Adams, H. B. Nielsen and M. A. Van Hove, “Quantitative Analysis of Low-Energy-Electron Diffraction: Application to Pt (111),” Physical Review B, Vol. 20, No. 12, 1979, pp. 4789-4806. doi:10.1103/PhysRevB.20.4789
- N. Materer, U. Starke, A. Barbieri, R. Döll, K. Heinz, M. A. van Hove and G. A. Somorjai, “Reliability of Detailed LEED Structural Analyses: Pt (111) and Pt (111)-p (2 × 2)-O,” Surface Science, Vol. 325, No. 3, 1995, pp. 207- 222. doi:10.1016/0039-6028(94)00703-9
- R. Feder, H. Pleyer, P. Baner and N. Mueller, “Spin Polarization in Low-Energy Electron Diffraction: Surface Analysis of Pt (111),” Surface Science, Vol. 109, No. 2, 1981, pp. 419-434. doi:10.1016/0039-6028(81)90497-0
- K. Hayek, H. Glassl, A. Gutmann and H. Lenohard, “A LEED Analysis of the Structure of Pt (111) (
 ×
×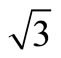 ) R30˚-S,” Surface Science, Vol. 152-153, No. 1, 1985, pp. 419-425. doi:10.1016/0039-6028(85)90172-4
) R30˚-S,” Surface Science, Vol. 152-153, No. 1, 1985, pp. 419-425. doi:10.1016/0039-6028(85)90172-4 - Ž. Crljen, P. Lazić, D. Šokčevic´ and R. Brako, “Relaxation and Reconstruction on (111) Surfaces of Au, Pt, and Cu,” Physical Review B, Vol. 68, No. 19, 2003, Article ID: 195411. doi:10.1103/PhysRevB.68.195411
- X.-M. Tao, M.-Q. Tan, X.-X. Zhao, W.-B. Chen, X. Chen and X.-F. Shang, “A Density-Functional Study on the Atomic Geometry and Adsorption of the Cu (100) c (2 × 2)/N Surface,” Surface Science, Vol. 600, No. 17, 2006, pp. 3419-3426. doi:10.1016/j.susc.2006.06.032
- M. Methfessel, D. Hennig and M. Scheffler, “Trends of the Surface Relaxations, Surface Energies, and Work Functions of the 4d Transition Metals,” Physical Review B, Vol. 46, No. 8, 1991, pp. 4816-4829. doi:10.1103/PhysRevB.46.4816
- A. D. Becke, “Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior,” Physical Review A, Vol. 38, No. 6, 1988, pp. 3098-3100. doi:10.1103/PhysRevA.38.3098
- J. Kohanoff, “Electronic Structure Calculations for Solids and Molecules: Theory and Computational Methods,” Cambridge University Press, Cambridge, 2006, pp. 77-84. doi:10.1017/CBO9780511755613
- R. Colle and D. Salvetti, “Approximate Calculation of the Correlation Energy for the Closed Shells,” Theorefica Chimica Acta, Vol. 37, No. 4, 1975, pp. 329-334. doi:10.1007/BF01028401
- D. R. Lide, “CRC Handbook of Chemistry and Physics,” 84th Edition, CRC Press, Boca Raton, 2003-2004, pp. 12- 124.
- A. Gil, A. Clotet, J. M. Ricart, G. Kresse, M. García-Hernández, N. Rösch and P. Sautet, “Site Preference of CO Chemisorbed on Pt (111) from Density Functional Calculations,” Surface Science, Vol. 530, No. 1-2, 2003, pp. 71-87. doi:10.1016/S0039-6028(03)00307-8
- S. A. Wasileski, M. J. Weaver and M. T. M. Koper, “Potential-Dependent Chemisorption of Carbon Monoxide on Platinum Electrodes: New Insight from Quantum-Chemical Calculations Combined with Vibrational Spectroscopy,” Journal of Electroanalytical Chemistry, Vol. 500, No. 1-2, 2001, pp. 344-355. doi:10.1016/S0022-0728(00)00420-4
- F. Illas, F. Mele, D. Curulla, A. Clotet and J. M. Ricart, “Electric Field Effects on the Vibrational Frequency and Bonding Mechanism of CO on Pt (111),” Electrochimica Acta, Vol. 44, No. 6-7, 1998, pp. 1213-1279. doi:10.1016/S0013-4686(98)00224-2
- C. Klünker, M. Balden, S. Lehwald and W. Daum, “CO Stretching Vibrations on Pt (111) and Pt(110) Studied by Sumfrequency Generation,” Surface Science, Vol. 360, No. 1-3, 1996, pp. 104-111. doi:10.1016/0039-6028(96)00638-3
- M. O. Pedersen, M. L. Bocquet, P. Sautet, E. Laegsgaard, I. Stensgaard and F. Besenbacher, “CO on Pt (111): Binding Site Assignment from the Interplay between Measured and Calculated STM Images,” Chemical Physics Letters, Vol. 299, No. 5, 1999, pp. 403-409. doi:10.1016/S0009-2614(98)01318-9
- W. Liu, Y. F. Zhu, J. S. Lian and Q. Jiang, “Adsorption of CO on Surfaces of 4d and 5d Elements in Group VIII,” The Journal of Physical Chemistry C, Vol. 111, No. 2, 2007, pp. 1005-1009. doi:10.1021/jp0661488
- J. Tersoff and D. R. Hamann, “Theory and Application for the Scanning Tunneling Microscope,” Physical Review Letters, Vol. 50, No. 25, 1983, pp. 1998-2001. doi:10.1103/PhysRevLett.50.1998

