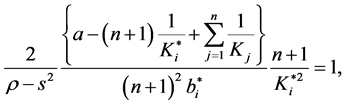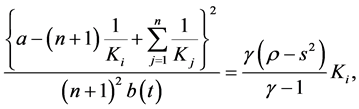Received 6 December 2015; accepted 14 January 2016; published 19 January 2016

ABSTRACT

By making use of the optimal stopping theory, we construct a multi-stage stochastic Cournot model to examine the effect of increase in uncertainty and number of entrants on the amount and timing of strategic cost reduction investment. It is revealed that firms should enlarge and postpone the investment if 1) the market is more uncertain, or 2) there exist more firms in the market.

Keywords:

Cournot Competition, Optimal Stopping Theory, Geometric Brownian Motion, Cost Reduction Investment, Value of Waiting

1. Introduction

Studies on oligopolistic markets under uncertainty, which progressed by paying attention to information sharing with rivals (Basar and Ho (1974) [1] , Ponssard (1979) [2] , Novshek and Sonnenschein (1982) [3] , Gal-Or (1986) [4] , etc.), have entered a new stage since Youn and Tremblay (2015) [5] introduced Brownian motion into the modelling of quantity competition. By formulating management errors with Brownian motion, Youn and Tremblay (2015) [5] predicted that firm’s failure was more likely in smaller markets and for firms that were smaller and less efficient at managing errors. As earlier studies that utilized stochastic motions for formulation of quantity competition, Fujita (2007) [6] revealed the consequences of interaction of exporting firms and Fujita (2008) [7] demonstrated another economic channel for the excess entry theorem, by combining market equilibrium theory with optimal stopping theory, which had been used to develop strategies on timing in a stochastically fluctuating economy since McDonald and Siegel (1986) [8] demonstrated the “value of waiting”. As other studies of this field, Dixit (1989) [9] examined the timing of entering foreign market, while Farzin, Huisman and Kort (1988) [10] investigated the timing of IT investment. Bentolila and Bertola (1990) [11] , on the other hand, considered the timing of employment/lay-off.

The present paper attempts to push forward these studies by focusing on Cournot competition in a stochastically fluctuating market. More precisely, we construct a multi-stage stochastic Cournot model based on the optimal stopping theory to examine the effect of increase in uncertainty and number of entrants on the amount and timing of the strategic cost reduction investment.

Structure of this paper is as follows. Section 2 lays out a stochastic dynamic Cournot model and derives the conditions for the optimal amounts of the output and the investment. Section 3 derives the condition for the optimal timing of the investment. Based on these analyses, Section 4 reveals the effect of increase in uncertainty and number of entrants on the optimal amount and timing of the investment. Concluding remarks are made in Section 5.

It is revealed that firms should enlarge and postpone the investment if 1) the market is more uncertain, or 2) there exist more firms in the market.

2. Basic Model

Let us consider a stochastic oligopolistic market where time passes continuously with importance of the future diminishing with discount rate ρ. There exist n identical firms that are planning to enter the market to produce homogeneous goods in a Cournot fashion, engaging in two stage game, i.e., each firm determines amount and timing of investment in the first stage, and then, in the second stage, amount of output in each period after the investment. Let us assume that the ith firm’s investment K_i reduces its marginal cost c_i, which we assume to be constant over time once the investment was conducted. In the following, in order to simplify the analysis, we

specify the relationship between the ith firm’s marginal cost and investment as.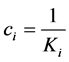

Letting x_i(t) and p(t) denote the ith firm’s output and the unit price in period t, respectively, we assume p(t) is related to the total output in period t, 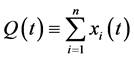, through the following inverse demand function

,

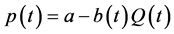where a is a positive constant that expresses the choke price, while b is a positive variable that expresses the size of the market, which we assume to fluctuate stochastically according as the following geometric Brownian motion:

(1)

with initial value b₀, where s is a positive constant that expresses volatility in a sense that larger s means more uncertain expansion of the market, while dz is Wiener process that expresses the random movement.

Following the standard procedure of the backward induction, to begin with, let us determine the optimal output of each firm in the second stage. Since the ith firm’s profit in period t after the investment, π_i(t), is described as

,

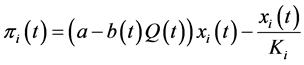we have the ith firm’s output and profit in the Cournot equilibrium in period t, respectively, as

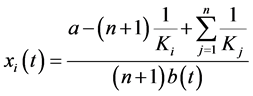; (2)

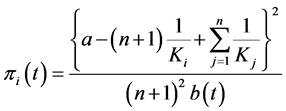, (3)

from the ith firm’s first order condition for profit maximization 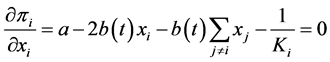for every.

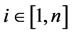Since we have the following equations from Equation (3)

;

,

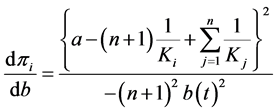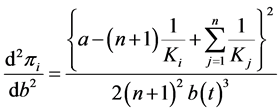we can express the stochastic process of the ith firm’s profit, by making use of Ito’s lemma, as

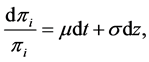(4)

with initial value π₀, where μ = s² and σ = −s.

If we let 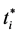and 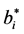denote the period when the ith firm carries out the investments and the b in period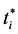, respectively, sum of the net present value of the profit in each period after the investment, evaluated at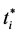, is

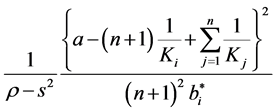
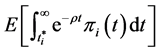
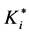
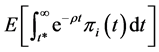
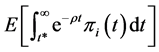
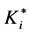
obtained as by calculating. Since the ith firm determines the optimal amount of the investment to maximize minus the investment K_i, the optimal amount of the investment is determined to equalize the marginal values of and K_i. Thus, we have the condition must satisfy as

which reduces to

, (5)

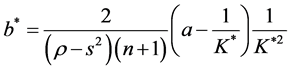
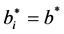
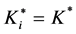
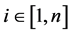
by assuming symmetric solution, i.e., and for every, and rearranging the terms.

3. Condition for the Optimal Timing of the Investment

In this section, we derive the condition for the ith firm’s optimal timing of the investment in the first stage.

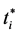
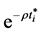
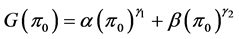
As a preliminary, let us derive the expected value of one unit of profit at (i.e., the expected value of). For this purpose, if we let G(π₀) denote this value, the general solution to G(π₀) is expressed as

, (6)

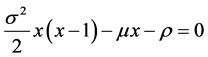
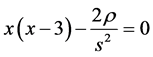
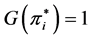
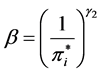
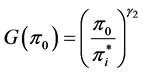
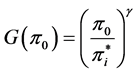
where γ₁ < 0 and γ₂ > 0 are solutions to the characteristic equation, which is rewritten as by substituting μ = s² and σ = −s into it. Since G(π₀) satisfies G(∞) = 0 and, it follows that α = 0 and, which combined with Equation (6) yields. Letting γ denote γ₂, we obtain

, (7)

where

. (8)

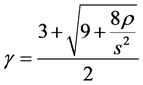
Thus, we can express the ith firm’s object function V_i to maximize in period 0 as

. (9)

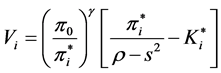
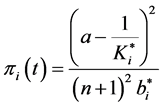
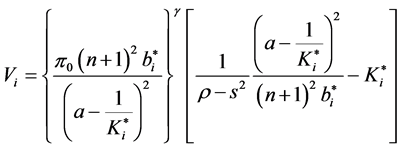
By substituting the ith firm’s profit in the symmetric equilibrium into Equation (9), we have

, (10)

from whose derivative with respect to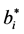, the following first order condition is obtained.

which reduces to

, (11)

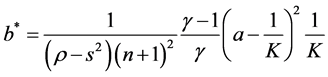
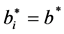
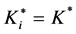
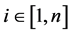
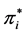
by assuming symmetric solution, i.e., and for every, and rearranging the terms. Note that since the model of the present paper is stochastic, the optimal timing is expressed by cut off level of b. Note also that Equation (11) is equivalent to what is derived by differentiating V_i with respect to, setting it to zero and assuming the symmetric solution.

4. Optimal Amount and Timing of the Investment

Now we are ready to determine the optimal amount and timing of the investment. By solving Equation (5) (optimal condition for the amount of the investment) and Equation (11) (optimal condition for the timing of the in-

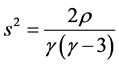
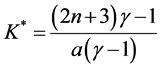
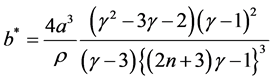
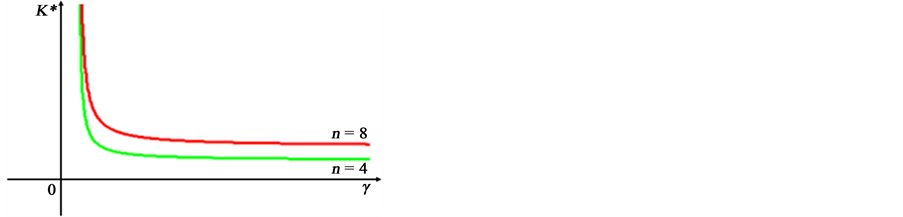
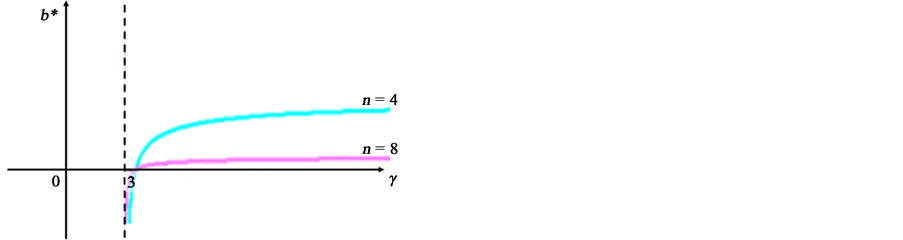
vestment) with respect to K and b, and making use of (which is obtained from Equation (8)), we have the optimal amount and timing of the investment as

; (12)

. (13)

If we assume for example that a = 10 and ρ = 1.2, graphs of Equation (12) and Equation (13) are depicted as in Figure 1 and Figure 2, respectively, for n = 4 and n = 8.

Since K^* is a decreasing function as in Figure 1 while b^* is an increasing function with respect to γ in a relevant range as in Figure 2, and it is clear from Equation (8) that increase in s reduces γ, we can see that increase

in s increases K^* and reduces b^*. Since we have 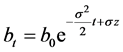from Equation (1), it follows that smaller b^* is

equivalent with postponement of the investment. Since we can also see from Equation (12) and Equation (13) that graph of K^* shifts upward while graph of b^* shifts downward in accordance with an increase in n as in Figure 1 and Figure 2, we have the following proposition.

Proposition: Firms should enlarge and postpone the investment if 1) the market is more uncertain, or 2) there exist more firms in the market.

5. Concluding Remarks

By constructing a theoretical model that combines Cournot competition with stochastic motion, the present paper attempts to examine the effect of an increase in uncertainty and number of entrants on the amount and timing of the strategic cost reduction investment.

It is revealed that firms should enlarge and postpone the investment if 1) the market is more uncertain, or 2) there exist more firms in the market. We can see that the investment should be enlarged if the value of waiting rises in accordance with increase in uncertainty and number of entrants.

It is necessary to examine the robustness of the results by assuming more general demand function and cost function. It is also necessary to relax the assumption of geometric Brownian motion, as well as to give an empirical testing of this model. We take up such analysis next, hoping to contribute to the advancement of the theory of the Cournot competition in a stochastically fluctuating market.

Acknowledgements

The author is grateful for the reviewers’ valuable comments that improved the manuscript.

Cite this paper

YasunoriFujita, (2016) Optimal Amount and Timing of Investment in a Stochastic Dynamic Cournot Competition. Theoretical Economics Letters,06,1-6. doi: 10.4236/tel.2016.61001

References