Received 4 August 2015; accepted 22 September 2015; published 28 September 2015

ABSTRACT

Existing classical theory cannot explain consumer behavior of cutting consumption into smaller bundles instead of consuming everything in one bundle. We present a model that separates consumer behavior into two steps. At first, the consumer decides on the amount of working hours, which defines his income. In the second step, s/he decides on the number of consumption bundles. Since a consumer has larger utility when cutting consumption into smaller bundles, while on the other hand s/he faces higher costs when buying smaller bundles, s/he can take both factors into consideration when deciding on the optimal number of consumption bundles.

Keywords:

Consumption, Bundles

1. Introduction

Classical labor theory assumes that consumption within a given time period is consumed in one chunk, however, in reality, people cut their consumption into smaller bundles.

There are many indirect costs associated with cutting consumption into smaller bundles, for example, the cost of driving to malls, shops, hotels, distant cities and countries when on vacation or simply when consuming products during leisure time.

Crafton (1979) [1] discussed the idea of cost associated with consumption in bundles. His main focus was firms’ optimal pricing of their goods, taking into consideration different parking costs, consumption time (waiting in lines) and travel time compared to these costs when consumers bought from competitors. Gwartney et al. (2003: p. 162) [2] wrote that one measure of the value of time was how much extra people would pay to save one hour on a nonstop plane flight. Ekelund and Tollison (1991: chap. 6) [3] also discussed the fact that many goods had a money cost and a time cost. Santerre and Neun (2000: p. 113) [4] described a study that investigated how much people were willing to pay to shorten the waiting time for a dentist. Eaton and Eaton (1988: chap. 4) [5] pointed out that the money price of a product that took time to consume was not the complete or full price. Rather, one must account for both the money cost and the money value of the time needed to consume each good.

We couldn’t find any literature regarding the cost of separating consumption into small segments. In this paper, we present a simple model that takes into consideration the effect of separating consumption into small chunks on consumer behavior.

2. The Model

Becker (1965) [6] incorporated time cost as a relevant variable in individual optimization problems. As in the classical model, let us assume that an agent’s utility function is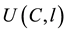, and that the agent is considering leisure and consumption during a month.

C is the amount of monthly consumption and l is the amount of monthly leisure consumed within a given time period.

We assume that when the agent utilizes a chunk of consumption, s/he must bear the cost of getting to a center (travel, taking care of children at home, parking costs, etc.), or getting to hotel, or another country during vacation, etc.

If an agent consumed everything in one chunk, the monthly budget constraint is:

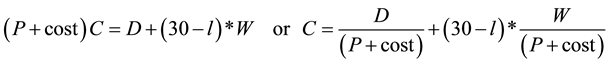(1)

For:

P: price of one unit of consumption;

Cost: the cost of consuming one chunk of consumption;

D: non-working income (interest, rent);

W: wage per day.

However, if the consumer consumes in n chunks, the monthly budget constraint is:

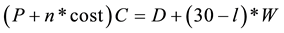, or:

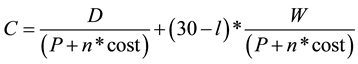(2)

It is easy to see that the agent suffers from a reduction in real wage per month as s/he consumes in smaller chunks.

As we can see in Figure 1 below, the agent will move to a lower budget constraint as n, the number of consumption chunks within a month is larger.

Due to the substitution effect, the agent will prefer to consume more leisure and reduce working hours, while due to the income effect s/he would decrease leisure and increase working hours. If the substitution effect dominates, s/he will move to a point such as B, while if the income effect dominates s/he would move to point such as C.

Whether s/he moves to point B or to point C, utility is reduced as the agent cuts consumption into smaller and smaller chunks.

There is no doubt that agents will prefer point A over points B or C, which means that agents would prefer to concentrate all consumption, including consumption during leisure, in one chunk. According to this, we would expect an agent to take a few concentrated days of vacation each month (or an even longer time span) as leisure time. This time will be dedicated to buying consumption goods, while during the rest of the month, s/he will concentrate working hours.

However, in reality, most agents tend to separate their leisure time into smaller chunks, as well as consuming in smaller chunks. They tend not to concentrate consumption in one chunk, contrary to what we would expect according to the classical approach.

2.1. A Model of Consuming in Smaller Bulks

We suppose that due to decreasing marginal utility from consumption, people will have higher utility when consuming a given amount of consumption in smaller bulks.

Let us define

C: total consumption within a given time period;

n: the number of chunks.

We assume that:

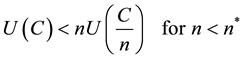, while.

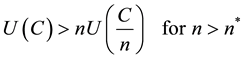The consumer will prefer to cut consumption into smaller bundles up to an optimal bundle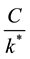. Cutting consumption beyond 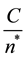will reduce utility.

Figure 2 presents the utility derived from consuming the amount C cut into various numbers of bundles.

The horizontal axe defines the size of consumption amount C cut into n bundles while the vertical axis defines the utility derived by the consumer when consuming l bundle of a size.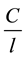

2.2. Indifferent Utility Bundles

When consuming an amount C, the consumer will have higher utility then when consuming the amount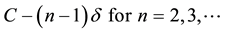. However, his utility from consuming n bundles, each of the size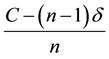, might

be higher than consuming one bundle at an amount C.

Due to decreasing marginal utility from consumption, consumers might get lower level of utility when consuming all their periodical consumption in one bundle or when giving up units of consumption while cutting their consumption to n different bundles.

Figure 3 presents bundle utility curves for various levels of aggregate consumption.

We should notice that

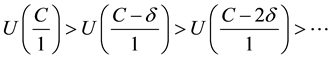(3)

Notice that consuming an amount 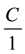in one bundle gives the same utility as consuming the amount 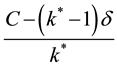in different bundles, although is larger than.

According to Figure 3, if the consumer is able to finance consumption at the amount which will be consumed in one bundle, s/he will consider cutting it into smaller bundles. Cutting it into 2 bundles, each at the amount, will bring a utility of (see point A) which is higher than. Cutting it into 3 bundles, each at the amount, will bring an even higher utility (see point B).

The optimal number of bundles is m if

(4)

2.3. Maximizing Utility

Given consumer income, s/he will try to maximize utility from consumption by cutting it into optimal number of bundles. However, when s/he cuts consumption to smaller bundles, s/he suffers a loss of income due to the indirect cost mentioned before.

For example, let assume that s/he can consume units of consumption in one bulk, however, when cutting

it into n smaller bulks, s/he suffers an indirect cost of units of consumption. Notice that according to the utility functions depicted in Figure 3, although he suffers the indirect cost of cutting consumption into smaller bundles, his utility can rise. For example, if s/he decides to buy 2 bundles of consumption, his total amount

of consumption is. However, his utility from buying 2 bundles, each the amount of is (point C), higher than. Then he considers buying 3 bundles of consumption, each at the amount, his utility is (point D). We can see that although he suffers a loss of consumption due to the indirect cost associated with increasing the number of bundles, his utility is higher.

2.4. Selection Process

We assume that the consumer has utility from leisure and consumption.

S/He makes 2 different choices, the first is how many hours to work (which determines leisure), which defines the amount of income s/he can get, and the second is into how many bundles to cut his consumption.

The consumer problem becomes:

(5)

Given the amount of leisure chosen, his working income is, s/he can decide the optimal number of bundles by solving:

(5')

2.5. Example

Let assume that the utility function when deciding on leisure and total consumption is and in the first step s/he solves:

(6)

We get:

(6')

Let assume that the utility function when deciding on the number of bundles is:

(7)

In the second step, s/he solves:

(8)

Given optimal l from first step and given D, P and cost, we calculate the optimal n by substituting constraint into utility function and differentiating subject to n:

(8')

Differentiating subject to n and equalizing to zero, we get the following equation:

. (9)

Dividing both sides by we get:

(9')

The equation cannot be solved analytically, but given T, W, D, P and cost, the number of bundles can be solved numerically.

As a numerical illustration, let assume:

We get

Substituting into (9') we get:

(9")

As we can see the consumer prefers to cut his consumption to small bundles, barring a cost of 17.5615 units of consumption rather than consuming a larger aggregated amount in smaller number of bundles.

Table 1 and Figure 4 show the connection between the number of bundles, n, and consumer utility according to Equation (8').

3. Summary

Classical consumption theory ignores the fact that most consumers do not regard consumption as one aggregated chunk, but rather as a number of different chunks bought within each time period. The classical theory focuses on the selection of working hours and leisure, while extensions discuss the effect of various costs on working at home, outside the home, and acquiring education. However, the theory cannot explain the fact that most people separate their consumption into smaller chunks although this would sometimes increase the cost of consumption to a large degree. We show that if we apply classical theory when taking into consideration the cut of consumption into smaller chunks, we get absurd results, in which consumers consume non-optimal baskets.

According to the model we present in this paper, utility from consumption is affected not only by the amount of consumption, but also by the ability to cut consumption into smaller chunks.

The consumer agrees to give up some of the consumption in exchange for the ability to cut it into smaller chunks. Given this new concept of utility, the consumer is making two different decisions: the first is how many hours to work―which defines his income which equals his consumption if he were to consume it all in one chunk, while the second is into how many chunks to cut consumption in order to maximize utility from consumption.

We present an example that demonstrates the idea and emphasizes the fact that cutting consumption into smaller chunks can be explained by the higher utility that the consumer gets from consuming smaller chunks, an additional utility that compensates him for the higher costs when buying smaller bundles.

Cite this paper

Ben DavidNissim,BenzionUri, (2015) The Cost and Benefit of Consuming in Smaller Bundles. Theoretical Economics Letters,05,599-605. doi: 10.4236/tel.2015.55070

References