ABSTRACT

We derive two forms of Roy’s identity for a dynamic consumption model. The results are potentially useful in theoretical and empirical studies.

Keywords: Roy’s Identity, Inter-Temporal Consumption

1. Introduction

Roy’s identity is a useful tool in theoretical and empirical studies of static consumption problems. Most dynamic consumer problems, however, concentrate on obtaining the optimal consumption path derived from the Euler equation. In this note we assume that the consumer makes decision in a two-stage process. In the dynamic stage, two forms of Roy’s identity are derived. The first form relates the asset holding in each period to the marginal utility of interest rate and the marginal utility of income. The second form resembles the classic Roy’s identity in the static analysis.

2. Dynamic Roy’s Identity

The consumer is supposed to be making a two-stage decision. In the first stage, an inter-temporal decision on aggregate consumption and saving is made. Abstract from uncertainty about the future, a simple model of the decision problem can be set up as

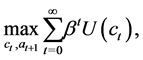(1)

subject to the budget constraints

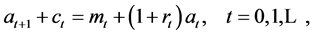(2)

where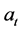, , 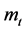and 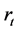are exogenous asset, income, and interest rate respectively in period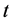, with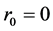. The choice variables are 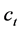and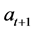. Utility is modelled by a stationary and separable discounted sum of utility function 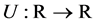in each period1. The Lagrangian is

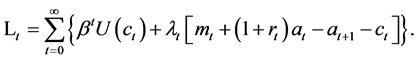(3)

The first-order conditions are

(4)

and the budget constraint (2).

The optimal solution is characterized by the Euler equation

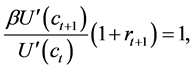(5)

and the consumption function (in the case of constant interest rate)

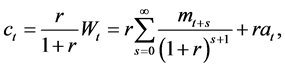(6)

which implies that in the steady state consumption in each period is a fixed portion of total wealth. The indirect utility function 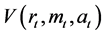is obtained by substituting in (6) into the objective function in (1).

In the second stage, the consumer makes decisions on how much to buy in number of goods and services in the market given the market prices and the aggregate consumption in each period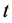. The model becomes the standard consumer optimization problem in microeconomics, that is,

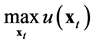(7)

subject to

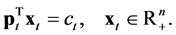
The indirect utility function in each period 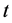is then

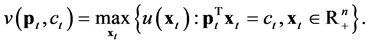
Roy’s identity relates the optimal consumption of each good or service to the marginal disutility of price and the marginal utility of income, that is,

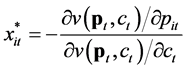
for every good 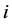in every period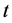. In other words, consumption of each good depends on the consumer’s preference structure and the relative price of the good to other goods and services.

Can we have Roy’s identity for the inter-temporal consumption problem in the first stage? Apply the envelop theorem to (3), we have

Substituting the first-order condition (4) into the above gives

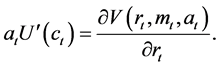(8)

Similarly,

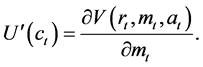(9)

Combining (8) and (9) gives the Roy’s identity for the inter-temporal consumption problem as

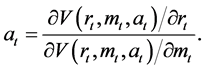
It says that in any period if the consumer is in debt, the marginal utility of an interest rate increase is negative.

A Roy’s identity similar to the static form can be obtained by considering the “cake-eating” problem by assuming that income 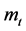in the budget constraint (2) in each period is zero. Then the inter-temporal budget constraint is reduced to

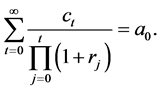
If we define

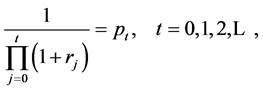
then the intertemporal utility maximization problem becomes

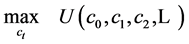
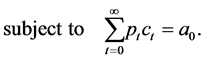
Notice that since. Starting in Period 1, price of consumption is decreasing over time due to discounting. The indirect utility function can be expressed as

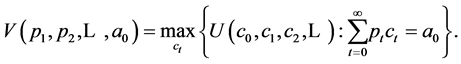
Roy’s identity, in this case, is

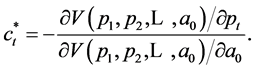
3. Conclusion

We have used the envelop theorem to derive two forms of Roy’s identity under an infinite horizontal consumption setting. In the first form, asset holding is related to the marginal utility of interest rate and marginal utility of income. The result can be used as a structural restriction on empirical analysis of inter-temporal consumption. In the second form prices are interpreted as future discount factors. The resulting form resembles the static Roy’s identity.

References

NOTES

¹See, for example, .