Theoretical Economics Letters
Vol.4 No.4(2014), Article ID:45231,7 pages DOI:10.4236/tel.2014.44036
Changes in the Threshold Uncertainty in a Simultaneous Subscription Game
Timothy J. Gronberg, Hui-Chun Peng
Department of Economics, Texas A&M University, College Station, USA
Email: tjg@econmail.tamu.edu, hpeng@econmail.tamu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 5 February 2014; revised 5 March 2014; accepted 25 March 2014
Abstract
This paper considers a discrete public good subscription game under threshold uncertainty and private information on valuations and analyzes the effect of change in cost uncertainty on the private contribution equilibrium under a simultaneous institution. Comparative statics with respect to the changes in the cost distribution are derived. We find that if the cost distribution becomes more dispersed, in the sense of a mean-preserving spread, the expected total contributions to the public good will decrease. Our proposition provides a policy implication that if the suppliers are able to reduce the uncertainty of the cost distribution, the private contribution to the public good will increase.
Keywords
Discrete Public Good, Threshold Uncertainty, Private Information

1. Introduction
This paper considers a model of provision of a discrete public good in a subscription game within an environment of threshold uncertainty and private information on public good valuations. The focus is on the comparative statics of a change in cost uncertainty on the private contribution equilibrium under a simultaneous institution. In a voluntary contributions mechanism, a discrete public good is provided if the total contributions are large enough to cover cost; otherwise, the public good is not provided. This kind of public good is also called a binary or a threshold public good. Typical examples of discrete public goods are roads, parks, community libraries, local radio programs, and school buildings. In a subscription game, the player contributions are refunded if the sum of the contributions does not cover the cost of the public good.
Palfrey and Rosenthal [1] and Bagnoli and Lipman [2] are important early papers that analyze private provision of discrete public good. Both papers assume players to make their contribution strategies in an environment with complete information on public good valuations and a certain known cost threshold, but the contribution types in these two papers are different. Palfrey and Rosenthal [1] assumed contributions to be binary—zero or a fixed contribution quantity, while Bagnoli and Lipman [2] allowed the players to make continuous contributions. These two papers both show that efficient provision of public goods in the subscription game may exist.
It is possible that the players do not face a certain threshold. For example, it might not be known how much money will be needed to build a community library or to complete a public good project. Realizing that the threshold uncertainty may affect the player’s strategic contribution behavior, Nitzan and Romano [3] , Suleiman [4] , and McBride [5] introduce threshold uncertainty into the discrete public good model. The first two papers find possibility of inefficient equilibrium under threshold uncertainty. The reason that inefficiency may obtain is that the ex post contributions exceed the required threshold quantity of contribution or the contributions are insufficient to cover the required threshold level. McBride [5] investigates how the level of threshold uncertainty affects players’ contributions and he finds that instead of having a monotonic relationship between the threshold uncertainty and the contributions, the effect of changing the threshold uncertainty on the contributions depends on public good valuations. An increase of the threshold uncertainty, in the sense of mean-preserving spread, increases the player’s contribution when the value of the public good is sufficiently high; otherwise, it decreases the player’s contribution when the value of the public good is sufficiently low. In a follow-up paper, McBride [6] designs an experiment to test the theoretical predictions in McBride [5] and finds limited verification.
Papers by Menezes et al. [7] , Laussel and Palfrey [8] , and Barbieri and Malueg [9] , introduce private information on public good valuations into a subscription game with a discrete public good and focus on examining the efficiency of the Bayesian Nash equilibrium. Menezes et al. [7] show that the equilibrium in the subscription game is ex post inefficient. Laussel and Palfrey [8] analyze interim incentive efficiency, defined by Holmstrŏm and Myerson [10] , in the subscription game. They find that the interim incentive efficient equilibrium may exist. Later, Barbieri and Malueg [9] reexamine Laussel and Palfrey’s analysis, but show the contrary result that there are no incentive efficient equilibria.
Barbieri and Malueg [11] include both threshold uncertainty and private information on public good valuations in the subscription game. They find that increased player valuation, in the sense of the first order stochastic dominance, or a more dispersed player value distribution, in the sense of a mean-preserving spread, increases the equilibrium contributions.
Although McBride [5] analyzes how the change of the threshold distribution affects the contribution, he only considers the model with identical and known public good valuation. Barbieri and Malueg [11] assume the threshold uncertainty and private information in their model, but they only analyze the effects of changing the valuation distribution. Our paper complements these existing papers by investigating the comparative statics effect of changing the cost distribution on private contributions within a Barbieri and Malueg setting with both threshold uncertainty and private information.
We show that if the cost distribution becomes more dispersed, in the sense of a mean-preserving spread, the expected contributions will decrease. Our results suggest that suppliers may increase contributions to the public good by reducing uncertainty over the cost distribution.
The rest of paper is organized as follows. Section 2 presents the model. Section 3 considers the comparative statics with respect to changes in cost distribution of the public good and characterizes the expected contribution. Section 4 is the conclusion.
2. Model
Consider a subscription game with  players. In order to provide a discrete public good, the players in this game simultaneously make contributions toward this public good of any non-negative amount. Let
players. In order to provide a discrete public good, the players in this game simultaneously make contributions toward this public good of any non-negative amount. Let  be player
be player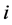 ’s contribution. Player
’s contribution. Player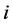 ’s value on the public good is
’s value on the public good is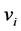 ,
,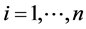 . Player’s value,
. Player’s value, 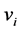 , is independently distributed random variables with a continuous uniform distribution whose support is [0, 1]. Each player’s valuation for the public good is private information. Each player knows his own realized valuation for the public good, but he is uncertain about other players’ valuations for the public good.
, is independently distributed random variables with a continuous uniform distribution whose support is [0, 1]. Each player’s valuation for the public good is private information. Each player knows his own realized valuation for the public good, but he is uncertain about other players’ valuations for the public good.
A discrete public good can be provided if and only if the total contributions are equal to or larger than the cost of the public good,  , which is also called the cost threshold. Suppose
, which is also called the cost threshold. Suppose  is unknown when the players contribute to the public good. However, all players believe that the cost is independent of all
is unknown when the players contribute to the public good. However, all players believe that the cost is independent of all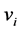 ’s and distributed with a continuous uniform distribution,
’s and distributed with a continuous uniform distribution,  , with support
, with support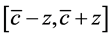 , where
, where  is the mean of the cost and
is the mean of the cost and  measures the degree of the cost uncertainty.
measures the degree of the cost uncertainty.
The public good game we consider in this paper is the subscription game (Admati and Perry [12] ), where player contributions will be fully refunded if the total contributions are less than the cost threshold. We also assume a zero rebate rule which means the excess contributions will be given to the producer of the public good.
Given , the ex ante probability of providing the public good with total contributions,
, the ex ante probability of providing the public good with total contributions,  , is
, is

Since the player does not know other players’ contributions when making the contribution decision, he needs to forecast the amounts other players will contribute,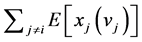 . Because the probability of provision should be between 0 and 1, it implies an important constraint,
. Because the probability of provision should be between 0 and 1, it implies an important constraint, 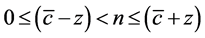 , must be satisfied1. This constraint demonstrates that the number of players in this subscription game need to be larger than the lower bound of the possible cost, but cannot be larger than the upper bound of the possible cost.
, must be satisfied1. This constraint demonstrates that the number of players in this subscription game need to be larger than the lower bound of the possible cost, but cannot be larger than the upper bound of the possible cost.
The assumed objective for each player is to maximize expected payoff. If the public good is provided, then player ’s payoff is
’s payoff is 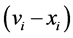 with the probability of the provision,
with the probability of the provision,
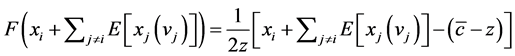
if the public good is not provided, then player i’s payoff is 0. Thus, player i’s expected payoff function can be written as:
 (1)
(1)
Assume  is player
is player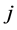 ’s expected contribution, thus, player
’s expected contribution, thus, player ’s expected utility function can be rewritten as:
’s expected utility function can be rewritten as:
 (2)
(2)
Maximizing Equation (2) with respect to  and taking the first order condition yields player
and taking the first order condition yields player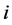 ’s best response function:
’s best response function:
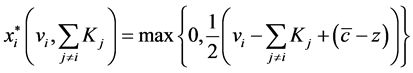 (3)
(3)
Under the assumption of a common uniform distribution in [0, 1], the total expected contributions by other players,  , can be written as
, can be written as 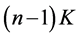 in symmetric equilibrium. Hence, Equation (3) can be rewritten as
in symmetric equilibrium. Hence, Equation (3) can be rewritten as
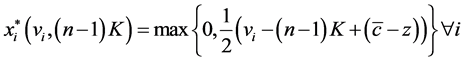 (4)
(4)
From the best response function, Equation (4), we can find that  is the cutoff point for player
is the cutoff point for player 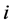 to begin contributing to the public good. In other words, player
to begin contributing to the public good. In other words, player 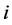 is willing to contribute a positive amount to the public good when his valuation for the public good is equal to or larger than this cutoff point. Also, the best response function shows that once player
is willing to contribute a positive amount to the public good when his valuation for the public good is equal to or larger than this cutoff point. Also, the best response function shows that once player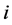 ’s contribution is positive, it is strictly increasing in larger valuation of the public good and strictly decreasing in other players’ expected contributions.
’s contribution is positive, it is strictly increasing in larger valuation of the public good and strictly decreasing in other players’ expected contributions.
Using the definition of expected contribution,  , and the best response function, Equation (4), in a symmetric Bayesian Nash equilibrium
, and the best response function, Equation (4), in a symmetric Bayesian Nash equilibrium
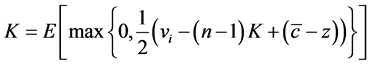 (5)
(5)
With player values independently and uniformly distributed on [0, 1], the expected equilibrium contribution is determined by
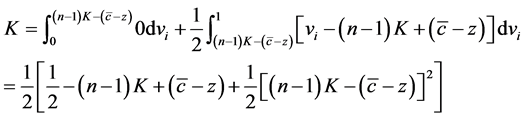 (6)
(6)
We can solve (6) for K which yields is
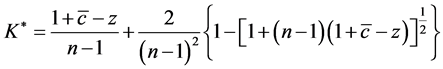 (7)
(7)
Player ’s equilibrium strategy,
’s equilibrium strategy,  , must be satisfied Equation (4), and
, must be satisfied Equation (4), and  is determined by Equation (7), therefore,
is determined by Equation (7), therefore, 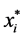 can be written as:
can be written as:
 (8)
(8)
The cutoff point in equilibrium for each player to begin contributing a positive amount to the public good, 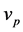 , is
, is
 (9)
(9)
Since the lower bound of player’s value is 0, vp has to be equal to or larger than 0. Thus, we can get a constraint that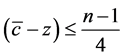 .
.
Figure 1 depicts player ’s equilibrium strategy.
’s equilibrium strategy.
3. Cost Threshold Comparative Statics
Players may confront cost distributions with different levels of dispersion. If the cost distribution can be controlled or affected by supplier actions, the results in this paper may suggest to the producer of the public good the benefits of changing information related to the cost of the public good measured in terms of increased expected total contribution to the public good. In this section we consider the effect of changes in the cost distribution on equilibrium contributions.
3.1. Mean-Preserving Spread in Cost Threshold Distribution
Given each player’s value distribution is followed a common uniform distribution over [0, 1], assume the cost distribution becomes more uncertain in the sense of mean-preserving spread. For example, the new cost distribution is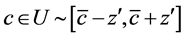 , where
, where .
.
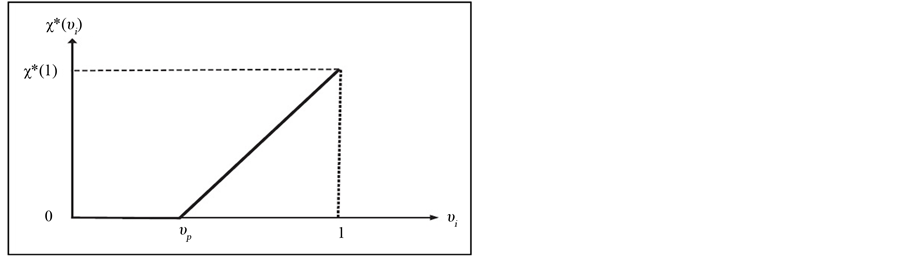
Figure 1. Cutpoint equilibrium strategy.
Proposition.
A mean-preserving increase in the distribution of cost will decrease the total expected contributions.
Proof.
From Equation (7), we know that 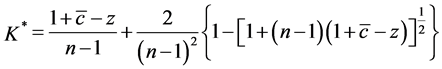 in equilibrium. Differentiating Equation (7) with respect to the degree of the cost uncertainty,
in equilibrium. Differentiating Equation (7) with respect to the degree of the cost uncertainty,  , we can get
, we can get
 (10)
(10)
Since  is the lower bound of the threshold and assuming
is the lower bound of the threshold and assuming ,
,  will be less than 1. Thus, we can obtain
will be less than 1. Thus, we can obtain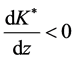 .
.
Since 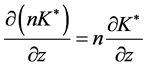 and we have shown
and we have shown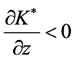 ,
, . Since the expected contribution per player decreases, so does the total expected contribution. ■
. Since the expected contribution per player decreases, so does the total expected contribution. ■
The proposition indicates that the players, on average, become less willing to contribute to the public good when the cost of the public good becomes more uncertain.
We have shown that the cutoff point in equilibrium is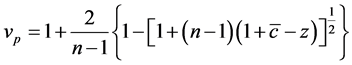 . When
. When 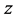
increases, the cutoff point will increase2. It means that the player will begin contributing a positive amount to the public good at a higher value as the degree of cost uncertainty increases.
The change in 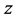 also affects the player’s best response function where
also affects the player’s best response function where , and this effect can be divided into the direct effect and the indirect effect. Using the player’s best response function,
, and this effect can be divided into the direct effect and the indirect effect. Using the player’s best response function,  , to demonstrate these two effects
, to demonstrate these two effects
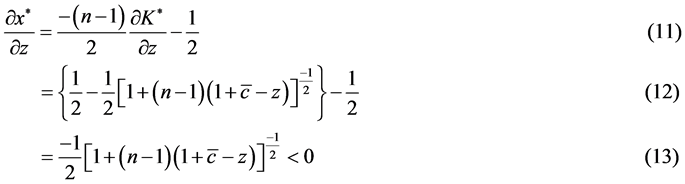
From Equation (11), we find that changing  will change
will change  directly, hence, the second term in Equation (11) can represent the direct effect. Also, changing
directly, hence, the second term in Equation (11) can represent the direct effect. Also, changing  will affect other players’ expected contributions,
will affect other players’ expected contributions, . The first term in Equation (11) measures this indirect effect. Equation (12) shows that increasing the degree of cost uncertainty induces a negative direct effect, a positive indirect effect, and the direct effect dominates the indirect effect. Thus, increasing
. The first term in Equation (11) measures this indirect effect. Equation (12) shows that increasing the degree of cost uncertainty induces a negative direct effect, a positive indirect effect, and the direct effect dominates the indirect effect. Thus, increasing  results in the decrease of
results in the decrease of .
.
We find that players start to contribute to the public goods at a higher cutpoint value and the contribution amounts at each possible value of public good weakly decrease, hence, the expected contribution to the public goods decreases in the degree of cost uncertainty, .
.
Our proposition provides a policy implication that if the suppliers are able to reduce the uncertainty of the cost distribution, the private contribution to the public good will increase. The reduction in cost distribution uncertainty will encourage the players with low value to begin contributing to the public good and also increase contributions of inframarginal contributors.

Figure 2. Expected contribution and mean-preserving spread of costs.
3.2. Numerical Example
In this subsection, we use a numerical example to illustrate that expected contribution,  , decreases in
, decreases in .
.
Example.
In this example, we consider a subscription game with 5 players whose values are uniformly distributed in [0, 1]. Also, we assume that players do not know the cost of providing the public good but believe it is drawn from a uniform distribution with support [1, 5], i.e. the initial 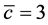 and
and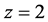 . If the cost distribution becomes more dispersed in the sense of mean-preserving spread, such as
. If the cost distribution becomes more dispersed in the sense of mean-preserving spread, such as  increases from 2 to 2.2, Figure 2 shows that the expected contribution is decreasing in
increases from 2 to 2.2, Figure 2 shows that the expected contribution is decreasing in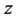 .
.
4. Conclusions
If the valuation for the public good is complete information and identical for each player, McBride (2006) finds that the effects of increased cost uncertainty depend on the value of the public good. However, when we consider public good valuations as private information that expected contributions are monotonic and that a more dispersed cost distribution always decreases the expected contributions.
From a policy aspect, we suggest that supplier may increase the private contribution to the public good, if they can reduce the degree of uncertainty with respect to the cost distribution when both threshold uncertainty and private information on public good valuations exist.
We offer two directions for future research. Many real-world private contribution institutions are not simultaneous. Contributions are instead collected sequentially. For example, churches may announce organ fund campaign and report the updated contribution level frequently or local governments announce the seed donations to future contributors when they launch new public good projects. There is no published research that investigates how the sequential contribution would be affected by a change in the dispersion of the cost distribution or the value distribution in a subscription game under the threshold uncertainty and private information of valuation for the public good. A second research direction is to test the hypothesis from our theoretical model using experimental methods in a laboratory environment. These future studies may result in a more complete understanding of behavior in mechanisms of private contribution to public goods.
Acknowledgements
We have benefited from comments by Silvana Krasteva and participants at Ph.D. Student Presentation Seminar at Texas A&M University. We also thank anonymous referees for their comments. All errors are our own.
References
- Palfrey, T. and Rosenthal, H. (1984) Participation and the Provision of Discrete Public Goods: A Strategic Analysis. Journal of Public Economics, 24, 171-193. http://dx.doi.org/10.1016/0047-2727(84)90023-9
- Bagnoli, M. and Lipman, B. (1989) Provision of Public Goods: Fully Implementing the Core through Private Contributions. The Review of Economic Studies, 56, 583-601. http://dx.doi.org/10.2307/2297502
- Nitzan, S. and Romano, R.E. (1990) Private Provision of a Discrete Public Good with Uncertain Cost. Journal of Public Economics, 42, 357-370. http://dx.doi.org/10.1016/0047-2727(90)90021-9
- Suleiman, R. (1997) Provision of Step-Level Public Goods under Uncertainty: A Theoretical Analysis. Rationality and Society, 9, 163-187. http://dx.doi.org/10.1016/0047-2727(90)90021-9
- McBride, M. (2006) Discrete Public Goods under Threshold Uncertainty. Journal of Public Economics, 90, 1181-1199. http://dx.doi.org/10.1016/j.jpubeco.2005.09.012
- McBride, M. (2010) Threshold Uncertainty in Discrete Public Good Games: An Experimental Study. Economics of Governance, 11, 77-99. http://dx.doi.org/10.1007/s10101-009-0069-8
- Menezes, F.M., Monteiro, P.K. and Temimi, A. (2001) Private Provision of Discrete Public Goods with Incomplete Information. Journal of Mathematical Economics, 35, 493-514. http://dx.doi.org/10.1016/S0304-4068(01)00059-3
- Laussel, D. and Palfrey, T.R. (2003) Efficient Equilibria in the Voluntary Contributions Mechanism with Private Information. Journal of Public Economic Theory, 5, 449-478. http://dx.doi.org/10.1111/1467-9779.00143
- Barbieri, S. and Malueg, D.A. (2008) Private Provision of a Discrete Public Good: Continuous-Strategy Equilibria in the Private-Information Subscription Game. Journal of Public Economic Theory, 10, 529-545. http://dx.doi.org/10.1111/j.1467-9779.2008.00375.x
- Holmstrŏm, B. and Myerson, R.B. (1983) Efficient and Durable Decision Rules with Incomplete Information. Econometrica, 51, 1799-1820. http://dx.doi.org/10.2307/1912117
- Barbieri, S. and Malueg, D.A. (2010) Threshold Uncertainty in the Private-Information Subscription Game. Journal of Public Economics, 94, 848-861. http://dx.doi.org/10.1016/j.jpubeco.2010.07.003
NOTES

1Since , we can get
, we can get . Also, we have assumed that
. Also, we have assumed that  and
and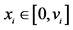 , thus,
, thus, 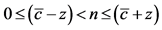 must be satisfied.
must be satisfied.

2Since ,
, 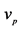 increases when
increases when  increases.
increases.

