Theoretical Economics Letters
Vol.4 No.1(2014), Article ID:42791,6 pages DOI:10.4236/tel.2014.41001
Some Properties of the Technology Gap between Leading and Lagging Regions
1Department of Economics, Rochester Institute of Technology, Rochester, USA
2Department of Spatial Economics, VU University, Amsterdam, The Netherlands
Email: aabgsh@rit.edu, p.nijkamp@vu.nl
Copyright © 2014 Amitrajeet A. Batabyal, Peter Nijkamp. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Amitrajeet A. Batabyal, Peter Nijkamp. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received September 5, 2013; revised October 5, 2013; accepted October 12, 2013
KEYWORDS
Economic Growth; Lagging Region; Leading Region; Technology Gap
ABSTRACT
We theoretically analyze some properties of the technology gap between leading and lagging regions studied recently by Batabyal and Nijkamp [1]. New technologies are developed in the leading region. The lagging region does not conduct research and development (R & D) but uses the leading region’s technology with a temporal gap of  > 0 time periods. We first use a model with a single factor of production, human capital, to study the relationship between the technology gap
> 0 time periods. We first use a model with a single factor of production, human capital, to study the relationship between the technology gap  and the difference in the growth rates of output per human capital unit in the leading and in the lagging region. Next, we introduce a second factor of production, physical capital, and use a variant of the Solow growth model to shed light on two issues. We show that despite the existence of the technology gap, on the balanced growth path (BGP), the physical to effective human capital ratio is identical in both regions. Finally, we demonstrate that introducing a second factor of production does not alter the relationship between the technology gap
and the difference in the growth rates of output per human capital unit in the leading and in the lagging region. Next, we introduce a second factor of production, physical capital, and use a variant of the Solow growth model to shed light on two issues. We show that despite the existence of the technology gap, on the balanced growth path (BGP), the physical to effective human capital ratio is identical in both regions. Finally, we demonstrate that introducing a second factor of production does not alter the relationship between the technology gap  and the difference in the growth rates of output per human capital unit in the two regions.
and the difference in the growth rates of output per human capital unit in the two regions.
1. Introduction
The process of economic growth in regions frequently does not lead to balanced growth. Looking at countries, it is fair to say that irrespective of whether one focuses on a developed or a developing country, there are inequalities of various sorts between the regions that comprise the country under consideration. This understanding has led to considerable interest in studying the characteristics of so called “leading” and “lagging” regions. In this twopart classification, leading regions are generally dynamic, frequently urban, they display relatively rapid rates of economic growth, and they are technologically more advanced. In contrast, lagging regions are generally not as dynamic, they are often rural or peripheral, they display slow economic growth rates, and they are technologically backward.
In an early paper, Ghosh and De [2, p. 391] focus on the metric of income and note that there are clear differences in incomes between the leading and the lagging states in India. Their empirical analysis suggests that these income differences can be addressed by the government “undertaking large infrastructure projects in lagging regions.” Kalirajan [3] also focuses on India and notes that if one is to boost economic growth and promote growth spillovers from the leading to the lagging states, then it is essential to pay attention to the quality of human capital in the various states.
Desmet and Ortin [4] study uneven development in a model with two regions and two sectors. They show that because there is uncertainty about which region benefits from technological change, it may make sense for the lagging region to remain underdeveloped. The connection between leading and lagging regions in Brazil is the focus of Lall, Timmins, and Yu [5]. These researchers point out that in addition to encouraging the formation of human capital, policies that increase welfare will need to improve access to and the quality of basic services in the lagging regions.
In addition to this literature on leading and lagging regions, a related literature has now emerged on the “technology gap” between regions where the regions under study are geographical entities that may be either bigger than or smaller than countries. In this regard, Nocco [6] analyzes leading and lagging regions in terms of their initial technological gap and differences in what she calls trade costs. She studies conditions for the existence of interregional knowledge spillovers and notes that high trade costs result in the agglomeration of the modern sector in the leading region. Using a multi-country model, Sadik [7] shows that although technological progress diminishes differences within the group of countries that adopt the underlying technologies, this progress also increases the gap between the adopting countries and the rest of the world.
Castellacci [8] uses a dynamic panel model specification to estimate what he calls a technology gap growth equation. This exercise shows that for the countries being studied, there are three technology clubs and they are characterized by very different technological attributes and growth behavior. Finally, using a North-South modeling framework, Borota [9] shows that when the imitation technology in the South is a function of the increasing complexity of the targeted products, the move from autarky to free trade results in a larger North-South quality gap.
The various studies discussed in the preceding four paragraphs have certainly advanced our understanding of the working of leading and lagging regions and the notion of a technology gap between these regions. Even so, to the best of our knowledge, there are very few theoretical studies that explicitly link the trinity of human capital, technology, and learning when studying the economic growth prospects of leading and lagging regions. In this regard, Batabyal and Nijkamp [1] have recently analyzed a dynamic model of technology transfer between a leading and a lagging region where the transfer is the result of the lagging region learning the technology of the leading region. In this setting, Batabyal and Nijkamp [1] define a lagging to leading region technology ratio, study its stability properties, and then use this ratio to ascertain the long run growth rate of output per human capital unit in the lagging region. Although the gap in the technology possessed by the leading and the lagging regions is a distinct feature of the Batabyal and Nijkamp [1] analysis, these authors do not explicitly analyze the properties of this technology gap. Given this lacuna in the literature, our objective in this paper is to theoretically analyze some properties of the technology gap between stylized leading and lagging regions.
Our modeling framework is described in Section 2. In this framework, new technologies are developed in the leading region. The lagging region does not conduct research and development (R & D) but uses the leading region’s technology with a temporal gap of 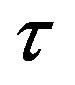 > 0 time periods. In what follows, without loss of generality, we shall think of a time period as corresponding to one calendar year. In Section 3, we use a model with a single factor of production, i.e., human capital, to study the relationship between the technology gap
> 0 time periods. In what follows, without loss of generality, we shall think of a time period as corresponding to one calendar year. In Section 3, we use a model with a single factor of production, i.e., human capital, to study the relationship between the technology gap 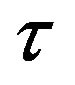 and the difference in the growth rates of output per human capital unit in the leading and in the lagging region. In Section 4, we introduce a second factor of production, i.e., physical capital, and use a variant of the Solow growth model to shed light on two issues. We show that despite the presence of the technology gap, on the balanced growth path (BGP), the physical to effective human capital ratio is identical in both regions. Next, we demonstrate that introducing a second factor of production does not alter the relationship between the technology gap
and the difference in the growth rates of output per human capital unit in the leading and in the lagging region. In Section 4, we introduce a second factor of production, i.e., physical capital, and use a variant of the Solow growth model to shed light on two issues. We show that despite the presence of the technology gap, on the balanced growth path (BGP), the physical to effective human capital ratio is identical in both regions. Next, we demonstrate that introducing a second factor of production does not alter the relationship between the technology gap 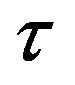 and the difference in the growth rates of output per human capital unit in the two regions, studied in Section 3. Finally, Section 5 concludes and then discusses potential extensions of the research delineated in this paper.
and the difference in the growth rates of output per human capital unit in the two regions, studied in Section 3. Finally, Section 5 concludes and then discusses potential extensions of the research delineated in this paper.
2. The Theoretical Framework
Consider a stylized, aggregate economy consisting of a leading and a lagging region. We index these two regions with the subscript i where i = L, F. The subscript L denotes the leading region and the subscript F denotes the lagging or following region. In the model analyzed in Section 3, human capital Hi(t) is the only exogenous factor of production in both the regions under study at any time t. In contrast, in the Section 4 model, in addition to human capital Hi(t), physical capital Ki(t) is the second exogenous factor of production in the two regions being studied.
In Section 3, there is no growth in the stock of human capital in either region. However, this assumption is dispensed with in Section 4 and the stocks of both human and physical capital evolve over time in accordance with Equations (11) and (12) given below. The technology or the stock of knowledge available in the two regions at any time t is denoted by Ai(t). The fraction of the human capital stock in the leading region that is employed in R & D is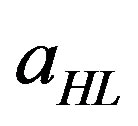 . Hence, (1‒aHL) is the fraction employed in the final good sector. With this background in place, we now analyze the technology gap between the leading and the lagging regions when the output of the single final good in each region is produced with technology and human capital only.
. Hence, (1‒aHL) is the fraction employed in the final good sector. With this background in place, we now analyze the technology gap between the leading and the lagging regions when the output of the single final good in each region is produced with technology and human capital only.
3. The Technology Gap with Human Capital
Output of the single final good in the leading region at any time t or 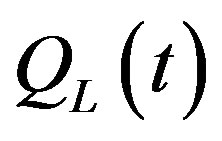 is produced in accordance with the production function
is produced in accordance with the production function
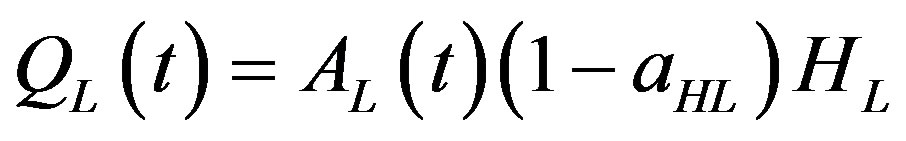 . (1)
. (1)
The available technology in the leading region evolves over time in accordance with the differential equation given by
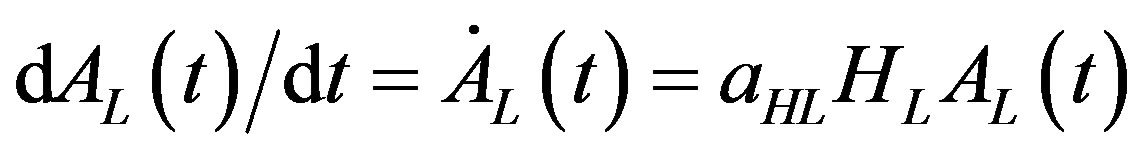 . (2)
. (2)
The lagging region does not conduct its own R & D. Instead, it simply uses the technology developed in the leading region. The important point to grasp now is that there is a temporal gap of 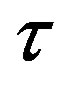 > 0 years between the time when the technology is developed and used in the leading region and when this same technology is actually utilized in the lagging region. We model this state of affairs formally in two ways. First, the output of the single final good in the lagging region at any time t is produced in accordance with
> 0 years between the time when the technology is developed and used in the leading region and when this same technology is actually utilized in the lagging region. We model this state of affairs formally in two ways. First, the output of the single final good in the lagging region at any time t is produced in accordance with
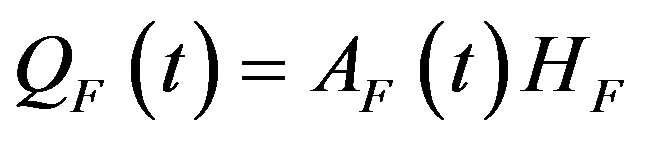 . (3)
. (3)
Second, the technology in the lagging region is given simply by
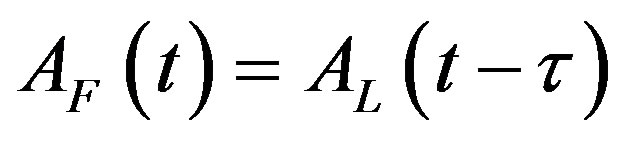 . (4)
. (4)
Now suppose that the growth rate of output per human capital unit in the leading region is x% per year. Also, to keep the subsequent analysis straightforward, suppose that the fraction of the human capital stock in the leading region that is employed in the final good sector or (1‒aHL) is close to one. We now want to know the value of 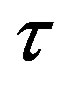 if output per human capital unit in the leading region exceeds that in the lagging region by a factor of, say, five.
if output per human capital unit in the leading region exceeds that in the lagging region by a factor of, say, five.
To answer the question in the preceding paragraph, we need to find a value of 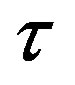 such that the ratio of output per human capital unit in the leading to the lagging region or
such that the ratio of output per human capital unit in the leading to the lagging region or 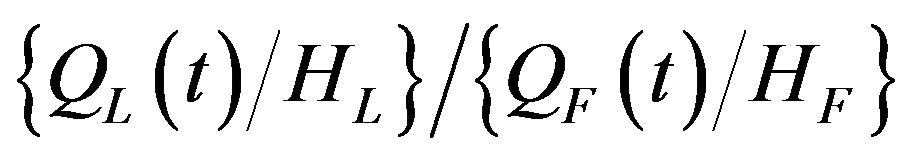 is equal to five. To this end, from equation (1) we deduce that
is equal to five. To this end, from equation (1) we deduce that
 . (5)
. (5)
Let us now take the natural logarithm of Equation (5) and then differentiate the resulting expression with respect to time. This gives us the following expression for the growth rate of output per human capital unit in the leading region
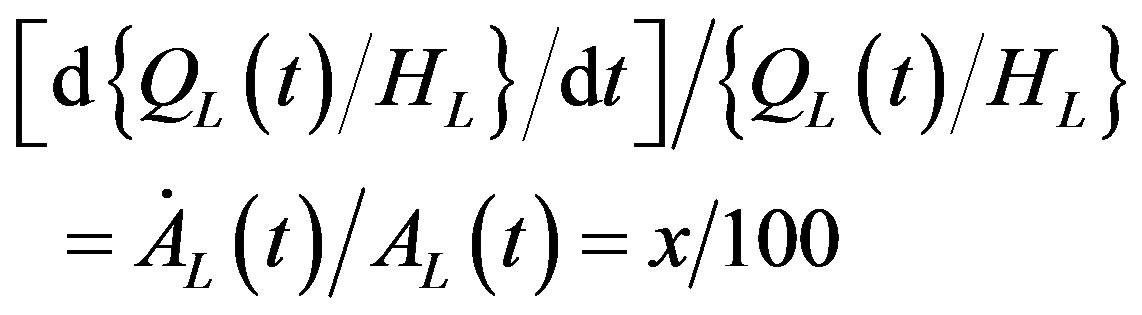 . (6)
. (6)
In writing Equation (6) we have used our assumption that the growth rate of output per human capital unit in the leading region is x% per year.
Simplifying the right-hand-side (RHS) of Equation (6), it is clear that
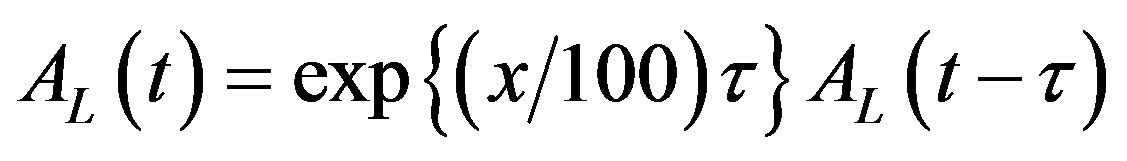 . (7)
. (7)
Rewriting Equation (3), we get
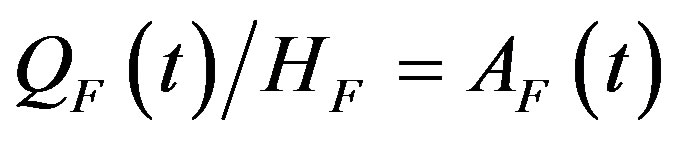 . (8)
. (8)
Dividing Equation (7) by Equation (8), using Equations (4) and (5), gives us an expression for the ratio of output per human capital unit in the leading region to that in the lagging region. That expression is
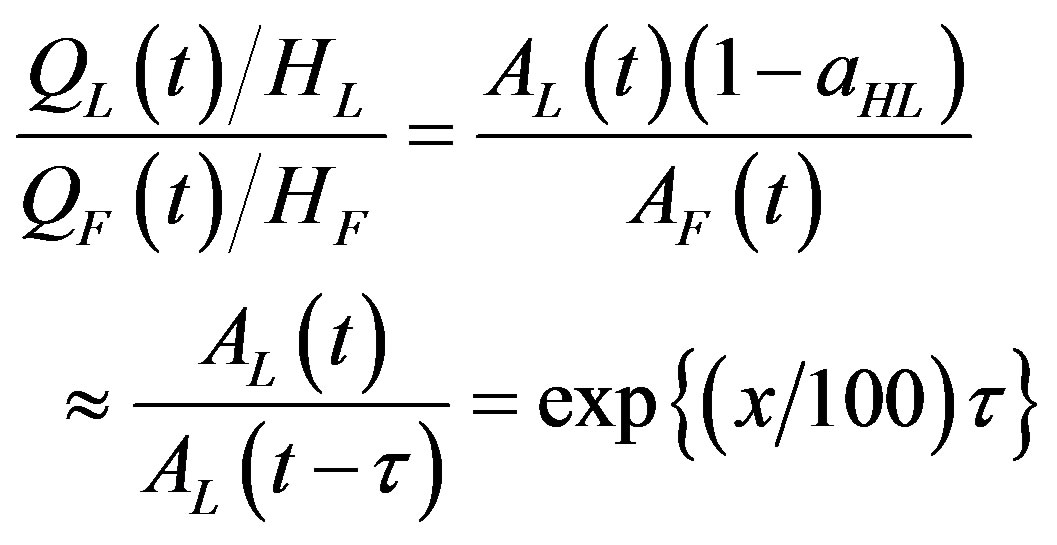 (9)
(9)
The reader will note that in writing Equation (9), we have used our assumption that (1‒aHL) ≈ 1 and Equations (4) and (7).
For output per human capital unit in the leading region to exceed the corresponding ratio in the lagging region by a factor of five, we must have a 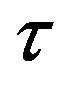 with the property that
with the property that
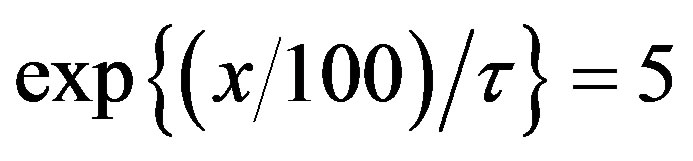
or
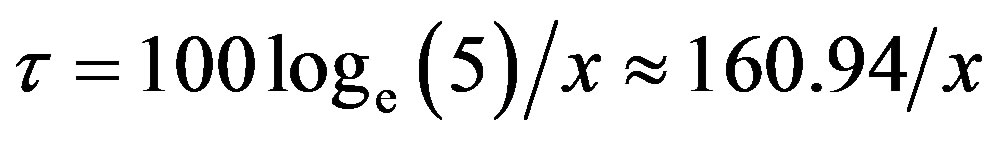 .
.
To make further progress, we will need an explicit value for x. As such, suppose x = 4. This means that the growth rate of output per human capital unit in the leading region is 4% per year. In this case, simple arithmetic tells us that 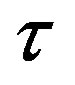 ∙160.94/4.40 years. This example tells us that if we are to explain a five-fold difference in output per human capital unit between the leading and the lagging regions, then the technology being used by the lagging region to produce output of the final good now, i.e., in 2013 is that which was developed and used in the leading region in 1973.
∙160.94/4.40 years. This example tells us that if we are to explain a five-fold difference in output per human capital unit between the leading and the lagging regions, then the technology being used by the lagging region to produce output of the final good now, i.e., in 2013 is that which was developed and used in the leading region in 1973.
As a second example, suppose that the growth rate of output per human capital unit in the leading region is 5% per year. We now want to know the value of 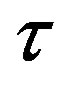 when output per human capital unit in the leading region exceeds that in the lagging region by a factor of, say, ten. Once again, simple computations tell us that
when output per human capital unit in the leading region exceeds that in the lagging region by a factor of, say, ten. Once again, simple computations tell us that  = 100loge(10)/5 ≈ 46 years. Using the year 2013 as our reference point, this second example tells us that the lagging region will now be using technology developed and used by the leading region in 1967 in order to explain a ten-fold difference in output per human capital unit in these two regions. We now use a variant of the Solow growth model and ask how the basic result of this section changes when, in addition to human capital, physical capital is also used to produce the output of the single final good in each of the two regions under study.
= 100loge(10)/5 ≈ 46 years. Using the year 2013 as our reference point, this second example tells us that the lagging region will now be using technology developed and used by the leading region in 1967 in order to explain a ten-fold difference in output per human capital unit in these two regions. We now use a variant of the Solow growth model and ask how the basic result of this section changes when, in addition to human capital, physical capital is also used to produce the output of the single final good in each of the two regions under study.
4. A BGP Value and the Technology Gap with Human and Physical Capital
We now suppose that the leading and the lagging regions can both be described by a variant of the Solow growth model1. This means that written in “intensive form,” output in the two regions can be delineated by the production function
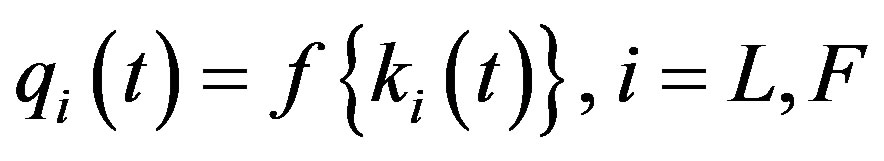 , (10)
, (10)
where 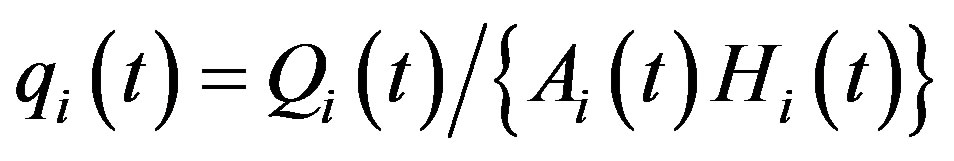 is the output per effective human capital input in each region and
is the output per effective human capital input in each region and 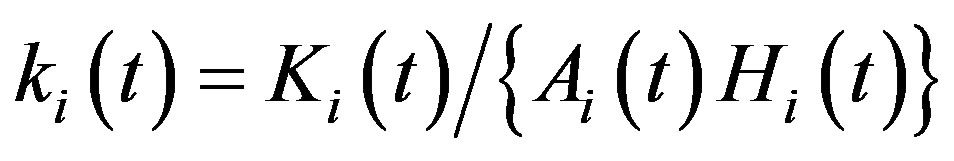 is the physical capital per effective human capital unit in each region. Note that the intensive production function
is the physical capital per effective human capital unit in each region. Note that the intensive production function 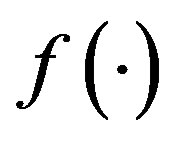 in Equation (10) has no subscript and hence is identical across the leading and the lagging region.
in Equation (10) has no subscript and hence is identical across the leading and the lagging region.
Consistent with the standard formulation in the Solow growth model, we suppose that the temporal evolution of the stock of human capital in both the regions is given by
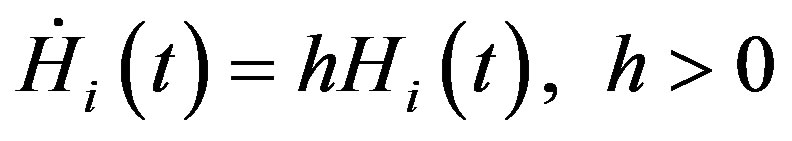 , (11)
, (11)
where the constant rate of growth of the human capital stock h > 0 is identical across the leading and the lagging region. Similarly, the stock of physical capital in the two regions evolves over time in accordance with
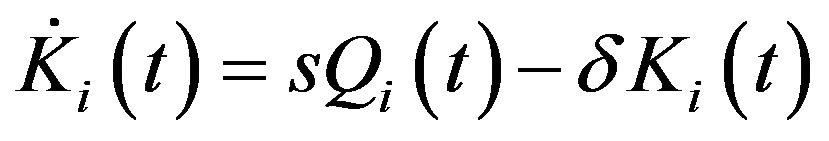 , (12)
, (12)
where s > 0 is the constant savings rate and δ > 0 is the constant depreciation rate. Note that like the human capital stock growth rate in Equation (11), the savings and the depreciation rates in Equation (12) are identical across the two regions being studied. Finally, the evolution of technology in the two regions is described by
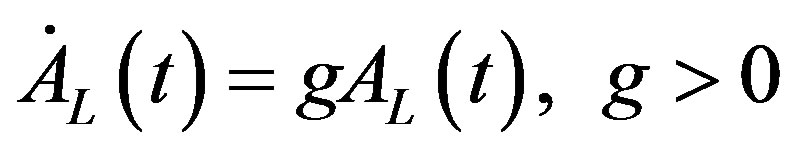 , (13)
, (13)
for the leading region and by Equation (4) for the lagging region. The coefficient g in Equation (13) is the constant rate of technological progress in the leading region.
4.1. The Physical Capital to Effective Human Capital Ratio on the BGP
Now, before we study whether the Section 3 result about the technology gap changes in the new setting of this section, let us first analyze what impact the technology gap between the leading and the lagging regions has on the balanced growth path (BGP) value of ki(t) or 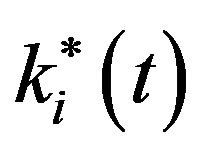 in each region. Adapting aspects of Acemoglu’s [11, pp. 26-76] analysis of the Solow growth model to our context, we deduce that on the BGP, the value of ki(t), denoted by
in each region. Adapting aspects of Acemoglu’s [11, pp. 26-76] analysis of the Solow growth model to our context, we deduce that on the BGP, the value of ki(t), denoted by 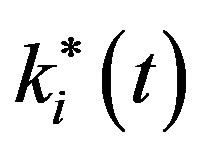 is given implicitly by the equation
is given implicitly by the equation
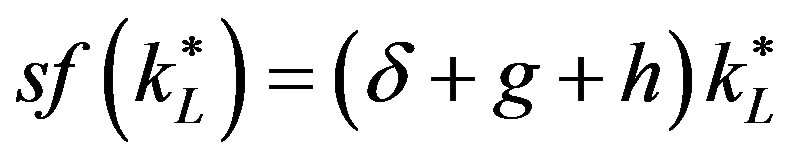 , (14)
, (14)
where from Equation (13) it follows that  .
.
From the preceding discussion in this section, we know that the function  and the parameters
and the parameters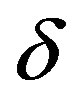 , g, and h are identical across the leading and the lagging region. This means that on the production side, the only possible source of difference in these two regions stems from the growth rate of technological knowledge in the lagging region. As such, let us determine this growth rate or
, g, and h are identical across the leading and the lagging region. This means that on the production side, the only possible source of difference in these two regions stems from the growth rate of technological knowledge in the lagging region. As such, let us determine this growth rate or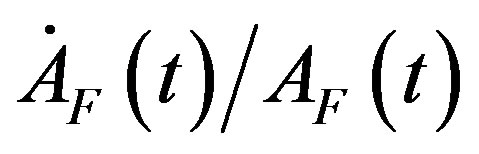 .
.
We know that the technology used in the lagging region at any time t is the technology developed and used in the leading region at time t‒ . Therefore, we have Equation (4) which we now re-write as
. Therefore, we have Equation (4) which we now re-write as
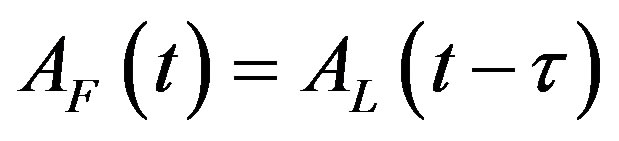 . (15)
. (15)
Differentiating Equation (15) with respect to time, we get
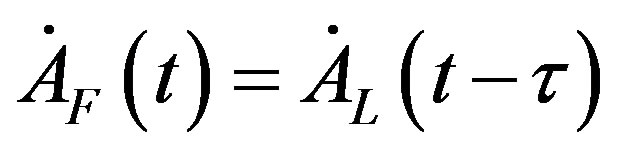 . (16)
. (16)
Dividing Equation (16) by Equation (15) gives us
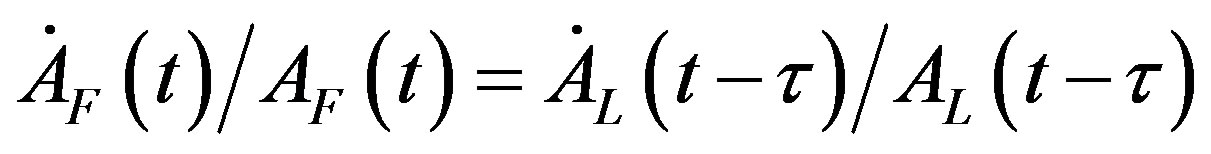 . (17)
. (17)
From Equation (13) we know that the rate of technological progress in the leading region is equal to g at all points in time. Using this fact in Equation (17) we conclude that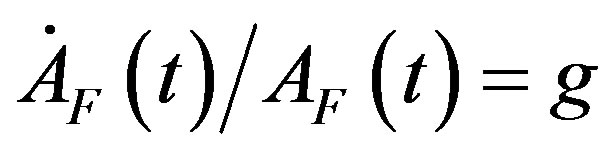 . This last result tells us that the equivalent of Equation (14) must hold in the lagging region as well. In other words, we must have
. This last result tells us that the equivalent of Equation (14) must hold in the lagging region as well. In other words, we must have
 . (18)
. (18)
Inspecting Equations (14) and (18), we infer that since 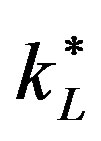 and
and  are defined implicitly by the same equation, they are, in fact, equal. Therefore, we conclude that even though there exists a technology gap between the leading and the lagging regions, on the BGP, the physical to effective human capital ratio is identical in both regions.
are defined implicitly by the same equation, they are, in fact, equal. Therefore, we conclude that even though there exists a technology gap between the leading and the lagging regions, on the BGP, the physical to effective human capital ratio is identical in both regions.
4.2. The Technology Gap with Two Factors of Production
To see if the introduction of physical capital alters the basic property of the technology gap we discussed in Section 3, let us note the following two points. First, to be consistent with the discussion in Section 3, the g in Equation (13) is now assumed to be x% per year. Second, from the analysis in Section 4.1, it follows that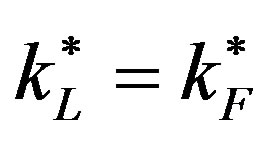 .. Because these last two ratios are equal, we deduce that output of the final good per effective unit of human capital in the two regions is also equal on the BGP. In symbols, we have
.. Because these last two ratios are equal, we deduce that output of the final good per effective unit of human capital in the two regions is also equal on the BGP. In symbols, we have
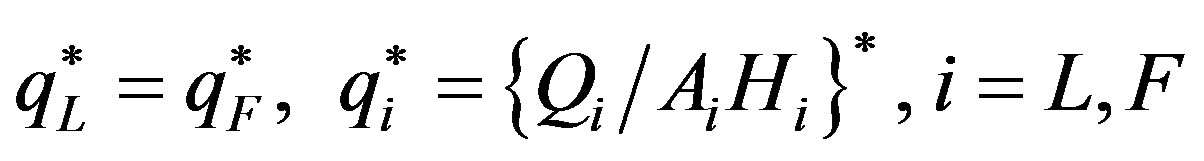 . (19)
. (19)
Given Equation (19), we can write the BGP value of output per effective human capital unit in the leading region as
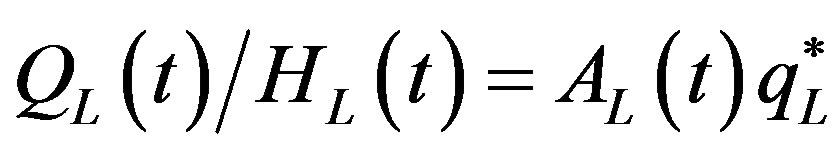 . (20)
. (20)
Similarly, the BGP value of output per effective human capital unit in the lagging region can be expressed as
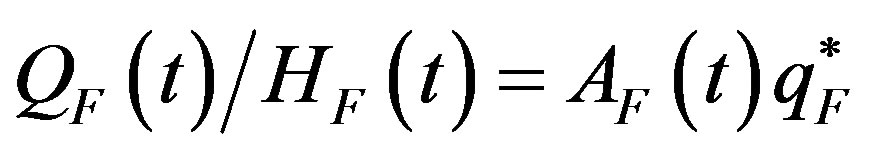 . (21)
. (21)
We now divide Equation (20) by Equation (21) and use the facts that 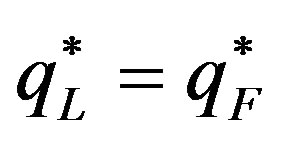 and
and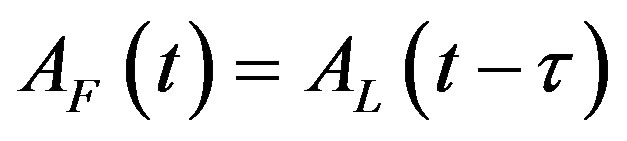 . This gives us
. This gives us
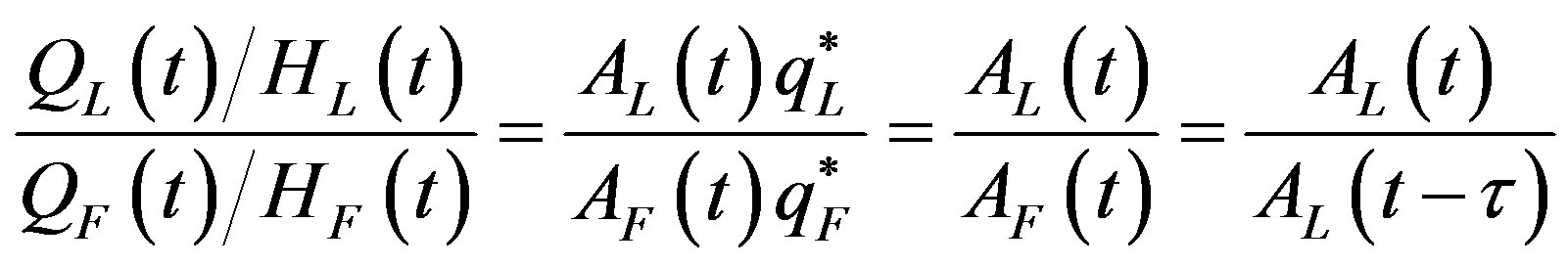 (22)
(22)
Substituting Equation (7) in the RHS of Equation (22) above, we get
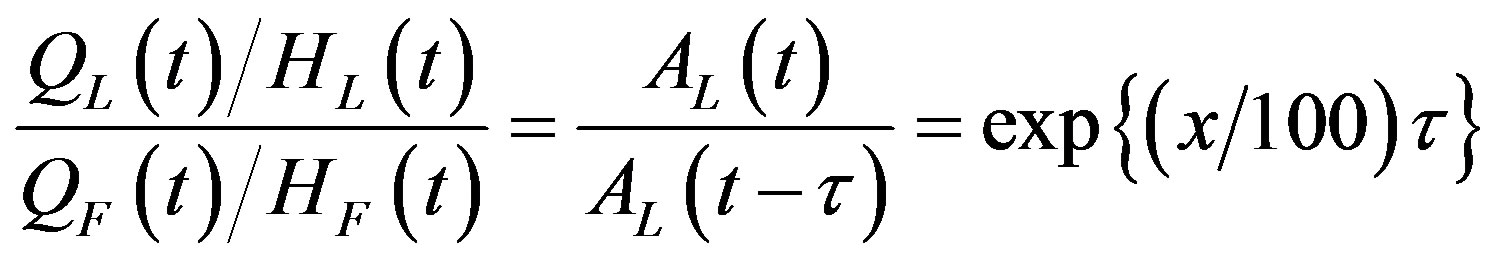 . (23)
. (23)
Given specific values for 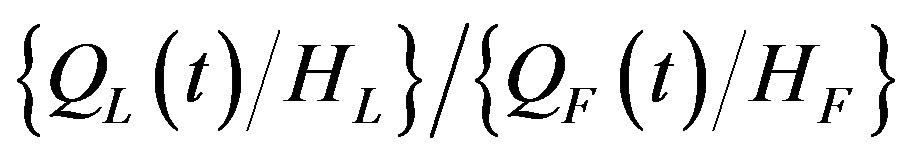 and x, the same computations as those undertaken previously show that the basic property of the technology gap between the leading and the lagging regions discussed in Section 3 does not change when we introduce a second factor, i.e., physical capital into the analysis. To see this concretely, recall that in the first example in Section 3—see the penultimate paragraph in Section 3—we had
and x, the same computations as those undertaken previously show that the basic property of the technology gap between the leading and the lagging regions discussed in Section 3 does not change when we introduce a second factor, i.e., physical capital into the analysis. To see this concretely, recall that in the first example in Section 3—see the penultimate paragraph in Section 3—we had 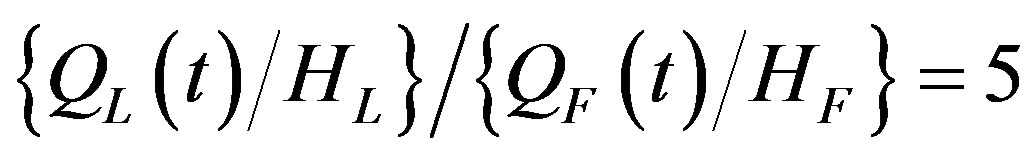 and x = 4. Using these two values in Equation (23), it is clear that as in Section 3, we once again get
and x = 4. Using these two values in Equation (23), it is clear that as in Section 3, we once again get 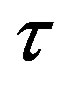 ≈ 40 years. This concludes our theoretical discussion of some properties of the technology gap between stylized leading and lagging regions.
≈ 40 years. This concludes our theoretical discussion of some properties of the technology gap between stylized leading and lagging regions.
5. Conclusions
In this paper, we studied two models describing the technology gap between a leading and a lagging region. In both models, new technologies were developed in the leading region. The lagging region did not conduct its own R & D but instead used the leading region’s technology with a temporal gap of 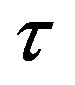 > 0 years. We used the model with human capital only to characterize the formal relationship between the technology gap
> 0 years. We used the model with human capital only to characterize the formal relationship between the technology gap 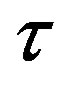 and the difference in the growth rates of output per human capital unit in the leading and in the lagging regions. Next, we introduced physical capital into the analysis and used a variant of the Solow growth model to shed light on two issues. We showed that on the BGP, the physical to effective human capital ratio was identical in both regions. Finally, we demonstrated that introducing physical capital into the analysis did not change the relationship between the technology gap
and the difference in the growth rates of output per human capital unit in the leading and in the lagging regions. Next, we introduced physical capital into the analysis and used a variant of the Solow growth model to shed light on two issues. We showed that on the BGP, the physical to effective human capital ratio was identical in both regions. Finally, we demonstrated that introducing physical capital into the analysis did not change the relationship between the technology gap 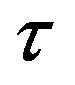 and the difference in the growth rates of output per human capital unit in the two regions under study. Consequently, the inertia in the change in spatial disparities seems to be a persistent trend in regional dynamics.
and the difference in the growth rates of output per human capital unit in the two regions under study. Consequently, the inertia in the change in spatial disparities seems to be a persistent trend in regional dynamics.
The analysis in this paper can be extended in a number of different directions. Here are two possible extensions. First, one could study a scenario in which the technology used in the lagging region is behind that used in the leading region by a stochastic number of time periods. Second, it would be helpful to analyze the properties of the aforementioned technology gap when technological progress or knowledge accumulation in the leading region is a byproduct of the production of one or more final goods. Studies that incorporate these aspects of the problem into the analysis will increase our understanding of the nexuses between technology, technology transfer, and economic growth in leading and lagging regions.
Acknowledgements
Batabyal thanks Cassandra Shellman for her help in formatting the paper and he acknowledges financial support from the Gosnell endowment at RIT. The usual disclaimer applies.
REFERENCES
- A. A. Batabyal and P. Nijkamp, “Technology, Learning, and Long Run Economic Growth in Leading and Lagging Regions,” Unpublished Manuscript, Rochester Institute of Technology, Rochester.
- B. Ghosh and P. De, “Linkage Between Infrastructure and Income Among Indian States: A Tale of Rising Disparity Since Independence,” Indian Journal of Applied Economics, Vol. 8, No. 4, 2000, pp. 391-431.
- K. Kalirajan, “Economic Reform and the Transmission of Growth Impulses across Indian States,” International Journal of Social Economics, Vol. 31, No. 5-6, 2004, pp. 623-636. http://dx.doi.org/10.1108/03068290410529434
- K. Desmetand I. O. Ortin, “Rational under Development,” Scandinavian Journal of Economics, Vol. 109, No. 1, 2007, pp. 1-24. http://dx.doi.org/10.1111/j.1467-9442.2007.00478.x
- S. V. Lall, C. Timmins and S. Yu, “Connecting Lagging and Leading Regions: The Role of Labor Mobility,” Brookings-Wharton Papers on Urban Affairs, 2009, pp. 151-174.
- A. Nocco, “The Rise and Fall of Regional Inequalities With Technological Differences and Knowledge Spillovers,” Regional Science and Urban Economics, Vol. 35, No. 5, 2005, pp. 542-569. http://dx.doi.org/10.1016/j.regsciurbeco.2004.08.001
- J. Sadik, “Technology Adoption, Convergence, and Divergence,” European Economic Review, Vol. 52, No. 2, 2008, pp. 338-355. http://dx.doi.org/10.1016/j.euroecorev.2007.02.005
- F. Castellacci, “Technology Clubs, Technology Gaps, and Growth Trajectories,” Structural Change and Economic Dynamics, Vol. 19, No. 4, 2008, pp. 301-314. http://dx.doi.org/10.1016/j.strueco.2008.07.002
- T. Borota, “Innovation and Imitation in a Model of NorthSouth Trade,” Journal of International Economics, Vol. 87, No. 2, 2012, pp. 365-376. http://dx.doi.org/10.1016/j.jinteco.2012.01.002
- C. I. Jones, “Introduction to Economic Growth,” 2nd Edition, Norton, New York, 2002.
- D. Acemoglu, “Introduction to Modern Economic Growth,” Princeton University Press, Princeton, 2009.
NOTES
1See Jones [10, pp. 20-53] or Acemoglu [2009, pp. 26-76] for comprehensive textbook accounts of the Solow growth model.

