Theoretical Economics Letters
Vol. 3 No. 5A2 (2013) , Article ID: 36454 , 4 pages DOI:10.4236/tel.2013.35A2001
Two-Player Lopsided Contests under Different Timing Assumptions
Department of Economics, Sungkyunkwan University, Seoul, South Korea
Email: khbaik@skku.edu
Copyright © 2013 Kyung Hwan Baik. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 20, 2013; revised August 15, 2013; accepted 21, 2013
Keywords: Contest; Rent Seeking; Timing Assumptions; Underdog; Favorite
ABSTRACT
I study contests in which two asymmetric players compete with each other by expending irreversible efforts to win a prize. I consider three types of games, which are distinguished by their different timing assumptions: the simultaneous-move game, the sequential-move game, and the game with endogenous timing. I compare the outcomes obtained under the different timing assumptions.
1. Introduction
A contest is a situation in which players compete with each other by expending irreversible efforts to win a prize. Examples include rent-seeking contests, patent contests, sporting contests, competition among candidates for office, litigation and tournaments.
The purpose of this paper is to study contests with two asymmetric players under different timing assumptions. The asymmetries between the players arise because of the players’ different valuations for the prize or their different abilities to convert efforts into probability of winning or both. Using the model in Baik [1], I consider three types of games, which are distinguished by their different timing assumptions: the simultaneous-move game, the sequential-move game, and the game with endogenous timing. I compare the outcomes obtained under the different timing assumptions.
This paper is related to Dixit [2], Baik and Shogren [3], Leininger [4], Nitzan [5], Baik [1], Morgan [6], Malueg and Yates [7], and Baik and Lee [8], which study asymmetric contests, with or without endogenous timing.
2. The Model
Two risk-neutral players, 1 and 2, compete with each other by expending their irreversible effort to win a prize. The probability that a player wins the prize is increasing in his own effort level, and decreasing in the rival’s effort level. Player 1 values the prize at  and Player 2 at v, where
and Player 2 at v, where . Each player’s valuation for the prize is positive and publicly known.
. Each player’s valuation for the prize is positive and publicly known.
Let  for
for  represent the effort level expended by player i. Each player’s effort level is positive, and is measured in units commensurate with the prize. Let
represent the effort level expended by player i. Each player’s effort level is positive, and is measured in units commensurate with the prize. Let  denote the probability that player i wins the prize when Players 1 and 2 expend
denote the probability that player i wins the prize when Players 1 and 2 expend  and
and , respectively, where
, respectively, where  and
and 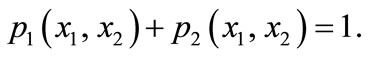 I assume that the contest success function for Player 1 is
I assume that the contest success function for Player 1 is
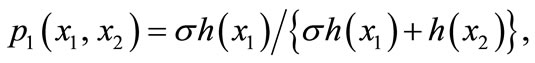 (1)
(1)
where  and the function h has the properties specified in Assumption 1 below. The parameter
and the function h has the properties specified in Assumption 1 below. The parameter  represents the relative abilities of the players to convert effort into probability of winning.
represents the relative abilities of the players to convert effort into probability of winning.
Assumption 1. I assume that , and h is increasing in xi. I assume also that h is twice differentiable, and
, and h is increasing in xi. I assume also that h is twice differentiable, and , where
, where 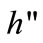 denotes the second partial derivative of the function h.
denotes the second partial derivative of the function h.
It follows from Equation (1) and Assumption 1 that each player’s probability of winning is increasing in his own effort level at a decreasing rate, given a value of  and an effort level of the opponent. It follows also that each player’s probability of winning is decreasing in his opponent’s effort level at a decreasing rate, given a value of
and an effort level of the opponent. It follows also that each player’s probability of winning is decreasing in his opponent’s effort level at a decreasing rate, given a value of  and his own effort level.
and his own effort level.
Let  represents the expected payoff for player i. Then the payoff function for Player 1 is
represents the expected payoff for player i. Then the payoff function for Player 1 is

and that for Player 2 is

I consider three types of games, which are distinguished by their different timing assumptions: the simultaneous-move game, the sequential-move games, and the game with endogenous timing. In the simultaneous-move game, both players choose their effort levels simultaneously, and this order of moves is given exogenously. In a sequential-move game, one player chooses his effort level, and then after observing it, the other player chooses his effort level; this order of moves is given exogenously. In the game with endogenous timing, each player first decides independently whether he will choose his effort level in the first period or in the second period. The players announce their decisions simultaneously. Then, after knowing his opponent’s decision, each player chooses his effort level in the period which he announced.
I assume that all of the above are common knowledge between the players. I employ Nash equilibrium as the solution concept for the simultaneous-move game, and subgame-perfect equilibrium as the solution concept for the sequential-move games and the game with endogenous timing.
3. Preliminaries: Previous Results and Definitions
As proved in Szidarovszky and Okuguchi [9], the simultaneous-move game has a unique pure-strategy Nash equilibrium. Let  denote the Nash equilibrium. Based on the analyses in Baik [1] and Baik and Lee [8], I obtain Lemma 11.
denote the Nash equilibrium. Based on the analyses in Baik [1] and Baik and Lee [8], I obtain Lemma 11.
Lemma 1. a) If  then Player 1’s probability of winning is less than 1/2 at the Nash equilibrium, b) If
then Player 1’s probability of winning is less than 1/2 at the Nash equilibrium, b) If  then Player 1’s probability of winning is greater than 1/2, c) If
then Player 1’s probability of winning is greater than 1/2, c) If 
 then each player’s probability of winning equals 1/2.
then each player’s probability of winning equals 1/2.
In Parts a) and b), the players’ probabilities of winning are not the same at the Nash equilibrium. I call these cases lopsided contests, to which I restrict attention in this paper.
Next, consider the first stage of the game with endogenous timing in which the players decide and announce when to expend their effort. Based on the analyses in Baik and Shogren [3] and Baik and Lee [8], I obtain Lemma 2.
Lemma 2. a) If  then Player 1 announces the first period while Player 2 announces the second period, b) If
then Player 1 announces the first period while Player 2 announces the second period, b) If  then Player 1 announces the second period while Player 2 announces the first period.
then Player 1 announces the second period while Player 2 announces the first period.
Studying two-player contests, Dixit [2] defines the underdog as the player who has a probability of winning less than 1/2, and the favorite as the player who has a probability of winning greater than 1/2, at the Nash equilibrium of a simultaneous-move game. I define the terms, the underdog and the favorite, for each of the three types of games.
Definition 1. a) The simultaneous-move underdog [favorite] is defined as the player who has a probability of winning less [greater] than 1/2, at the Nash equilibrium of the simultaneous-move game. b) The sequential-move underdog [favorite] is defined as the player who has a probability of winning less [greater] than 1/2, in the subgame-perfect equilibrium of a sequential-move game. c) The endogenous-timing underdog [favorite] is defined as the player who has a probability of winning less [greater] than 1/2, in the subgame-perfect equilibrium of the game with endogenous timing.
Using Lemma 1 and Definition 1, I can restate Lemma 2 as follows: In every lopsided contest, the simultaneous-move underdog announces the first period while the simultaneous-move favorite announces the second period. Importantly, this implies that the outcomes—the players’ equilibrium probabilities of winning, effort levels, and expected payoffs—of the game with endogenous timing are exactly the same as those of the sequential-move game with the simultaneous-move underdog as the leader. Consequently, henceforth I restrict attention to just three games: the simultaneous-move game, the sequentialmove game with the simultaneous-move favorite as the leader, and the game with endogenous timing.
4. Comparison of the Three Games
I compare the outcomes—the players’ equilibrium probabilities of winning, effort levels, and expected payoffs— in the three games. Table 1 summarizes the outcomes of the three games, and Propositions 1, 2 and 3 below describe the comparison of these outcomes2. The superscripts SM, SQ, and EN in Table 1 indicate the outcomes of the simultaneous-move game, those of the sequential-move game with the simultaneous-move favorite as the leader, and those of the game with endogenous timing, respectively. I begin by comparing the players’ equilibrium probabilities of winning in the three games.
Proposition 1. In every lopsided contest, the simultaneous-move favorite, the sequential-move favorite, and the endogenous-timing favorite are the same player.
As Table 1 shows, Player 2 is always the favorite regardless of the timing assumption of the contest if

Table 1. Comparison of the outcomes of the three games.
 while Player 1 is so if ασh'
while Player 1 is so if ασh'
 In this contest, the players’ valuations for the prize and their relative abilities determine the players’ strength. A player with less strength tries to overcome his competitive disadvantage given a timing assumption. Unfortunately, however, any timing assumption does not help in putting him in better position.
In this contest, the players’ valuations for the prize and their relative abilities determine the players’ strength. A player with less strength tries to overcome his competitive disadvantage given a timing assumption. Unfortunately, however, any timing assumption does not help in putting him in better position.
Next, I compare the equilibrium effort levels of each player in the three games.
Proposition 2. a) In every lopsided contest, the favorite expends the least effort in the game with endogenous timing, and expends the most effort in the sequentialmove game with the simultaneous-move favorite as the leader. b) In every lopsided contest, the underdog expends the most effort in the simultaneous-move game.
Proposition 2 implies that, in every lopsided contest, each player expends less effort in the game with endogenous timing than in the simultaneous-move game, so that the equilibrium total effort level is less in the game with endogenous timing than in the simultaneous-move game3. Proposition 2 can be explained as follows. In the sequential-move game with the simultaneous-move favorite as the leader, the favorite expends more effort than in the simultaneous-move game to preempt the opponent with less strength. In response to this preemptive behavior, the simultaneous-move underdog steps back by expending less effort than in the simultaneous-move game. On the other hand, in the game with endogenous timing (or, equivalently, in the sequential-move game with the simultaneous-move underdog as the leader), the underdog expends less effort than in the simultaneous-move game to avoid a big fight against the opponent with more strength. This in turn allows the simultaneous-move favorite to ease up and expend less effort than in the simultaneous-move game.
Finally, I compare the equilibrium expected payoffs of each player in the three games.
Proposition 3. a) In every lopsided contest, the favorite has the least expected payoff in the simultaneousmove game. b) In every lopsided contest, the underdog has the most expected payoff in the game with endogenous timing, and has the least expected payoff in the sequential-move game with the simultaneous-move favorite as the leader.
Proposition 3 implies that, in every lopsided contest, each player’s equilibrium expected payoff is greater in the game with endogenous timing than in the simultaneous-move game, so that the sum of the players’ equilibrium expected payoffs is greater in the game with endogenous timing than in the simultaneous-move game. The intuition behind Proposition 3 is as follows. In the sequential-move game with the simultaneous-move favorite as the leader, the favorite earns more expected payoff, due to the first-mover advantage, than in the simultaneous-move game, whereas the simultaneous-move underdog earns less expected payoff, due to the second-mover disadvantage, than in the simultaneous-move game. On the other hand, in the game with endogenous timing (or, equivalently, in the sequential-move game with the simultaneous-move underdog as the leader), both the simultaneous-move favorite and the underdog engage in less competition, and thus end up with greater equilibrium expected payoffs, than in the simultaneous-move game.
5. Conclusion
I have studied contests in which two asymmetric players compete with each other by expending irreversible efforts to win a prize. I have compared the outcomes in the three games: the simultaneous-move game, the sequential-move game with the simultaneous-move favorite as the leader, and the game with endogenous timing. I have found that, in every lopsided contest, the same player becomes the favorite across the three games. However, I have found that, in every lopsided contest, the equilibrium effort levels of each player differ across the three games; the equilibrium expected payoffs of each player differ across the three games.
REFERENCES
- K. H. Baik, “Effort Levels in Contests with Two Asymmetric Players,” Southern Economic Journal, Vol. 61, No. 2, 1994, pp. 367-378. doi:10.2307/1059984
- A. Dixit, “Strategic Behavior in Contests,” American Economic Review, Vol. 77, No. 5, 1987, pp. 891-898.
- K. H. Baik and J. F. Shogren, “Strategic Behavior in Contests: Comment,” American Economic Review, Vol. 82, No. 1, 1992, pp. 359-362.
- W. Leininger, “More Efficient Rent-Seeking—A Münchhausen Solution,” Public Choice, Vol. 75, No. 1, 1993, pp. 43-62. doi:10.1007/BF01053880
- S. Nitzan, “More on More Efficient Rent Seeking and Strategic Behavior in Contests: Comment,” Public Choice, Vol. 79, Nos. 3-4, 1994, pp. 355-356. doi:10.1007/BF01047778
- J. Morgan, “Sequential Contests,” Public Choice, Vol. 116, Nos. 1-2, 2003, pp. 1-18. doi:10.1023/A:1024252514806
- D. A. Malueg and A. J. Yates, “Equilibria and Comparative Statics in Two-Player Contests,” European Journal of Political Economy, Vol. 21, No. 3, 2005, pp. 738-752. doi:10.1016/j.ejpoleco.2004.11.004
- K. H. Baik and J. H. Lee, “Endogenous Timing in Contests with Delegation,” Economic Inquiry. In press. doi:10.1111/j.1465-7295.2012.00487.x
- F. Szidarovszky and K. Okuguchi, “On the Existence and Uniqueness of Pure Nash Equilibrium in Rent-Seeking Games,” Games and Economic Behavior, Vol. 18, No. 1, 1997, pp. 135-140. doi:10.1006/game.1997.0517
NOTES
1For concise exposition, I do not provide the proofs of the lemmas and propositions presented in Sections 3 and 4. They are available from the author upon request. For the proof of Lemma 2, see also Leininger [4].
2If  then I have
then I have  for i =
for i =  so that I have
so that I have 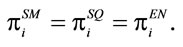
3Baik and Shogren [3], Leininger [4], Nitzan [5] and Baik [1] obtain this result.

