Theoretical Economics Letters
Vol. 3 No. 5A1 (2013) , Article ID: 36254 , 5 pages DOI:10.4236/tel.2013.35A1001
Ship Inspections in Invasive Species Management: Alternate Regimes and Their Properties
1Department of Economics, Rochester Institute of Technology, Rochester, USA
2Department of Economics, University of Texas at San Antonio, San Antonio, USA
Email: aabgsh@rit.edu, Hamid.Beladi@utsa.edu
Copyright © 2013 Amitrajeet A. Batabyal, Hamid Beladi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 13, 2013; revised July 13, 2013; accepted August 13, 2013
Keywords: Inspection; Invasive Species; Management; Performance Measure; Uncertainty
ABSTRACT
When it comes to inspections in invasive species management, the literature has shown that there is frequently a tension between economic cost reduction and inspection stringency. As such, we analyze the properties of two probabilistic inspection regimes that are designed to screen arriving ships in a seaport for the presence of one or more deleterious invasive species. In the first regime, the seaport inspector screens arriving ships by using fast (less stringent) and slow (more stringent) protocols. In the second regime, the inspector uses a uniformly stringent protocol with stages. We use the theory of continuous time Markov chains (CTMCs) to delineate both inspection regimes. Next, we derive some key long run performance measures associated with each of these two regimes. Finally, we discuss the implications of our analysis for practical invasive species management.
1. Introduction
In addition to cargo, ships frequently carry a whole host of invasive—also known as alien, exotic, or non-native—animal and plant species from one part of the world to another. There are many ways in which ships carry invasive animal and plant species from one region of the world to another. For instance, marine invasive species have been introduced accidentally into a region by ships dumping their ballast water. Cargo ships commonly carry ballast water in order to enhance vessel stability when they are not carrying full loads. When these ships come into a seaport, this ballast water must be released before cargo can be loaded. This means of invasive species introductions is salient and Yang and Perakis [1], Batabyal et al. [2], and Batabyal and Beladi [3] have now studied the problem of managing invasive species that have been introduced into a particular region by means of the jettisoning of ballast water.
Containers are commonly used on ships to carry cargo from one nation to another and these containers are frequently the source for the unintentional introduction of one or more invasive species. Such introductions take place because invasive species can remain hidden in containers for long periods of time. In addition, substances such as wood—often used to pack cargo in containers—may themselves contain invasive species. In this regard, Batabyal and Nijkamp [4] note that a joint report from the United States Department of Agriculture (USDA), the Animal and Plant Health Inspection Service (APHIS), and the United States Forest Service (USFS) shows that nearly 51.8% of maritime shipments contain solid wood packing substances and that infection rates for solid wood packing substances are substantial. This same report goes on to state that inspections of wooden spools from China revealed infection rates between 22% and 24% and inspections of braces for granite blocks imported into Canada were found to hold live insects 32% of the time [5, pp. 27-28].
From the standpoint of a manager in a seaport, there are a number of actions that this individual can take to address the problem of biological invasions. These actions are typically pre-invasion or post-invasion in nature. The objective of pre-invasion actions is to prevent invasive species from invading a new habitat. In contrast, post-invasion actions involve the optimal control of an invasive species, given that this species has already invaded a new habitat. Inspections are a basic pre-invasion tool that is available to managers interested in precluding biological invasions. They are routinely used in seaports—and in airports and land border crossings as well—to screen the container cargo on arriving ships in a seaport. Given the significance of inspections, several researchers have now formally studied inspections in the context of invasive species management.
McAusland and Costello [6] show that when one takes an intertemporal view and considers the future effects of current species introductions, one is naturally led to favor more stringent inspections. Ameden et al. [7] study border enforcement and firm responses in a theoretical model of invasive species management. They demonstrate that increased inspections are likely to result in a decrease of both shipments and due care by importers. Batabyal and Yoo [8] analyze a random inspection scheme and compute the average total fines that will be collected by an inspector who uses this scheme to screen arriving ships for the presence of one or more invasive species.
Batabyal [9] studies inspections in a scenario in which a seaport inspector places equal weight on biological invasion damage control and on economic cost reduction. In particular, he notes that the optimal dependability and speed of inspections is the solution to a particular long run expected net cost (LRENC) minimization problem. Merel and Carter [10] show that the import risk from invasive species is usefully handled with inspections. Specifically, when inspection costs are relatively low, a penalty on contaminated imports is likely to be superior to a simple tariff designed to diminish the overall volume of trade. Sanchirico et al. [11] point to the ways in which inspections are useful in managing invasive species when these inspections are a single policy tool in a package consisting of other policy tools as well.
The three studies that are closest to the present paper are De Angelo et al. [12,13] and Batabyal [14]. De Angelo et al. [12,13] concentrate on the twin objectives of reducing the economic cost associated with inspections and on diminishing the likelihood of one or more biological invasions. These authors contend that an inspector who places a relatively large (small) weight on invasion damage control will, ceteris paribus, want to inspect ships more (less) stringently. Batabyal [14] studies the behavior of a risk loving inspector who is more concerned about reducing the economic cost associated with inspections than he is about biological invasion damage control.
We depart from the studies discussed above and analyze inspections in invasive species management in a completely different way. Specifically, we analyze the properties of two probabilistic inspection regimes that are designed to screen arriving ships in a stylized seaport for the presence of one or more detrimental invasive species. In the first or the fast-slow inspection regime, the seaport inspector screens arriving ships by using a fast (less stringent) and a slow (more stringent) protocol. In the second or the uniform inspection regime, the inspector uses a uniformly stringent protocol with stages. We use the theory of continuous time Markov chains (CTMCs)1 to delineate both inspection regimes. Next, we derive some key long run performance measures associated with each of these two inspection regimes. Finally, we discuss the implications of our analysis for practical invasive species management.
The rest of this paper is organized as follows. Section 2 first uses the theory of CTMCs to provide a detailed description of the fast-slow inspection regime. Next, this Section computes three long run performance measures for this inspection regime and then discusses their practical relevance. Similarly, Section 3 first uses the theory of CTMCs to provide a detailed delineation of the uniform inspection regime with stages. Next, this Section calculates four long run performance metrics for this inspection regime and then comments on their practical usefulness. Section 4 concludes and then offers suggestions for future research on the subject of this paper.
2. The Fast-Slow Inspection Regime
2.1. Preliminaries
Ships carrying container cargo arrive at the seaport in a particular geographical region of a nation in accordance with a stationary Poisson process with time independent rate λ > 0. The inspector in charge of conducting inspections of arriving ships in this seaport has access to fast (less stringent) and slow (more stringent) inspection protocols. An arriving ship that finds both protocols in use is “rejected” in the sense that it cannot be inspected right away but must wait in a queue.
The seaport inspector has hierarchical preferences as far as the temporal stringency of inspections is concerned. Specifically, what this means is that unless both inspection protocols are in use, the fast protocol is assigned to an arriving ship. The slow protocol is assigned to an arriving ship only when the fast protocol is unavailable. The time it takes to complete the inspection of a ship with the fast (slow) protocol is exponentially distributed with positive mean 1/β1 (1/β2). It is not possible for our inspector to switch between the fast and the slow inspection protocols.
To proceed further, let Z(t) denote the state of the fast-slow inspection regime at any time t. As far as the state space of Z(t) is concerned, there are four cases to consider. We shall say that the inspection regime is in state (0,0) if the fast and the slow protocols are both not in use. We shall say that the regime is in state (1,0) if the fast protocol is in use but the slow protocol is not. We shall say that the regime is in state (0,1) if the slow protocol is in use but the fast protocol is not. Finally, we shall say that the regime is in state (1,1) if both fast and slow protocols are in use. Now, from our model, the state space specification, and the discussion in Tijms [16] it follows that the stochastic process {Z(t)} is a CTMC. Our next task is to compute three long run, i.e., as time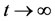 , performance measures for this CTMC model of the fast-slow inspection regime.
, performance measures for this CTMC model of the fast-slow inspection regime.
2.2. Three Performance Measures
We begin by specifying the so called equilibrium probabilities2. To this end, let p(i,j) be the equilibrium probability of state (i,j). Then, the relevant equilibrium equations for our CTMC model of the fast-slow inspection regime are given by
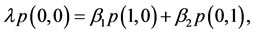 (1)
(1)
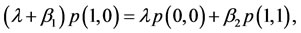 (2)
(2)
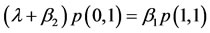 (3)
(3)
and
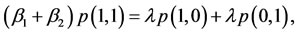 (4)
(4)
with the normalizing equation
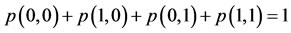 (5)
(5)
With Equations (1)-(5) in place, we are now in a position to compute the three performance measures for the fast-slow inspection regime.
The first two performance measures that we are interested in calculating concern the long run fraction of time that the fast and the slow inspection protocols are used. To undertake this calculation, recall the description of the four states in the last paragraph of Section 2.1. For the fast protocol, the states of interest are (1,0) and (1,1). Now, using the equilibrium probabilities specified in Equations (1)-(5) above and the properties of CTMCs3, we deduce that the long run fraction of time our seaport inspector uses the fast protocol is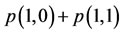 . Moving to the slow protocol, the relevant states of interest now are (0,1) and (1,1). Once again, using the equilibrium probabilities, the long run fraction of time our seaport inspector uses the slow protocol is given by
. Moving to the slow protocol, the relevant states of interest now are (0,1) and (1,1). Once again, using the equilibrium probabilities, the long run fraction of time our seaport inspector uses the slow protocol is given by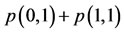 .
.
Recall from Section 2.1 that an arriving ship in the seaport under study that finds both protocols in use is “rejected” in the sense that it cannot be inspected right away but must wait in a queue. As such, it is of considerable interest to determine the long run fraction of all ships that cannot be inspected upon arrival but must wait to be inspected. To compute this fraction, we shall use the “Poisson arrivals see time averages” or PASTA property4. This property tells us that the long run fraction of time a stochastic system is in a particular state is equal to the long run fraction of arriving ships that find the stochastic system in this same state. The state of interest is (1,1). A simple application of the PASTA property now tells us that the long run fraction of all ships that are “rejected” and hence must wait is equal to the equilibrium probability p(1,1).
The three performance measures computed in the preceding two paragraphs can help our seaport inspector conduct the inspection function in conformity with his hierarchical preferences. For instance, as in Batabyal [14], suppose that our seaport manager is more concerned about reducing the economic cost associated with inspections than he is about biological invasion damage control. Then, he will want to dispense with inspections relatively quickly and this, in turn, means that he will choose 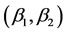 to increase the fraction of time that the fast inspection protocol is used. Put differently, he will raise the sum
to increase the fraction of time that the fast inspection protocol is used. Put differently, he will raise the sum 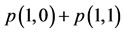 In contrast, relative to economic cost reduction, if this individual is more worried about one or more biological invasions then he will attempt to conduct inspections relatively slowly. This means that he will attempt to select
In contrast, relative to economic cost reduction, if this individual is more worried about one or more biological invasions then he will attempt to conduct inspections relatively slowly. This means that he will attempt to select 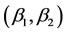 to increase the fraction of time that the slow inspection protocol is used. Finally, the equilibrium probability p(1,1) provides our seaport inspector with a measure of the efficiency with which he is conducting his screening duties. We now proceed to discuss the uniform inspection regime.
to increase the fraction of time that the slow inspection protocol is used. Finally, the equilibrium probability p(1,1) provides our seaport inspector with a measure of the efficiency with which he is conducting his screening duties. We now proceed to discuss the uniform inspection regime.
3. The Uniform Inspection Regime
3.1. Preliminaries
As in Section 2.1, once again ships carrying container cargo arrive at the seaport under study in accordance with a stationary Poisson process with time invariant rate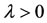 . However, this time, our seaport inspector uses a uniform protocol with stages to screen arriving ships. The time it takes to complete inspections is exponentially distributed with positive mean
. However, this time, our seaport inspector uses a uniform protocol with stages to screen arriving ships. The time it takes to complete inspections is exponentially distributed with positive mean 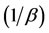 and only one ship can go through an inspection stage at any point in time.
and only one ship can go through an inspection stage at any point in time.
The matter of the “rejection” of ships discussed in Section 2.1 is now handled a little differently. The seaport inspector now uses the following access control rule to determine when a ship is allowed in the seaport immediately for inspection. Specifically, a newly arriving ship is accepted for inspection as long as less than U other ships are present in the uniform inspection protocol with stages. As soon as the number of ships in the inspection protocol has dropped to u, newly arriving ships are again admitted into the uniform inspection protocol. The nonnegative integers (u,U) are given to the seaport inspector and we suppose that 0 ≤ u < U holds.
To proceed further, let Z1(t) denote the number of ships in the seaport under study at any time t. Let Z2(t) equal 1 if the seaport inspector’s uniform protocol is accepting new ships for inspection and let Z2(t) equal 0 otherwise. We are interested in the stochastic process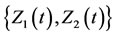 . Now, from our model stipulation thus far and from the commentary in Tijms [16] it follows that the stochastic process
. Now, from our model stipulation thus far and from the commentary in Tijms [16] it follows that the stochastic process 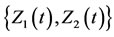 is a CTMC with state space given by
is a CTMC with state space given by
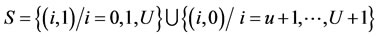 (6)
(6)
Our next task is to compute four performance metrics for this CTMC model of the uniform inspection regime.
3.2. Four Performance Metrics
As in Section 2.2, we begin with the equilibrium probabilities. Let p(i,j) denote the equilibrium probability of state (i,j). These equilibrium probabilities are obtained using the flow rate equation method. This method involves equating the rate out of state (i,j) to the rate into state (i,j).5 Our first performance metric is the long run fraction of time the uniform inspection protocol is idle. The reader will note that this fraction is given by the equilibrium probability p(0,1).
Consistent with the third performance measure computed in Section 2.2, the second performance metric we are interested in calculating now is the long run fraction of all arriving ships in our seaport that are “rejected” in the sense that they are not inspected right away. To calculate this fraction, we shall use the state space given in Equation (6) and the previously described PASTA property. Because Poisson arrivals see time averages, we infer that the long run fraction of all arriving ships that are rejected is given by
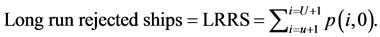 (7)
(7)
The third performance metric we are interested in calculating is the long run average number of ships that are waiting to be inspected in the seaport under study. The key point to understand now is that this third performance metric is identical to the long run number of customers in a queue at time t as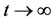 . In the queuing theory literature6, this metric is often denoted by Lq. To determine Lq in our case, we will need to weight the equilibrium probabilities p(i,1) and p(i,0) in an appropriate manner and then sum the resulting expression. Once again, keeping the state space described by Equation (6) in mind, we obtain the metric we seek. Specifically, we get
. In the queuing theory literature6, this metric is often denoted by Lq. To determine Lq in our case, we will need to weight the equilibrium probabilities p(i,1) and p(i,0) in an appropriate manner and then sum the resulting expression. Once again, keeping the state space described by Equation (6) in mind, we obtain the metric we seek. Specifically, we get
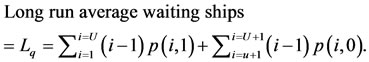 (8)
(8)
The fourth and final performance metric we are interested in calculating is the long run average delay in queue per ship that has been accepted for inspection. As in the computation of the third performance metric, once again, we use a queuing theoretic relationship. In this case, the salient point to note is that the fourth performance metric we seek is the same as the long run average delay in queue per customer. In the queuing theory literature, this delay is frequently denoted by Wq. Now, adapting equation 2.3.1 in Tijms [16, p. 51] to our problem, it is clear that the long run average delay in queue per ship that has been accepted for inspection or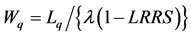 . Making the appropriate substitutions from Equations (7) and (8), we get
. Making the appropriate substitutions from Equations (7) and (8), we get
 (9)
(9)
From the standpoint of practical invasive species management, the four performance metrics computed in this Section can help our seaport inspector in three key ways. First, our seaport manager can choose one or more of the quantities 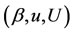 to optimize the performance metrics we have derived thus far in this Section. In this regard, the long run fraction of all arriving ships that are rejected (Equation (7)) and the long run average delay in queue per ship that has been accepted for inspection (Equation (9)) are likely to be key performance metrics that our seaport inspector would like to minimize. Our analysis shows that this inspector can, inter alia, choose U to minimize either Equation (7) or (9).
to optimize the performance metrics we have derived thus far in this Section. In this regard, the long run fraction of all arriving ships that are rejected (Equation (7)) and the long run average delay in queue per ship that has been accepted for inspection (Equation (9)) are likely to be key performance metrics that our seaport inspector would like to minimize. Our analysis shows that this inspector can, inter alia, choose U to minimize either Equation (7) or (9).
Second and more generally, our seaport manager can use one or more of the four performance metrics we have derived to set up and maximize a net social benefit from inspections objective function. In this case, one or more of the four performance metrics derived in this Section would make up the more general net social benefit criterion function and the choice variables would be one or more of the quantities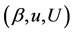 .
.
Finally, instead of using one or more of the four performance metrics directly for the purpose of optimization, the seaport manager can also solve a constrained optimization problem where one or more of this Section’s performance metrics enters the optimization problem as a constraint. In this way of looking at the screening function, the seaport inspector would attempt to ensure that the expression in Equation (9), for instance, is no bigger than some acceptable upper bound or threshold. This completes our discussion of the properties of two probabilistic inspection regimes in the context of invasive species management.
4. Conclusions
In this paper, we analyzed the properties of two probabilistic inspection regimes that were designed to screen arriving ships in a seaport for the presence of one or more deleterious invasive species. In the first regime, the seaport inspector screened arriving ships by using a fast (less stringent) and a slow (more stringent) protocol. In the second regime, the inspector used a uniformly stringent protocol with stages. We used the theory of CTMCs to describe the two inspection regimes. Next, we derived some key long run performance measures associated with each of these two inspection regimes. Finally, we discussed in detail the implications of our analysis for practical invasive species management.
The analysis in this paper can be extended in a number of directions. Here are two possible extensions. First, to account for the fact that ships are more likely to arrive at the seaport under study at certain times than at others, one could model the ship arrival process with a non-stationary Poisson process with a time dependent intensity function given by, for instance,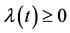 . Second, from the vantage point of the efficient allocation of inspection resources, it would be useful to set up—possibly with one or more constraints—and then solve an optimization problem of the sort discussed towards the end of Section 3.2. Research on inspections as a tool for managing deleterious invasive species that incorporate these aspects of the problem into the analysis will provide additional insights into a management problem that has considerable economic and ecological ramifications.
. Second, from the vantage point of the efficient allocation of inspection resources, it would be useful to set up—possibly with one or more constraints—and then solve an optimization problem of the sort discussed towards the end of Section 3.2. Research on inspections as a tool for managing deleterious invasive species that incorporate these aspects of the problem into the analysis will provide additional insights into a management problem that has considerable economic and ecological ramifications.
5. Acknowledgements
Batabyal acknowledges financial support from the Gosnell endowment at RIT and he thanks Cass Shellman for help in formatting the paper.
REFERENCES
- Z. Yang and A. N. Perakis, “Multiattribute Decision Analysis of Mandatory Ballast Water Treatment Measures in the US Great Lakes,” Transportation Research Part D, Vol. 9, No. 1, 2004, pp. 81-86.
- A. A. Batabyal, H. Beladi and W. W. Koo, “Maritime Trade, Biological Invasions, and the Properties of Alternate Inspection Regimes,” Stochastic Environmental Research and Risk Assessment, Vol. 19, No. 3, 2005, pp. 184-190. doi:10.1007/s00477-004-0216-2
- A. A. Batabyal and H. Beladi, “International Trade and Biological Invasions: A Queuing Theoretic Analysis of the Prevention Problem,” European Journal of Operational Research, Vol. 170, No. 3, 2006, pp. 758-770. doi:10.1016/j.ejor.2004.07.065
- A. A. Batabyal and P. Nijkamp, “On Container Versus Time Based Inspection Policies in Invasive Species Management,” Stochastic Environmental Research and Risk Assessment, Vol. 19, No. 5, 2005, pp. 340-347. doi:10.1007/s00477-005-0239-3
- USDA, APHIS and USFS, “Pest Risk Assessment for Importation of Solid Wood Packing Materials into the United States,” 2000. http://www.aphis.usda.gov/ppq/pra/swpm/complete.pdf
- C. McAusland and C. Costello, “Avoiding Invasives: Trade-Related Policies for Controlling Unintentional Exotic Species Introductions,” Journal of Environmental Economics and Management, Vol. 48, No. 2, 2004, pp. 954- 977. doi:10.1016/j.jeem.2003.11.002
- H. A. Ameden, S. B. Cash and D. Zilberman, “Border Enforcement and Firm Response in the Management of Invasive Species,” Journal of Agricultural and Applied Economics, Vol. 39, 2007, pp. 35-46.
- A. A. Batabyal and S. J. Yoo, “A Theoretical Analysis of Random Inspections and Fines in Invasive Species Management,” Economics Bulletin, Vol. 17, No. 15, 2008, pp. 1-9.
- A. A. Batabyal, “A Theoretical Note on the Optimal Dependability and Speed of Container Inspections in Invasive Species Management,” Studies in Regional Science, Vol. 38, No. 1, 2008, pp. 199-204. doi:10.2457/srs.38.199
- P. R. Merel and C. A. Carter, “A Second Look At Managing Import Risk from Invasive Species,” Journal of Environmental Economics and Management, Vol. 56, No. 3, 2008, pp. 286-290. doi:10.1016/j.jeem.2008.02.002
- J. N. Sanchirico, H. J. Albers, C. Fischer and C. Coleman. “Spatial Management of Invasive Species: Pathways and Policy Options,” Environmental and Resource Economics, Vol. 45, No. 4, 2010, pp. 517-535. doi:10.1007/s10640-009-9326-0
- G. J. DeAngelo, A. A. Batabyal and S. Kumar, “On Economic Cost Minimization Versus Biological Invasion Damage Control,” In: A. Oude Lansink, Ed., New Approaches to the Economics of Plant Health, Springer-Verlag, Heidelberg, 2006, pp. 23-37.
- G. J. DeAngelo, A. A. Batabyal and S. Kumar, “An Analysis of Economic Cost Minimization and Biological Invasion Damage Control Using the AWQ Criterion,” Annals of Regional Science, Vol. 41, No. 3, 2007, pp. 639- 655. doi:10.1007/s00168-007-0121-y
- A. A. Batabyal, “An Analysis of Inspections When Economic Cost Reduction Matters More than Biological Invasion Damage Control,” In: A. A. Batabyal, Dynamic and Stochastic Resource Economics, World Scientific Publishing, Forthcoming.
- S. M. Ross, “Stochastic Processes,” 2nd Edition, Wiley, New York, 1996.
- H. C. Tijms, “A First Course in Stochastic Models,” Wiley, Chichester, 2003. doi:10.1002/047001363X
NOTES
1See Ross [15, pp. 231-294] or Tijms [16, pp. 141-186] for textbook expositions of continuous time Markov chains (CTMCs).
2See Tijms [16, pp. 149-153] for a textbook account of these probabilities.
3See Tijms [16, pp. 147-157] for additional details.
4See Tijms [16, pp. 53-58] for a textbook treatment of the PASTA property.
5See Ross [15, pp. 251-257] or Tijms [14, pp. 147-154] for textbook discussions of this method.
6See Tijms [16, pp. 50-53] for additional details on this point and on the prominent formula of Little.

