Theoretical Economics Letters
Vol. 3 No. 3A (2013) , Article ID: 32964 , 6 pages DOI:10.4236/tel.2013.33A001
A Model of Progressive Employee Compensation and Superstardom
School of Management, State University of New York at Buffalo, Buffalo, USA
Email: {mgthamle}@buffalo.edu
Copyright © 2013 Susan Hamlen et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 24, 2013; revised March 24, 2013; accepted April 24, 2013
Keywords: Progressive Salaries; Managers; Superstardom
ABSTRACT
This paper identifies the condition leading to a progressive salary situation wherein the elasticity of compensation with respect to ability is greater than unity, i.e., a small percentage advantage in ability results in a disproportional increase in compensation. This analysis also helps explain the “superstar phenomenon” made famous by Rosen (1981). Two assumptions are made. The first is that there is a generalized Cobb-Douglas type of production function wherein different hierarchies of employees of different abilities are viewed as distinct inputs. The second is that the distribution of ability is bell-shaped or approximately normally distributed, and can be approximated by a Poisson distribution. The model is applied using average outgoing salaries of MBA students from different universities compared to their average test scores.
1. Introduction
Our primary goal is to analyze the combined supply and demand factors that determine the elasticity of employee compensation relative to ability, where ability is assumed to be bell-shaped or normally distributed. Although the results are applicable to any occupation, we use the market for new managers as a relevant example. We attribute this application to early work by Rosen [1], who was interested in the progressive nature of managers’ salaries. Rosen [2] also introduced the “superstar phenomenon”, which seeks to explain why the top performers in many fields of endeavor, e.g., sports and music, receive compensation that is highly elastic with respect to ability. Progressive salary structures in the upper tail of the distribution of ability tend to result in highly skewed incomes in favor of the few most able managers. This, in turn, can cause social and political discontent.
In the second section below we present a brief overview of the relevant literature. The third section introduces the Cobb-Douglas style production function assumed in the analysis. It, in turn, is used to generate demand functions for employees of any ability level. The fourth section identifies distributional assumptions concerning ability over the population of competing employees. The discrete Poisson distribution is used for mathematical convenience since it can be used to approximate a continuous normal distribution, and yields results that are easier to derive than those obtained by assuming a continuous distribution. The Poisson distribution of ability is combined with the demand functions from the third section to produce the final condition under which the progressive salary will exist. The fifth section applies the result to the relationship between average potential ability of graduating MBA (Master of Business Administration) students and their average outgoing salaries. As predicted by the model, the elasticity of compensation is greater than unity at higher levels of ability and less than unity at lower levels of ability. The sixth section summarizes our conclusions.
2. Literature Review
Rosen [1] was one of the first to become interested in the progressive nature of salaries. In particular he was interested in compensation to managers. He determined that there are distinct hierarchies of managers. At each higher level or hierarchy, the effects of managers’ decisions are passed down to all subdivisions, causing multiple effects. Thus incremental efforts by upper management can engender higher returns than incremental efforts made by lower hierarchies of management. This implies that, for any given level of employment, the demand curve for higher hierarchy managers will be above that for lower hierarchy managers. From a modeling perspective, having a distinct set of hierarchical positions implies that we cannot treat management as a single class of homogeneous managers. Each level of the hierarchy must be viewed as a distinct factor of production. This also implies that there is a matching mechanism that efficiently allocates talent to the appropriate hierarchy.
The superstar phenomenon was defined by Rosen [2] as the situation where “small differences in talent become magnified into larger earnings differences, with great magnification if the earnings-talent gradient increases sharply near the top of the scale” (p. 846). He motivated the theory by describing how Alfred Marshall [3] was concerned with the distributional effects of a progressive salary structure with respect to ability, particularly at the upper tail of the distribution for ability. The superstar concept has been applied to various economic situations in the entertainment industry, e.g., Scully [4], Jones and Walsh [5], Hamlen [6,7], Chung and Cox [8] and Lucifora and Simmons [9].
Murphy, Shleifer, and Vishny [10] (MSV) introduce a model of superstardom in the market for managers. They examine the situation where there are basically two hierarchies of management: one where less able managers receive a salary or wage based on standard marginal productivity conditions, and another where more able managers receive compensation based on some portion of the firm’s profits. They show that, in progressing from the lower management hierarchy to the higher management hierarchy, compensation can increase to an extent that is more than proportional to the manager’s differences in ability. Thus they considered this outcome an example of the “superstar phenomenon”. The MSV model provides a rationale for superstardom in the market for managers, but, as shown in this paper, the same phenomenon exists even if there is no hierarchy that receives a portion of the profits.
3. Production and Demand for Employees
We begin with an aggregate production function, written as a generalized Cobb-Douglas type production function.
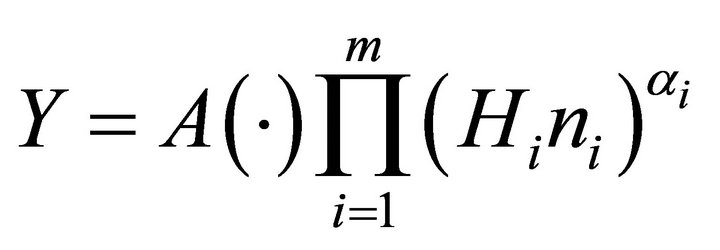 (1)
(1)
In Equation (1), the output, Y, is the real GDP. The parameter “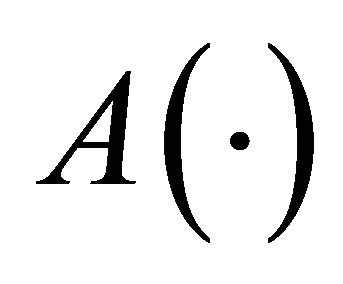 ” incorporates both the state of technology and all inputs not under study, e.g., physical capital stock. The coefficients
” incorporates both the state of technology and all inputs not under study, e.g., physical capital stock. The coefficients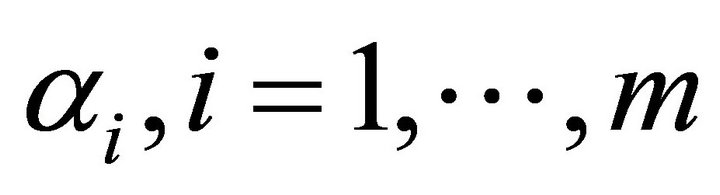 , are the elasticities of output relative to the increases in human capital stock,
, are the elasticities of output relative to the increases in human capital stock, 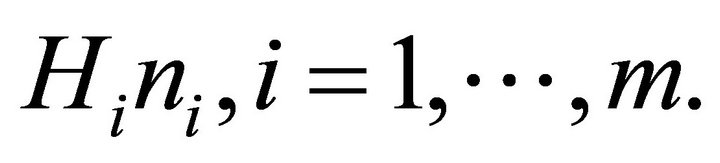 These coefficients will be referred to as the production elasticities in order to distinguish these from the elasticities of salary or wage relative to a measure of ability, which is the primary interest of this paper.
These coefficients will be referred to as the production elasticities in order to distinguish these from the elasticities of salary or wage relative to a measure of ability, which is the primary interest of this paper.
Assume there are m distinct hierarchies of employees.
In the hierarchical system described by Rosen these different hierarchies are treated as separate factors of production. Individuals seek employment in the highest hierarchy for which they may be considered, and the hiring agents for each hierarchy seek the potentially most able employees that are available. The variable Hi is a common measure of the ability associated with individuals currently hired in hierarchy i, and ni is the number of such individuals employed in that hierarchy. It must be emphasized that each ni consists of the stock of existing managers suited for that hierarchy. New additions to each hierarchy are relatively small in number relative to the existing stock of such employees. They accept the going wage rate for that hierarchy set by the supply and demand in the larger market of existing employees. This is basically the same as the assumption made in Witte’s [11] classic model for physical capital stock, where the larger market for existing capital stock determines the compensation rate in the smaller market for new capital stock.
We assume for convenience that the hierarchies of employees in Equation (1) are arranged from the lowest hierarchy, ![]() , to the highest level,
, to the highest level,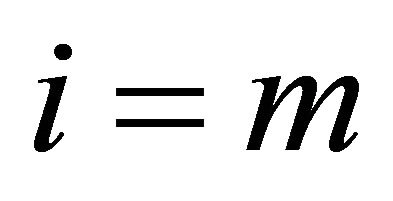 . The product Hini becomes an approximate measure of the total amount of human capital stock currently used in the ith hierarchy. We assume that as ai approaches a continuum of hierarchies from
. The product Hini becomes an approximate measure of the total amount of human capital stock currently used in the ith hierarchy. We assume that as ai approaches a continuum of hierarchies from ![]() to m, the difference between each ai and ai+1 becomes small, even though the difference between a1 and am may be quite significant.
to m, the difference between each ai and ai+1 becomes small, even though the difference between a1 and am may be quite significant.
Next, we make the usual assumption on employee hiring, that the salary of each individual in hierarchy i is based on the standard competitive model of optimal hiring within that hierarchy. The salary to the ith hierarchy employee is equal to the value of the marginal product of the last individual hired in that hierarchy, or:
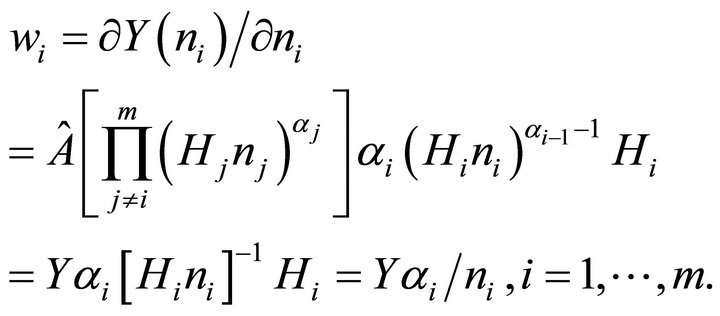 (2)
(2)
In Equation (2) the term  implies that the other inputs are assumed to be at their optimal values. In the final form of Equation (2), members of hierarchy
implies that the other inputs are assumed to be at their optimal values. In the final form of Equation (2), members of hierarchy 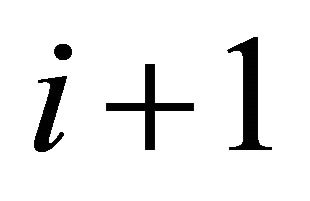 receive a higher salary than those of hierarchy i if
receive a higher salary than those of hierarchy i if 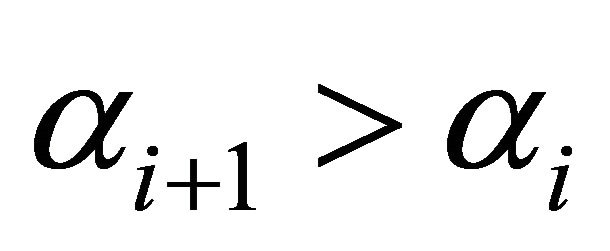 or
or 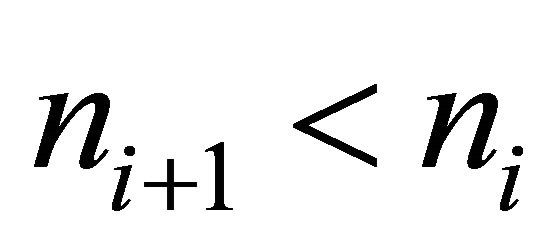 or some combination of both. In other words higher wages go to the employees in higher hierarchies if they have a higher production elasticity of output with respect to number of employees hired or if there are less individuals qualified to be employed in the higher hierarchy. The components
or some combination of both. In other words higher wages go to the employees in higher hierarchies if they have a higher production elasticity of output with respect to number of employees hired or if there are less individuals qualified to be employed in the higher hierarchy. The components 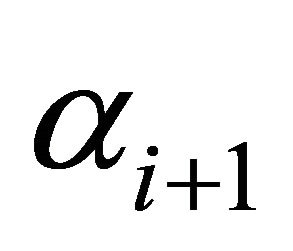 and
and 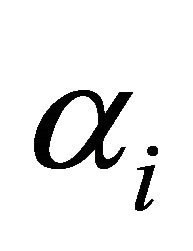 are demand-side conditions for hiring in the respective hierarchy while the components
are demand-side conditions for hiring in the respective hierarchy while the components 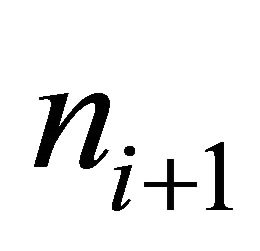 and
and 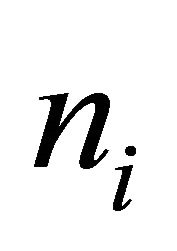 are supply-side conditions. It is useful to note that from Equation (2) the ratio
are supply-side conditions. It is useful to note that from Equation (2) the ratio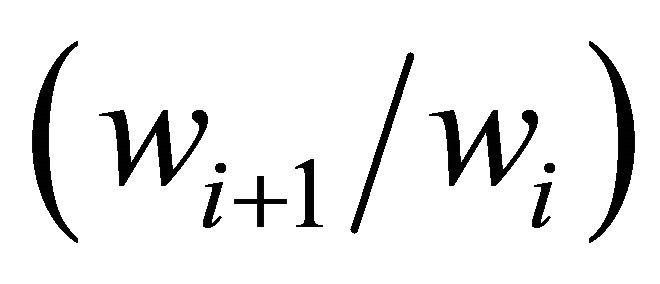 , evaluated at
, evaluated at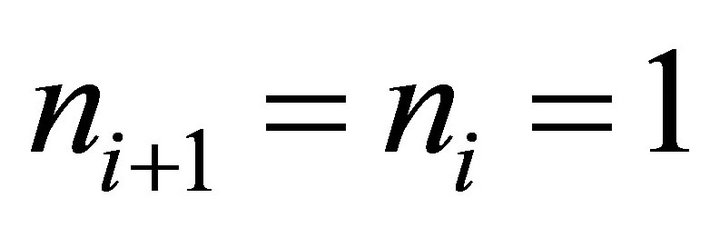 , i.e., the first person hired, yields
, i.e., the first person hired, yields
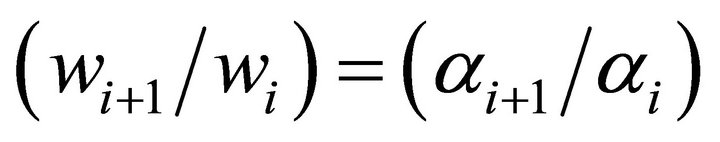 . Thus the ratio
. Thus the ratio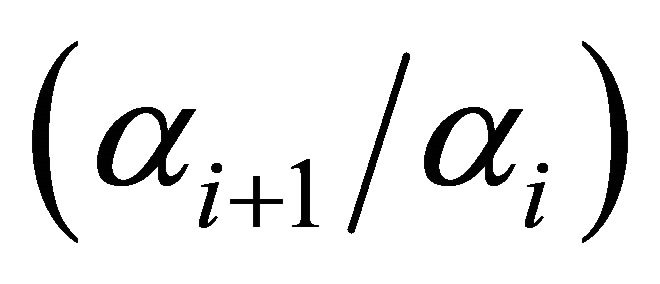 , which appears throughout the paper, represents the ratio of “near intercepts” of the demand curves for employees in hierarchies
, which appears throughout the paper, represents the ratio of “near intercepts” of the demand curves for employees in hierarchies 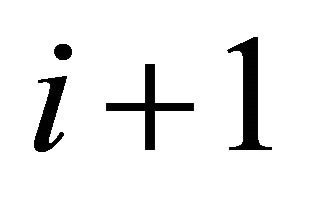 and i. When
and i. When 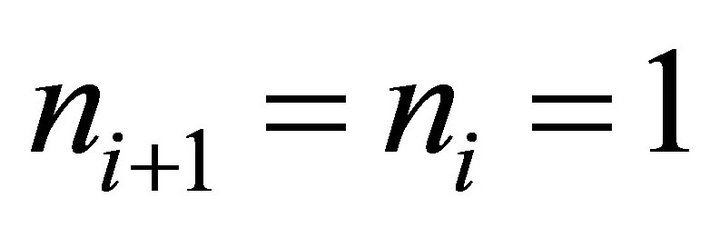 we expect the demand curve for employees of a greater hierarchy,
we expect the demand curve for employees of a greater hierarchy, 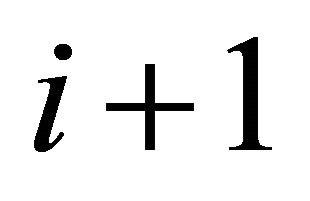 , to have a greater intercept than that of the lower hierarchy, i. It follows that we expect
, to have a greater intercept than that of the lower hierarchy, i. It follows that we expect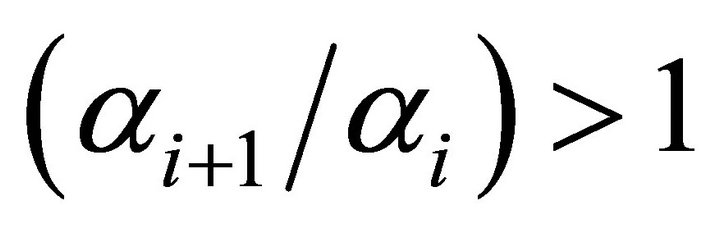 .
.
Equation (2) does not explicitly contain the measure of ability, Hi, but it is indirectly related since the number of individuals in any employee hierarchy of level i will be determined by some probability distribution relating the level of ability, Hi, to the relative number of individuals, ni that possess that ability level and are thereby included in that category. Therefore we can substitute 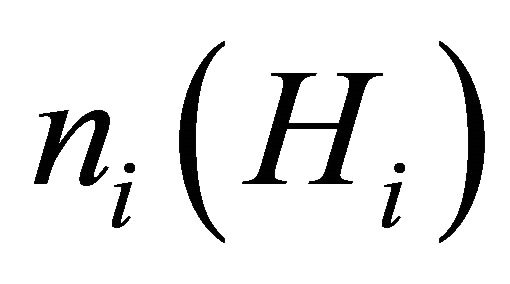 for ni in Equation (2) producing:
for ni in Equation (2) producing:
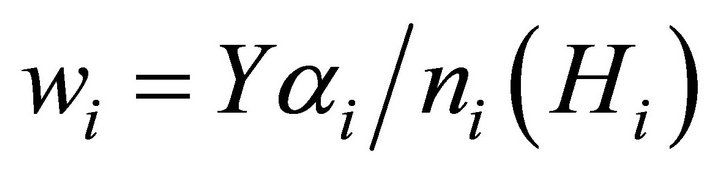 (3)
(3)
4. The Distribution of Ability and Elasticity
A progressive wage or salary system exists when the elasticity of the wage or salary with respect to the measure of potential ability is greater than unity. The elasticity is above unity if the percentage change in the wage or salary, divided by the percentage change in the measure of ability, is above unity, or:
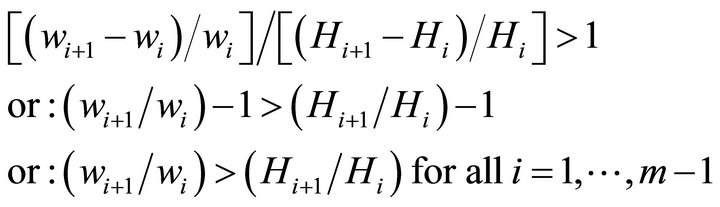 (4)
(4)
Using Equation (3) for the wage on the left of Equation (4) the condition for the elasticity of wages with respect to the measure of ability to be above unity is:
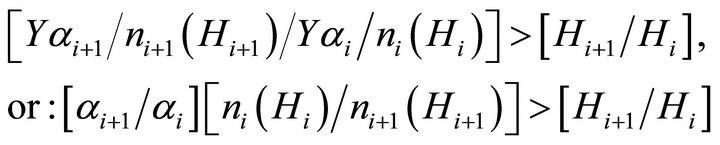 (5)
(5)
Condition (5) crucially depends on the current number of individuals, ni and ni+1 in adjacent hierarchies of employment. As noted above, Hi and ni are linked by some distribution relating the measure of ability Hi to the number of such individuals ni that have the required level of ability to be hired in hierarchy i. A reasonable assumption is that ability among potential employees has a continuous bell-shaped distribution. In other words, there are relatively few with below average and above average ability but a large number with average ability. This is the assumption made by Neal and Rosen [12]. Such continuous distributions, however, seldom yield closed-form solutions and become difficult to analyze. Alternatively, since the Poisson distribution can be used to approximate a normal distribution, we approximate ability across the m hierarchies of employees using a discrete Poisson distribution. Others have suggested that when using data for only the very best employees, i.e., when only the upper tail of the normal distribution of ability is used, then the Yule-Simon distribution could be used, as it resembles the upper tail of the normal distribution. Appendix B contains the alternative results of this paper if that assumption is appropriate. For most situations, however, the Poisson probability function is preferred since it allows for bell-shaped distributions and can be used to approximate the normal distribution. Its probability density function is given by:
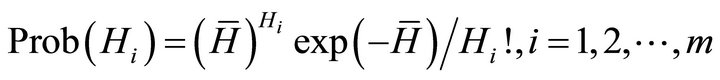 (6)
(6)
In the Poisson distribution there are m distinct hierarchies of employment and  is the mean of the distribution. As the number of hierarchies becomes large, the discrete Poisson distribution approximates the normal distribution. If N is the total number of employees in all hierarchies of employment in a particular field, the predicted number of employees in each hierarchy i is:
is the mean of the distribution. As the number of hierarchies becomes large, the discrete Poisson distribution approximates the normal distribution. If N is the total number of employees in all hierarchies of employment in a particular field, the predicted number of employees in each hierarchy i is: , where N is the total number of potential employees for all hierarchies. This allows us to substitute for ni and ni+1 on the left side of Equation (5). Thus for every i and i+1 in Equation (5) we have:
, where N is the total number of potential employees for all hierarchies. This allows us to substitute for ni and ni+1 on the left side of Equation (5). Thus for every i and i+1 in Equation (5) we have:
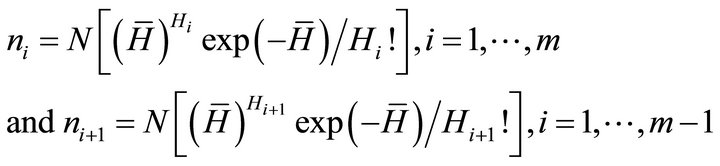 (7)
(7)
The measure of ability, Hi, can be treated as having cardinal properties since we are interested in the elasticity and thus its percentage change. Here, for simplicity, we assume that the measure of ability takes on successive integer values such that 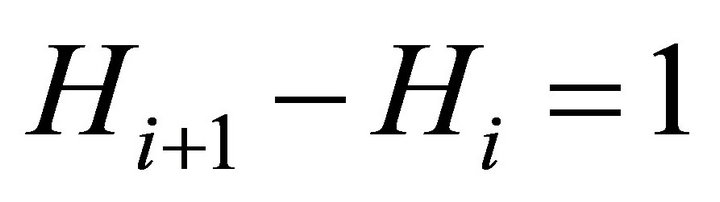 for all i. This would be true for many measures of human capital stock, e.g., discrete test scores, or years of education, or some measure of the quality of the education or training of an institution. Under this assumption, where Hi+1 and Hi take on successive integer values, both
for all i. This would be true for many measures of human capital stock, e.g., discrete test scores, or years of education, or some measure of the quality of the education or training of an institution. Under this assumption, where Hi+1 and Hi take on successive integer values, both 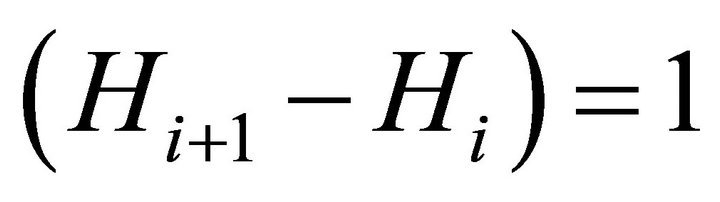 and
and 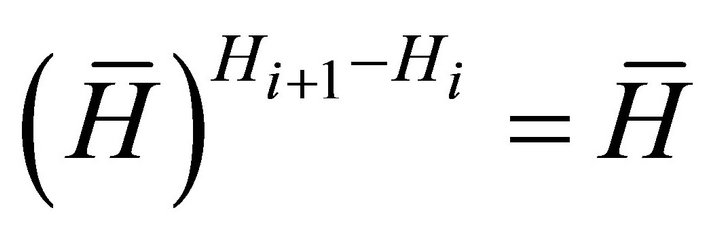 . In addition it is always true that
. In addition it is always true that 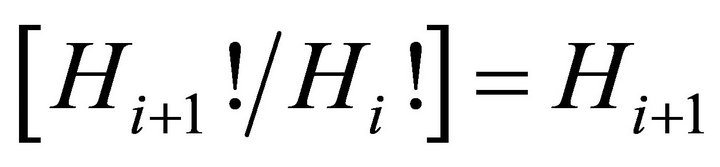 . Using these facts and substituting the results of Equation (7) into Equation (5), the elasticity of salary with respect to changes in the measure of ability,
. Using these facts and substituting the results of Equation (7) into Equation (5), the elasticity of salary with respect to changes in the measure of ability, ![]() , is:
, is:
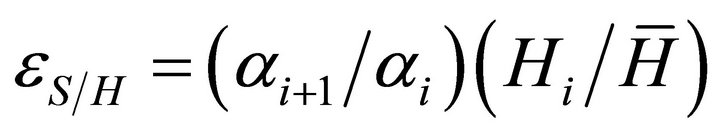 (8)
(8)
We see from Equation (8) that the ratio of production elasticities, 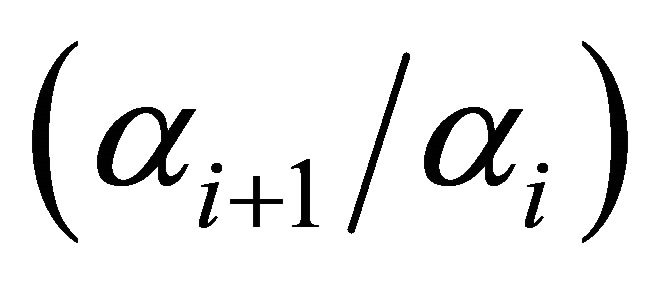 , is crucial to the resulting condition. The ratio, as noted above, is expected to be greater than one, but not highly greater than one if there are many hierarchies. Nevertheless, even if the ratio is close to unity a greater elasticity of salary or wage relative to ability will depend primarily on the ratio
, is crucial to the resulting condition. The ratio, as noted above, is expected to be greater than one, but not highly greater than one if there are many hierarchies. Nevertheless, even if the ratio is close to unity a greater elasticity of salary or wage relative to ability will depend primarily on the ratio 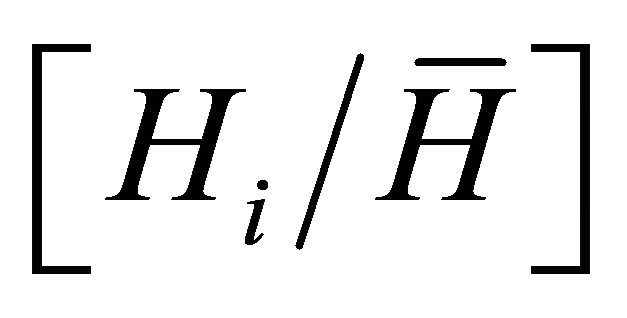 . In this case the elasticity of compensation relative to the measure of ability,
. In this case the elasticity of compensation relative to the measure of ability, ![]() , will always increase with increases in the hierarchy under consideration.
, will always increase with increases in the hierarchy under consideration.
Equation (8) can be rearranged in order to obtain the condition under which the elasticity, εS/H, will be greater than unity, yielding the progressive salary result.
Condition: For a system with discrete measures of ability as described above, the condition that the elasticity of salary with respect to ability above unity is (Appendix A):
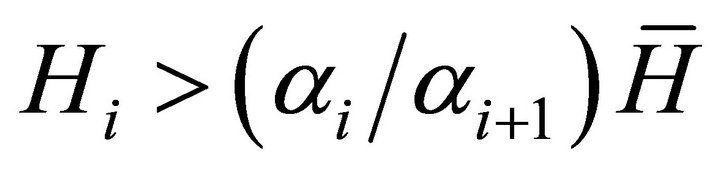 (9)
(9)
The condition (Equation (9)) that the elasticity of compensation with respect to the measure of ability be greater than unity depends on the relative demand components, 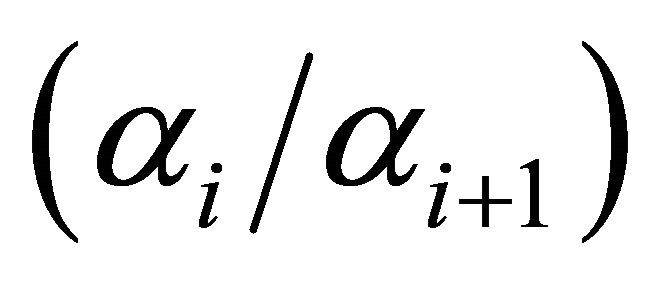 , and the mean of the distribution of ability,
, and the mean of the distribution of ability,  . If there are many hierarchies,
. If there are many hierarchies, 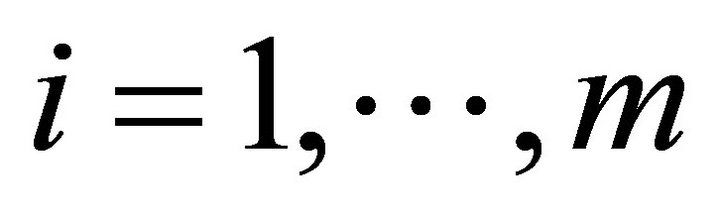 , then it is expected that
, then it is expected that 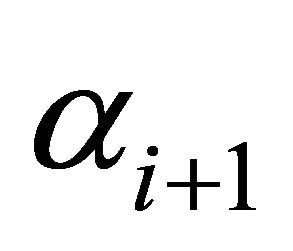 and
and 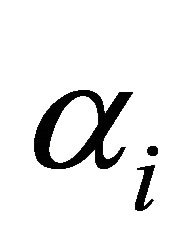 are fairly close in value. In this situation the progressive salary schedule holds for any level of ability above the mean ability level
are fairly close in value. In this situation the progressive salary schedule holds for any level of ability above the mean ability level  . When
. When 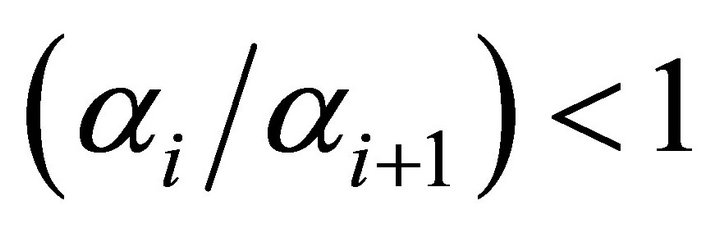 (the expected case) the progressive salary structure exists at values of ability less than the mean
(the expected case) the progressive salary structure exists at values of ability less than the mean  , and if under some condition we have
, and if under some condition we have 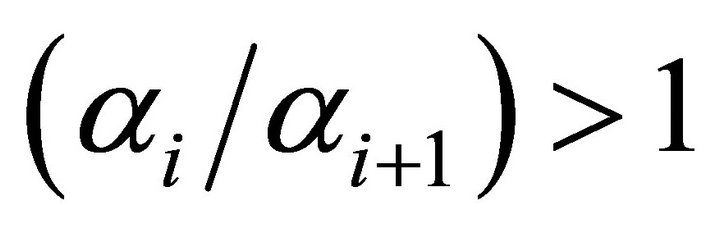 it occurs at values greater than the mean.
it occurs at values greater than the mean.
Both supply and demand conditions are required in this result. The elasticity of salary with respect to ability is above unity in the upper tail of the distribution of ability. Like the MSV model it qualifies as an example of the superstar phenomenon, but unlike the MSV model it does not require a separate hierarchy of employee that receives a share of profits rather than a higher salary based on the value of the marginal product within the hierarchy. The usual bell-shaped distribution of ability and a greater demand for more potentially able employees results in a progressive salary structure in the upper tail of the distribution of ability. This is also a condition which supports the superstar phenomenon with the minimum of assumptions concerning the distribution of ability and the demand for more able employees.
5. An Application
An example of the elasticity of compensation with respect to ability can be observed by examining Stanford University’s MBA program. In 2006 the average Graduate Management Admission Test (GMAT) score of entering students in all MBA programs was 560 [13] while the GMAT score for students entering Stanford’s MBA program was 720 [14]. Thus Stanford’s average GMAT score is approximately 29% higher than the national average. The average outgoing salary for all MBAs was $53,490 [15] while the average for Stanford was $165,500 [16]. The Stanford salary for graduating MBAs was approximately 209% above the national average. One measure of the elasticity of the differences between Stanford’s program and the national average is 7.22 (= 209%/29%).
For a more inclusive analysis we make use of a sample of 894 observations collected over seven years and 226 different MBA programs in the USA. The data is obtained from the various published editions of Miller [17]. As a measure of ability we use the average GMAT scores of entering students. A smaller sample of the data was initially used by Hamlen and Southwick [18] to examine the relationship between input ability and output salaries for MBA programs. Figure 1 shows average outgoing salaries (all in real terms) plotted against average GMAT scores. From Figure 1 it is not difficult to predict that the elasticity of compensation with respect to ability will be higher for the upper level hierarchies of ability.
One convenient functional relationship that associates average outgoing salary with average GMAT score is obtained by using a cubic regression of average salary as a function of GMAT score. The cubic regression adequately captures changes in slope and can be justified by the Stone-Weierstrass [19] theorem that states that any continuous function can be approximated to any degree of accuracy by a polynomial of finite degree. Using a polynomial of degree greater than three results in strong multicollinearity (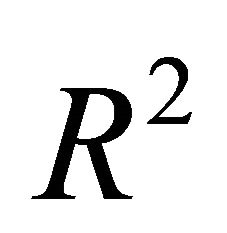 approaching 1). The result of the cubic regression, with
approaching 1). The result of the cubic regression, with 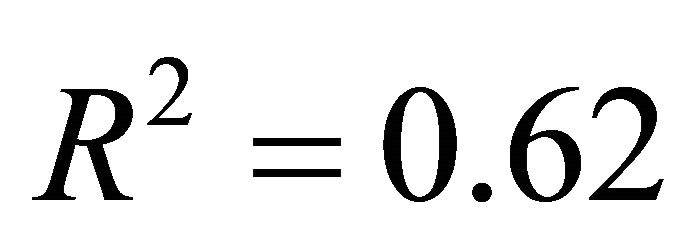 and t-values given in parenthesis, is:
and t-values given in parenthesis, is:
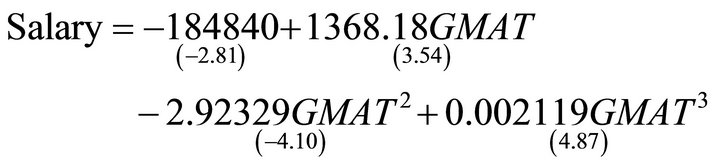 (10)
(10)
In Figure 1 the curved line within the data is based on predicted salaries using Equation (9). In Figure 2, using Equation (10), the estimated point elasticity of salary with respect to GMAT score is calculated and plotted against the average GMAT score.
In agreement with the condition given by Equation (9), the elasticity is greater than unity for GMAT scores above the mean, GMAT = 560. The fact that the elasticity begins to exceed unity for values of GMAT scores slightly below the mean suggests, within the context of the above model, that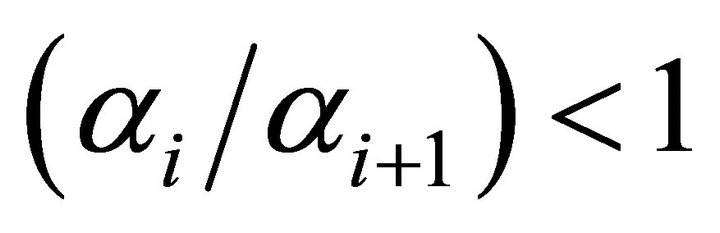 . We find that the results agree with the predictions of the model. The elasticity of average out-
. We find that the results agree with the predictions of the model. The elasticity of average out-
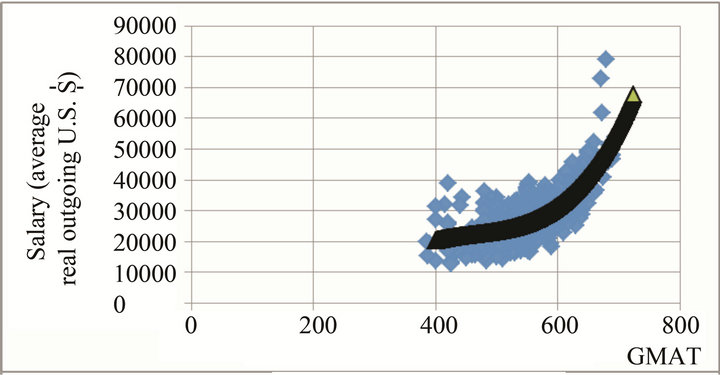
Figure 1. Salary plotted against GMAT scores.
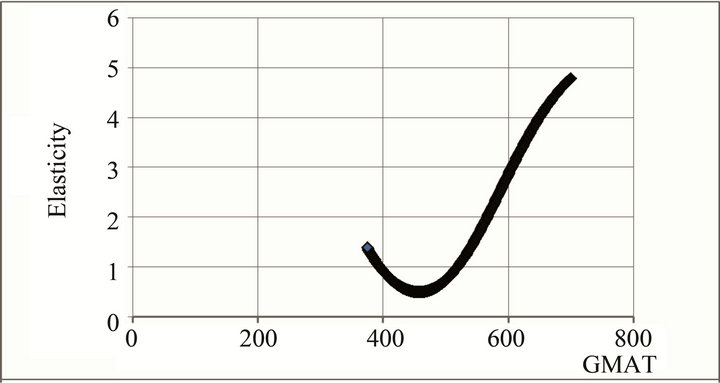
Figure 2. Estimated point elasticity.
going salary with respect to average GMAT score is approximately 0.49 for programs with below-average GMAT scores and approximately 1.77 for all programs with above-average GMAT scores.
As predicted, the progressive salary structure with respect to potential ability becomes highly elastic (statistically) when only the MBA programs with above-average GMAT scores are included, while those programs with below-average GMAT scores exhibit a low, inelastic relationship between compensation and potential ability. In essence, a greater demand for more able employees is matched with a smaller supply of such employees to produce a definite progressive salary in the upper tail of the distribution of potential ability.
6. Summary
Using standard assumptions regarding production and ability, and following Rosen’s [1] hierarchy structure, we find that progressivity of salary with respect to ability exists for employees with above average ability. Since it exists in the upper tail of the distribution of ability, this implies, as described by Rosen [2], that there is a superstar phenomenon. Within the same context, if only the upper tail of the normal distribution of ability is examined and the Yule-Simon distribution [9] is appropriate, the progressive salary condition occurs for all hierarchies of employees.
The model was tested using average beginning salaries from various MBA programs in the USA and average test scores from the same programs. The elasticity of salary with respect to test scores was below unity for programs with below average test scores and above unity for programs with above average test scores. In addition the elasticity increases as the average test score increases.
REFERENCES
- S. Rosen, “Authority, Control, and the Distribution of Earnings,” The Bell Journal of Economics, Vol. 13, No. 2, 1982, pp. 311-323. doi:10.2307/3003456
- S. Rosen, “The Economics of Superstars,” The American Economic Review, Vol. 71, No. 5, 1981, pp. 845-858.
- A. Marshall, “Principles of Economics,” 8th Edition, MacMillan, New York, 1947.
- G. W. Scully, “Pay and Performance in Major League Baseball,” The American Economic Review, Vol. 64, No. 6, 1974, pp. 915-930.
- J. C. H. Jones and W. D. Walsh, “Salary Determination in the National Hockey League: The Effects of Skills, Franchise Characteristics, and Discrimination,” Industrial and Labor Relations Review, Vol. 41, No. 4, 1988, pp. 592-604. doi:10.2307/2523593
- W. Hamlen, “Superstardom in Popular Music: Empirical Evidence,” The Review of Economics and Statistics, Vol. 73, No. 4, 1991, pp. 729-733. doi:10.2307/2109415
- W. A. Hamlen Jr. “Variety and Superstardom in Popular Music,” Economic Inquiry, Vol. 32, No. 3, 1994, pp. 395- 406. doi:10.1111/j.1465-7295.1994.tb01338.x
- K. H. Chung and A. K. Cox, “A Stochastic Model of Superstardom: An Application of the Yule Distribution,” The Review of Economics and Statistics, Vol. 76, No. 4, 1994, pp. 771-775. doi:10.2307/2109778
- C. Lucifora and R. Simmons, “Superstar Effects in Sport: Evidence from Italian Soccer,” Journal of Sports Economics, Vol. 4, No. 1, 2003, pp. 35-55. doi:10.1177/1527002502239657
- K. M. Murphy, A. Shleifer and R. W. Vishny, “The Allocation of Talent: Implications for Growth,” The Quarterly Journal of Economics, Vol. 106, No. 2, 1991, pp. 503-530. doi:10.2307/2937945
- J. G. Witte, “The Microfoundations of the Social Investment Function,” Journal of Political Economy, Vol. 71, No. 5, 1963, pp. 441- 456. doi:10.1086/258793
- D. Neal and S. Rosen, “Theories of the Distribution of Earnings,” In: A. B. Atkinson and F. Bourguignon, Eds., Handbook of Income Distribution, North-Holland, New York, 2000, pp. 379-427. doi:10.1016/S1574-0056(00)80010-X
- K. Schweitzer, “Taking the GMAT—GMAT Score,” 2006. http://businessmajors.about.com/od/satgmatpreparation/a/GMATscores.htm
- “Average MBA Starting Salaries at the Top Business Schools,” 2006. http://www.admissionsconsultants.com/mba/compensation.asp
- “Salary Survey Report,” 2006. http://www.payscale.com/research/US/Degree=Master of Business Administration (MBA)/Salary
- “Admissions to Business Schools,” 2006. http://education.yahoo.com/college/essential/articles/biz/bschool-admissions.html
- E. Miller, “Barron’s Guide to Graduate Business Schools,” Barron’s Educational Series, Inc., Hauppauge, 1988, 1990, 1992, 1994, 1997, 1999, 2005.
- W. Hamlen and S. Southwick, “Output in MBA Programs: Inputs, Outputs or Value Added?” Journal of Economic and Social Measurement, Vol. 15, No. 1, 1989, pp. 1-26.
- M. Stone, “The Generalized Weierstrass Approximation Theorem,” Mathematics Magazine, Vol. 21, No. 4, 1948, pp. 167-184.
Appendix A
In this appendix the general condition that the elasticity of compensation with respect to ability is greater than unity is given by Equation (9).
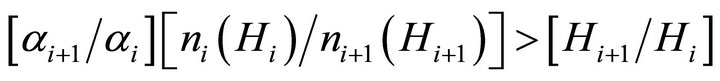 (A1)
(A1)
If the Poisson distribution of ability is assumed and given by Equations (6) and (7), Equation (A1) becomes:
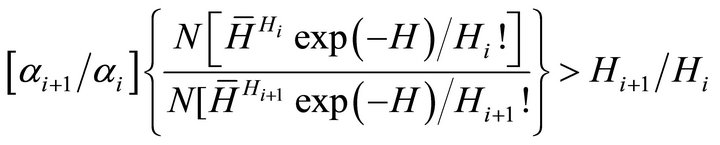 (A2)
(A2)
Equation (A2) reduces to:
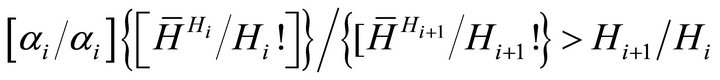 (A3)
(A3)
This, in turn, reduces to:
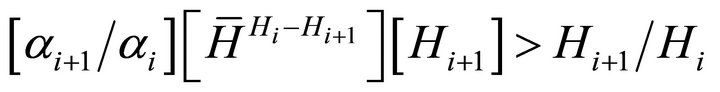 (A4)
(A4)
Given that 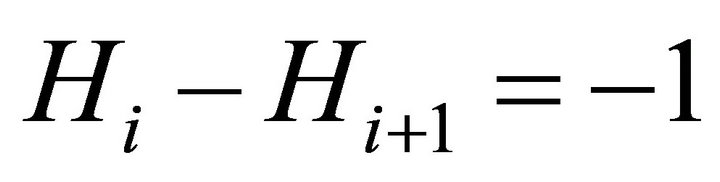 and
and 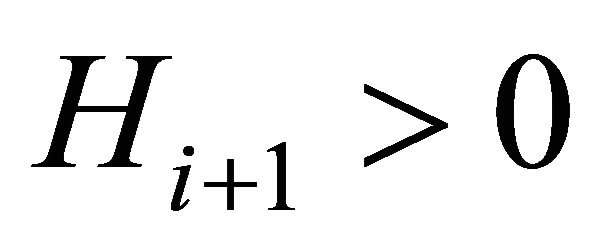 can be eliminated from both sides of Equation (A4), we obtain:
can be eliminated from both sides of Equation (A4), we obtain:
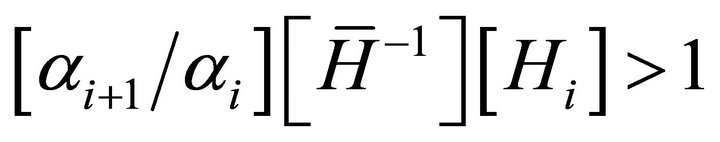 (A5)
(A5)
Finally rearranging Equation (A5) we have the condition given by Equation (9).
Appendix B
In this appendix we find that the Yule-Simon distribution yields an elasticity of compensation relative to ability to be greater than unity as long as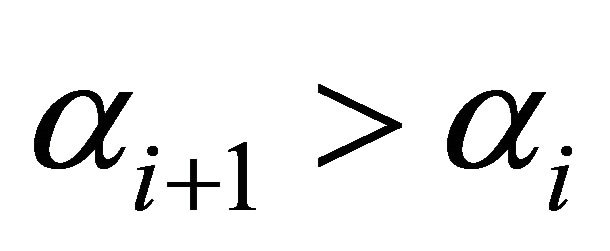 . The probability density function for the Yule-Simon distribution is:
. The probability density function for the Yule-Simon distribution is:
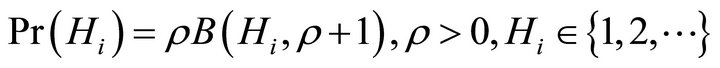 (B1)
(B1)
with 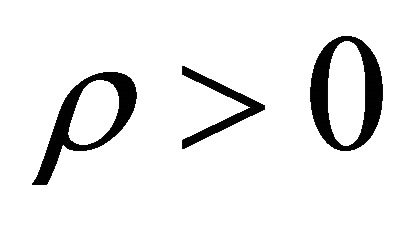 and
and 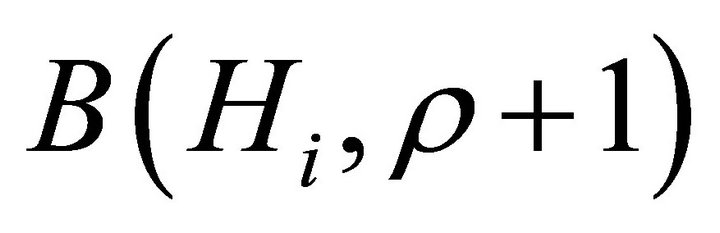 is the beta distribution. This is given here by:
is the beta distribution. This is given here by:
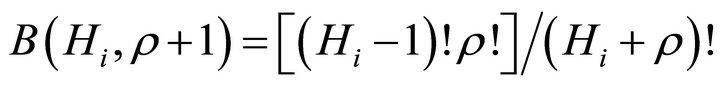 (B2)
(B2)
Substituting (B1) and (B2) into Equations (6) and (7) the condition that the elasticity of salary with respect to ability be greater than one becomes:
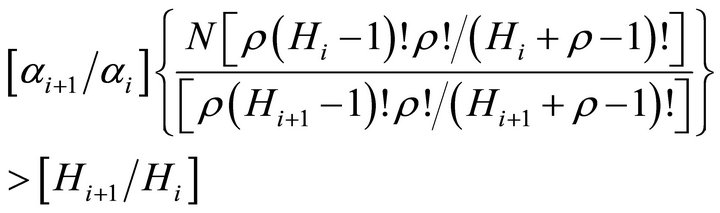 (B3)
(B3)
Equation (B3) reduces to:
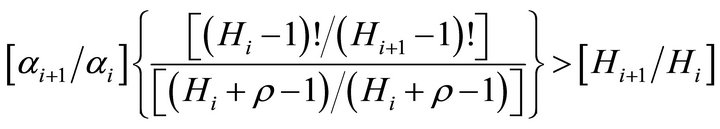 (B4)
(B4)
It further reduces to:
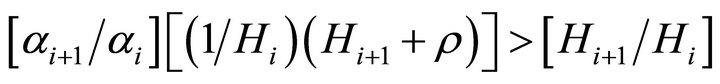 (B5)
(B5)
This yields the final result that assuming a Yule-Simon distribution of ability the condition that the elasticity of salary with respect to the measure of ability be greater than unity requires that:
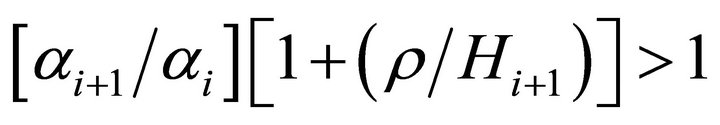 (B6)
(B6)
Since we have assumed that 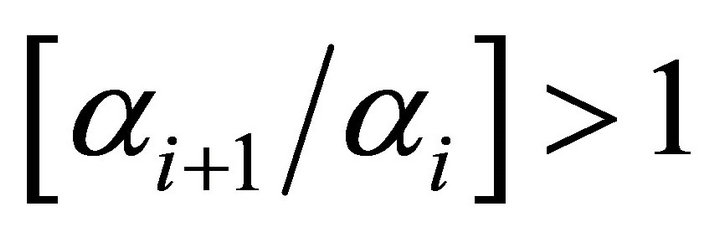 and ρ and
and ρ and ![]() are both positive, then the elasticity of salary with respect to ability is greater than unity for all
are both positive, then the elasticity of salary with respect to ability is greater than unity for all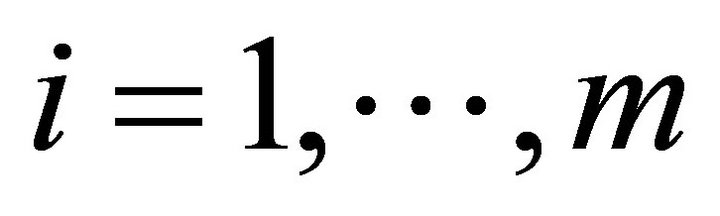 . Thus if we assume that only the upper tail of the normal distribution is contained within the data set, and this can be approximated by a Yule-Simon distribution, then a progressive or superstar compensation system will exist at all levels of ability.
. Thus if we assume that only the upper tail of the normal distribution is contained within the data set, and this can be approximated by a Yule-Simon distribution, then a progressive or superstar compensation system will exist at all levels of ability.

