Theoretical Economics Letters
Vol. 2 No. 5 (2012) , Article ID: 25535 , 4 pages DOI:10.4236/tel.2012.25077
A Model of the Religious Transition
1University of Hamburg, Hamburg, Germany
2German Institute of Global and Area Studies, Hamburg, Germany
3Department of Economics and Business, Aarhus University, Aarhus, Denmark
Email: gundlach@giga-hamburg.de, mpaldam@econ.au.dk
Received May 20, 2012; revised June 22, 2012; accepted July 25, 2012
Keywords: Religious Transition; Religiosity; Religious Beliefs; Solow Model
ABSTRACT
The religious transition is the decline of religiosity with rising levels of income. The empirical robustness of the transition has been demonstrated. It appears that the transition is driven by the substitution of scientific knowledge for religious beliefs, which characterizes the process of modern economic growth. This note models the substitution process. A Solow model with CES technology generates the transition path with endogenous growth and reveals a direct link between the substitution parameter and the estimated transition parameter.
1. Introduction
The religious transition is the decline in religiosity that follows from rising levels of income. The process has been analyzed empirically in Paldam and Gundlach [1] and [2]. This note is an attempt to explain the empirical results in the context of a simple growth model.
A religion is a particular bundle of largely immaterial ideas and beliefs. It is almost constant, though the bundle is adjusted marginally in the long run. Religiosity is the intensity by which people use their religion. That is, religiosity is the importance of (any) religion in all aspects of life. Religiosity is much more variable than religious beliefs.
In Paldam and Gundlach [1], religiosity is measured as an R-variable that is the dominating factor in 14 polled items from the World Values Survey [3]. These items are chosen to span as many religious aspects as possible. The R-variable is reported to be robust to changes in the composition of countries and items in the sample. With this operationalization of religiosity, a strong transition path becomes visible both over time and across countries. The transition path from high to low religiosity can be described by the function , where income
, where income 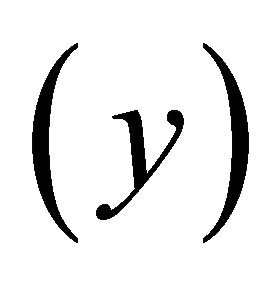 is measured as (log) GDP per capita. The function is governed by the transition parameter, which is reported to be robust across alternative samples and specifications.
is measured as (log) GDP per capita. The function is governed by the transition parameter, which is reported to be robust across alternative samples and specifications.
In low income countries, religiosity is roughly twice as high as in high income countries. While the empirical facts are strong and robust, the explanation of the facts is more debatable, especially as the demand for religion is both for consumption and as a factor of production. Some explanations have been sketched in Paldam and Gundlach [1]. A key factor in the explanations is substitution. In the process of development, religious beliefs are replaced by scientific knowledge as a factor of production and religious institutions are replaced by secular institutions as a provider of collective goods such as education, healthcare, and social security.
We develop a simple Solow growth model with CESproduction technology to explain the religious transition as a substitution process. The model uses two factors of production: Religious beliefs and scientific knowledge. Endogenous economic growth is driven by a sufficiently high elasticity of substitution, where religious beliefs (and religious institutions) are replaced by scientific knowledge (and secular institutions). In this setting, the implicit factor share of religious beliefs falls with rising levels of income, even in the presence of a constant stock of religious beliefs. We interpret the observed decline of the empirical measure of religiosity R as the declining factor share of religious beliefs and show that the empirical estimate of the implied transition parameter is related to the substitution parameter of the CES technology.
2. A Religious Solow Model with Endogenous Growth
We consider an economy that produces a single output good with two factor inputs. The factor inputs are nonstandard: religious beliefs B and scientific knowledge , rather than labor and capital. The two factor inputs represent alternative ways of decision making that lead to different levels of output. It is assumed that the stock of religious beliefs is constant, while the stock of scientific knowledge can be accumulated over time t. The stock of religious beliefs is maintained by religious institutions and the stock of scientific knowledge is maintained by secular institutions, such that any substitution of a factor of production is assumed to represent a proportional substitution of the respective institution (and vice versa)1. Each factor input has diminishing returns and is substitutable. Population is constant and normalized to 1. There is no exogenous technological change.
, rather than labor and capital. The two factor inputs represent alternative ways of decision making that lead to different levels of output. It is assumed that the stock of religious beliefs is constant, while the stock of scientific knowledge can be accumulated over time t. The stock of religious beliefs is maintained by religious institutions and the stock of scientific knowledge is maintained by secular institutions, such that any substitution of a factor of production is assumed to represent a proportional substitution of the respective institution (and vice versa)1. Each factor input has diminishing returns and is substitutable. Population is constant and normalized to 1. There is no exogenous technological change.
Given these assumptions, the output of the economy at time t is produced according to a CES production function
 , (1)
, (1)
where 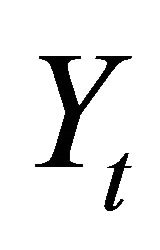 is real output,
is real output,  is the stock of accumulated scientific knowledge, B is the constant stock of religious beliefs, and A, δ, and ρ are parameters of scale, distribution, and substitution, which are assumed to satisfy the standard assumptions
is the stock of accumulated scientific knowledge, B is the constant stock of religious beliefs, and A, δ, and ρ are parameters of scale, distribution, and substitution, which are assumed to satisfy the standard assumptions  2.
2.
The elasticity of substitution,  , is given by
, is given by
 . (2)
. (2)
Dividing both sides of Equation (1) by B generates the intensive form as
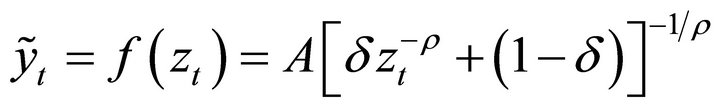 , (3)
, (3)
with  and
and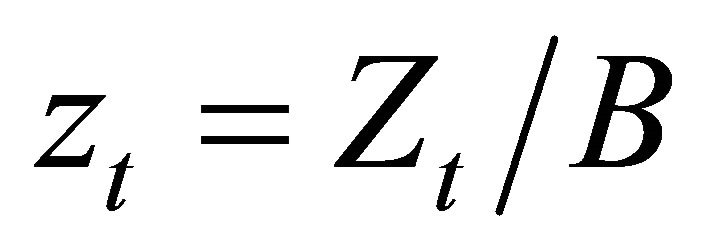 . A constant fraction of output
. A constant fraction of output 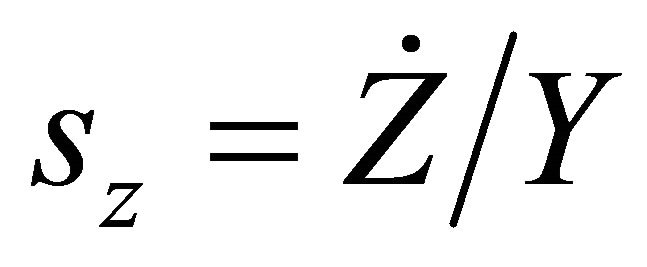 is saved and invested to generate new scientific knowledge. The stock of scientific knowledge depreciates with a constant rate
is saved and invested to generate new scientific knowledge. The stock of scientific knowledge depreciates with a constant rate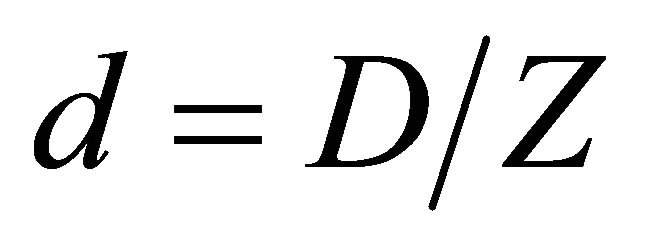 . The growth rate of the economy,
. The growth rate of the economy, 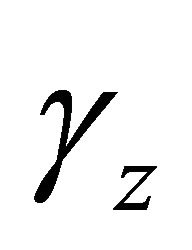 , is given by the difference between the rates of knowledge accumulation and depreciation as
, is given by the difference between the rates of knowledge accumulation and depreciation as
 . (4)
. (4)
As z goes to infinity, the first term of Equation (4) approaches a positive constant if the elasticity of substitution is larger than 1. As is well known3, the CES technology with 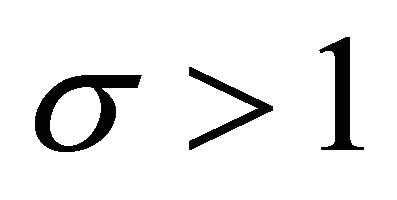 generates endogenous income growth if the parameters satisfy the inequality condition
generates endogenous income growth if the parameters satisfy the inequality condition
 (5)
(5)
This is shown in Figure 1. Whenever the marginal product of scientific knowledge (more generally, the marginal product of the input that can be accumulated) asymptotically achieves some lower bound that is greater than zero and larger than the value of the rate of depreciation, there will be a positive long-run rate of growth. Exogenous technological progress is not needed in this model as the engine of growth as long as the elasticity of substitution between scientific knowledge and religious beliefs is high enough to guarantee that the two curves in Figure 1 do not cross.
This simple growth model captures an important aspect of the observed long-run religious transition. The CES production function allows for output in the presence of only one of the inputs4. With no scientific knowledge, there is no substitution and hence no longrun growth, but there will be output in the presence of religious beliefs, . So the modeling framework is in line with the Malthusian stagnation and the dominance of religious beliefs before the Industrial Revolution and with the rise of scientific knowledge and modern economic growth thereafter.
. So the modeling framework is in line with the Malthusian stagnation and the dominance of religious beliefs before the Industrial Revolution and with the rise of scientific knowledge and modern economic growth thereafter.
3. The Path of Religiosity in the Religious Solow Model
Religiosity R is defined as the weight of religious beliefs in decision-making. In the religious Solow model, R is interpreted as the weight of B in the production process. This weight is represented by the factor share  of B, hence
of B, hence .
.
In a CES specification, the factor shares are functions of the distribution parameter, the substitution parameter, and the values of the factor inputs. The factor shares of B and Z are given by:
 (6)
(6)

Figure 1. Endogenous growth with scientific knowledge accumulation and constant religious beliefs.
With scientific knowledge rising to infinity and constant religious beliefs, the factor share of scientific knowledge will approach 100% in the limit 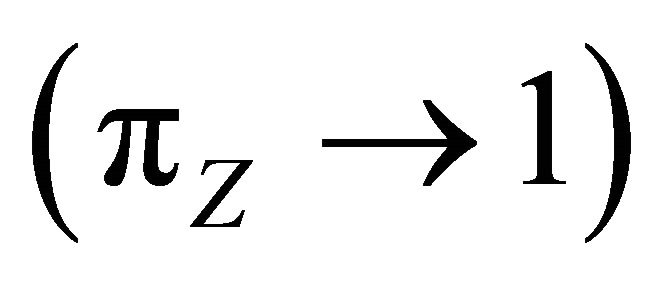 if
if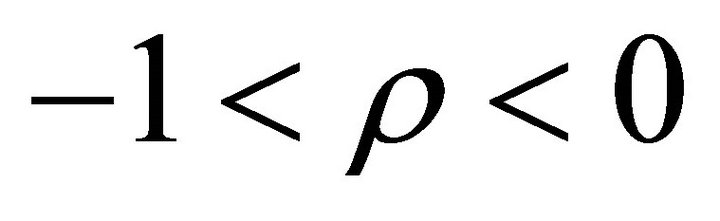 , i.e., if
, i.e., if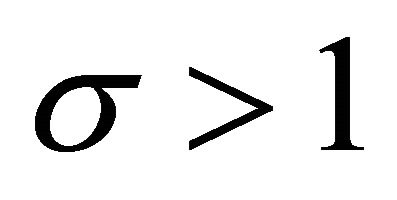 . By implication, the factor share of religious beliefs will approach zero in the limit
. By implication, the factor share of religious beliefs will approach zero in the limit 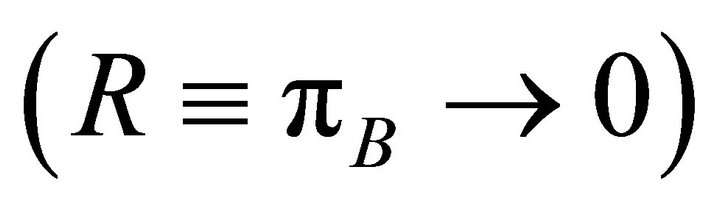 with rising scientific knowledge.
with rising scientific knowledge.
Rising scientific knowledge implies rising income because the substitution of Z for B is the engine of growth in this model. The decline of  that is generated by this endogenous growth is interpreted as the path of religiosity in the religious Solow model.
that is generated by this endogenous growth is interpreted as the path of religiosity in the religious Solow model.
The transition path starts at a high level of religiosity, 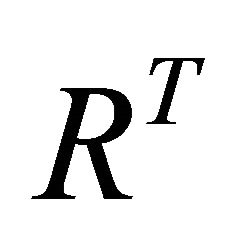 , which is typical for a traditional society where Z is approximately equal to zero. For Z → ∞, the level of religiosity approaches the modern level
, which is typical for a traditional society where Z is approximately equal to zero. For Z → ∞, the level of religiosity approaches the modern level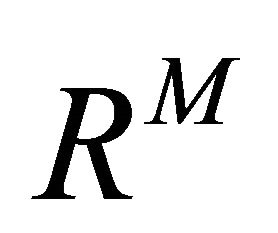 , which is predicted to be zero by the present model but which might turn out to be a non-zero constant if some decisions in life will remain to be determined by religious beliefs, independent of the level of scientific knowledge accumulation5. Thus, the model predicts that the transition path looks like the path in Figure 1(b) in Paldam and Gundlach [1].
, which is predicted to be zero by the present model but which might turn out to be a non-zero constant if some decisions in life will remain to be determined by religious beliefs, independent of the level of scientific knowledge accumulation5. Thus, the model predicts that the transition path looks like the path in Figure 1(b) in Paldam and Gundlach [1].
4. Assessing the Empirical Relevance of the Model of the Religious Transition
Endogenous growth generated by a CES technology with  has been considered empirically implausible because it implies long-run trends of factor shares. Traditional factor shares of capital and labor appear to be trendless around one third and two thirds of total factor income. However, our empirical measure of religiosity does have a long-run trend, which is in line with our interpretation of religiosity as a factor share in the context of a CES technology.
has been considered empirically implausible because it implies long-run trends of factor shares. Traditional factor shares of capital and labor appear to be trendless around one third and two thirds of total factor income. However, our empirical measure of religiosity does have a long-run trend, which is in line with our interpretation of religiosity as a factor share in the context of a CES technology.
Our interpretation invites the question whether and how the parameters of the religious Solow model (1) can be related to the slope parameter of the regression models estimated in Paldam and Gundlach [1]. They are of the general form:
 , (7)
, (7)
where i is a country index,  is a regression constant,
is a regression constant,  is an error term, and
is an error term, and  is the transition parameter.
is the transition parameter.
Klump and de la Grandville [6] show that the steady state factor share of a normalized CES production function depends on the saving-investment rate and other parameters, including the substitution parameter. The saving-investment rate can be proxied by the level of per capita income. Using our own notation with population normalized to 1, the result by Klump and de la Grandville ([6], p. 290) reads
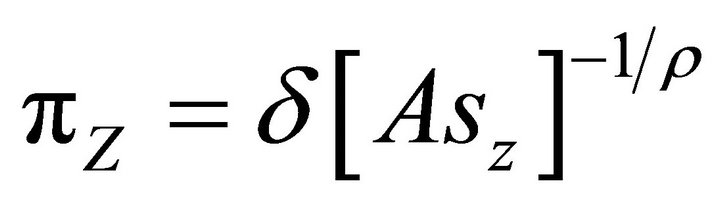 . (8)
. (8)
Assuming that 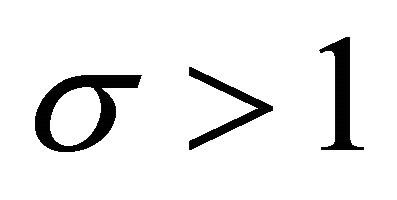 and hence
and hence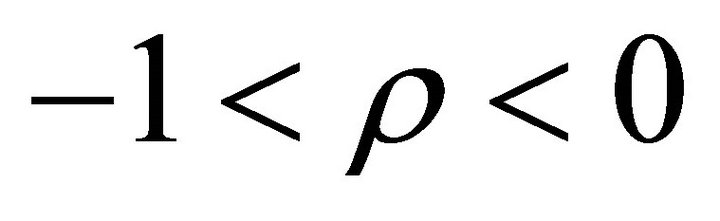 , Equation (9) predicts a positive relation between
, Equation (9) predicts a positive relation between 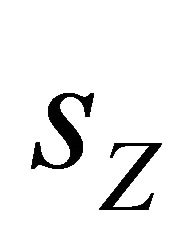 and
and . Since
. Since  and
and  add up to one, there must be a negative relation between
add up to one, there must be a negative relation between 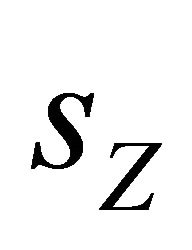 and
and  for
for 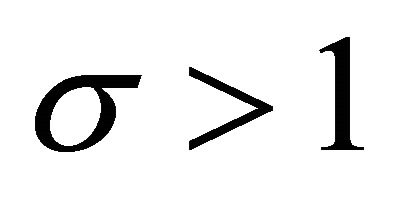 and hence a negative
and hence a negative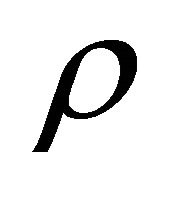 . Using the level of income
. Using the level of income 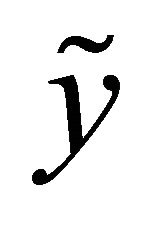 as a proxy for
as a proxy for 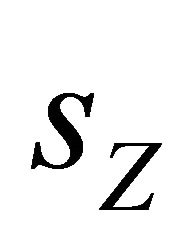 and taking logs, we find
and taking logs, we find
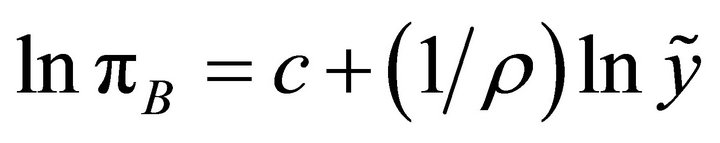 , (9)
, (9)
where  is a constant. Comparing Equation (9) with the regression Equation (7), it turns out that the estimated transition parameter,
is a constant. Comparing Equation (9) with the regression Equation (7), it turns out that the estimated transition parameter, 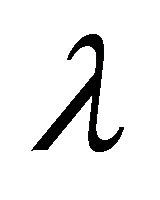 , can be interpreted as a proxy of the inverse of the substitution parameter, at least if the scaling of the variables is ignored:
, can be interpreted as a proxy of the inverse of the substitution parameter, at least if the scaling of the variables is ignored:
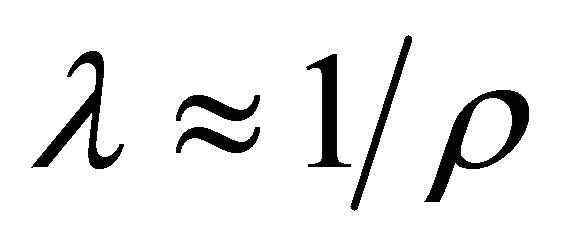 . (10)
. (10)
This conceptualization of the religious transition critically hinges on an elasticity of substitution that is larger than one. The more detailed discussion in Paldam and Gundlach (2012) of substitution processes on the supply side and the demand side motivate the hypothesis of a large elasticity of substitution between scientific knowledge and religious beliefs. Further research has to show whether this elasticity is in fact large enough to explain the observed decline in religiosity with the suggested model of the religious transition.
5. Concluding Remarks
We have made an effort to make the model of the religious transition as simple as possible and we trust that the reader will agree that the model follows from basic economic theory. It explains the religious transition as the outcome of an endogenous growth process that is driven by substitution, and it links the substitution parameter of the CES technology to the estimated transition parameter. As a model of long-run growth, it is also in line with the stagnation before the industrial revolution and the dynamics of growth thereafter.
6. Acknowledgements
We are grateful to all of those with whom we discussed the explanation of the empirical findings on the religious transition, notably to Leif Danziger.
REFERENCES
- M. Paldam and E. Gundlach, “The Religious Transition. A Long-Run Perspective,” Public Choice, 2012. doi:10.1007/s11127-012-9934-z
- M. Paldam and E. Gundlach, “Online Appendix to: The Religious Transition. A Long-Run Perspective,” 2012. http://www.martin.paldam.dk/Papers/GT-papers/Rel-Tra-Appendix.pdf
- World Values Survey. http://www.worldvaluessurvey.org
- R. M. Solow, “A Contribution to the Theory of Economic Growth,” Quarterly Journal of Economics, Vol. 70, No. 1, 1956, pp. 65-94. doi:10.2307/1884513
- K. J. Arrow, H. B. Chenery, B. S. Minhas and R. M. Solow, “Capital-Labor Substitution and Economic Efficiency,” The Review of Economics and Statistics, Vol. 43, No. 3, 1961, pp. 225-250. doi:10.2307/1927286
- R. Klump and O. de la Grandville, “Economic Growth and the Elasticity of Substitution: Two Theorems and Some Suggestions,” American Economic Review, Vol. 90, No. 1, 2000, pp. 282-291. doi:10.1257/aer.90.1.282
- R. J. Barro and X. Sala-i-Martin, “Economic Growth,” 2nd Edition, MIT Press, Cambridge, 2004.
NOTES
1There is competition between the two institutions; they may even fight.
2The CES production function was first suggested by Solow [4]. The functional form of the production function in Equation (1) was derived by Arrow et al. [5]. Our analysis also relies on the insight of Klump and de la Grandville [6].
3Several textbooks (e.g., Barro and Sala-i-Martin [7], pp. 68-71) present derivations of the standard equations used in the text, so they are not repeated.
4If Z = 0, the first term in (1) is not defined, but from Z → 0, we derive that (1) becomes AB, which is constant.
AB, which is constant.
5For instance, the weight of religious beliefs in matters of life and death, like decisions on suicide and abortion, may be stronger at any income level then decisions on marriage and divorce.

