Journal of Mathematical Finance
Vol.09 No.03(2019), Article ID:93121,10 pages
10.4236/jmf.2019.93012
Portfolio Selection in Mean-Minimum Return Level-Expected Bounded First Passage Time Framework
Tsotne Kutalia
Georgian American University, Tbilisi, Georgia
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 13, 2019; Accepted: June 17, 2019; Published: June 20, 2019
ABSTRACT
This paper explores the selection of optimal portfolio by replacing the standard Mean-Variance model by Mean-Minimum Return Level (MRL) framework and adding one important dimension—expectation of bounded First Passage Time (FPT) towards the MRL. To measure how much a given portfolio is exposed to risk, the new model can capture both, the amount of the largest possible loss at a certain confidence level and time to such an event occurring. The novelty of this paper is the introduction of bounded first passage time towards MRL and taking its expectation into consideration as an additional factor in portfolio selection decision making. Assuming that the asset price dynamics follow multi-dimensional Geometric Brownian Motion with drift, we obtain a portfolio wealth process for multiple assets and we evaluate the lowest possible value to which it can drop by a high confidence level. Then we extend our examination of the optimal portfolio selection by ultimately obtaining the efficient surface of risky portfolios. As a result, the paper shows that the third dimension can make a significant difference while choosing the asset weights compared to classical models ignoring the portfolio return paths as long as they achieve a desired combination of risk and return.
Keywords:
Multi-Dimensional Geometric Brownian Motion, Ito’s Process, Portfolio Optimization, Optimal Stopping Time

1. Introduction
Portfolio selection theories have gone through various improvements since the introduction of its most prominent theory by Harry Markowitz in 1952. He was first to introduce the risk-return principle with the well-known Mean-Variance framework. The basic idea is to arrive at an efficient frontier curve of risky assets by minimizing volatility for given expected returns. It is shown that taking more than one risky position can eliminate some portion of risk as an investor realizes the effect of diversification. Volatility as a risk measure is ideal when portfolio returns are normally distributed. However, when dealing with asymmetric distributions, it simply leads to misinterpretation of risk. Furthermore, in most of the cases, especially during abnormal economic states, history shows that markets do not follow the logic of normal distribution. In addition, measuring risk by volatility penalizes losses equally to profits of the same magnitude. However, investors are more concerned with a downside risk rather than simple volatility so that they are aware of the worst-case scenario that can be realized with a high degree of confidence. In addition, while aiming to select less correlated assets is a rational approach, there are some downsides we focus on. Slight change in correlation can cause significant change in MRL. At the same time, one may allocate funds into assets in proportions, which while being optimal in Mean-Variance sense, can cause hitting the MRL level faster by having overlooked one important factor—expected time of the portfolio return process towards the minimum level. This may be a source of severe problems for investors who are exposed to margin calls or need to raise funds in a short period of time if such an event is realized.
To account for the problem of measuring downside risk rather than simple dispersion, Value At Risk (VAR) was introduced by JP Morgan in the early 1990s. Since then, it has become a major benchmark instrument in the hands of financial institutions and regulators for measuring risk. Some theories appeared in the late 90s which promoted application of VAR and MaxVAR in portfolio management. Bookstaber and Richard [1] published a paper with some critical values about classical risk management. In 2004, Boudoukh et al. [2] did research about computing long horizon VAR for portfolios exposed to mark to marketing. In this paper it is shown that VAR is a very useful measure of risk in a mark to market environment and the way to compute it is explained. Basically, VAR is a statistical measure. Specifically, a quantile of losses at some confidence level indicates that the highest possible loss can be incurred in the worst-case scenario. There have been numerous methodologies for computing VAR in different circumstances. Expected Tail Loss (ETL, aka Expected Shortfall), defined as the average loss beyond VAR is a coherent risk measure according to Artzner et al. [3] (1999) and is widely used in risk calculation and portfolio optimization problems. Artzner et al. [3] provide a list of axioms a risk measure must satisfy in order to be coherent. Classical Markowitz optimization technique was translated into Mean-VAR (or Mean-ETL) framework and the usefulness of ETL was examined by Rockafellar et al. [4] (2000), where volatility is replaced by VAR (or ETL) and optimization is done based on minimization of VAR (or ETL) and maximization of expected returns of portfolio. While this approach is a step to the right direction when it comes to assessing worst possible risk that can be realized, it still lacks one important factor—expected time when the returns hit the lowest possible value at some confidence level. This is critically important for portfolios exposed to mark to marketing or margin calls. Adding this third dimension makes most of its sense when the portfolio volatility is large enough to cause the expected hitting time move before the investment horizon. In this scenario, one can differentiate portfolios by taking into account the expectation of hitting time bounded by the investment length. In case when portfolio variance is sufficiently low, the expectation of bounded hitting time coincides with the investment horizon and becomes an ignorable factor and an investor can stay within the two-dimensional Mean-MRL framework.
Lack of historical data or the complexity of parameter estimation forces investors to apply non parametric methods. Lin et al. [5] propose the portfolio optimization problem based on semi variance of uncertain variables. Within this model, the returns of assets are estimated based on experts’ subjective views. Models like uncertain semi variance have parameters which are hard to quantify, but in uncertain situations subjective views are useful or at least the only solution.
Closely related idea to the uncertain semi variance model is the semi absolute deviation model proposed by Qin et al. [6] . Within this paper, authors examine the portfolio selection by several mean-semi absolute deviation adjusting models to measure trade off between risk and return. Views about the asset returns are obtained from expert opinions like in semi-variance model.
Our aim is to construct a model which delivers the best performance in the sense that safety is taken as a priority. In order to concentrate on the contribution of the paper, we use Minimum Return Level as a risk measure instead of VAR or ETL. Once having MRLs and portfolio expected returns computed for different sets of asset weights, we extend the framework by introducing expected first passage time bounded by investment horizon as a third dimension used for decision making. This is done by computing the expectation of the minimum between the investment horizon and the first passage time of portfolio return process towards the minimum level. Once all three quantities for a given set of portfolio weights are in place, we define the best combination of them by maximizing MRL and the expected bounded first passage time for a given expected return of a portfolio. The ultimate result is the efficient surface of risky portfolios. This can be regarded as the three-dimensional counterpart to efficient frontier in classical Mean-Variance model.
As a comparison to the Mean-Variance model, while this model might suggest holding a certain weights in assets allocated within a given portfolio, the Mean-MRL-FPT model may reject it altogether and find a set of weights which is better in 3-dimensional sense. In addition, it is quite possible that the optimal portfolio weights found by the Mean-Variance framework produces a negative drift which is avoided by the Mean-MRL-FTP model. In a highly volatile environment, portfolio of assets selected by the Mean-Variance framework will hit the lowest possible return level earlier than the portfolio selected by Mean-MRL-FTP framework and at the same time, the latter includes the risk measured by variance as it is reflected in computation of MRL. So, there is a double benefit from applying MRL and FTP when the available assets are volatile enough.
The paper is structured in four main parts. The second section examines the differential equations which represent the multi-dimensional Ito’s processes and constructs the portfolio process. Within this section, it is shown that in order for the portfolio wealth to drop to its minimum level, the geometric Brownian motion that determines the portfolio wealth must reach the level which we call the Minimum Return Level. This brings us to the next, third section. In this section the MRL is formally defined according to its probability function. The fourth section overviews the third dimension of the model—expected bounded First Passage Time towards MRL. This value consists of two parts—the probability density function and the cumulative probability function of the First Passage Time. The final part, section five deals with the model construction. It combines all the three dimensions and obtains the efficient surface of risky portfolios.
2. Portfolio Wealth Process
Consider a portfolio consisting of n risky assets. [7] examines the multi-dimensional Brownian motions for self-financing portfolios.
To model the asset price movements, we take n-dimensional Ito’s process which is a vector of asset prices driven by n-dimensional Brownian motion , where be the real valued Brownian motion which starts from 0 on :
(2.1)
where is the drift and is the row vector . For more convenient notation we can convert the differential equation into the following form:
(2.2)
Define the portfolio wealth process corresponding to self-financing portfolio to follow the differential equation:
(2.3)
Since we only consider long portfolios, here
denotes the number of jth asset purchased at time
To solve this process, we extend the differential equation and introduce some notations. Let be the cash position of ith asset and let be the
weight of ith asset within a portfolio at time t. Having defined these quantities, we can proceed to solve the portfolio wealth process as follows:
(2.4)
Multiplying the terms, factoring out the like terms and converting the equation into terms yields:
(2.5)
At this point we have arrived to an equation defined in terms of dollar positions in each asset within a portfolio. However, since our ultimate goal is to optimize the asset weights, we need to convert this equation into the terms of . This is achieved by multiplying and diving the right side of the equation by at the same time. So, the result is an equation translated into weight terms:
(2.6)
Since the optimal weights imply an investor should hold these weights constant during an investment horizon, it means an investor should constantly rebalance the portfolio in order to maintain the once selected weights. So, assuming that weights are held constant at any point in time t, we can correspondingly update the Equation (2.6) into the form:
(2.7)
In this equation, all sums within the parenthesis are constants, so we can shorten the notation by introducing the new notations:
Let
and for all .
Equation (2.7) now becomes:
(2.8)
Solution to this differential equation by [7] is:
(2.9)
Power can be simplified once more if we let and represent the sum of Brownian motions as a single Brownian motion by adjusting the coefficients accordingly. So
where .
Finally, the portfolio wealth process is:
(2.10)
At this point, it is clear that the power:
(2.11)
So called return of the portfolio is a Brownian motion with drift and diffusion coefficients. Since it represents the rate at which the portfolio wealth is changing, .
3. Minimum Return Level
Given the portfolio wealth process by (2.10), it is clear that minimum portfolio wealth by high confidence level is reached when (2.11) obtains the lowest value by the same confidence level. In order to measure it, we need to know the probability distribution function of portfolio returns. Once we have estimated the probability distribution function F for portfolio returns, we can extract the quantile , where alpha is a significance level, usually taken to be 1% or 5%. The key improvement brought by the First Passage Time is that, if the estimated portfolio return probability density function does not turn out to be symmetric while the volatility is significantly large, then the portfolios’ expected bounded FPTs will often differ a lot. Graphically, if we denote MRL as , on a normal distribution density function, it looks as follows (Figure 1).
Figure 1. Normal probability density function corresponding to the cumulative probability function F. .
From now on we will use m as the lowest level for the returns process (2.11) to reach in order to obtain the lowest portfolio wealth.
4. Expectation of Bounded First Passage Time.
Next step is to define the new dimension—expectation of bounded first passage time.
For a Brownian motion with drift
(4.1)
if we denote the minimum value of this process till time t as:
(4.2)
and let be the first passage time to the level y, then it is shown from [8] that the probability distribution function for is given by:
(4.3)
where is the cumulative standard normal probability distribution function.
We are looking for the first passage time for the returns process given by (2.11) towards the level m (which we called MRL). m is usually a negative quantity (Figure 2).
We know that . In order for (2.11) to reach the m level, the following equation must be satisfied:
(4.4)
So, the first passage time has the probability distribution function:
(4.5)
Figure 2. Blue graph is one possible path of the Brownian motion (2.11), red line is the m level to which it can drop. MRL: , Return process: , positive drift: , diffusion: .
If we have a Brownian motion with drift and diffusion given by:
(4.6)
and , then it is shown in [8] that the probability density function of is given by:
(4.7)
Correspondingly by [9]
(4.8)
Converting (4.7) into the terms of R yields:
(4.9)
Thus
(4.10)
The reason we switch to the bounded first passage time is that since , from (2.11) it can be shown that for . We always consider portfolio return process which has a positive drift, because we examine only long portfolios in this paper.
5. Mean-MRL-FPT Framework
After having defined the portfolio wealth process, and MRL and expectation of the bounded first passage time, we can construct the model of portfolio optimization. The goal is to find the maximum MRL and bounded First Passage Time for a given expected return for the investment end time .
So, there are three dimensions giving the efficient set of portfolios.
Varying the weights allocated in the assets gives us the set of different portfolios from which selecting the best combination of the above quantities yields the efficient surface (Figure 3).
On this surface, all risky portfolios are optimal in Mean-MRL-FPT sense since it is impossible to find a better combination of given quantities for each.
As an important note, the model is particularly useful when the individual assets within a portfolio have large variance causing the portfolio variance to be large as well. This makes the portfolio returns likely to hit the minimum level before the investment horizon. So, in this case and it makes sense to compare such portfolios. Otherwise, if the individual volatilities are low, then no matter what weights are allocated in each asset, the expected bounded first passage time frequently coincides to the investment horizon-T. In this case, for any set of weights allocated to different assets and the first passage time can be dropped altogether and the decision is to be made solely on two dimensions—Mean and Minimum Return Level. In such a situation, we would obtain the two-dimensional curve that looks much like the efficient frontier (Figure 4).
Figure 3. Surface of portfolios obtained by different weights allocated to the assets included.
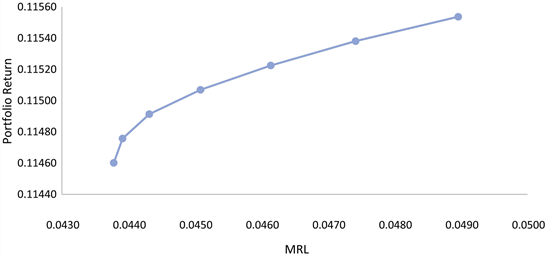
Figure 4. Efficient frontier constructed by and by different portfolios.
6. Conclusions
The paper examined the portfolio selection process by introducing the framework involving three dimensions. The basic idea was to extend the two-dimensional framework by an additional one—the expected bounded first passage time. The usefulness of the approach is evident once the individual assets within a portfolio have large volatilities causing the returns to hit the minimum level before the investment horizon. The paper only concerned itself with optimizing risky portfolios. There can be numerous continuations to the problem. If an investor decides to allocate part of the investment amount into some risk-free assets, then the optimal weights must be modified according to some criteria. In two-dimensional Mean-Variance model, maximization of Sharpe ratio and building a Capital Allocation Line (CAL) is one possible development. Similarly, one may think of capital allocation plane as an analogue to CAL in 3D. However, this paper is restricted to risky portfolio optimization.
On a final note, as far as applicability of the model is concerned, it is obviously impossible to continuously rebalance the portfolio in order to maintain the constant weights. However, one can adopt some discretization methodology to find the optimal interval for making trades and taking transaction costs into account at the same time.
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Kutalia, T. (2019) Level-Expected Bounded First Passage Time Framework. Journal of Mathematical Finance, 9, 229-238. https://doi.org/10.4236/jmf.2019.93012
References
- 1. Bookstaber, R. (1997) Global Risk Management: Are We Missing the Point? Journal of Portfolio Management, 23, 102-107. https://doi.org/10.3905/jpm.1997.102
- 2. Boudoukh, J., Richardson, M., Stanton, R. and Whitelaw, R. (2004) MaxVar: Long-Horizon Value-at-Risk in a Mark-to-Market Environment. Journal of Investment Management, 2, 14-19. https://doi.org/10.2139/ssrn.520805
- 3. Artzner, P., Delbaen, F.., Eber, J.-M. and Heath, D. (1999) Coherent Measures of Risk. Mathematical Finance, 9, 203-228. https://doi.org/10.1111/1467-9965.00068
- 4. Rockafellar, R.T. and Uryasev, S. (2000) Optimization of Conditional Value at Risk. Journal of Risk, 2, 21-41.
- 5. Chen, L., Peng, J., Zhang, B. and Rosyida, I. (2017) Diversified Models for Portfolio Selection Based on Uncertain Semi Variance. International Journal of Systems Science, 48, 637-648. https://doi.org/10.1080/00207721.2016.1206985
- 6. Qin, Z.F., Kar, S. and Zheng, H.T. (2014) Uncertain Portfolio Adjusting Modelusing Semi Absolute Deviation. Soft Computing, 20, 717-725. https://doi.org/10.1007/s00500-014-1535-y
- 7. Dana, J. (2007) Financial Markets in Continuous Times. Springer-Verlag, Berlin, Heidelberg, New York.
- 8. Shreve, S. (2008) Stochastic Calculus for Finance II. Springer Science & Business Media, New York.
- 9. Karatzas, S. (1991) Brownian Motion and Stochastic Calculus. Springer-Verlag, New York.




