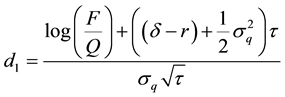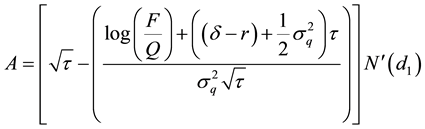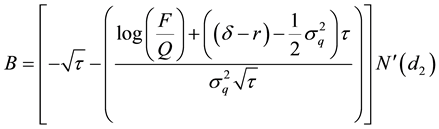Journal of Mathematical Finance
Vol.05 No.04(2015), Article ID:60899,13 pages
10.4236/jmf.2015.54027
The Role of Collateral in Credit Markets
Joseph Atta-Mensah
Capacity Development Division, United Nations Economic Commission for Africa, Addis Ababa, Ethiopia

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 9 April 2015; accepted 2 November 2015; published 5 November 2015

ABSTRACT
The author examines the role of collateral in an environment where lenders and borrowers possess identical information and similar beliefs about its future value. Using option-pricing techniques, he shows that a secured loan contract is equivalent to a regular bond and an embedded option to the borrower to default. The author finds that the lender will not advance to the borrower, a loan that exceeds the market value of the collateral, and that the supply of loans increases with a rise in the market value of the collateral. Increases in the volatility of the value of the collateral, interest rate, and dividend rate of the collateral independently depress the loan supply. The author also derives the cost of a third-party guarantee of a loan and an implied risk premium.
Keywords:
Collateral, Credit, Credit Aggregates, Option Pricing, Risk Premium

1. Introduction
Loan contracts generally require that the borrowers post assets which can be taken over by lenders if the borrowers default on the promised payments. An explanation for such contractual arrangements is that borrowers and lenders have asymmetric information about the project which the loan is financing: because the borrowers appear to know more about the project than the lender, and the borrowers’ evaluation of the project tends to be higher than that of the lenders. According to a strand of the literature, collateral in loan agreements in this environment acts as a disincentive for borrowers to default.
Another strand of the literature argues that collateral plays an important role in loan negotiations even when borrowers and lenders have the same information but differ in beliefs. In this environment, the collateral signals information to the lender about the riskiness and/or prospects of the project that the loan is needed to finance. The borrowers provide collateral as a way of sorting themselves out by risk class if lenders believe that the level of secured loan indicates the project’s profitability. Lenders may have such beliefs because the secured debt is costly for borrowers whose projects are of low quality.
The focus of this paper is to re-examine the role of collateral in a loan contract. Our approach differs from the literature in that both lenders and borrowers have the same information and identical beliefs regarding the prospects of the project. Hence, the reason for credit rationing is not the asymmetric information, a common rationale used in the literature to motivate the credit market. In our analysis, collateral can be assets used in the project or outside assets owned by the borrowers who are not part of the project. Although the initial value of the collateral is known to the transactors of the loan contract, the future value is uncertain. Both the lender and borrower agree on the probability distribution of the future value of the collateral. In addition, we show that for every secured loan contract there is an embedded option value which allows the borrower to strategically choose when to default.
This paper is organized as follows: Section 2 briefly reviews the literature on the role of collateral in loan agreements; Section 3 describes the model; Section 4 discusses the cost of a loan that is guaranteed by a third party, and derives an expression for the implied risk premium embedded in the loan contract; Concluding remarks are presented in Section 5.
2. Collateral and the Credit Markets
Along with the interest rate level, collateral plays an important role in credit markets.1 The data in the United Kingdom reveal that the value of collateral posted by small businesses exceeds the value of loans [2] . Most commercial loan agreements also require collateral as security, [3] [4] and the size of collateral impedes the creation of small businesses [2] . All these observations indicate that collateral plays an important role in the pricing of credit instruments.
There are two types of collateral. The first is called inside collateral, in which the borrower uses an asset in the project to be financed as collateral; if there is a default, the lender takes possession of the project. The second type is called outside collateral: assets not used in the project are posted as collateral.
Why do lenders demand collateral from borrowers? In the literature, asymmetric information on projects is used as a plausible explanation for the use of collateral, as well as for the existence of imperfections in the credit markets. Banks and entrepreneurs usually have divergent evaluations of projects. Entrepreneurs tend to evaluate projects more highly than creditors do. In credit markets with moral hazard or adverse selection, outside collateral serves as an incentive, or screening device, [5] [6] and [7] , and that outside collateral increases the punishment for default. It has to note that if a borrower can choose from a variety of risky projects, then collateral ensures that low-risk projects will be chosen [8] . In the case of adverse selection, lenders could offer a menu of contracts that rank loan applicants according to the riskiness of projects. In this scenario, Bester (1994) reports that the entrepreneurs with a low probability of default reveal themselves by posting the collateral which is unattractive to high-risk borrowers.
Collateral is posted by borrowers when there is asymmetric information with costly state verification [8] . This can be explained by considering a model of borrowing and lending in which an entrepreneur needs to raise capital for a risky project, the outcome of which cannot be observed by the lender. Bester shows that, within this framework, an optimal loan contract must have the commitment of the lender to impose bankruptcy and liquidate some or all of the entrepreneur’s remaining assets in the project in the event of default. The bankruptcy clause acts as a payment incentive for the entrepreneur. In other words, the lender enforces truth-telling behaviour by threatening to impose bankruptcy on the defaulting entrepreneur.
Consider the case in which the lender cannot precommit to impose bankruptcy on defaulting entrepreneurs [8] . In this case outside collateral will weaken the entrepreneurs’ incentive to default on debt payments and allow the lenders to renegotiate a larger proportion of loans, avoiding some suboptimal assets transfer. Loan agreements are renegotiated when bankruptcy is inefficient for both parties. For example, in the face of prohibitive liquidation costs, lenders are better off renegotiating the contract to prevent default. The rewriting of loan contracts, which may include partial debt forgiveness, could bring about moral hazard. Entrepreneurs, knowing that there is a chance of debt forgiveness, may opt to default even in good states of the world in an attempt to renegotiate the repayment. To discourage this behaviour, lenders could ask for outside collateral against the loan. It has to be emphasized that the larger the size of the collateral, the more inclined the lenders are to believe that the project return is low when borrowers decide to default. Lenders therefore find the option of partial debt forgiveness more profitable than taking over the project. Thus, under this framework, outside collateral helps minimize the cost of bankruptcy.
The use of collateral imposes some economic costs [8] . These costs could include legal documentation, monitoring and/or insurance costs, and the implicit costs to the borrower for being forced to relinquish discretionary use of the collateralized asset. It has to be pointed out during bankruptcy procedures; banks may incur the costs of collecting and marketing the collateralized asset [9] . Collateralized assets may be intrinsically more valuable to the borrower than the lender. For example, small businesses commonly use their own homes as collateral against bank loans. The value of the home to the borrower is generally larger than its market value. Selling the asset therefore involves a welfare loss.
It is very clear that collateral plays an important role in determining the price of a credit instrument. In section 3, we use asset-pricing techniques to formally examine the role of collateral in the valuation of a standard loan contract.
3. A Simple Model for Pricing a Loan Contract
In this section, option-pricing techniques are applied to examine the importance of collateral in the pricing of credit instruments. The use of the option pricing techniques is because of its flexibility in allowing one to gain analytical insights into the links between collateral and the credit market. The loan contract considered has the following features. A borrower takes a loan, which is secured with collateral. The loan contract is a one-time contract, where the borrower pays back the loan at an agreed date. Under the contract agreement, the lender takes possession of the collateral if the borrower defaults on the payment. It is assumed that, although the future value is unknown, the initial market value of the collateral is known to the lender and the borrower. Under this assumption, the borrower will rationally default at any time during the contract period if the market value of the collateral is less than the outstanding balance of the loan.
Under the arrangement and the assumptions of the loan contract, if the principal of the loan is F and the market value of the collateral is Q, then the expected value of the loan to the lender at the end of the contract is:
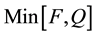 (1)
(1)
A further assumption is made that the collateral could be either inside or outside assets. Also, for simplicity, it is assumed that embedded in F are all the necessary costs incurred by the borrower upon defaulting on the loan agreement.2
In addition to the above assumption, the usual assumptions for modelling continuous-time asset-pricing models are made: 1) assets are traded in a frictionless or perfect market, where there are no taxes, transactions costs, or short sale restrictions, and all assets are perfectly divisible; 2) trading of assets is done continuously; and 3) the value of the collateral follows a continuous-time diffusion process. Interest rates are also assumed to be deterministic.3
To distinguish the model from those based on asymmetric information, it is assumed that lenders and borrowers have the same information on, and identical beliefs in, the prospects for the project. Both borrowers and lenders therefore agree on the diffusion process followed by the value of the collateral.
Thus, if Q(t) is the market value of the collateral, then its stochastic process is of the form:
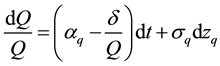 (2)
(2)
where 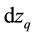 is a standard Brownian motion, with mean zero and variance dt. In Equation (2), it is assumed that the bearer of the collateral receives dividend or service flow at a constant rate,
is a standard Brownian motion, with mean zero and variance dt. In Equation (2), it is assumed that the bearer of the collateral receives dividend or service flow at a constant rate, . The borrower continues to receive the dividend until such time that they default, after which it goes to the lender. The diffusion part (the second part on the right-hand side) of Equation (2) makes the instantaneous rate of appreciation of the collateral
. The borrower continues to receive the dividend until such time that they default, after which it goes to the lender. The diffusion part (the second part on the right-hand side) of Equation (2) makes the instantaneous rate of appreciation of the collateral
uncertain. Hence, the expected rate of appreciation of the collateral is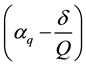 .
.
3.1. Valuation of the Loan Contract
Given the value of the collateral, Q, let the value of the secured loan at any time be L(Q, t). Then, applying Ito’s lemma, the drift and the diffusion of the loan are given as:
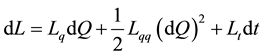 (3)
(3)
which upon simplification yields:
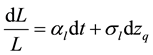 (4)
(4)
where
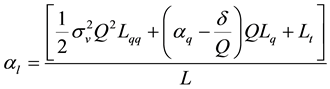 (5)
(5)
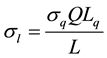 . (6)
. (6)
Proposition 1: The partial differential equation governing the loan is:
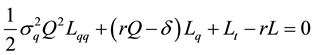 (7)
(7)
Proof:
Using standard arbitrage arguments common in the options-pricing literature, consider forming a portfolio, the value of which is H, by investing ω in the collateral asset and 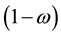 in the loan. The instantaneous return on such a loan, dH, is:
in the loan. The instantaneous return on such a loan, dH, is:
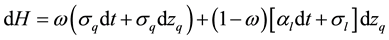 (8)
(8)
Rearranging,
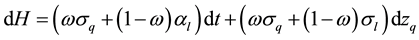 (9)
(9)
The risk of H can be hedged away if ω is selected to satisfy:
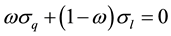 (10)
(10)
implying that
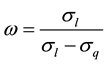 . (11)
. (11)
An investment position of 
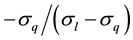
be riskless. For there to be no arbitrage profits, the instantaneous return on the portfolio must be equal to that of a risk-free asset, r.
Thus:
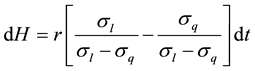
Equating Equation (12) with the drift term of Equation (9), with the substitution of ω, we have:

Substituting Equation (5) and Equation (6) into Equation (13) and rearranging yields the differential equation that governs the loan contract (Equation (7)).
An intuitive explanation in the finance literature for the differential equation that summarizes the loan contract is as follows. The first term on the left-hand side of Equation (7) captures Jensen’s inequality effect coming from the variance of the value of the collateral. The second term represents the risk-adjusted expected drift of the value of the collateral. The third term reflects the shrinking time-to-maturity. The last term represents the net flows to the lender.
Proposition 2: Under the set of assumptions given earlier, the value of the loan is:
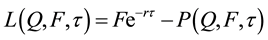
where 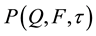
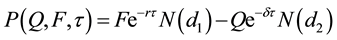
where
and N(.) is the cumulative normal distribution function.
Proof:
Begin by rewriting Equation (1) as:

Under the set of assumptions given earlier, Equation (16) suggests that the value of the loan is equivalent to a regular bond (having a face value of F and no coupon payments) and a short position on a European put option on the collateral, with the time left to maturity τ (T − t) and the strike price equal to the final payment of the loan, which by our assumption is the principal, F. The first term of Equation (14) corresponds to the present value of a bond. The put value option follows from [10] [11] , and [12] . Lastly, by performing the relevant differentiations, Equation (14) and Equation (15) correspond to Equation (7), the stochastic partial differential.
From propositions 1 and 2, it is observed that the value of the collateral plays an important role in the evaluation of loan contracts. Proposition 2 clearly shows that the value of the loan is a function of the value of the collateral. Section 3.2 examines how the underlying parameters of the model affect the supply of credit.
3.2. Factors Influencing the Supply of Credit
In this section, an attempt is made to enhance the understanding of the factors that affect the terms and conditions of credit, and the possible role those factors play in the propagation of the business cycle.
Proposition 3: The supply of loans will rise with the increase in the value of collateral.
Proof:
Differentiating Equation (14) with respect to Q and using Equation (A10) in Appendix A:
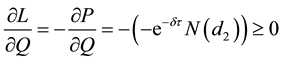
Remarks: The result corroborates conventional wisdom, which suggests that the higher the value of the collateral, the greater the size of the loan, given the same level of project risk. Furthermore, if net worth is a proxy for collateral, then the result supports the view that firms face a credit squeeze when their net worth falls in value. Moreover, the more valuable the collateral, the less chance the borrower will default on the loan, since the option value falls with the rise in the value of the collateral.
Proposition 4: The supply of loans falls as the value of the collateral becomes more volatile.
Proof:
Differentiating Equation (14) with respect to the variance of Q, and using Equation (A16) in Appendix A:
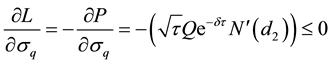
Remarks: The result demonstrates that lenders are less inclined to give out loans that are secured with very volatile collateral. The increase in the volatility of the collateral’s value increases the value of the put option attached to the loan, because a put call has no downside risk, since the value of the put is zero irrespective of how far it finishes out of the money. Hence, an increase in the volatility of the collateral increases the chances that the put option will expire in the money. The rise in the value of the collateral, following the increase in the volatility of the collateral, also increases the chances of loan default. This explains why certain intermediaries will not accept securities as collateral.
Proposition 5: The supply of loans is an increasing function of the principal, F.
Proof:
Differentiating Equation (14) with respect to F and using Equation (A21) in Appendix A:
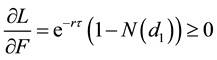
since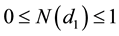
Remarks: Proposition 5 needs no further explanation, because one would intuitively expect the supply of loans to rise with the rise in the principal value.
Proposition 6: A tightening of monetary policy has a negative impact on the supply of loans.
Proof:
Differentiating Equation (14) with respect to the interest rate, r, and using Equation (A24):

since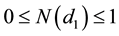
Remarks: The result shows that the raising of interest rates leads to a fall in the supply of loans. The rationale behind this result is that the rise in interest rates reduces the present values of the bond component of the loan and the exercise price of the put option, combining to depress the loan supply. The results may also explain why central banks tend to lower interest rates when the terms and conditions for borrowing are tight, especially during a downturn of the business cycle.
Proposition 7: The rise in the dividend rate on the collateral has an adverse effect on the supply of loans.
Proof:
Differentiating Equation (14) with respect to the dividend rate, d, and using Equation (A26):

Remarks: An intuitive explanation of this result is that the rise in the dividend rate enhances the value of the put option. With the value of the put option rising, the chance of default also goes up, leading the lenders to cut back the supply of loans.
Proposition 8: The term-to-maturity date has an ambiguous effect on the supply of loans.
Proof:
Differentiating Equation (14) with respect to the term left to maturity, τ, and using Equation (A33):
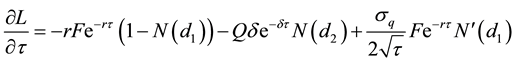
Clearly, the sign for Equation (22) is indeterminate.
Remarks: This result indicates that lenders are indifferent between offering short- and long-term loan contracts.
Proposition 9: The maximum size of a loan the lender will advance to the borrower will not exceed the value of the collateral. Thus:
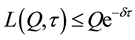
Proof:
Taking the limit of L(.) in Equation (14) as r → ∞ gives the result. Note that if the collateral yields no dividends (or δ = 0), then the maximum amount of loan offered is Q.
Remarks: The results state that a rational lender will advance to a borrower an amount not exceeding the market value of the collateral. This places a ceiling on the loan supply. For example, a borrower that holds the collateral that pays a dividend rate of 20 per cent per year, and needs a loan that matures in 10 years, will receive from a rational lender a maximum 14 per cent of the current market value of the collateral, no matter how high an interest rate the borrower is prepared to pay.
4. Loan Guarantee and Risk Premium
In section 3, an expression is derived for the valuation of a loan contract secured with collateral. The impact of a third party that guarantees to pay the lender should the borrower default is also examined. In addition, an expression is derived for the implied risk premium embedded in the loan contract.
4.1. The Cost of a Loan Guarantee
Consider a case in which there is a third party that guarantees to pay the lender should the borrower default.4 This contract, between the borrower and the guarantor, would require that the borrower surrender the collateral to the guarantor in the event of a loan default. Note that the collateral could be the assets of the borrower or the value of the project being financed with the loan.
Before the pricing formula for the cost of the guarantee is derived, the pay-offs under various states of the world is analyzed. On the maturity date of the loan, if the value of the collateral, Q, exceeds the promised payment of the loan, F, then the borrower pays the lender, F, and keeps Q − F. On the other hand, if the value of the collateral, Q, is less than the promised payment of the loan, F, the third party pays the lender F and takes a loss of F − Q, with the borrower receiving nothing.
Proposition 10: The cost of the loan guarantee is equivalent to a European put option, the underlying asset of which is Q and the exercise price F.
Proof:
The contractual arrangement suggests that, at the maturity date, the lender will receive the promised payment, F, regardless of the state of the world. Thus, to the lender the loan is riskless. The net receipt for the borrower is max (0, Q − F), with or without a guarantee. The net receipt to the guarantor is min (0, Q − F), which is non-positive. As a result of the guarantee, the borrower receives an additional cash inflow of ?min (0, Q − F), or max (0, F − Q). Hence, if G(τ) is the value of the guarantee to the borrower, then
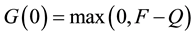
which is equivalent to a put option. Equation (15) gives the exact formula for evaluating the option.
4.2. Risk Premium
In this section, an expression is derived for the risk premium embedded in the loan contract. To a lender, a loan that is guaranteed by the borrower is riskless. The difference between the yield on a loan that is not guaranteed and one that is guaranteed is a measure of the risk premium.
Proposition 11: The risk premium embedded in a loan contract is a function of the ratio of the cost of the loan guarantee and the present value of the promised payment.
Proof:
Let y(τ) be the implied yield of the debt, F, when there is no guarantee, implying that the present value of the debt is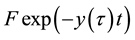
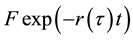
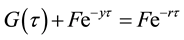
from which the implied risk premium is derived as:
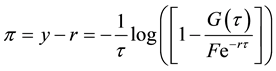
Equation (26) gives an expression for the implied risk premium.
Factors Influencing the Risk Premium
In section 3, it was shown that the value of the collateral plays an important part in the determination of a loan contract. This section examines factors that influence the risk premium.
Proposition 12: The risk premium is negatively correlated with the value of the collateral.
Proof:
Differentiate Equation (26) with respect to Q:
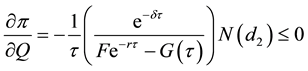
since 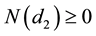
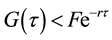
Remarks: An explanation for this result is that an appreciation in the value of the collateral leads to a lesser chance of the borrower defaulting on the promised payment of the loan. The risk premium falls, reflecting the reduced risk of default.
Proposition 13: The risk premium rises as the value of the collateral becomes more volatile.
Proof:
Differentiate Equation (26) with respect to σq:
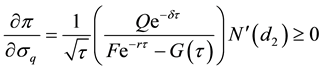
since 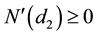
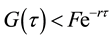
Remarks: An increase in the volatility of the value of the collateral increases the option-value component of the loan. Consequently, the risk of default by the borrower rises, resulting in the rise in the risk premium.
Proposition 14: The impact of monetary policy on the risk premium is indeterminate.
Proof:
Differentiate Equation (26) with respect to r:

Remarks: The results indicate that the impact of monetary policy on the risk premium is indeterminate. A common view held by market analysts is that an expansionary monetary policy will help reduce risky spreads. Our result, however, indicates that the impact of monetary policy on the risky spread cannot be ascertained.
5. Conclusions
This paper examines the role of collateral in an environment where lenders and borrowers possess identical information and similar beliefs about its future value. Two views in the literature have been brought together: one argues that collateral is needed in loan contracts because of the asymmetric information between the lender and borrower, and the second examines the role of collateral in an environment where lenders and borrowers have identical information but different beliefs about the future value of the collateral.
Using option-pricing techniques, the paper shows that a secured loan contract is equivalent to a regular bond and an embedded option to the borrower to default. The results show that the lender will not advance to the borrower if a loan exceeds the market value of the collateral. In addition, the paper finds that the supply of loans increases with a rise in the market value of the collateral. Increases in the volatility of the value of the collateral, interest rate, and dividend rate of the collateral independently depress the loan supply. The paper also derives the cost of a third-party guarantee of a loan and an implied risk premium.
Acknowledgements
The author acknowledges the useful comments of David Bolder, Céline Gauthier, Jack Selody, and Greg Tkacz, all former colleagues at the Bank of Canada, Prof. Robert Jones of Simon Fraser University and colleagues at the Economic Commission for Africa. However, any errors or omissions must be attributed to the author. Of course, the views expressed in this paper are those of the authors and should not be attributed to the United Nations.
Cite this paper
JosephAtta-Mensah, (2015) The Role of Collateral in Credit Markets. Journal of Mathematical Finance,05,315-327. doi: 10.4236/jmf.2015.54027
References
- 1. Coco, G. (2000) On the Use of Collateral. Journal of Economic Surveys, 14, 191-214.
http://dx.doi.org/10.1111/1467-6419.00109 - 2. Black, J., de Meza, D. and Jeffreys, D. (1996) House Prices, the Supply of Collateral and the Enterprise Economy. The Economic Journal, 106, 60-75.
http://dx.doi.org/10.2307/2234931 - 3. Leeth, J. and Scott, J. (1989) The Incidence of Secured Debt: Evidence from the Small Business Community. Journal of Financial and Quantitative Analysis, 24, 379-394.
http://dx.doi.org/10.2307/2330818 - 4. Berger, A. and Udell, G. (1990) Collateral, Loan Equity, and Bank Risk. Journal of Monetary Economics, 25, 21-42.
http://dx.doi.org/10.1016/0304-3932(90)90042-3 - 5. Bester, H. (1985) Screening vs. Rationing in Credit Markets with Imperfect Information. American Economic Review, 75, 850-855.
- 6. Besanko, D. and Thakor, A. (1987) Competitive Equilibrium in the Credit Market under Asymmetric Information. Journal of Economic Theory, 42, 167-182.
http://dx.doi.org/10.1016/0022-0531(87)90108-6 - 7. Chan, Y. and Kanatas, G. (1985) Asymmetric Valuation and the Role of Collateral in Loan Agreements. Journal of Money, Credit and Banking, 17, 84-95.
http://dx.doi.org/10.2307/1992508 - 8. Bester, H. (1994) The Role of Collateral in a Model of Debt Renegotiation. Journal of Money, Credit and Banking, 26, 72-86.
http://dx.doi.org/10.2307/2078035 - 9. Barro, R. (1976) The Loan Market, Collateral and Rate of Interest. Journal of Money, Credit and Banking, 8, 839-856.
http://dx.doi.org/10.2307/1991690 - 10. Atta-Mensah, J. (1992) The Valuation of Commodity-Linked Bonds. Unpublished PhD Thesis, Simon Fraser University.
- 11. Merton, R. (1973) The Theory of Rational Option Pricing. Bell Journal of Economics and Management Science, 4, 141-183.
http://dx.doi.org/10.2307/3003143 - 12. Geske, R. (1979) The Valuation of Compound Options. Journal of Financial Economics, 7, 63-81.
http://dx.doi.org/10.1016/0304-405X(79)90022-9 - 13. Merton, R. (1977) An Analytical Derivation of the Cost of Deposit Insurance and Loan Guarantees: An Application of Modern Option Pricing Theory. Journal of Banking and Finance, 1, 3-11.
http://dx.doi.org/10.1016/0378-4266(77)90015-2
Appendix A: Properties of the Put Option
A1. The Value of the Put Option
In the main text, an expression is derived for valuing a European put option as:
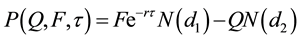
where
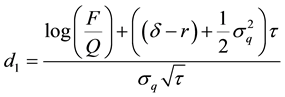

and N(.) is the cumulative normal distribution function.
The paper now turns to the sensitivity of the value of the put to the parameters.
A2. The Change of the Price of the Collateral on the Put Option
Differentiate the put with respect to the collateral price, Q:
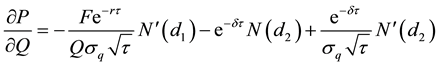
but
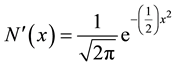
thus
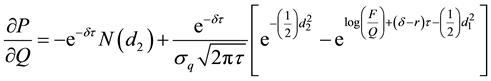
Substitute Equation (A2) and Equation (A3) in the last part of Equation (A6):
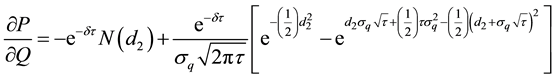
which simplifies into:
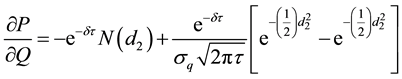
or:
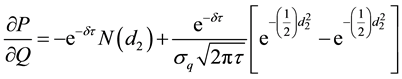
Hence:
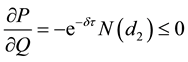
A3. The Change of the Variance of the Price of the Collateral on the Put Option Value
Differentiate the put price with respect to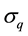
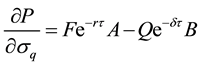
where
and
Simplifying,

Further,
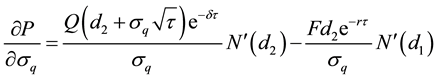
or

Furthermore,
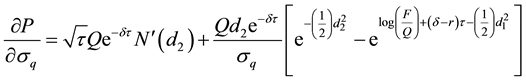
As previously shown, the term in the square bracket on the right-hand side of Equation (A15) reduces to zero. This implies that:
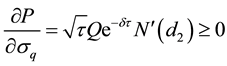
A4. The Change of the Principal on the Put Option Value
Differentiate the put option value with respect to F:
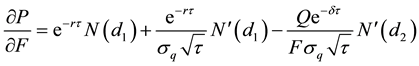
which could be expressed as:
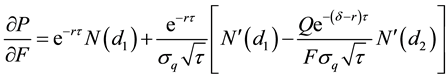
Manipulating further:
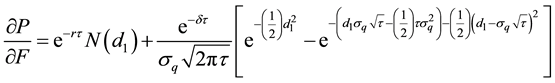
which reduces to:
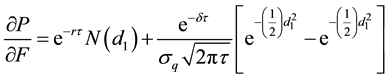
Hence,
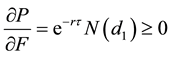
A5. The Change of the Interest Rate on the Put Option Value
Differentiate with respect to r:
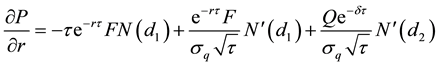
Simplifying,
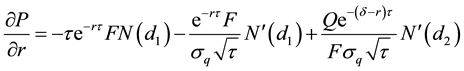
From the previous section, the second term on the right-hand side is zero. Hence,
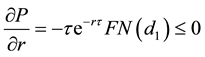
A6. The Change of the Dividend Rate on the Put Option Value
Differentiate with respect to δ:

Following the previous sections, it can easily be shown that:
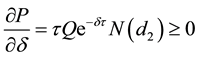
A7. The Change of the Term to Maturity on the Put Option Value
Differentiate with respect to τ:
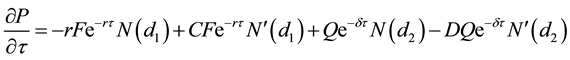
where
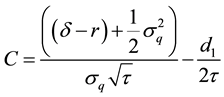
and
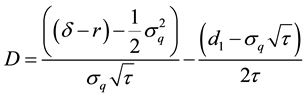
Substituting C and D and manipulating further:
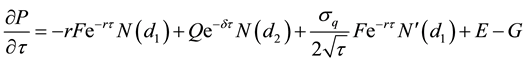
where
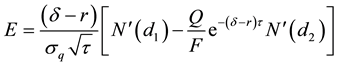
and
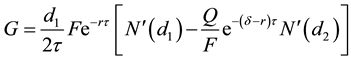
With the terms in the square brackets in A(31) and A(32) equal to zero,
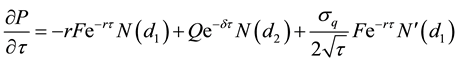
Clearly, the sign of Equation (A33) is indeterminate.
NOTES
1See [1] on a detailed discussion of the subject.
2These costs may include bankruptcy, legal, and reputation costs.
3This assumption is very restrictive. Incorporating a stochastic interest rate into the model, however, complicates the analysis without changing the results.
4The discussion in this section is based on [13] .