Journal of Mathematical Finance
Vol.05 No.01(2015), Article ID:53355,13 pages
10.4236/jmf.2015.51001
Optimal Execution in Illiquid Market with the Absence of Price Manipulation
Seiya Kuno1, Masamitsu Ohnishi2
1Center for the Study of Finance and Insurance, Osaka University, Osaka, Japan
2Graduate School of Economics, Osaka University, Osaka, Japan
Email: kuno@sigmath.es.osaka-u.ac.jp, ohnishi@econ.osaka-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 December 2014; accepted 16 January 2015; published 20 January 2015
ABSTRACT
This article shows the execution performance of the risk-averse institutional trader with constant absolute risk aversion (CARA) type utility by using the condition of no price manipulation defined in the risk neutral sense. From two linear price impact models both satisfying that condition, we have derived the unique explicit optimal execution strategy calculated backwardly with dynamic programming equations. And our study shows that the optimal execution strategy exists in the static class. The derived solution can be decomposed into mainly two components, each giving an explanation of the property of optimal execution volume. Moreover we propose two conditions in order to compare the performance of these two price models, and illustrate that the performances of the two models are surprisingly different under certain conditions.
Keywords:
Optimal Execution, Price Manipulation, Algorithmic Trading

1. Introduction
In the competitive market paradigm, it is assumed that security markets are perfectly elastic and all orders can be executed instantaneously. However in real markets, since institutional traders (large traders) usually submit orders of considerable sizes, such traders thus influence the price by their own dealings (called market (price) impact) and create the execution time lag for their orders. Thus the large trader often divides her holdings (orders) into small pieces considering the tradeoff between market impact risk due to her fast execution and volatility risk due to her slow execution. In [1] , such a price change (price impact) occurring at each trading period can be divided into three components. Firstly a temporary impact which represents the temporary cost of demanding liquidity and only affects an individual trade, and secondly a transient impact which represents gradual incorporation of trade information to the price which derives the gradual price recovery, and finally a permanent impact which affects the prices of all subsequent trades of an agent. These price changes may enable the large trader to manipulate the market. The act of manipulating the market intentionally and through managed actions to make profits actively spoils market public welfare, and is forbidden in many trading venues. With the appearance of electronic trading, this problem got more concerns in financial literature. In optimal execution literature many studies are often conducted as the following way. Firstly, the price process model that considers such a price change under the condition of no price manipulation is built; then, the optimization problem with such a price model in the static or dynamic way in the discrete or continuous time setting is solved.
In this paper, under no price manipulation condition, we consider mainly two types of price model depending on how the price is reverted to its previous price level for the buy trade. Let’s call one of them the permanent (impact) price model (as in e.g. [2] and [3] ) and the other the transient (impact) price model (as in e.g. [4] and [5] ). In the permanent price model, the execution price that lifted up by the large trader’s order immediately reverts to a permanent level which is usually higher than the price at the previous trading time. On the other hand, the transient price model considers the price that reverts to a permanent level gradually in time. That is, one of the differences between the two models is whether the temporary impact decays instantly (in the permanent price model) or gradually (in the transient price model). A large number of empirical studies have been reported for the basis of the transient price model in various trading venue, refer to e.g. [6] and references therein. Although many empirical studies also show the non-linearity of the price impact function, we use the linear one for simplicity of calculation.
The main goal of this paper is to derive the optimal execution strategies for these two price models. Then in the equidistance discrete trading time grid setting, we show that the optimal execution strategy of the risk-averse large trader with each price model exists in the static class by deriving backwardly the explicit solution with the dynamic programming equation. This result is similar to the one found in [7] which derives the optimal execution strategy dynamically with the continuous time permanent price model, but our approach with the discrete time transient price model can decompose the optimal solution into various components and then gives the intuitive interpretation about the existence of price manipulation. Moreover, since we found that there exist the optimal execution strategies for two price models in the static class, it can be easy to compare the cost performance by simulations and parameter settings between the price models.
The rest of the paper is organized as follows. In Section 2, we present two price dynamics and two definitions of the price manipulation. In Section 3, we describe the optimization problem and derive explicit solutions for the two price models. Furthermore, we show the property of the optimal execution strategy and illustrate it using the comparative statics. In Section 4, we consider the relationship between two price models. The transient price model is more realistic but a little bit complicated therefore it takes much time when we simulate the execution performance, on the other hand the permanent price model is unrealistic but simple enough to be able to make high-speed trading decision in algorithmic trading system. For that reason, we suggest how to incorporate the intrinsic parameter of the transient price model into the permanent price model. More concretely, we propose two conditions that exist between those two price models under the TWAP (Time Weighted Average Price) strategy, when we attempt to compare the performance of those two price model in the same market. Section 5 contains a conclusion. Calculations and proofs are complicated but can be proved in a straightforward way.
2. Market Models and Price Manipulation
In this section, we explain two existing price models in the discrete time setting. One is the permanent impact (price) model proposed by [3] , which extends to that of [8] and another is the transient impact (price) model proposed by [4] , which is a generalization of that of [5] . A risk-averse institutional trader (after that we call her a large trader in the sense that she submits large order volumes) and many noise traders also called liquidity providers are considered as economic agents. The superscript of each variable denoting i = pe or tr represents the use of the permanent price model or transient price model respectively. Through this paper, we set the exponential decay of the temporary impact in the transient price model, because it satisfies the no price manipulation according to Definition 2 stated later in this section.
2.1. Two Price Models
Suppose that 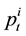 is the price of a single risky asset at time t,
is the price of a single risky asset at time t,  is the large trader’s execution volume. If
is the large trader’s execution volume. If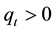 , it is the buy trade, on the other hand if
, it is the buy trade, on the other hand if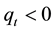 , it is the sell trade.
, it is the sell trade.  is the number of shares which the large trader remains to purchase, if
is the number of shares which the large trader remains to purchase, if  (or liquidate, if
(or liquidate, if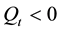 ). That is,
). That is,
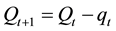 (1)
(1)
Moreover, 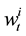 is the investment capital (wealth). For simplicity, we assume in the following that the large trader plans to purchase the asset. If at time t, the large trader submits large amount of her market order
is the investment capital (wealth). For simplicity, we assume in the following that the large trader plans to purchase the asset. If at time t, the large trader submits large amount of her market order 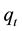 just after she has recognized the price at that time
just after she has recognized the price at that time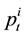 , the order is executed immediately. However, the execution price may not be equal to
, the order is executed immediately. However, the execution price may not be equal to . The execution price will be instantly lifted upward from
. The execution price will be instantly lifted upward from 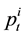 to
to 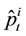 because of the temporary imbalance of supply and demand. Assume that
because of the temporary imbalance of supply and demand. Assume that 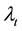 denotes the price change per share (called price impact), the dynamics of
denotes the price change per share (called price impact), the dynamics of 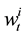 and
and 


The lifted price by the large order reverts to the previous price level to a certain extent.
In the permanent price model, the execution price diminishes instantly to the permanent impact level and the expected price is maintained until the next trading time. That is,

Using Equation (3) and (4),

where 





All information available to the large trader before her trading at time t are

In the permanent price model, the price impact, the temporary impact and the permanent impact are repre- sented respectively by


The transient price model, on the other hand, is the same as the permanent price model until the submitted order is executed. However the price reversion toa permanent level is not immediate but gradual. We set the time independent rate 

where 


Here, we define S as

where

In this transient price model, the price impact and the transient impact are 

Remark 1: The economic interpretation of 

The reason why we use these specific two price models is its viability, as it will explained in the next subsection. The main difference between these two models is whether the effect of the present execution is completely incorporated in the price immediately or not. In the transient price model, since the price after the present execution fall down gradually to the permanent level (in this case 0), the effect of the present execution is partially incorporated in the price at the following trading time, and is completely incorporated after a certain period.
2.2. Absence of Price Manipulation
In this subsection, we introduce the concept of price manipulation from the perspective of the feasibility of the price model. This is because the market can easily crash with the price manipulation of the large traders in the current market environment where the high-frequency trading is becoming a main stream. So the construction of the feasible price model is essential to limit such a price manipulation. In the following we introduce two concepts of price manipulation.
Definition 1 ((Pure) Price manipulation [9] ): A round trip trade is an execution strategy 


It is shown in [9] that if the permanent impact is linear in terms of execution volume, then the pure price manipulation is absent from the market in the risk neutral sense. Within the time-homogeneous reversion rate framework, our permanent price model satisfies this condition.
Definition 2 (Transaction-triggered price manipulation [1] ): If the expected execution costs of a buy program can be decreased by intermediate sell trade, the price model admits transaction-triggered price manipulation. That is, there exists



Definition 2 states a stronger condition of the price manipulation than the one given by Definition 1. That is to say, even if the price model satisfies the absence of pure price manipulation, it may not satisfy the absence of the transaction-triggered price manipulation, such as buy and sell oscillation trades.
In this paper, we use an exponential resilience for the transient price model. This does not admit transaction- triggered price manipulation. As shown below in Remark 2, our control for the risk-averse large trader describes that when we apply the round trip trade. 0 trade is always optimal. So, both price models satisfy the condition of the absence of pure price manipulation.
3. Optimal Execution
In this section, we show that the optimal execution strategy exists in the static class by deriving the explicit solution with a dynamic programming equation. Suppose that a risk-averse large trader with CARA (Constant Absolute Risk Aversion) type utility of which the risk aversion coefficient is R submits large amount of market orders in equally time intervals over the maturity T. We consider the problem of the dynamic execution strategy that maximizes the large trader’s expected utility from her terminal wealth. Here, we show the optimal execution strategy based mainly on the transient price model. For the permanent price model, we only provide the result since it requires simpler calculation.
3.1. Execution Strategy for a Risk-Averse Large Trader
In this case, we define the large trader’s expected utility under the trading strategy 

where 

where the subscript t of the expectation represents the condition where all the information up to time t is available to the large trader.
Because of the Markov property of the dynamics and path independency of the large trader’s utility at the final period, 


We derive the sequence of the optimal execution volumes which attains 
Theorem (Optimal Execution Strategy with the Transient Price Model): When we use the transient price model, the optimal execution volume of a large trader at time t denoted 


and

where we set



Then a deterministic execution strategy becomes optimal.
Secondary, we provide the optimal execution strategy for the permanent price model as following corollary.
Corollary (Optimal Execution Strategy with permanent Price Model):
When we use the permanent price model, the optimal execution volume of a large trader at time t denoted 


and

where



We provide a short proof of this Theorem in the appendix. For the proof of the Corollary, refer to [10] . The optimal solution for the transient price model consists of two components, 







Remark 2: For both price models, 







and for the permanent price model

3.2. Properties of the Optimal Execution Strategy under Time-Homogeneous Parameter
The purpose of this subsection is to give an intuitive and intelligible analysis of the optimal strategies mainly for the permanent price model as it is difficult to give an analytical proof for the optimal execution strategy using transient price model. However we can show this intuition and confirm it using some numerical examples. To this end, we set some time-homogeneity assumptions for the impact





Lemma 1 (Monotone Decrease Property): If 


For the proof of Lemma1, refer to [7] . From Lemma 1 the strategy for the permanent price model also satisfies the absence of transaction triggered price manipulation. Therefore,

Proposition 1(Risk Aversion Effect): Suppose 



If
Proposition 2 (Risk Neutral Trader): Suppose


Moreover, for the transient price model, the optimal execution strategy is time symmetric. Then we form the following property,

Remark 3: The optimal execution strategy for the transient price model does not have the monotone decrease property (Lemma 1). However from the numerical experiment shown in Figure 1, the convexity of the optimal execution volume in time can be confirmed for both price models. Moreover, we will also find that,
However, there is analytical difficulty for the proof of this property because the terms of 

Figure 1. Optimal execution strategies for the permanent price model (upper half) and transient price model (lower half).
mutually on each other over time. In fact, when we express the optimal execution volume at time t + 1 with the states at time t,

Figure 2 shows the relationship between 

Under the time-homogeneity of


4. Comparison of Two Price Models
So far, we considered two price models, the permanent and the transient with intrinsic parameter 

Figure 2. The optimal value of two components for the transient price model.
For the two price models describing a real market, if the expected costs derived from these two price models respectively with the same execution volume at the same intervals are different from each other, an arbitrage opportunity may occur between these two models. We should then unify how the information after each trade is incorporated into the price, when we compare the performance of the two price models. So, in order to standardize the market, we should find the relationship between 




Suppose that the expected cost using TWAP strategy over the maturity T with the permanent and the transient price model are respectively

Definition 3 (TWAP Cost Equivalent): If
However, this condition does not satisfy the law of indifference which is a fundamental economic principle. As a stronger condition, we define TWAP equivalent condition as below.
Definition 4 (TWAP Equivalent): If
We can afterward derive following conditions using Equations (3), (5), (9), (10), and letting q = constant in order to adapt the transient price model according to the permanent price model.
Condition 1: If the market is TWAP cost equivalent, then the following condition holds:

Condition 2: If the market is TWAP equivalent, then the following condition holds:

The upper (lower) half of Figure 3 shows that the value of 


The calculations of these conditions are straightforward. Within Condition 1, the mean of the accumulated transient impact at each time using the transient price model is regarded as the permanent impact, and then is assigned equally to
Figure 3. The value of α for TWAP cost equivalent (upper half) and TWAP equivalent (lower half).
Figure 4. Optimal execution for TWAP cost equivalent (upper half) and TWAP equivalent (lower half).
averse large trader corresponding to the value of 





Remark 4: When 
Therefore the optimal execution strategy for the transient price model is the same as the permanent price model one with
5. Conclusion
In a discrete time setting, we derived an explicit solution for the two price models by solving a dynamic programming equation backwardly from the maturity time. Under the assumptions of a large trader with CARA utility type and public news effects on price modeled as normal random variables, the optimal execution strategy exists in the static class. In particular, since the optimal execution volume for the transient price model consists of two components, that is tradeoff between impact risk and volatility risk, and the expectation of the price reversion, that solution gives consideration to the existence of transaction-triggered price manipulation. From the comparative statics, we also illustrated how the large trader’s risk aversion affects the optimal execution strategy. Furthermore, with TWAP strategy we compared the performances of the two price models where the time-ho- mogeneity of the parameters α and ρ plays a significant role in the absence of price manipulation. But it is impossible to capture completely the essence of the price process with parameters using in this study. In recent years, an order driven market becomes mainstream in various trading venues around the world. Therefore, we should specify the shape of limit order book endogenously or exogenously in order to construct the price model. Further research consists on creating more practical models that takes for instance into consideration the intraday liquidity effect among other effects and the nonlinear impact function as empirically stated in [6] , [12] , and [13] .
Acknowledgements
The authors would like to thank participants of the International Conference on Industrial Engineering Theory, Applications and Practice (IJIE2013) at Pusan National University, the RIMS Workshop on Theory and Application of Mathematical Decision Making under Uncertainty 2013 at Kyoto University, and the Symposium on Stochastic Models 2014 at Tokyo University of Science for their constructive comments.
References
- Alfonsi, A., Schied, A. and Slynko, A. (2012) Order Book Resilience, Price Manipulation, and the Positive Portfolio Problem. SIAM Journal on Financial Mathematics, 3, 511-533.http://dx.doi.org/10.1137/110822098
- Almgren, R. and Chriss, N. (2000) Optimal Execution of Portfolio Transactions. Journal of Risk, 3, 5-39.
- Huberman, G. and Stanzl, W. (2005) Optimal Liquidity Trading. Review of Finance, 9, 165-200. http://dx.doi.org/10.1007/s10679-005-7591-5
- Gatheral, J. (2010) No-Dynamic-Arbitrage and Market Impact. Quantitative Finance, 10,749-759. http://dx.doi.org/10.1080/14697680903373692
- Obizhaeva, A. and Wang, J. (2013) Optimal Trading Strategy and Supply/Demand Dynamics. Journal of Financial Markets, 16, 1-32. http://dx.doi.org/10.1016/j.finmar.2012.09.001
- Bouchaud, J.-P., Farmer, J.D. and Lillo, F. (2009) How Markets Slowly Digest Changes in Supply and Demand. Handbook of Financial Markets: Dynamics and Evolution, Elsevier, Berlin.
- Schied, A., Schöneborn, T. and Teharanci, M. (2010) Optimal Basket Liquidation for CARA Investors Is Deterministic. Applied Mathematical Finance, 17, 471-489. http://dx.doi.org/10.1080/13504860903565050
- Bertsimas, D. and Lo, A. (1998) Optimal Control of Execution Costs. Journal of Financial Markets, 1, 1-50. http://dx.doi.org/10.1137/S0363012995291609
- Huberman, G. and Stanzl, W. (2004) Price Manipulation and Quasi-Arbitrage. Econometrica, 74, 1247-1275. http://dx.doi.org/10.1111/j.1468-0262.2004.00531.x
- Kunou, S. and Ohnishi, M. (2010) Optimal Execution Strategy with Price Impact. Research Institute for Mathematical Sciences (RIMS) Kokyuroku, 1645, 234-247.
- Lorenz, C. and Schied, A. (2013) Drift Dependence of Optimal Trade Execution Strategies under Transient Price Impact. Finance and Stochastics, 17, 743-770. http://dx.doi.org/10.1007/s00780-013-0211-x
- Almgren, R., Thum, C., Hauptmann, E. and Li, H. (2005) Equity Market Impact. Risk, 18, 57-62.
- Bouchaud, J.-P., M zard, M. and Potters, M. (2004) Statistical Properties of Stock Order Books: Empirical Results and Models. Quantitative Finance, 2, 251-256. http://dx.doi.org/10.1088/1469-7688/2/4/301
Appendix
Short proof of Theorem:
We can derive the optimal execution volume by backward induction from the maturity time T. For t = T, since the large trader must finish her purchases

Then,

where we define the maturity condition as

and the value function is

and we set

where A, B and K are the coefficients of


Next, for

where we use



where

and the value function is
where

Proceeding similarly for a general time t, we obtain the desired results (17), (19) with backward induction.
Proof of Proposition 1
From Lemma 1 and Remark 2, we show that if

Denote the terms which does not depend on R in 




From Remark 2, we have

Proof of Proposition 2
When

Suppose that if 

We will show for 

So,

From the assumption of Equation (45) and Equation (22), we get,
Moreover, from the assumption of Equation (45)
Then, 
Therefore, from Equation (22), 
Then, by substituting the above 
That is Equation (46).















