Journal of Mathematical Finance
Vol.04 No.04(2014), Article ID:48833,13 pages
10.4236/jmf.2014.44019
On the Order Form of the Fundamental Theorems of Asset Pricing
Christos E. Kountzakis
1Department of Mathematics, University of the Aegean, Samos, Greece 2Faculty of Mathematics―Group of Finance, University of Vienna, Vienna, Austria
Email: chr_koun@aegean.gr
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 May 2014; revised 4 June 2014; accepted 26 June 2014
ABSTRACT
In this article, we provide an order-form of the First and the Second Fundamental Theorem of Asset Pricing both in the one-period market model for a finite and infinite state-space and in the case of multi-period model for a finite state-space and a finite time-horizon. The space of the financial positions is supposed to be a Banach lattice. We also prove relevant results in the case where the space of the financial positions is not ordered by a lattice cone.
Keywords:
Strictly Positive Extension, Positive Projection, Sublattice, Complete Market, Incomplete Market

1. Some Remarks on Previous Work about the Fundamental Asset Pricing Theorems
The First Fundamental Theorem of Asset Pricing states that the absence of arbitrage for a stochastic process 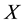 is equivalent to the existence of an equivalent martingale measure for
is equivalent to the existence of an equivalent martingale measure for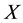 . It was shown in [1] that for a locally bounded
. It was shown in [1] that for a locally bounded 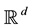 -valued semi-martingale
-valued semi-martingale 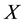 the condition of No Free Lunch with Vanishing Risk is equivalent to the existence of an equivalent local martingale measure for the process
the condition of No Free Lunch with Vanishing Risk is equivalent to the existence of an equivalent local martingale measure for the process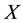 . It was proved in [2] that the local boundedness assumption on
. It was proved in [2] that the local boundedness assumption on  may be dropped under the notion of equivalent
may be dropped under the notion of equivalent 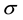 -martingale measure. The work [3] , also discussed in [4] , is still essential in this topic and actually this work’s results rely on what Kreps established as the viable market model consisted by an incomplete market and a linear price system on it. In the present work we are going to resolve the so-called Strictly Positive Extension Property from the financial aspect. The presence of heavy-tails in continuous time models and the possible change of frame from
-martingale measure. The work [3] , also discussed in [4] , is still essential in this topic and actually this work’s results rely on what Kreps established as the viable market model consisted by an incomplete market and a linear price system on it. In the present work we are going to resolve the so-called Strictly Positive Extension Property from the financial aspect. The presence of heavy-tails in continuous time models and the possible change of frame from 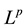 spaces to Orlicz spaces in order to fit the modelling requirements, oblige us to search for more general versions of the two FTAPs, mostly relied on the geometry of these spaces. Recently, in [5] , a Fundamental Theorem of Asset Pricing and a Super-Replication Theorem in a model-independent framework are both proposed. But these theorems are proved in the setting of finite, discrete time and a market consisting of a risky asset
spaces to Orlicz spaces in order to fit the modelling requirements, oblige us to search for more general versions of the two FTAPs, mostly relied on the geometry of these spaces. Recently, in [5] , a Fundamental Theorem of Asset Pricing and a Super-Replication Theorem in a model-independent framework are both proposed. But these theorems are proved in the setting of finite, discrete time and a market consisting of a risky asset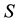 , as well as options written on this risky asset, too. Notions like the one of the strictly positive projection or that of the filtration are alike the ones met in [6] . A difference between our notion of strictly positive projection and the equivalent notion in [6] is that ours is weaker. That’s because if
, as well as options written on this risky asset, too. Notions like the one of the strictly positive projection or that of the filtration are alike the ones met in [6] . A difference between our notion of strictly positive projection and the equivalent notion in [6] is that ours is weaker. That’s because if 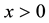 implies
implies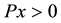 , this implies
, this implies , because if
, because if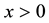 , it would be
, it would be . An important difference between the article of Troitsky and ours is that we extend the framework of Definitions so as to include cases of non-discrete time spaces. Another one is that we apply these notions in order to provide a new version of the two FTAP, while in [6] an important ordered -space theory of martingales in Banach lattices is developed. Finally, markets subspaces are taken to be sublattices because of the fact that we may include layers of call and put options written on an initial market space, as we remarked in [7] . The present paper is organized as follows: First, we provide some useful notions and definitions and examples for them, as well. Next, we prove the Order Form of the FTAP in the Banach-lattice case and in the next sections we provide the analog of these results in the finite-models case. We also explain the application of our results on the Black-Scholes-Merton model. We also compare them to the Example developed in [4] . The case of non-lattice cones is examined in the last section of the paper, in relation with the classes of reflexive and strongly reflexive cones, mentioned in [8] . The role of the existence of an unconditional basic sequence in a Banach space is also quoted in this section independently from the results provided in [8] , as an important condition for the extraction of results concerning FTAP. This condition is not irrelevant to ( [9] , Th. 1.1), about Lindelöf Properties of weak topology, but here it mainly concerns the construction of a Strictly Positive Projection Operator. On the other side, in the paper [10] ideals of
. An important difference between the article of Troitsky and ours is that we extend the framework of Definitions so as to include cases of non-discrete time spaces. Another one is that we apply these notions in order to provide a new version of the two FTAP, while in [6] an important ordered -space theory of martingales in Banach lattices is developed. Finally, markets subspaces are taken to be sublattices because of the fact that we may include layers of call and put options written on an initial market space, as we remarked in [7] . The present paper is organized as follows: First, we provide some useful notions and definitions and examples for them, as well. Next, we prove the Order Form of the FTAP in the Banach-lattice case and in the next sections we provide the analog of these results in the finite-models case. We also explain the application of our results on the Black-Scholes-Merton model. We also compare them to the Example developed in [4] . The case of non-lattice cones is examined in the last section of the paper, in relation with the classes of reflexive and strongly reflexive cones, mentioned in [8] . The role of the existence of an unconditional basic sequence in a Banach space is also quoted in this section independently from the results provided in [8] , as an important condition for the extraction of results concerning FTAP. This condition is not irrelevant to ( [9] , Th. 1.1), about Lindelöf Properties of weak topology, but here it mainly concerns the construction of a Strictly Positive Projection Operator. On the other side, in the paper [10] ideals of 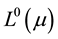 are used in order to deduce an FTAP-like result ( [10] , Lem. 1), while our results refer to sublattices.
are used in order to deduce an FTAP-like result ( [10] , Lem. 1), while our results refer to sublattices.
2. Useful Notions and Preliminaries
We consider two periods of time (0 and 1) and a non-empty set of states of the world 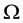 which is supposed to be an infinite set. The true state
which is supposed to be an infinite set. The true state ![]() that the investors face is contained in some
that the investors face is contained in some![]() , where
, where ![]() is some σ-algebra of subsets of Ω which gives the information about the states that may occur at time-period 1. A financial position is a
is some σ-algebra of subsets of Ω which gives the information about the states that may occur at time-period 1. A financial position is a ![]() -measurable random variable
-measurable random variable![]() . This random variable is the profile of this position at time-period 1. We suppose that the probability of any state of the world to occur is given by a probability measure
. This random variable is the profile of this position at time-period 1. We suppose that the probability of any state of the world to occur is given by a probability measure![]() . The financial positions are supposed to lie in some subspace
. The financial positions are supposed to lie in some subspace ![]() of
of![]() , being a Banach lattice.
, being a Banach lattice.
Definition 1 An incomplete market in ![]() is some sublattice
is some sublattice ![]() of
of![]() . A complete market in
. A complete market in ![]() is some sublattice
is some sublattice ![]() of
of![]() , such that
, such that![]() .
.
It is well-known that we define the positive cone ![]() of a subspace
of a subspace ![]() of an ordered vector space to be the set
of an ordered vector space to be the set![]() , where
, where ![]() denotes the positive cone of
denotes the positive cone of![]() .
.
Definition 2 A positive projection ![]() is a projection, which maps each element of
is a projection, which maps each element of ![]() to some ele- ment of its subspace
to some ele- ment of its subspace![]() , such that
, such that![]() . A positive projection is called strictly positive, if
. A positive projection is called strictly positive, if ![]()
![]() .
.
We also recall the notion of random field.
Definition 3 A random field is a map ![]() where
where ![]() is a Bananch lattice,,
is a Bananch lattice,, ![]() is a topological space and
is a topological space and![]() , for any
, for any![]() . Such a random field
. Such a random field ![]() is called associated to the pair
is called associated to the pair![]() .
.
We also may provide the notion of the filtration in the frame of random fields:
Definition 4 A filtration associated to the pair ![]() is a net of projections
is a net of projections![]() , where
, where![]() , where
, where ![]() is a sublattice of E and if
is a sublattice of E and if![]() . A is a directed set, by some binary relation
. A is a directed set, by some binary relation![]() , called direction.
, called direction.
Definition 5 A binary relation ![]() on A is called direction on A, if it is reflexive and transitive on A, while for any
on A is called direction on A, if it is reflexive and transitive on A, while for any ![]() there is a
there is a![]() , such that
, such that![]() .
.
Definition 6 If ![]() and
and![]() , this is denoted by
, this is denoted by![]() .
.
Definition 7 A filtration ![]() is called strictly positive if
is called strictly positive if![]() .
.
We also give the definition of the adapted random field under this frame.
Definition 8 A random field![]() , where
, where ![]() is called adapted to the filtration
is called adapted to the filtration![]() , being associated to the pair
, being associated to the pair ![]() if
if ![]() for any
for any![]() , where A is a directed subset of
, where A is a directed subset of ![]() by some binary relation
by some binary relation![]() , which is reflexive, transitive and every pair has an upper bound.
, which is reflexive, transitive and every pair has an upper bound.
Definition 9 A random field![]() , where
, where![]() , has the Martingale Property if it is adapted to a filtration
, has the Martingale Property if it is adapted to a filtration![]() , being associated to the pair
, being associated to the pair![]() , while
, while![]() .
.
Definition 10 A random field![]() , where
, where![]() , has the Strictly Positive Martingale Property
, has the Strictly Positive Martingale Property
if it is adapted to a filtration![]() , being associated to the pair
, being associated to the pair![]() , it has the Martingale Property, while the filtration
, it has the Martingale Property, while the filtration ![]() is consisted by strictly positive projections.
is consisted by strictly positive projections.
We give some examples for the previously mentioned notions.
Example 11 If ![]() is a sub-algebra of the
is a sub-algebra of the ![]() -algebra
-algebra ![]() of Ω, then since
of Ω, then since ![]() is a sublattice of
is a sublattice of![]() , then
, then ![]() is an incomplete market of financial positions in
is an incomplete market of financial positions in ![]()
![]() .
.
Example 12 The subspace of partially linear functions M in the space ![]() is a complete market in
is a complete market in![]() , due to the Stone-Weierstrass Theorem. We notice that the partially linear functions defined on
, due to the Stone-Weierstrass Theorem. We notice that the partially linear functions defined on ![]() is actually
is actually
the sublattice generated by the bi-set of functions![]() , where
, where![]() ,
,![]() . We
. We
notice that in this case, the span of this bi-set is a lattice-subspace of ![]() (see also [11] ).
(see also [11] ).
Example 13 A finite-dimensional sublattice ![]() of
of ![]() is an incomplete market in
is an incomplete market in![]() . As a lattice- subspace, it actually has a positive basis with nodes ([11] , Pr. 2.2), hence the equivalent positive projection
. As a lattice- subspace, it actually has a positive basis with nodes ([11] , Pr. 2.2), hence the equivalent positive projection ![]() is defined as follows:
is defined as follows:
![]()
where ![]() and
and ![]() are the nodes of the positive basis of
are the nodes of the positive basis of![]() .
.
Example 14 A sequence of sublattices ![]() of
of ![]() characterized by increasing non-terminal parts of the sequence
characterized by increasing non-terminal parts of the sequence
![]()
which has different terms in the sense ![]() is a filtration of
is a filtration of![]() , since
, since ![]() is the node for the one- dimensional subspace
is the node for the one- dimensional subspace![]() ,
, ![]() is the set of nodes of the positive basis of
is the set of nodes of the positive basis of ![]() and so on.
and so on.
Example 15 An increasing net of sub-![]() -algebras
-algebras ![]() of Ω, being a non-empty set, where A is a non- empty directed set, induces as it is well-known the existence of a filtration in
of Ω, being a non-empty set, where A is a non- empty directed set, induces as it is well-known the existence of a filtration in![]() , where
, where ![]() is supposed to be a probability space associated to the measurable space
is supposed to be a probability space associated to the measurable space![]() . The relevant net of sublattices is:
. The relevant net of sublattices is:
![]()
A may denote a set of cardinals, where if we start from a certain cardinal number![]() , then the cardinality of
, then the cardinality of ![]() -algebra
-algebra ![]() as a class of objects is at most equal to
as a class of objects is at most equal to ![]() and it is surely greater than
and it is surely greater than![]() .
.
Example 16 The filtration of the Example 14 is not strictly positive. This holds because if we pick a sublattice ![]() whose positive basis’ nodes is the set:
whose positive basis’ nodes is the set:
![]()
If![]() , this does not imply
, this does not imply ![]() if
if![]() . For example,
. For example, ![]() , but
, but![]() .
.
Example 17 If ![]() is a Banach lattice with order continuous norm and
is a Banach lattice with order continuous norm and ![]() is a projection band, namely
is a projection band, namely![]() , then
, then ![]() is norm-closed. The projection
is norm-closed. The projection ![]() is strictly positive since it is positive and
is strictly positive since it is positive and![]() , implies that since
, implies that since![]() , where
, where ![]() and
and![]() ,
,![]() .
. ![]() and
and![]() , hence
, hence ![]() and finally x = 0. The same situation is valid for Kantorovich-Banach spaces (or else KB-spaces), in which
and finally x = 0. The same situation is valid for Kantorovich-Banach spaces (or else KB-spaces), in which![]() . Such examples of spaces are reflexive Banach lattices like
. Such examples of spaces are reflexive Banach lattices like ![]() and
and ![]() -spaces.
-spaces.
Example 18 Let us consider a Banach lattice ![]() which has a Schauder basis:
which has a Schauder basis:
![]()
which is moreover a positive basis. Also, suppose that:
![]()
are finite-dimensional sublattices of![]() . Then,
. Then,
![]()
is a filtration, because ![]() and
and![]() , since
, since ![]() is a positive basis of
is a positive basis of ![]() itself. This is the case for
itself. This is the case for![]() .
.
3. Order Versions for the Fundamental Theorems of Asset Pricing
In the proof of the two next Theorems we use the following:
Lemma 19 A positive projection![]() , where
, where ![]() is a Banach lattice and
is a Banach lattice and ![]() is a positive sublattice of it, is a continuous operator.
is a positive sublattice of it, is a continuous operator.
Proof: Obvious, because every positive operator from a Banach lattice into to a locally solid Riesz space, is continuous.
Theorem 20 (Order 1st Fundamental Theorem of Asset Pricing) Let ![]() be a Banach lattice and
be a Banach lattice and ![]() be a sublattice of
be a sublattice of![]() . If
. If ![]() admits a strictly positive projection, then every strictly positive and continuous func- tional
admits a strictly positive projection, then every strictly positive and continuous func- tional![]() , admits a strictly positive, continuous extension on
, admits a strictly positive, continuous extension on![]() . Also, if
. Also, if ![]() is a Banach lattice and
is a Banach lattice and ![]() is a sublattice of
is a sublattice of ![]() such that every strictly positive and continuous functional
such that every strictly positive and continuous functional![]() , admits a strictly positive, continuous extension on
, admits a strictly positive, continuous extension on![]() , then
, then ![]() admits a strictly positive projection.
admits a strictly positive projection.
Proof: The adjoint operator of the strictly positive projection ![]() is an injection. Hence
is an injection. Hence ![]() is a continuous, strictly positive functional of
is a continuous, strictly positive functional of![]() . This is due to the duality:
. This is due to the duality:
![]()
For the proof of the opposite, we have the following: We define the projection ![]() as follows.
as follows.![]() .
. ![]() is a positive operator from a Banach lattice into a locally solid Riesz space. Hence it is continuous. By duality for some
is a positive operator from a Banach lattice into a locally solid Riesz space. Hence it is continuous. By duality for some ![]() strictly positive, continuous functional
strictly positive, continuous functional ![]() of
of![]() ,
,
![]()
Hence if we suppose that there is some ![]() such that
such that![]() , while
, while![]() . But this leads to a contradiction.
. But this leads to a contradiction.
Corollary 21 If ![]() is a Banach lattice which has the Strictly Positive Martingale Property with respect to some filtration
is a Banach lattice which has the Strictly Positive Martingale Property with respect to some filtration![]() , where
, where ![]() is a directed set. If
is a directed set. If ![]() such that
such that![]() , then every strictly positive and continuous functional
, then every strictly positive and continuous functional![]() , admits a strictly positive, continuous extension on
, admits a strictly positive, continuous extension on![]() .
.
Corollary 22 Let ![]() be a Banach lattice of financial positions and
be a Banach lattice of financial positions and ![]() be an incomplete market, such that
be an incomplete market, such that ![]() is a market model. If
is a market model. If ![]() admits a strictly positive projection, then for every price system
admits a strictly positive projection, then for every price system![]() , the market model
, the market model ![]() is viable.
is viable.
The existence of a strictly positive projection may be replaced by the Strictly Positive Martingale Property with respect to some filtration in the statement of the above Theorem. The term viable is the one established in the seminal work of D.M. Kreps (see [3] , p. 18-19).
Theorem 23 (Order 2nd Fundamental Theorem of Asset Pricing) Let ![]() be a Banach lattice and
be a Banach lattice and ![]() be a dense sublattice of
be a dense sublattice of![]() . If
. If ![]() admits a strictly positive projection, then every strictly positive and continuous functional
admits a strictly positive projection, then every strictly positive and continuous functional![]() , admits a unique strictly positive, continuous extension on
, admits a unique strictly positive, continuous extension on![]() . Also, let
. Also, let ![]() be a Banach lattice and
be a Banach lattice and ![]() be a sublattice of E such that M admits a strictly positive projection. Moreover, every strictly positive and continuous functional
be a sublattice of E such that M admits a strictly positive projection. Moreover, every strictly positive and continuous functional![]() , admits a unique strictly positive, continuous extension on
, admits a unique strictly positive, continuous extension on![]() . Then
. Then ![]() is dense in
is dense in![]() .
.
Proof: Since M is a dense sublattice of E, the adjoint (linear by the duality![]() )
)
operator ![]() of the strictly positive projection
of the strictly positive projection ![]() is a surjection. Hence for any
is a surjection. Hence for any![]() ,
,
there is some![]() , such that
, such that![]() , or else by duality relations:
, or else by duality relations:
![]()
For the converse, we have that for any![]() , there is some
, there is some![]() , such that
, such that![]() , or else by duality relations:
, or else by duality relations:
![]()
where ![]() is a strictly positive projection. This implies that
is a strictly positive projection. This implies that ![]() is a surjection, which is equivalent to the fact that
is a surjection, which is equivalent to the fact that ![]() is dense in
is dense in![]() .
.
Corollary 24 If ![]() is a Banach lattice which has the Strictly Positive Martingale Property with respect to some filtration
is a Banach lattice which has the Strictly Positive Martingale Property with respect to some filtration![]() , where A is a directed set. If
, where A is a directed set. If ![]() is an element of
is an element of ![]() such that
such that ![]() is a dense sublattice of
is a dense sublattice of![]() , then every strictly positive and continuous functional
, then every strictly positive and continuous functional![]() , admits a unique strictly positive, continuous extension on
, admits a unique strictly positive, continuous extension on![]() .
.
Corollary 25 Let ![]() be a Banach lattice of financial positions and
be a Banach lattice of financial positions and ![]() be a complete market, such that
be a complete market, such that ![]() is a market model. If
is a market model. If ![]() admits a strictly positive projection, then for every price system
admits a strictly positive projection, then for every price system![]() , the market model
, the market model ![]() is viable.
is viable.
The term viable is the one established in the seminal work of D.M. Kreps (see [3] , pp. 18-19).
We may notice that our Theorem does not make any reference to the No -Free Lunch Condition, but it simply extends the No-Arbitrage Property all over the space![]() . Theorem 23 is the analog of the usual 2nd FTAP, which implies that the (local) Equivalent Martingale Measures’ set of a complete market is a singleton, while under this class of market spaces the uniqueness of the (strictly positive) extension of a price system all over the space of financial positions is achieved under no presence of the No-Free Lunch Condition, too.
. Theorem 23 is the analog of the usual 2nd FTAP, which implies that the (local) Equivalent Martingale Measures’ set of a complete market is a singleton, while under this class of market spaces the uniqueness of the (strictly positive) extension of a price system all over the space of financial positions is achieved under no presence of the No-Free Lunch Condition, too.
Let us see some Examples which confirm the connection of the above Theorems to well-known models of Mathematical Finance.
Example 26 Let ![]() be a probability space endowed with an
be a probability space endowed with an ![]() -dimensional Brownian motion
-dimensional Brownian motion ![]()
![]() , where
, where![]() . Denote by
. Denote by ![]() the filtration that this Brownian motion
the filtration that this Brownian motion
generates, i.e.,![]() . We assume a financial market consisting of
. We assume a financial market consisting of ![]() assets whose prices
assets whose prices
are modelled by an ![]() -adapted,
-adapted, ![]() -dimensional Itô process
-dimensional Itô process ![]()
![]() of the form
of the form ![]() where:
where:
![]()
![]()
![]()
![]()
where ![]() is the
is the ![]() -th row
-th row ![]() of the
of the ![]() -matrix process
-matrix process![]() . The process
. The process ![]() repre- sents the price of a riskless asset (where
repre- sents the price of a riskless asset (where ![]() is the interest rate process which is supposed to have bounded values), while the
is the interest rate process which is supposed to have bounded values), while the ![]() -th component
-th component![]() , of the process
, of the process![]() , represents the evolution of the price of the
, represents the evolution of the price of the ![]() -th asset (stock). The price of the riskless asset may be used as numeraire. Suppose that
-th asset (stock). The price of the riskless asset may be used as numeraire. Suppose that![]() . If
. If ![]() is a stochastic exponential, then as it is well-known, the following relation holds:
is a stochastic exponential, then as it is well-known, the following relation holds:
![]()
where ![]() is the probability measure defined on
is the probability measure defined on ![]() as follows:
as follows:![]() , according to the
, according to the
Girsanov-Cameron-Martin Theorem. Taking mean values over ![]() we have:
we have:
![]()
which in terms of evaluation maps’ values is interpreted as follows:
![]()
The equivalent Riesz pairs are:
![]()
where the strictly positive projection ![]() is
is![]() , the strictly positive linear functional
, the strictly positive linear functional ![]() is
is ![]() and its strictly positive extension
and its strictly positive extension
![]() is
is![]() . This Example gives also a Hilbert space taste, due to the presence of
. This Example gives also a Hilbert space taste, due to the presence of ![]() -spaces, see also [12] .
-spaces, see also [12] .
Example 27
![]()
holds for the unique possible change of measure![]() , if the market is complete for example in the Black-Scholes model and this arises indeprendently from the unique solution of the market-price-of-risk equation.
, if the market is complete for example in the Black-Scholes model and this arises indeprendently from the unique solution of the market-price-of-risk equation.
Finally, we may revisit the Example constructed in [4] , in order to quote it.
Example 28 The actual form of the elements of the subspace M of ![]() is described by the following strictly positive projection:
is described by the following strictly positive projection:
![]()
![]() is a sublattice of
is a sublattice of ![]() under the usual component-wise ordering. Also,
under the usual component-wise ordering. Also, ![]() , while according to
, while according to
Theorem 3, a strictly positive extension of ![]() all over
all over ![]() exists, through duality relation
exists, through duality relation ![]()
![]() .
.
4. The Finite-State, One Period-Model Case
We will show how the above Theorems 3, 23 are applied in finite -state space models.
Let us consider the two-date market model in which the number of states of the world is denotes by![]() , while the time-periods are denoted by 0 and 1, respectively. We also consider an incomplete market of primitive assets whose time-period −1 payoffs are the positive, linearly independent vectors
, while the time-periods are denoted by 0 and 1, respectively. We also consider an incomplete market of primitive assets whose time-period −1 payoffs are the positive, linearly independent vectors ![]() of
of![]() , whose span is denoted by
, whose span is denoted by![]() . We suppose that
. We suppose that ![]() contains the riskless asset
contains the riskless asset![]() , while
, while![]() , which implies
, which implies
standard incompleteness. We also assume a time-period![]() , no-arbitrage price
, no-arbitrage price ![]() for the pri-
for the pri-
mitive assets. As it is well-known from ([7] , p. 4), ![]() is identified to the sublattice
is identified to the sublattice ![]() of
of ![]() generated by
generated by![]() . We also remind of the following Projection Basis Theorem for sublattices of
. We also remind of the following Projection Basis Theorem for sublattices of![]() , which arises from both ( [13] , Th. 3.7), ( [14] , Th. 9).
, which arises from both ( [13] , Th. 3.7), ( [14] , Th. 9).
Theorem 29 Let ![]() be a
be a ![]() -dimensional subspace of
-dimensional subspace of ![]() with
with ![]() generated by the positive elements
generated by the positive elements ![]() in which the riskless bond 1 is a marketed asset
in which the riskless bond 1 is a marketed asset![]() . Suppose that the range
. Suppose that the range ![]() of the basic function
of the basic function ![]() of the elements
of the elements ![]() is the finite set
is the finite set ![]() of the simplex
of the simplex ![]() of
of ![]() (note that
(note that![]() ). Suppose that the first
). Suppose that the first ![]() vectors of this set are linearly independent. If we suppose that the vectors
vectors of this set are linearly independent. If we suppose that the vectors ![]() are such that
are such that ![]() and
and ![]() where
where
![]() where
where ![]() and
and ![]() (which are
(which are
the vectors indicated by ( [13] , Th. 3.7), then,
1)![]() .
.
2) ![]()
3) If ![]() with
with ![]() and
and ![]() then the vectors
then the vectors ![]() defined by:
defined by:
![]()
where ![]() is the
is the ![]() matrix whose columns are the vectors
matrix whose columns are the vectors ![]() are a basis of
are a basis of ![]() called projection basis. This basis has the property: The
called projection basis. This basis has the property: The ![]() first coordinates of an element
first coordinates of an element ![]() in the positive basis of
in the positive basis of ![]() coincide with the coordinates of the expansion of
coincide with the coordinates of the expansion of ![]() in the basis
in the basis![]() .
.
Also, according to what is mentioned in [7] about the completion of an incomplete market ![]() by options and by following the notation we introduced,
by options and by following the notation we introduced, ![]() , where
, where ![]() and
and ![]() is a maximal set of linearly independent, positive vectors of
is a maximal set of linearly independent, positive vectors of![]() . Due to ([7] , Th. 21),
. Due to ([7] , Th. 21), ![]() are portfolios of call and put options written on elements of
are portfolios of call and put options written on elements of![]() , especially since
, especially since![]() .
.
The dimension equation which holds in the case of the no-arbitrage price![]() , is:
, is:
![]()
where ![]() denotes the subspace of
denotes the subspace of ![]() generated by the columns of the payoff matrix
generated by the columns of the payoff matrix ![]() of the primitive securities, while
of the primitive securities, while ![]() denotes the orthogonal subspace of it. Due to the characterization of the ab- sence of arbitrage in the primitive asset market (see [15] , Th. 9.2), there is at least one
denotes the orthogonal subspace of it. Due to the characterization of the ab- sence of arbitrage in the primitive asset market (see [15] , Th. 9.2), there is at least one ![]() such that
such that ![]() where
where![]() . This implies that
. This implies that ![]() in this case, while
in this case, while ![]() if by
if by ![]() we also denote the
we also denote the ![]() matrix whose columns are the vectors
matrix whose columns are the vectors![]() . The last relation arises from
. The last relation arises from
![]() if we suppose that
if we suppose that![]() . Then
. Then ![]() and if we denote
and if we denote![]() , we obtain
, we obtain
the last relation. As it is implied in [7] ![]() is determined by the positive basis
is determined by the positive basis ![]() of it.
of it.
We also have the following:
Theorem 30 Any ![]() such that
such that ![]() implies a no-arbitrage price
implies a no-arbitrage price ![]() for which the price
for which the price
![]() of the portfolio
of the portfolio ![]() or else the price of the asset
or else the price of the asset ![]() lying in the completion
lying in the completion
![]() to be equal to the price of the same asset under
to be equal to the price of the same asset under ![]() if
if![]() , where
, where ![]() are the vectors indicated by the Projection Basis Theorem.
are the vectors indicated by the Projection Basis Theorem.
Proof: Consider the vector![]() . The above vector satisfies the following equalities:
. The above vector satisfies the following equalities:
![]()
The definition of the vector ![]() allows us to prove that it is a no-arbitrage price in the subspace generated by the vectors
allows us to prove that it is a no-arbitrage price in the subspace generated by the vectors ![]() which is the completion by options
which is the completion by options ![]() of
of![]() . If for a portfolio
. If for a portfolio ![]() the payoff
the payoff ![]() lies in the positive cone
lies in the positive cone ![]() except
except![]() , then:
, then:
![]() ,
,
because![]() . Also, from the Projection Basis Theorem 29, if
. Also, from the Projection Basis Theorem 29, if![]() , this means that:
, this means that:
![]() .
.
Hence ![]() in this case, which is equal to the valuation of the portfolio
in this case, which is equal to the valuation of the portfolio ![]()
of the primitive assets under![]() . We remind that
. We remind that ![]() is the space of the financial positions, since
is the space of the financial positions, since ![]() is actually equal to this space according to ([7] , Pr. 6).
is actually equal to this space according to ([7] , Pr. 6).
Theorem 31 (First Order Finite Fundamental Theorem of Asset Pricing) For any subspace ![]() of
of![]() , where
, where ![]() and
and ![]() and
and ![]()
![]() are linearly inde- pendent, every strictly positive linear functional of
are linearly inde- pendent, every strictly positive linear functional of ![]() has a strictly positive extension on
has a strictly positive extension on![]() .
.
Proof: Every strictly positive functional ![]() defines a no -arbitrage price
defines a no -arbitrage price ![]() on
on ![]() as follows:
as follows:![]() . According to Theorem 30,
. According to Theorem 30, ![]() for some
for some ![]() such that
such that ![]() is a strictly positive extension of f on
is a strictly positive extension of f on![]() , where
, where![]() , where
, where ![]() is the support of the vector
is the support of the vector ![]() of the positive basis of
of the positive basis of![]() , see ([7] , Th. 6).
, see ([7] , Th. 6).
Proposition 32 If we suppose that the vectors of the date-1 payoffs of the primitive assets ![]() are linearly independent and
are linearly independent and![]() , then
, then![]() , where
, where![]() , except a set of vectors
, except a set of vectors ![]() of Lebesgue measure zero in
of Lebesgue measure zero in![]() .
.
Proof: In the last part of [7] , a brief proof was given about the fact that resolving markets have the property![]() . It is also well-known that resolving matrices are in general position, namely the complement of the set of them is a null-set in the vector space of the matrices
. It is also well-known that resolving matrices are in general position, namely the complement of the set of them is a null-set in the vector space of the matrices![]() , whose entries are real numbers. Hence the super-set of all the
, whose entries are real numbers. Hence the super-set of all the ![]() -matrices (markets), such that
-matrices (markets), such that ![]() where
where ![]() are linearly independent and they have the property that
are linearly independent and they have the property that ![]() are also in general position.
are also in general position.
Theorem 33 (Second Order Finite Fundamental Theorem of Asset Pricing) For almost any subspace ![]() of
of![]() , where
, where ![]() and
and ![]() and
and ![]()
![]() are linearly inde- pendent, every strictly positive linear functional of
are linearly inde- pendent, every strictly positive linear functional of ![]() has a unique strictly positive extension on
has a unique strictly positive extension on![]() .
.
Proof: Every strictly positive functional ![]() defines a no-arbitrage price
defines a no-arbitrage price ![]() on
on ![]() as follows:
as follows:![]() . According to Theorem 30,
. According to Theorem 30, ![]() for a unique
for a unique![]() .
.
5. The Finite Multi-Period Model Case
Let us see what happens in the multi-period framework. We consider the event -tree model as it is presented in [15] , according to which there is a finite time -horizon![]() , a family of partitions F of
, a family of partitions F of ![]() such that
such that ![]() and
and ![]() is thinner than
is thinner than ![]() for any
for any ![]() in the sense
in the sense
that for any![]() , there is a
, there is a ![]() such that
such that![]() . Then the set
. Then the set ![]() is
is
the event-tree corresponding to the family of partitions![]() . Every event-tree
. Every event-tree ![]() is a model of information re- vealing along the time-periods of
is a model of information re- vealing along the time-periods of![]() . We also consider
. We also consider ![]() assets (financial contracts) whose payoff vectors are
assets (financial contracts) whose payoff vectors are ![]() and if we denote by
and if we denote by ![]() the physical number which is equal to the cardinality of the nodes of the event-tree
the physical number which is equal to the cardinality of the nodes of the event-tree![]() , these are actually vectors of
, these are actually vectors of![]() . We also suppose that the price vectors of the assets are
. We also suppose that the price vectors of the assets are![]() , where
, where ![]() if
if ![]() and the set
and the set ![]() denotes the set of nodes of the event-tree corresponding to the time-period
denotes the set of nodes of the event-tree corresponding to the time-period![]() . If we suppose that these price vectors do not provide arbitrage opportunities in the market of the assets
. If we suppose that these price vectors do not provide arbitrage opportunities in the market of the assets![]() , then since the market is incomplete there is at least one node-price vector
, then since the market is incomplete there is at least one node-price vector ![]() such that
such that![]() , where
, where ![]() is the payoff matrix of this market as it is indicated in ([15] , Ch. 4). In order to simplify things, we may suppose that
is the payoff matrix of this market as it is indicated in ([15] , Ch. 4). In order to simplify things, we may suppose that![]() , where
, where![]() . We also suppose that one of the assets of the market is riskless, or else that for any
. We also suppose that one of the assets of the market is riskless, or else that for any ![]() which corresponds to the same time-period, its payoff is the same. Also, this asset’s initial price
which corresponds to the same time-period, its payoff is the same. Also, this asset’s initial price ![]() is equal to 1. The submatrix
is equal to 1. The submatrix ![]() for any
for any ![]() is the
is the ![]() -matrix whose rows are the vectors
-matrix whose rows are the vectors ![]() of
of![]() , indicating the payoffs and the ex-payoff price of the J primitive securities at the node
, indicating the payoffs and the ex-payoff price of the J primitive securities at the node![]() . The cardinality of
. The cardinality of ![]() is denoted by
is denoted by![]() .
.
The market of the securities is complete or as it is usually said the securities’ markets are dynamically complete, if every contingent claim ![]() can be replicated by a portfolio
can be replicated by a portfolio ![]()
![]() . In order to understand the next, we remind of the following,
. In order to understand the next, we remind of the following,
Definition 34 The forward -start call option written on a contingent claim ![]() with exercise- price
with exercise- price ![]() at the node
at the node ![]() given that
given that![]() , is equal to:
, is equal to:
![]()
Definition 35 The forward -start put option written on a contingent claim ![]() with exercise- price
with exercise- price ![]() at the node
at the node ![]() given that
given that![]() , is equal to:
, is equal to:
![]()
As a reference for these options we append to ([16] , Par. 9.2).
The market is (dynamically) complete if and only if it is one-period complete for any non-terminal node![]() , namely if
, namely if![]() . Otherwise it is called incomplete. For any
. Otherwise it is called incomplete. For any ![]() such that
such that![]() , and moreover there is a non-terminal node
, and moreover there is a non-terminal node ![]() such that for the corresponding sub-
such that for the corresponding sub-
matrix ![]() of
of![]() ,
, ![]() holds, we may add forward-start op-
holds, we may add forward-start op-
tions of the form![]() , where
, where ![]() to make it complete. In the
to make it complete. In the
same way we may talk about the completion by options of the span ![]() with re-
with re-
spect to the asset ![]() which may be denoted by
which may be denoted by ![]() for any
for any![]() .
. ![]() is the vector of the
is the vector of the
Euclidean space ![]() such that
such that![]() . In a way similar to [7] , the dimension of the
. In a way similar to [7] , the dimension of the
completion ![]() is denoted by
is denoted by![]() . It is obvious that we may reach a complete market if and only
. It is obvious that we may reach a complete market if and only
if ![]() for any
for any![]() . A question which also arises in this case is how the new assets introduced in
. A question which also arises in this case is how the new assets introduced in
a submarket ![]() with
with ![]() in order to reach
in order to reach ![]() are priced. The answer is given in the next Theorem, being equivalent to Theorem 29.
are priced. The answer is given in the next Theorem, being equivalent to Theorem 29.
Theorem 36 For any submarket ![]() with
with ![]() and any
and any ![]()
where![]() , where
, where ![]() is a no-arbitrage price vector for the assets
is a no-arbitrage price vector for the assets![]() .
.
![]() is a price vector which assigns the price
is a price vector which assigns the price ![]() to the portfolio
to the portfolio![]() . Specifi-
. Specifi-
cally, the price of the asset ![]() lying in the completion
lying in the completion ![]() is equal to the price of the
is equal to the price of the
same asset under ![]() if
if![]() , where
, where ![]() are the vectors indicated by the Projection Basis Theorem.
are the vectors indicated by the Projection Basis Theorem.
Proof: Consider the vector![]() , where
, where![]() . The above vector satisfies the following equalities:
. The above vector satisfies the following equalities:
![]()
The definition of the vector ![]() allows us to prove that it is a no-arbitrage price in the subspace generated by the vectors
allows us to prove that it is a no-arbitrage price in the subspace generated by the vectors ![]() which is the completion by options
which is the completion by options![]() ,
,
![]() .
.
If for a portfolio ![]() the payoff
the payoff ![]() lies in the positive cone
lies in the positive cone ![]() except
except![]() , then:
, then:
![]() ,
,
because![]() . Also, from the Projection Basis Theorem, if
. Also, from the Projection Basis Theorem, if![]() , this means that
, this means that
![]() . Hence
. Hence ![]() in this case, which is equal to the valuation of the
in this case, which is equal to the valuation of the
portfolio ![]() of the primitive assets under
of the primitive assets under![]() . This concludes the proof.
. This concludes the proof.
Theorem 37 (First Order Event-Tree Fundamental Theorem of Asset Pricing). For any submarket
![]() with
with ![]() and any
and any ![]() with
with![]() , every strictly
, every strictly
positive linear functional of ![]() has a strictly positive extension on
has a strictly positive extension on![]() .
.
Proof: If ![]() is a strictly positive functional of
is a strictly positive functional of![]() , then this implies a no-arbi- trage price
, then this implies a no-arbi- trage price ![]() and since
and since ![]() is given,
is given,![]() . The extension of
. The extension of ![]() is
is ![]() for
for
some ![]() such that
such that ![]() is a strictly positive extension of f on
is a strictly positive extension of f on![]() , where
, where
![]() , where
, where ![]() is the support of the vector
is the support of the vector ![]() of the po-
of the po-
sitive basis of![]() , see ([7] , Th. 6).
, see ([7] , Th. 6).
Theorem 38 (Second Order Finite Fundamental Theorem of Asset Pricing) If the market is complete, then for any submarket![]() , every strictly positive linear functional of
, every strictly positive linear functional of ![]() has a unique strictly
has a unique strictly
positive extension on![]() .
.
Proof: Since the market is complete, ![]() and there is a unique
and there is a unique ![]() with
with
![]() , If
, If ![]() is a strictly positive functional of
is a strictly positive functional of![]() , then this implies
, then this implies
a no-arbitrage price ![]() and since
and since ![]() is given,
is given,![]() . The unique extension of
. The unique extension of ![]() is
is
![]() for some
for some ![]() such that
such that ![]() is a strictly positive extension of
is a strictly positive extension of ![]()
on![]() , where
, where![]() , where
, where ![]() is the support of the vec-
is the support of the vec-
tor ![]() of the positive basis of
of the positive basis of![]() , see ([7] , Th. 6), since
, see ([7] , Th. 6), since ![]() is unique.
is unique.
6. General Cones Revisited
Let us consider a Banach space ![]() of financial positions, partially ordered by a closed cone
of financial positions, partially ordered by a closed cone![]() , which is not a lattice cone. Such a cone is for example a Bishop-Phepls cone, see ([17] , pp. 126-127), which is well-based and it has also interior points, hence it is not a lattice cone, according to ([17] , Th. 4.4.4). Of course, the set of strictly positive functionals of such a cone has not to be empty. This is the reason due to which the Lindelöf Property mentioned in [9] about the weak topology
, which is not a lattice cone. Such a cone is for example a Bishop-Phepls cone, see ([17] , pp. 126-127), which is well-based and it has also interior points, hence it is not a lattice cone, according to ([17] , Th. 4.4.4). Of course, the set of strictly positive functionals of such a cone has not to be empty. This is the reason due to which the Lindelöf Property mentioned in [9] about the weak topology ![]() defined on a dual system
defined on a dual system ![]() is important. Of course, there are cones which do not admit continuous strictly positive functionals. Such a cone is the positive cone of an
is important. Of course, there are cones which do not admit continuous strictly positive functionals. Such a cone is the positive cone of an ![]() space, where
space, where ![]() is uncountable.
is uncountable.
Also, in this section, the definition of (in)completeness are altered.
Definition 39 If M is a infinite-dimensional subspace of E ordered by the cone C, a market is an infinite- dimensional subspace of![]() , such that
, such that![]() .
.
Definition 40 A market is incomplete if![]() , while it is complete if
, while it is complete if![]() .
.
Then, the following versions of the Second and the First Fundamental Theorem of Asset Pricing are deduced, respectively.
Theorem 41 Let ![]() be a Banach space with an unconditional basis. Then a non-lattice one exists, which makes
be a Banach space with an unconditional basis. Then a non-lattice one exists, which makes ![]() a complete market and every strictly positive functional of this cone admits a unique strictly positive extension.
a complete market and every strictly positive functional of this cone admits a unique strictly positive extension.
Proof: As it is well-known from ([18] , Th. 4.2.22), the cone of the unconditional basis ![]()
![]() makes X a Banach lattice under an equivalent norm. According to ([8] , Th.
makes X a Banach lattice under an equivalent norm. According to ([8] , Th.
5.7) there is a strongly reflexive cone (see [8] , Def. 5.1) C in E+, such that![]() . Also, since the one-dimensional-subspace projections
. Also, since the one-dimensional-subspace projections ![]() are continuous, according to ([18] , Cor. 4.2.26), the operator
are continuous, according to ([18] , Cor. 4.2.26), the operator
![]() is a continuous projection from E ordered by
is a continuous projection from E ordered by ![]() (which is also the cone of the positive basis)
(which is also the cone of the positive basis)
to ![]() being ordered by
being ordered by![]() . Also, we notice that
. Also, we notice that ![]() is strictly positive in the sense that
is strictly positive in the sense that![]() , whenever
, whenever![]() . Hence,
. Hence, ![]() may be taken as a strictly positive projection, and consequently we may repeat the proof of Theorem 23.
may be taken as a strictly positive projection, and consequently we may repeat the proof of Theorem 23.
Theorem 42 Let E be a Banach space with an unconditional basic sequence. Then, for the incomplete market ![]() arising from the basic sequence, there exists a non-lattice cone
arising from the basic sequence, there exists a non-lattice cone![]() , such that
, such that ![]() and strictly posi- tive functional of this cone admits a strictly positive extension on
and strictly posi- tive functional of this cone admits a strictly positive extension on![]() .
.
Proof: According to ([8] , Cor. 5.8) there is a strongly reflexive cone (see [8] , Def. 5.1) ![]() in
in![]() , such that
, such that![]() , while for any uncoditional basic sequence it is well-known that (see [18] , Th. 4.2.22) its cone
, while for any uncoditional basic sequence it is well-known that (see [18] , Th. 4.2.22) its cone ![]() makes
makes ![]() a Banach lattice (under an equivalent norm). Also, since the one-dimensional-subspace projec-
a Banach lattice (under an equivalent norm). Also, since the one-dimensional-subspace projec-
tions ![]() are continuous, according to ([18] , Cor. 4.2.26) the operator
are continuous, according to ([18] , Cor. 4.2.26) the operator ![]() is a continuous
is a continuous
projection from ![]() ordered by
ordered by ![]() (which is also the cone of the positive basis) to
(which is also the cone of the positive basis) to ![]() being ordered by
being ordered by![]() . Also, we notice that P is strictly positive in the sense that
. Also, we notice that P is strictly positive in the sense that![]() , whenever
, whenever![]() . Hence,
. Hence, ![]() may be taken as a strictly positive projection, and consequently we may repeat the proof of Theorem 3.
may be taken as a strictly positive projection, and consequently we may repeat the proof of Theorem 3.
In the proof of ([8] , Th. 5.7) the strongly reflexive cone’s construction relies exactly on the existence of an unconditional basis for the Banach space E. Then we may understand that the crucial point for the above Theorems is the existence of a basic sequence for the Banach space E. We may remind the seminal work by Bessaga-Pelczynski [19] essentials on this topic.
Cite this paper
Christos E.Kountzakis, (2014) On the Order Form of the Fundamental Theorems of Asset Pricing. Journal of Mathematical Finance,04,221-233. doi: 10.4236/jmf.2014.44019
References
- 1. Delbaen, F. and Schachermayer, W. (1994) A General Version of the Fundamental Theorem of Asset Pricing. Mathematische Annalen, 300, 463-520.
http://dx.doi.org/10.1007/BF01450498
- 2. Delbaen, F. and Schachermayer, W. (1998) The Fundamental Theorem of Asset Pricing for Unbounded Stochastic Processes. Mathematische Annalen, 312, 215-250.
http://dx.doi.org/10.1007/s002080050220
- 3. Kreps, D.M. (1981) Arbitrage and Equilirium in Economies with Infinitely Many Commodities. Journal of Mathematical Economics, 8, 15-35.
http://dx.doi.org/10.1016/0304-4068(81)90010-0
- 4. Schachermayer, W. (2002) No Arbitrage: On the Work of David Kreps. Positivity, 6, 359-368.
http://dx.doi.org/10.1023/A:1020262419556
- 5. Acciaio, B., Beiglbock, M., Penkner, F. and Schachermayer, W. (2013) A Model-Free Version of the Fundamental Theorem of Asset Pricing and the Super-Replication Theorem. Mathematical Finance (to Appear), 6 December 2013.
http://dx.doi.org/10.1111/mafi.12060
- 6. Troitsky, V.G. (2005) Martingales in Banach lattices. Positivity, 9, 437-456.
http://dx.doi.org/10.1007/s11117-004-2769-1
- 7. Kountzakis, C. and Polyrakis, I.A. (2006) The Completion of Security Markets. Decisions in Economics and Finance, 29, 1-21.
http://dx.doi.org/10.1007/s10203-006-0059-z
- 8. Casini, E., Miglierina, E., Polyrakis, I.A. and Xanthos, F. (2013) Reflexive Cones. Positivity, 17, 911-933.
http://dx.doi.org/10.1007/s11117-012-0212-6
- 9. Rokhlin, D.B. (2005) The Kreps-Yan Theorem for . International Journal of Mathematics and Mathematical Sciences, 17, 2749-2756.
- 10. Rokhlin, D.B. (2009) The Kreps-Yan Theorem for Ideal Banach Spaces. Siberian Mathematical Journal, 50, 162-166.
- 11. Polyrakis, I.A. (1996) Finite-Dimensional Lattice-Subspaces of and Curves of . Transactions of the American Mathematical Society, 348, 2793-2810.
http://dx.doi.org/10.1090/S0002-9947-96-01639-X
- 12. Schachermayer, W. (1992) A Hilbert Space Proof of the Fundamental Theorem of Asset Pricing in Finite Discrete Time. Insurance: Mathematics and Economics, 11, 249-257.
http://dx.doi.org/10.1016/0167-6687(92)90013-2
- 13. Polyrakis, I.A. (1999) Minimal Lattice Subspaces. Transactions of the American Mathematical Society, 351, 4183-4203.
- 14. Polyrakis, I.A. (2003) Linear Optimization in and Portfolio Insurance. Optimization, 52, 221-239.
- 15. Magill, M. and Quinzii, M. (1996) Theory of Incomplete Markets. MIT Press, location.
- 16. Musiela, M. and Rutkowski, M. (1997) Martingale Methods in Financial Modelling. Applications of Mathematics, Mathematical Modelling and Applied Probability, Springer, Berlin.
http://dx.doi.org/10.1007/978-3-662-22132-7
- 17. Jameson, G. (1970) Ordered Linear Spaces. Lecture Notes in Mathematics, Springer-Verlag, Berlin.
- 18. Megginson, R.E. (1998) An Introduction to Banach Spaces. Springer, New York.
http://dx.doi.org/10.1007/978-1-4612-0603-3
- 19. Bessaga, C. and Pelczyński, A. (1958) On Bases and Unconditional convergence of Series in Banach Spaces. Studia Mathematica, 17, 151-164.
- 20. Aliprantis, C.D. and Border, K.C. (2005) Infinite Dimensional Analysis, A Hitchhiker’s Guide. 3rd Edition, Springer, Berlin.
Appendix
In this Section, we give some essential notions and results from the theory of partially ordered linear spaces which are used in this paper. For these notions and definitions, see ([17] , Ch. 1, Ch. 2, Ch. 3). Let ![]() be a (normed) linear space. A set
be a (normed) linear space. A set ![]() satisfying
satisfying ![]() and
and ![]() for any
for any ![]() is called wedge. A wedge for which
is called wedge. A wedge for which ![]() is called cone. A pair
is called cone. A pair ![]() where
where ![]() is a linear space and
is a linear space and ![]() is a binary relation on
is a binary relation on ![]() satisfying the following properties:
satisfying the following properties:
1) ![]() for any
for any ![]() (reflexive);
(reflexive);
2) If ![]() and
and ![]() then
then![]() , where
, where ![]() (transitive);
(transitive);
3) If ![]() then
then ![]() for any
for any ![]() and
and ![]() for any
for any![]() , where
, where ![]() (compatible with the linear structure of
(compatible with the linear structure of![]() ), is called partially ordered linear space. The binary relation
), is called partially ordered linear space. The binary relation ![]() in this case is a partial ordering on
in this case is a partial ordering on![]() . The set
. The set ![]() is called (positive) wedge of the partial ordering
is called (positive) wedge of the partial ordering ![]() of
of![]() . Given a wedge
. Given a wedge ![]() in
in![]() , the binary relation
, the binary relation ![]() defined as follows:
defined as follows:
![]()
is a partial ordering on![]() , called partial ordering induced by
, called partial ordering induced by ![]() on
on![]() . If the partial ordering
. If the partial ordering ![]() of the space
of the space ![]() is antisymmetric, namely if
is antisymmetric, namely if ![]() and
and ![]() implies
implies![]() , where
, where![]() , then
, then ![]() is a cone.
is a cone.
![]() denotes the linear space of all linear functionals of
denotes the linear space of all linear functionals of![]() , called algebraic dual while
, called algebraic dual while ![]() is the norm dual of
is the norm dual of![]() , in case where
, in case where ![]() is a normed linear space.
is a normed linear space.
Suppose that ![]() is a wedge of
is a wedge of![]() . A functional
. A functional ![]() is called positive functional of
is called positive functional of ![]() if
if ![]() for any
for any![]() .
. ![]() is a strictly positive functional of
is a strictly positive functional of ![]() if
if ![]() for any
for any![]() . A linear functional
. A linear functional ![]() where
where ![]() is a normed linear space, is called uniformly monotonic functional of
is a normed linear space, is called uniformly monotonic functional of ![]() if there is some real number
if there is some real number ![]() such that
such that ![]() for any
for any![]() . In case where a uniformly monotonic func-
. In case where a uniformly monotonic func-
tional of C exists, C is a cone. ![]() is the dual wedge of
is the dual wedge of ![]() in
in![]() . Also,
. Also,
by ![]() we denote the subset
we denote the subset ![]() of
of![]() . It can be easily proved that if C is a closed wedge of a reflexive space, then
. It can be easily proved that if C is a closed wedge of a reflexive space, then![]() . If
. If ![]() is a wedge of
is a wedge of![]() , then the set
, then the set ![]() is the dual wedge of
is the dual wedge of ![]() in
in![]() , where
, where ![]() denotes the natural embedding map from
denotes the natural embedding map from ![]() to the second dual space
to the second dual space ![]() of
of![]() . Note that if for two wedges
. Note that if for two wedges ![]() of
of![]() ,
, ![]() holds, then
holds, then![]() .
.
If C is a cone, then a set ![]() is called base of C if for any
is called base of C if for any ![]() there exists a unique
there exists a unique ![]() such that
such that![]() . The set
. The set ![]() where
where ![]() is a strictly positive functional of C is the base of
is a strictly positive functional of C is the base of ![]() defined by
defined by![]() .
. ![]() is bounded if and only if
is bounded if and only if ![]() is uniformly monotonic. If
is uniformly monotonic. If ![]() is a bounded base of
is a bounded base of ![]() such that
such that ![]() then
then ![]() is called well-based. If
is called well-based. If ![]() is well-based, then a bounded base of C defined by a
is well-based, then a bounded base of C defined by a ![]() exists. If
exists. If ![]() then the wedge
then the wedge ![]() is called generating, while if
is called generating, while if ![]() it is called almost generating. If C is generating, then
it is called almost generating. If C is generating, then ![]() is a cone of E* in case where E is a normed linear space. Also,
is a cone of E* in case where E is a normed linear space. Also, ![]() is a uniformly monotonic functional of C if and only if
is a uniformly monotonic functional of C if and only if![]() , where
, where ![]() denotes the norm-interior of
denotes the norm-interior of
![]() . If
. If ![]() is partially ordered by C, then any set of the form
is partially ordered by C, then any set of the form ![]() where
where ![]()
is called order-interval of E. If E is partially ordered by ![]() and for some
and for some![]() ,
, ![]() holds, then
holds, then ![]() is called order-unit of E. If E is a normed linear space, then if every interior point of C is an order-unit of E. If E is moreover a Banach space and
is called order-unit of E. If E is a normed linear space, then if every interior point of C is an order-unit of E. If E is moreover a Banach space and ![]() is closed, then every order-unit of E is an interior point of C. The partially ordered vector space E is a vector lattice if for any
is closed, then every order-unit of E is an interior point of C. The partially ordered vector space E is a vector lattice if for any![]() , the supremum and the infimum of
, the supremum and the infimum of ![]() with respect to the partial ordering defined by P exist in E. In this case
with respect to the partial ordering defined by P exist in E. In this case ![]() and
and ![]() are denoted by
are denoted by![]() ,
, ![]() respectively. If so,
respectively. If so, ![]() is the absolute value of
is the absolute value of ![]() and if E is also a normed space such that
and if E is also a normed space such that ![]() for any
for any![]() , then E is called normed lattice. If a normed lattice is a Banach space, then it is called Banach lattice. A Banach lattice E whose norm has the property
, then E is called normed lattice. If a normed lattice is a Banach space, then it is called Banach lattice. A Banach lattice E whose norm has the property ![]() is called AL-space. A set S in a vector lattice E is called solid if
is called AL-space. A set S in a vector lattice E is called solid if ![]() and
and ![]() implies
implies![]() . A solid vector subspace of a vector lattice is called ideal. An ideal
. A solid vector subspace of a vector lattice is called ideal. An ideal ![]() is a sublattice of E, i.e., a subspace of E such that
is a sublattice of E, i.e., a subspace of E such that ![]() if
if ![]() respectively. A net
respectively. A net ![]() in a vector lattice E is order convergent to
in a vector lattice E is order convergent to ![]() if
if
there is a net ![]() in E with
in E with![]() , such that
, such that ![]() for each
for each![]() . This convergence is denoted
. This convergence is denoted
by![]() . A set
. A set ![]() in E is order closed if
in E is order closed if ![]() and
and![]() , implies
, implies![]() . If
. If ![]() is also an ideal, then
is also an ideal, then ![]() is called band. A Banach lattice has order continuous norm, if for any net
is called band. A Banach lattice has order continuous norm, if for any net ![]() with
with![]() ,
, ![]() holds. A Banach lattice E which is a band in its second dual (in the sense of norm topology) is called Kantorovich-Banach space. If S is a subset of a vector lattice E, then its disjoint complement is the set
holds. A Banach lattice E which is a band in its second dual (in the sense of norm topology) is called Kantorovich-Banach space. If S is a subset of a vector lattice E, then its disjoint complement is the set![]() . If for a vector lattice E a band B satisfies the property
. If for a vector lattice E a band B satisfies the property![]() , then B is called projection band. Finally, if E is a partially ordered Banach space whose positive cone is
, then B is called projection band. Finally, if E is a partially ordered Banach space whose positive cone is![]() , if E has a
, if E has a
Schauder basis![]() , this basis is called positive basis if and only if
, this basis is called positive basis if and only if![]() . For
. For
linear lattices and positive bases see in ( [20] , Ch. 8), and [11] , respectively.




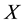 is equivalent to the existence of an equivalent martingale measure for
is equivalent to the existence of an equivalent martingale measure for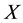 . It was shown in [1] that for a locally bounded
. It was shown in [1] that for a locally bounded 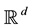 -valued semi-martingale
-valued semi-martingale 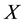 the condition of No Free Lunch with Vanishing Risk is equivalent to the existence of an equivalent local martingale measure for the process
the condition of No Free Lunch with Vanishing Risk is equivalent to the existence of an equivalent local martingale measure for the process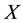 . It was proved in [2] that the local boundedness assumption on
. It was proved in [2] that the local boundedness assumption on  may be dropped under the notion of equivalent
may be dropped under the notion of equivalent 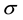 -martingale measure. The work [3] , also discussed in [4] , is still essential in this topic and actually this work’s results rely on what Kreps established as the viable market model consisted by an incomplete market and a linear price system on it. In the present work we are going to resolve the so-called Strictly Positive Extension Property from the financial aspect. The presence of heavy-tails in continuous time models and the possible change of frame from
-martingale measure. The work [3] , also discussed in [4] , is still essential in this topic and actually this work’s results rely on what Kreps established as the viable market model consisted by an incomplete market and a linear price system on it. In the present work we are going to resolve the so-called Strictly Positive Extension Property from the financial aspect. The presence of heavy-tails in continuous time models and the possible change of frame from 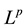 spaces to Orlicz spaces in order to fit the modelling requirements, oblige us to search for more general versions of the two FTAPs, mostly relied on the geometry of these spaces. Recently, in [5] , a Fundamental Theorem of Asset Pricing and a Super-Replication Theorem in a model-independent framework are both proposed. But these theorems are proved in the setting of finite, discrete time and a market consisting of a risky asset
spaces to Orlicz spaces in order to fit the modelling requirements, oblige us to search for more general versions of the two FTAPs, mostly relied on the geometry of these spaces. Recently, in [5] , a Fundamental Theorem of Asset Pricing and a Super-Replication Theorem in a model-independent framework are both proposed. But these theorems are proved in the setting of finite, discrete time and a market consisting of a risky asset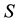 , as well as options written on this risky asset, too. Notions like the one of the strictly positive projection or that of the filtration are alike the ones met in [6] . A difference between our notion of strictly positive projection and the equivalent notion in [6] is that ours is weaker. That’s because if
, as well as options written on this risky asset, too. Notions like the one of the strictly positive projection or that of the filtration are alike the ones met in [6] . A difference between our notion of strictly positive projection and the equivalent notion in [6] is that ours is weaker. That’s because if 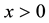 implies
implies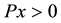 , this implies
, this implies , because if
, because if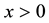 , it would be
, it would be . An important difference between the article of Troitsky and ours is that we extend the framework of Definitions so as to include cases of non-discrete time spaces. Another one is that we apply these notions in order to provide a new version of the two FTAP, while in [6] an important ordered -space theory of martingales in Banach lattices is developed. Finally, markets subspaces are taken to be sublattices because of the fact that we may include layers of call and put options written on an initial market space, as we remarked in [7] . The present paper is organized as follows: First, we provide some useful notions and definitions and examples for them, as well. Next, we prove the Order Form of the FTAP in the Banach-lattice case and in the next sections we provide the analog of these results in the finite-models case. We also explain the application of our results on the Black-Scholes-Merton model. We also compare them to the Example developed in [4] . The case of non-lattice cones is examined in the last section of the paper, in relation with the classes of reflexive and strongly reflexive cones, mentioned in [8] . The role of the existence of an unconditional basic sequence in a Banach space is also quoted in this section independently from the results provided in [8] , as an important condition for the extraction of results concerning FTAP. This condition is not irrelevant to ( [9] , Th. 1.1), about Lindelöf Properties of weak topology, but here it mainly concerns the construction of a Strictly Positive Projection Operator. On the other side, in the paper [10] ideals of
. An important difference between the article of Troitsky and ours is that we extend the framework of Definitions so as to include cases of non-discrete time spaces. Another one is that we apply these notions in order to provide a new version of the two FTAP, while in [6] an important ordered -space theory of martingales in Banach lattices is developed. Finally, markets subspaces are taken to be sublattices because of the fact that we may include layers of call and put options written on an initial market space, as we remarked in [7] . The present paper is organized as follows: First, we provide some useful notions and definitions and examples for them, as well. Next, we prove the Order Form of the FTAP in the Banach-lattice case and in the next sections we provide the analog of these results in the finite-models case. We also explain the application of our results on the Black-Scholes-Merton model. We also compare them to the Example developed in [4] . The case of non-lattice cones is examined in the last section of the paper, in relation with the classes of reflexive and strongly reflexive cones, mentioned in [8] . The role of the existence of an unconditional basic sequence in a Banach space is also quoted in this section independently from the results provided in [8] , as an important condition for the extraction of results concerning FTAP. This condition is not irrelevant to ( [9] , Th. 1.1), about Lindelöf Properties of weak topology, but here it mainly concerns the construction of a Strictly Positive Projection Operator. On the other side, in the paper [10] ideals of 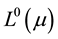 are used in order to deduce an FTAP-like result ( [10] , Lem. 1), while our results refer to sublattices.
are used in order to deduce an FTAP-like result ( [10] , Lem. 1), while our results refer to sublattices.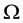 which is supposed to be an infinite set. The true state
which is supposed to be an infinite set. The true state 












































































































































































































































































































































































































































































































































































































































































































































































































