Journal of Mathematical Finance
Vol.04 No.02(2014), Article ID:42882,20 pages
10.4236/jmf.2014.42006
Optimal Investment Strategy for Kinked Utility Maximization: Covered Call Option Strategy
Miwaka Yamashita
BlackRock Japan Co., Ltd., Tokyo, Japan
Email: Miwaka.yamashita@blackrock.com
Copyright © 2014 Miwaka Yamashita. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Miwaka Yamashita. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received October 20, 2013; revised November 29, 2013; accepted December 30, 2013
ABSTRACT
This paper describes optimal investment strategies for kinked utility functions. One example is a CRRA utility function with a kink at a maximum wealth, which leads a covered call “like” strategy and the other is a CRRA utility function with a kink at a minimum wealth, which leads a protective put “like” strategy. This paper introduces analytic mathematical solutions providing a mathematical explanation of a dual utility where Black-Sholes assumption is utilized in the solutions. The intuitive solutions are clear for cases of those kinked utilities but minute mathematical explanation is described. Also a numerical simulation is performed for a covered call like strategy case.
Keywords:
Kinked Utility; Dual Utility; Covered Call Option
1. Introduction
The modelling of problems to maximize the expected utility of end-of-period wealth by allocating wealth between a risky security and a riskless security over some investment horizon is popular among academic circles and investment practitioners. CRRA utility maximization investment strategy problems [1-5] are typical examples.
One of the ways of finding an optimal investment strategy to such a utility maximization problem is to set up the problem with a value function and Hamilton-Jacobi-Bellman (HJB) equation. However, an important condition required to use this method is that the utility function must be twice differentiable.
Recently, kinked utility maximization has been suggested as an important problem to solve. (Basic papers include [6] and examples include [7].) In these papers, corporate pension fund investment strategy problems are presented. In such cases the goal is to maximize the expected utility of end-of-period wealth by allocating wealth between a risky and riskless asset under a set of constraints. In the case of [7], the funding ratio (the ratio of total pension asset to total pension liabilities) has lower and upper limits. In this paper, these are shown to be identical with the followings. One case is that the utility function is CRRA with a kink at a minimum level of wealth. At the minimum level, the utility function goes to minus infinite. The other case is that the utility function is CRRA with a kink at a target wealth level. When the wealth is equal or larger than the target wealth level, the utility function becomes flat. [7]’s funding ratio conditions match to these utility function constraints. [6] examined that there exists a smooth classical solution to the HJB for a large class of constrained problems with utility functions that are not necessarily differentiable or strictly concave, and mathematical minutes are described based on the problem and the results match with [7].
This paper mainly treats the target wealth level case. The optimal investment strategy is to use a covered call option strategy as described in this paper. The other case is well researched and results in a protective put option strategy. Back to 1980’s, there were also discussions about if a protective put option strategy or a portfolio insurance strategy is an optimal strategy or not. [8,9] discussed about one period buying put option strategy with Black-Sholes assumption. [8] found that optimality ends to that the utility function is linear to the portfolio value and risk premium is zero. [10] found that buying put option and holding strategy is only optimal when no risk free assets exist. [11,12] solved what might be called inverse problem and examined about that given any specific dynamic strategy, can we determine whether it is self-financing, yields path-independent returns, and is consistent with optimal behaviour for some expected utility maximizing investor. [13]’s continuous time dynamic put option overlay strategy can be optimal under certain utilities and assumptions. I will also address the relationship of this paper and those discussions.
This paper consists of the following Sections. In Section 2, I set up the problem. In Section 3, I provide the details of the mathematical procedure and present the analytic solutions. In Section 4, I provide a numerical simulation example of one of the strategies presented in Section 3. In Section 5, I address about optimality discussions of option strategies. Session 6 discusses the summary and related discussions.
2. Problem Setting
2.1. The Maximization Problem
An investor’s objective is to maximize the expected utility of end-of-period (time t = T) wealth 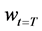 by allocating his wealth
by allocating his wealth 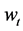 between two assets, a risky security (Risky Asset) and a riskless security (Risk Free Asset), over some investment horizon [0,T], which is called a strategy and expressed by the risky asset weight
between two assets, a risky security (Risky Asset) and a riskless security (Risk Free Asset), over some investment horizon [0,T], which is called a strategy and expressed by the risky asset weight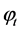 . Risky Asset’s characteristics are determined by its price S under geometric Brownian motion with drift and volatility. Using utility function
. Risky Asset’s characteristics are determined by its price S under geometric Brownian motion with drift and volatility. Using utility function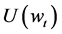 , the problem is as follows.
, the problem is as follows.
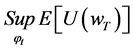 (1)
(1)
2.2. Merton Utility Function and a Utility Function with Kinks
A constant relative risk aversion utility function was used in [1], henceforth “The Merton Model”:
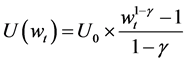 (2)
(2)
If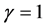 , we set logarithm function. Figure 1 depicts CRRA utility functions with
, we set logarithm function. Figure 1 depicts CRRA utility functions with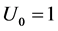 ,
, 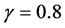 , and 1.6.
, and 1.6.
Figure 2 and Figure 3 depict the utility functions to be used in this paper. As results, Figure 2 leads to a protective put option “like” investment strategy (minimum asset level “M”) and Figure 3 leads to a covered call option “like” investment strategy. The interpretation of the Figure 3 utility function is that once the pension
Figure 1.Utility γ = 0.8 (real line), 1.6 (dot line). (The shape of the utility function. w is Asset Value. U is utility function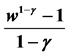 . Two lines are for γ = 0.8 case (real line) and for 1.6 case (dot line).).
. Two lines are for γ = 0.8 case (real line) and for 1.6 case (dot line).).
Figure 2. An illustration of the utility function U(w) with the kink at w = M. (U is the utility function and w is the asset value. The utility’s value goes to −∞ when w approaches the minimum asset value level “M”.) w0: initial value of w, M: minimum level, L: target level.
Figure 3.An illustration of the utility function U(w) with the kink at w = L. (U is the utility function and w is the asset value. “L” is the target level of the asset value and the utility becomes flat for w > L and w = L.). w0: initial value of w, M: minimum level, L: target level.
asset value achieves “L” (indicating its liability level) from under-funding status, the utility will not increase even if the asset value increases. In other words, achieving the full-funding level is the first priority and after that is satisfied, wealth no longer needs to be increased.
In this paper, the mathematical formation of the utility function is described by using both kinks at the minimum wealth level and the target wealth level. This is, however, not saying that the constraints are simultaneously effective. The case of both constraints is presented in the Appendix A.
2.3. Problem Setting
An objective is set to maximize the expected utility (denoting U) of end-of-period wealth 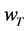 by allocating wealth
by allocating wealth 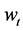 between two assets, a risky security (Risky Asset) and a riskless security (Risk Free Asset) over some investment horizon [0,T], which is called a strategy and expressed by the risky asset weight
between two assets, a risky security (Risky Asset) and a riskless security (Risk Free Asset) over some investment horizon [0,T], which is called a strategy and expressed by the risky asset weight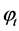 .
. 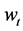 does not become 0 nor negative. Others are as follows.
does not become 0 nor negative. Others are as follows.
・ The portfolio is managed by a strategy process 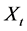 and it consists of investing in Risky Asset and Risk Free Asset.
and it consists of investing in Risky Asset and Risk Free Asset.
・ The asset amount, 
・ Risky Asset’s characteristic is set as its price S under geometric Brownian motion with drift and volatility.
Brownian motion 







The decision of the risky asset weight 






In this paper, Risky Asset’s characteristics is set as its price S is under geometric Brownian motion with drift 




Regarding Risky Asset, P-measure of 




The utility functions treated in this paper are shown in mathematical form below. Setting the CRRA utility maximization problem as follows, we denote two features of the utility function: There are kinks at the minimum level (M) and at target level (L) of asset wealth. M is for modeling of a minimum solvency level, and L is liability, which should be constant. (See Figure 2 and Figure 3.)
Mathematical expression is as follows:


(Risk averseness 
Subject to:



P: Market measure. Q: Risk neutral measure.
For the convenience, 

Again, the mathematical formation of the utility function is described by using both kinks at the minimum wealth level and the target wealth level. This is, however, not saying that the constraints are simultaneously effective.
3. The Solution Procedure
3.1. Dual Utility
Here we define the conjugate value function of 





This implies:

[14] shows 








The relationship is as follows. (The below, including


We use x and y for general variables. The maximization problem 
lows with some simplification for interception (No interception affine transform. Notation of 




(For illustrative purpose, see Figure 4 for u(x) and Figure 5 for its dual function.)
Note that 



(In
H[z] is a hebiside (step) function having value 1 only the area z and others 0.
Using Merton case (See Appendix A.) and setting the Radon-Nikodym derivative as 


and

This leads to the following:

Figure 4.







Figure 5.




3.2. Analytic Solutions
The optimal solution 







are supposing so to speak an American type option and any time arriving
to invest all money in Risk Free Asset to secure L at t = T. In such a case, 
at any time


rivative investment researches support those above. ([15,16] and etc.)
The optimal solution:

for the left side (For reference, see Figure 2), and;

for the right side (For reference, see Figure 3).
“Put(K,





3.3. Intuitive Analysis
The following presents the intuition of the solution above.
The solution (31) is a “protective put option” “like” strategy. Because the utility suddenly has negative infinite value if the pension asset value becomes below “M.” In order to avoid investor’s wealth value’s being below “M,” the solution will be to buy a put option of asset 

The solution (32) is a “covered call option” “like” strategy. Because there is no incentive to let the wealth increase once the wealth achieves the target amount “L.” The asset consists of 


The solution of the case of both constraints (lower and upper bounds) is in Appendix A.
4. Numerical Example
Using the solution of the case of a kinked utility at a maximum wealth (a covered call strategy case), I performed a Monte Carlo simulation. The solution strategy means that the investor’s wealth is under the target wealth currently (under-funding), and the strategy aims to achieve the target wealth (full-funding). In the simulation, 10,000 return patters are generated for Risky Asset’s using a geometric Brownian motion. Details of parameters are as follows. Each of the periods means one year and the total number of years is 20. As a benchmark, we denote the Merton model solution as “Standard strategy (STD).” The solution of a covered call strategy is “Covered Call strategy (CC).” A funding target “L” is exogenously given at each time. I understand CC is an optimal strategy under the kinked utility and STD is an optimal strategy under the “normal” utility, so I compare apples and oranges. However, I think it is worthwhile to compare those.
Before moving to Monte Carlo simulation results, we show the case of Risky Asset return is always constant. Figure 6 and Figure 7, and, Table 1 and Table 2 show the case of always −10% return and always +10% return respectively. 

In those, “return1” is in amount base, and “return2” is percentage base.
In the following simulations, the strategies’ actions at the beginning of period t = 1 are identical and as follows:
・ 
・ Call option strike price 63 (L0/1.596), current price 70, tenor 20,
Premium 38%, Principal amount 112 (70 × 1.596)
Initial money available = “70 + option premium 41.7” = 111.7.
・ Initial money is invested into Risky Asset 70% and Cash 30% (This background will be shown below).
Figure 6.Strategy asset value and liability value. (Risky Asset returns = −10%.) (The case of always −10% return for Risky Asset. 




Figure 7.Strategy asset value and liability value. (Risky Asset returns = +10%.) (The case of always +10% return for Risky Asset. 



The return of Risky Asset t = 1 decides which kind of call option should be sold in the CC Strategy at the beginning of period t = 2 and so forth for the full multi-period case.
In case all returns are −10%, leveraging and investing into Risky Asset (Standard portfolio
Generally speaking, a worse funding level makes 
4.1. Case 1 (Standard Case)
The following are assumptions are made:
・ Risky Asset: Return 5% p.a., Volatility 20% p.a., Brownian motion.
・ Cash: Return (risk free return) 1% p.a., Volatility 0%.
・ CC Strategy: Utility function 

・ Pension fund total asset value
・ Pension Liability
・ Total periods: 20 years.
As a benchmark strategy, STD Strategy is targeting making asset from under-funding (70) to full-funding
Table 1. Returns of risky asset are all time −10% case. Details of monte carlo simulation.
The case of always −10% return for Risky Asset. 





(100*(1 + 2%)^20) in 20 years. The expected return of STD should be 3.835%. This leads to
In CC Strategy, the underlying asset of call option is

4.2. The Simulation Results and Comparison of CC Strategy and STD Strategy
4.2.1. Return Superiority of Monte Carlo Simulation
Figure 8 shows 10,000 times Monte Carlo simulation results of total 20 years returns. The horizontal axis is STD’s full period annual return, and vertical axis is CC’s full period annual return. Dots show pair returns of (STD, CC) for 10,000 times simulation.
Table 2. Returns of risky asset are all time +10% case. Details of Monte Carlo simulation.
The case of always +10% return for Risky Asset. 




CC Strategy shows that its return has a 3.856% cap (upper limit). This means that the strategy’s aim is achieve a funding level of 100%, and the 3.835% return is enough. (As described before, the 3.835% return makes the funding level from 70% to 100% based on 2% p.a. liability increase for 20 years.) The possibility of a final return of CC is better than STD is almost every case. But, there is an effect of additional return especially if STD’s return is negative.
In addition to the full 20-year results, Figure 9 shows 5 years later and 10 years later interim results.
The shape tends to become covered call type payoff.
4.2.2. Distribution of Returns
Figure 10 shows 10,000 times Monte Carlo simulation return distribution results.
Figure 8. Comparison of CC Strategy and STD Strategy. (This shows 10,000 times Monte Carlo simulation results of total 20 years returns. The horizontal axis is Standard Strategy (STD)’s full period annual return, and vertical axis is Covered Call Strategy (CC)’s full period annual return. Dots show pair returns of (STD, CC) for 10,000 times simulation. The 45 degree line shows CC return = STD return.)
Figure 9. 5 years period (up), 10 years period (down). (This shows 5 years later and 10 years later interim results with the same setting of the case of Figure 8, where the result of the full 20-year case is shown. These also show 10,000 times Monte Carlo simulation results. The horizontal axis is Standard Strategy (STD)’s full period annual return, and vertical axis is Covered Call Strategy (CC)’s full period annual return. Dots show pair returns of (STD, CC) for 10,000 times simulation. The 45 degree line shows CC return = STD return.)
CC Strategy return distribution shows that both fewer big positive return and fewer big negative return arise.
4.2.3. Volatility Distribution
CC has a smaller and more narrowly distributed volatility as shown in Figure 11.
The following summarize the CC Strategy characteristics:
・ Full period total return of the CC Strategy and STD Strategy look like the same, but the CC Strategy has downside resistance, meaning superior returns especially when STD Strategy has negative returns.
・ According to the Monte Carlo simulation, the CC Strategy has fewer negative and more positive return opportunities.
・ Volatility of the CC Strategy is very small on average.
4.3. Sensitivity of the Simulation
Setting parameters differently versus Case 1, I checked the sensitivity of the volatility increase and expected return improvement. Table 3 shows those new parameters. The return distribution is shown in Figure 12.
This sensitivity analysis shows the following:
・ In Table 3, you see the ratio of CC to STD is superior by 46.5% (almost half and half) in Case 1. Case 3 is higher volatility of Risky Asset and the ratio of Case 3 is as large as 58.9%. Instead, in Case 2, which is the smaller volatility case, the ratio is only 19.3%.
・ In case of a higher expected return of Risky Asset (Case 5), we see the ratio is 30.3% and in case of a smaller expected return, we see the ratio is 67.5%.
Therefore, the following observations can be made:
・ Reducing volatility makes less risk averse and less cash position. As a result, portfolio volatility increases and the premium earned by covered call increases.
・ Increasing volatility makes more risk averse and more cash position. As a result, portfolio volatility decreases and the Covered Call effect decreases.
・ In case expected return decreases, more Risky Asset ratio makes more Covered Call merit.
Figure 10. Return distribution of CC Strategy and STD Strategy. (This shows 10,000 times Monte Carlo simulation return distribution results. Covered Call (CC) Strategy return distribution shows that both fewer big positive return and fewer big negative return arise than that of Standard (STD) Strategy.)
Figure 11. Volatility distribution of CC Strategy and STD Strategy. (This shows 10,000 times Monte Carlo simulation return’s volatility distribution results. Covered Call (CC) Strategy has a smaller and more narrowly distributed volatility than Standard (STD) Strategy.)
Table 3. Parameters of simulations and results.
This shows 10,000 times Monte Carlo simulation results of total 20 years returns like Figure 8. Several cases of the parameters of drift and volatility are tested. The upper part of the table shows parameters. The middle part of the table shows characteristics. The bottom part of the table shows the results of the comparison for several cases. The ratios of simulation results, which shows Covered Call Strategy (CC) is superior to Standard Strategy (STD) regarding the end of returns (the end of asset values), are shown.
5. Relation with the Optimality of Option Strategies
In Section 1, I introduced previous works about portfolio insurance and put option optimality discussions. Although works of [11-13] and this paper treat dynamic strategy meaning not buying and holding strategies nor one period models, this Section starts one period model discussion of [8,10].
Actually, regarding [8], the model supposing the risk neutral measure of Black-Sholes type, a CRRA utility function, and a geometric Brownian motion for a risky asset return, finds a myopic strategy. In addition, it shows as same characteristics as one period model. Using this paper’s notation (Appendix B, portfolio





Figure 12. Case2, Case 3, Case 4 and Case 5 Comparison of CC Strategy and STD Strategy of Monte Carlo simulation return. (This shows 10,000 times Monte Carlo simulation results of total 20 years returns like Figure 8 but several cases of the parameters of drift and volatility are tested. The horizontal axis is Standard Strategy (STD)’s full period annual return, and vertical axis is Covered Call Strategy (CC)’s full period annual return. Dots show pair returns of (STD, CC) for 10,000 times simulation. Parameters are in Table 3.) (From Top Left Case 2, Top Right Case 3, Bottom Left Case 4, Bottom Right Case 5).




They discussed that above (35) indicates that risk premium should be zero and this turns out with (36) that the utility function U is a linear function. Figure 13 illustrates this. Here our model solution for protective put type strategy varies its strike price and its amount of option time to time. This fill the gap between the difference of utility functions of Figure 2 and Figure 13.
[10]’s discussion is put option buying and holding optimality. Using this paper’s notation, with a CRRA utility function and Black-Sholes assumption, they can indicate the risk averseness 

In their case, they set 
With our model, [13]’s discussion is more relevant than that of [11,12]. (The latter discusses with outflow and some more general strategies.) [13] showed optimality of the Option Based Portfolio Insurance method. We set a scalar 

6. Summary and Related Discussions
For an investment strategy with a smooth utility function, the Merton model solution is obtained under strict conditions that the utility function is differentiable and strictly concave. When [7] set constraints or an adjusted
Figure 13. An illustration of the utility function U(w). Because of convex shape, the utility function’s value goes to ?¥ when approaches the minimum asset value level “M.”
utility function, such as once the pension asset value achieves “L (indicating its liability level)” from under-funding status, the utility will not increase as even though the asset value increases, and the Merton conditions are not satisfied.
This paper described optimal investment strategies for kinked utility functions like CRRA utility function with a kink at a maximum wealth. The solutions are analytic mathematical solutions, one of which expresses a covered call option “like” strategy with dynamically managed and the option parameter varies. The other is a protective put option “like” strategy with dynamically managed and the option parameter varies. Dual utility with a Black-Sholes assumption is utilized in the solutions.
Some related discussions are described. For generally, non-smooth and/or non-strictly-concave utility functions, it is not clear if there exist smooth solutions to the HJB. To deal with the lack of a priori knowledge of the differentiability of the value function one may use a weak solution concept and characterize the value function as a unique viscosity solution to the HJB ([17-21] and etc.). It is in general difficult to show the differentiability of the value function even it is known to be a viscosity solution to the HJB. The lack of the differentiability of the value function makes it impossible to apply the verification theorem to find the optimal control. Another related issue is the Backward Stochastic Differential equations ([22] and etc.). Future work should involve solving the problem regarding those points.
Finally, the following summarize the numerical simulations for the Merton model strategy (STD) and the covered call strategy (CC) described above.
・ Full period total return of the CC Strategy and STD Strategy look the same, but the CC Strategy has downside resistance, meaning superior returns especially when the STD Strategy has negative returns.
・ According to the Monte Carlo simulation, the CC Strategy has fewer negative and more positive return opportunities.
・ Volatility of CC Strategy is very small on average.
・ The CC Strategy merit will increase if volatility increases but the merit decreases if expected return increases.
References
- 1. R. C. Merton, “Optimum Consumption and Portfolio Rules in a Continuous-Time Model,” Journal of Economic Theory, Vol. 3, No. 4, 1971, pp. 373-413. http://dx.doi.org/10.1016/0022-0531(71)90038-X
- 2. R. C. Merton, “Continuous-Time Finance,” Blackwell Publishers, Oxford, 1992.
- 3. R. C. Merton, “Lifetime Portfolio Selection under Uncertainty: The Continuous-Time Case,” Review of Economics and Statistics, Vol. 51, No. 3, 1969, pp. 247-257. http://dx.doi.org/10.2307/1926560
- 4. R. C. Merton, “Optimum Consumption and Portfolio Rules in a Continuous-Time Model,” Journal of Economic Theory, Erratum, Vol. 6, No. 2, 1973, pp. 213-214.
- 5. J. C. Cox and C.-F. Huang,”Optimal Consumption and Portfolio Policies When Asset Prices Follow a Diffution Process,” Journal of Economic Theory, Vol. 49, No. 1, 1987, pp. 33-83.
http://dx.doi.org/10.1016/0022-0531(89)90067-7 - 6. B. Bian, S. Miao and H. Zheng, “Smooth Value Functions for a Class of Nonsmooth Utility Maximization Problems,” SIAM Journal of Financial Mathematics, Vol. 2, 2011, pp. 727-747.
- 7. L. Martellini and V. Milhau, “Dynamic Allocation Decisions in the Presence of Funding Ratio Constraints,” Working Paper of EDHEC, Roubaix, 2009.
- 8. M. J. Brennan and R. Solanki, “Optimal Portfolio Insurance,” The Journal of Financial and Quantitative Analysis, Vol. 16, No. 3, 1981, pp. 279-300. http://dx.doi.org/10.2307/2330239
- 9. H. E. Leland, “Who Should Buy Portfolio Insurance?” The Journal of Finance, Vol. 35, No. 2, 1980, pp. 581-594.
- 10. S. Benninga and M. Blume, “On the Optimality of Portfolio Insurance,” The Journal of Finance, Vol. 40, No. 5, 1985, pp. 1314-1352. http://dx.doi.org/10.1111/j.1540-6261.1985.tb02386.x
- 11. J. C. Cox and H. E. Leland, “On Dynamic Investment Strategies,” In: Proceedings of the Seminar on the Analysis of Securities Prices, Center for Research in Security Prices (CRSP), Chicago, 1982, pp. 139-173.
- 12. J. C. Cox and H. E. Leland, “On Dynamic Investment Strategies,” Journal of Economic Dynamics and Control, Vol. 24, No. 11-12, 2000, pp. 1859-1880. http://dx.doi.org/10.1016/S0165-1889(99)00095-0
- 13. N. El Karoui, M. Jeanblanc and V. Lacoste, “Optimal Portfolio Management with American Capital Guarantee,” Journal of Economic Dynamics and Control, Vol. 29, No. 3, 2005, pp. 449-468.
http://dx.doi.org/10.1016/j.jedc.2003.11.005 - 14. W. Schachermayer, “Optimal Investment in Incomplete Markets When Wealth May Become Negative,” The Annals of Applied Probability, Vol. 11, No. 3, 2001, pp. 694-734.
http://dx.doi.org/10.1214/aoap/1015345346 - 15. P. Carr and D. Madan, “Optimal Positioning in Derivative Securities,” Quantitative Finance, Vol. 1, No. 1, 2001, pp. 19-37.
http://dx.doi.org/10.1080/713665549 - 16. J.-L. Prigent and F. Tahar, “Optimal Portfolios with Guarantee at Maturity: Computation and Comparison,” International Journal of Business, Vol. 11, No. 2, 2006, pp. 171-185.
- 17. L. T. Ndounkew, “Stochastic Control: With Applications to Financial Mathematics,” African Institute for Mathematical Sciences Postgraduate Diploma, Muizenberg, 2010.
- 18. H. Pham, “On Some Recent Aspects of Stochastic Control and Their Applications,” Probability Surveys, Vol. 2, No. 2005, 2005, pp. 506-549. http://dx.doi.org/10.1214/154957805100000195
- 19. H. Pham, “Stochastic Control and Applications in Finance,” Lecture Note, Paris Diderot University, LPMA, Paris, 2010.
- 20. J. Sass, “Stochastic Control: With Applications to Financial Mathematics,” Working Paper, Austrian Academy of Sciences, Vienna, 2006.
- 21. J. Sekine, “Long-Term Optimal Portfolios with Floor,” Finance and Stochastics, Vol. 16, No. 3, 2012, pp. 369-401.
- 22. N. El Karoui, S. Peng and M. C. Quenez, “Backward Stochastic Differential Equations in Finance,” Mathematical Finance, Vol. 7, No. 1, 1997, pp. 1-71. http://dx.doi.org/10.1111/1467-9965.00022




















