Journal of Mathematical Finance
Vol.3 No.3A(2013), Article ID:37582,8 pages DOI:10.4236/jmf.2013.33A001
Valuation and Financing of Cash Cows and Growth Firms
1School of Management, State University of New York at Buffalo, Buffalo, USA
2College of Business, University of Arkansas at Fort Smith, Fort Smith, USA
Email: *joeogden@buffalo.edu, Sharon.Wu@uafs.edu
Copyright © 2013 Joseph P. Ogden, Shanhong Wu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 13, 2013; revised September 14, 2013; accepted September 26, 2013
Keywords: Valuation; Financing; Agency Costs; Trade-Off Theory
ABSTRACT
This paper develops separate trade-off models for the valuation and financing of non-growth firms (cash cows) and growth firms that incorporate tax benefits, bankruptcy costs, and relevant agency costs. Cash cows generally have relatively high leverage, though firm value, leverage, and profitability are all affected by variations in the efficacy of both internal and external governance mechanisms to mitigate agency costs of managerial discretion. For growth firms, where agency costs of debt are relevant, we find that: 1) optimal leverage is generally relatively low; 2) the relationship between optimal leverage and Tobin’s Q is negative and highly convex; and 3) optimal leverage increases with initial profitability. Our analysis helps to explain anomalous results documented in previous empirical tests of trade-off theory, specifically, relationships between leverage and both the market-to-book assets ratio and profitability.
1. Introduction
In a perfect market, the value of a firm is independent of its capital structure [1]. Leverage is relevant to firm value, however, in the presence of market imperfections. In the traditional trade-off theory of capital structure, each firm has a unique optimal (i.e., firm value-maximizing) leverage ratio that balances the tax benefit of interest deductibility against the present value of expected deadweight costs of future financial distress and bankruptcy, both of which increase with leverage [2]. Empirical evidence based on leverage regressions in [3-5] and many other studies is generally consistent with the traditional trade-off theory, with two notable anomalies. First, leverage is found to be negatively, rather than positively, related to profitability. Second, while the coefficient of the market-to-book assets ratio (MB), a proxy for Tobin’s Q ratio [6] and a measure of growth opportunities, is negative as expected, and the explanatory power of MB is low. However, in a recent paper, Ogden and Wu [5] find that the relationship between leverage and MB is strong when it is recognized that the relationship is highly convex.
The leverage decision is particularly complex when we consider two types of agency costs. The first is agency costs of managerial discretion, which are relevant for a “cash cow;” that is, a profitable firm with no growth options. Managers of cash cows have an incentive to capture the firm’s free cash flow as a private benefit rather than distribute it to shareholders. To the extent that managers can capture free cash flow, profitability and firm value are reduced. In this situation, debt increases firm value by forcing the disgorgement of free cash flow. The question we address here is whether, and the extent to which, agency costs of managerial discretion will be mitigated by bringing to bear internal and/or external governance mechanisms that impose debt on management [7-12].
The second source of agency costs pertains to growth firms; i.e., firms that have options for profitable future investment. Debt is inherently problematic for such firms because it entails conflicts of interest between shareholders and debtholders. Specifically, management, acting in the shareholders’ interest, will tend to underinvest in growth options because much of the benefit of investment will passively accrue to existing debtholders. Hence, for growth firms debt entails deadweight costs. The circumstance is known as the underinvestment, or debt overhang, problem [13]. The question we address here is whether, and the extent to which, underinvestment costs inhibit the use of debt despite the tax benefit.
To address these issues, we develop separate models for the valuation and financing of cash cows and growth firms that incorporate tax benefits, bankruptcy costs, and relevant agency costs. Our focus is on how trade-offs among these benefits and costs affect firm value and leverage for each firm type. Our models are adaptations of previously-developed valuation/financing paradigms [14, 15]. Our model for cash cows allows for variation in the efficacy of both internal and external governance mechanisms to mitigate agency costs of managerial discretion. For growth firms, our model allows for short-term debt to mitigate agency costs of debt. For both models we use empirically relevant parameter values to develop simulation estimates.
For cash cows, our analysis yields several important and novel findings. First, leverage for cash cows is relatively high even when agency costs of managerial discretion are high. Second, the relationship between leverage and the severity of agency costs of managerial discretion is complex, depending on the efficacy of both internal and external governance mechanisms. Third and fourth, one interpretation of the results implies negative relationships between leverage and both Q and profitability, driven by cross-sectional variation in takeover costs. These results provide novel explanations for negative relationships between leverage and both MB and profitability found empirically, though the results apply only to cash cows.
For growth firms, our model generates the following simulation results. First, optimal leverage is generally relatively low. Second, the relationship between optimal leverage and Q is negative and highly convex, consistent with evidence in [5]. Third, optimal leverage increases with initial profitability.
Overall, our results have implications for empirical studies of trade-off theory. In particular, results suggest that relationships between leverage and both MB and profitability are likely complex in samples that include both cash cows and growth firms.
Our paper relates to a large literature that models the effects of agency costs of managerial discretion and/or of debt on firm value and financing. Our paper relates most closely to the following previous studies. Stulz [9] focuses on agency costs of managerial discretion that arise because management derives perquisites from investment and so invests as much as possible. However, shareholders retain control rights over financing policy, and so can impose debt on management, which reduced agency costs. Optimal leverage, determined by shareholders, minimizes investment distortions. The model in [9] ignores agency costs of debt and does not include a mechanism for a hostile takeover.
Barclay et al.’s [16] model incorporates agency costs of both managerial discretion and debt, where the former (latter) decreases (increases) with additional growth options. The firm’s board of directors has control rights over financing policy, and thus optimal leverage is determined ex ante to maximize firm value. Importantly, [16] shows that growth options have negative debt capacity.
Hackbarth and Mauer [14] analyze the investment and financing decisions of growth firms. The firm can have multiple debt issues, and the debt issues can vary in terms of priority. Their primary focus is on how future investment is financed. They find that jointly optimal capital and priority structures can eliminate investment distortions because debt priority serves as a dynamically optimal contract. All debt issues in their model have infinite maturity (i.e., are perpetual).
Finally, Morellec et al. [15] focus on the effects of manager-shareholder conflicts, as well as taxes and distress costs, on capital structure. Managers own a fraction of the firms’ equity and capture part of free cash flow to equity as a private benefit. The latter benefit is restricted by a governance mechanism, and variation in the efficacy of this mechanism is a key aspect of their analysis. Managers have control rights over the firm’s financing policies, and management sets leverage to maximize the value of its overall stake in the firm. In general, they find that conflicts between managers and shareholders reduce the firm’s leverage, though the extent to which this occurs depends critically on the aforementioned governance mechanism.
The remainder of the paper is organized as follows. In Section 2, we develop models for the valuation and financing of cash cows under various circumstances with regard to agency costs of managerial discretion, and generate simulated numerical estimates. In Section 3, we develop a model for the valuation and financing of a growth firm with emphasis on the effect of agency costs of debt on optimal leverage, and develop simulated numerical estimates. Section 4 summarizes.
2. Valuation and Financing of a Cash Cow
2.1. General Setting
A cash cow has initial assets-in-place, A0, that generate earnings before interest and taxes (EBIT) of Xt at time t, where Xt follows geometric Brownian motion with initial value , drift of μ (risk neutral drift of EBIT flow rate), and volatility σ under the risk neutral measure. Thus,
, drift of μ (risk neutral drift of EBIT flow rate), and volatility σ under the risk neutral measure. Thus,
 (2.1)
(2.1)
where μ and σ are constants and dz is the increment of a standard geometric Brownian motion. A risk-free technology exists that yields a rate of  per unit time, and
per unit time, and . The firm pays corporate taxes at a constant rate τ. Under these circumstances it is well known that the value of an unlevered cash cow, VUCC, is
. The firm pays corporate taxes at a constant rate τ. Under these circumstances it is well known that the value of an unlevered cash cow, VUCC, is
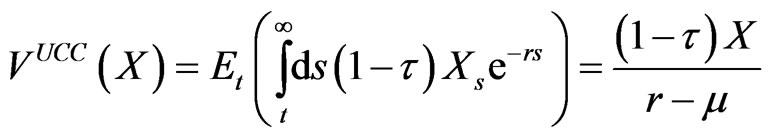 . (2.2)
. (2.2)
2.2. No Agency Cost Case
Initially we consider the valuation and financing of a cash cow in the absence of agency costs of managerial discretion. Management receives only “normal” compensation, which is incorporated into Xt, and selects the initial capital structure that maximizes firm value. Management may be able to increase firm value beyond VUCC by issuing perpetual debt with a coupon payment of C (proceeds of which are distributed to shareholders) because coupon payments are deductible and thus generate an interest tax shield of τC outside bankruptcy. However, in the event of bankruptcy shareholders receive nothing and bondholders receive the firm’s assets net of bankruptcy costs, where bankruptcy costs include the loss of the interest tax shield and the fraction α of assets-inplace.
2.2.1. The Model
Under the conditions specified above, the value of the cash cow as a levered firm, VLCC, will differ from its unlevered value, VUCC given in (2.2), according to the effects of both tax benefits and bankruptcy costs associated with debt. Our derivation of VLCC follows [14]. Key to the derivation is the value of X that triggers default, denoted as . Default is determined by management to maximize the value of the firm’s levered equity, ELCC, specified below. Hence, ELCC must satisfy a smooth-pasting condition [17] at the default threshold,
. Default is determined by management to maximize the value of the firm’s levered equity, ELCC, specified below. Hence, ELCC must satisfy a smooth-pasting condition [17] at the default threshold,
 . This condition is used to determine the value of Xdh:
. This condition is used to determine the value of Xdh:
 , (2.3)
, (2.3)
where  is the negative root of the quadratic equation
is the negative root of the quadratic equation .
.
The value of the levered cash cow is then
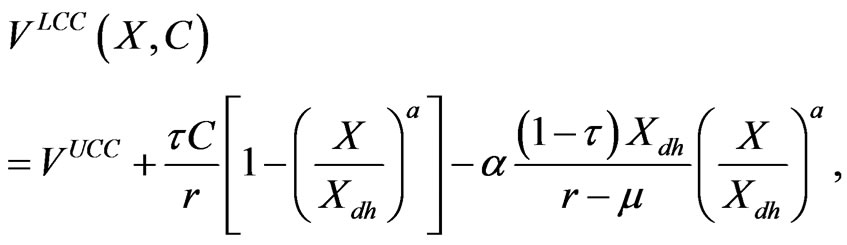 (2.4)
(2.4)
where the ratio  is the value of a contingent claim paying $1 if X hits Xdh the first time from above. The second term in (2.4) is the present value of the interest tax shield, and the third term is the present value of bankruptcy costs. Management chooses C to maximize VLCC. An interior optimal leverage level is possible depending on values of the various parameters.
is the value of a contingent claim paying $1 if X hits Xdh the first time from above. The second term in (2.4) is the present value of the interest tax shield, and the third term is the present value of bankruptcy costs. Management chooses C to maximize VLCC. An interior optimal leverage level is possible depending on values of the various parameters.
The values of the cash cow’s levered debt and equity, DLCC and ELCC are, respectively:
 (2.5)
(2.5)
and
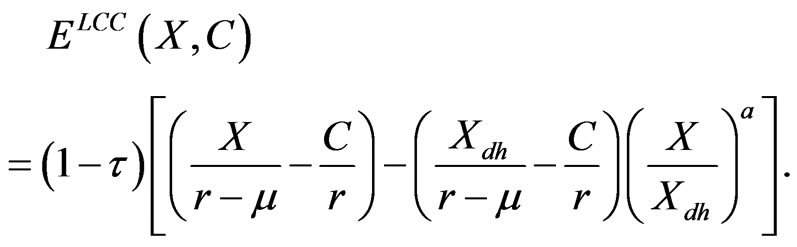 (2.6))
(2.6))
Finally, from inspection it is clear that (2.5) and (2.6) reconcile with (2.4); that is:
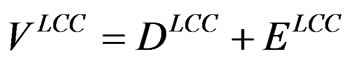 . (2.7)
. (2.7)
2.2.2. Numerical Estimates
To obtain numerical estimates for the value and optimal leverage of a cash cow in this case, we use the following parameter values, which are empirically relevant and similar to the base values used in [14]: ; σ = 25%;
; σ = 25%; ;
; ; and
; and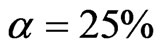 . The initial value of assets-in-place is A0 = 100, and the initial pre-tax cash flow, X0, is set to
. The initial value of assets-in-place is A0 = 100, and the initial pre-tax cash flow, X0, is set to 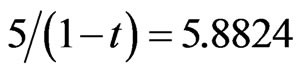 so that the value of the cash cow with no leverage,
so that the value of the cash cow with no leverage, 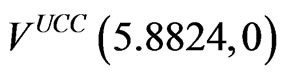 , is 100, and thus the value of its Tobin’s Q ratio is
, is 100, and thus the value of its Tobin’s Q ratio is  . By doing so, we can use Q to assess the effect of leverage on firm value relative to this “null” Q value of 1.0, for both the cash cow and, later, a growth firm. For the chosen parameter values, at optimal leverage firm value is
. By doing so, we can use Q to assess the effect of leverage on firm value relative to this “null” Q value of 1.0, for both the cash cow and, later, a growth firm. For the chosen parameter values, at optimal leverage firm value is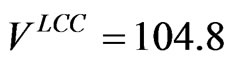 , leverage is
, leverage is 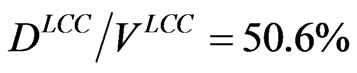 , and
, and . Thus, at optimal leverage firm value is about 5% higher than its no-leverage value, consistent with empirical estimates in [18].
. Thus, at optimal leverage firm value is about 5% higher than its no-leverage value, consistent with empirical estimates in [18].
2.3. Agency Cost Case
Agency costs of managerial discretion arise when shareholders, or more precisely the firm’s board of directors, have limited capability to discipline managers. However, managers may also disciplined by the external market for corporate control (i.e., the potential for a hostile takeover), though this external governance mechanism may be limited as well. Given discretion, management captures economic rents, which reduce firm value. The leveragedecision is also more complex in this setting. Our cash cow model with agency costs focuses on these factors.
2.3.1. The Model
To incorporate agency costs of managerial discretion, we adopt the following assumptions: 1) Management receives “normal” compensation (incorporated into Xt) plus economic rents in the form of the fraction γ of the firm’s free cash flow, 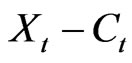 , as a cash payment; 2) The firm can deduct the payment of
, as a cash payment; 2) The firm can deduct the payment of  for tax purposes; and 3) Management loses all economic rents in the event of bankruptcy. Under these assumptions, and initially ignoring the external governance mechanism, the present value of management’s economic rents, and thus the present value of agency costs, denoted as
for tax purposes; and 3) Management loses all economic rents in the event of bankruptcy. Under these assumptions, and initially ignoring the external governance mechanism, the present value of management’s economic rents, and thus the present value of agency costs, denoted as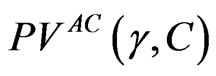 , is:
, is:
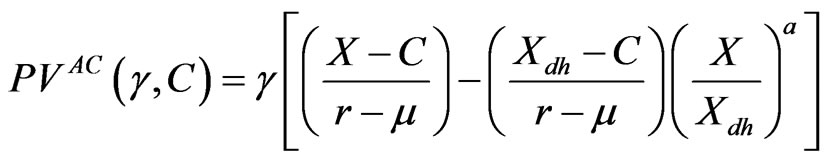 . (2.8)
. (2.8)
Thus, the value of a cash cow with agency costs, denoted as , is:
, is:
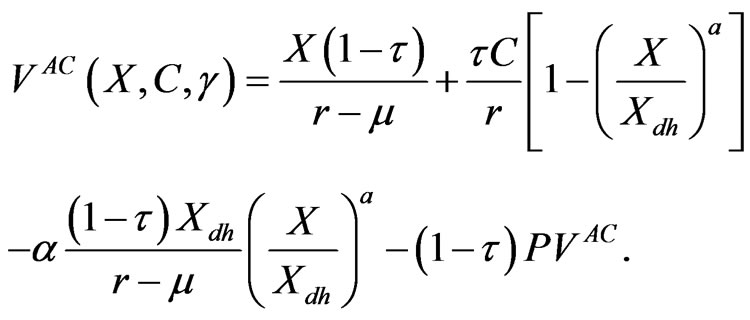 (2.9)
(2.9)
We also assume that management seeks to maximize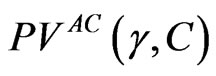 . This situation gives rise to several scenarios that are differentiated in terms of management’s control rights. In the first scenario (which may be the least realistic), management has discretion over the firm’s debt policy and does not face the threat of a hostile takeover. From (2.8) and for any given level of γ, management would clearly choose no leverage (i.e., C = 0), despite the (net) tax benefit of debt for the firm.
. This situation gives rise to several scenarios that are differentiated in terms of management’s control rights. In the first scenario (which may be the least realistic), management has discretion over the firm’s debt policy and does not face the threat of a hostile takeover. From (2.8) and for any given level of γ, management would clearly choose no leverage (i.e., C = 0), despite the (net) tax benefit of debt for the firm.
In the second scenario, management retains discretion over debt policy; however, management faces the threat of a hostile takeover. In a hostile takeover, an outside investor group purchases the entire firm at the price of VAC, incumbent management is fired, and new owners run the firm according to (2.4), i.e., without agency costs and using optimal leverage. Thus, gross profit from the deal for the new owners, expressed in percentage terms, is . A hostile takeover is costly, however, so outsiders would pursue it only if G exceeds a takeover threshold value denoted as TT. Under these circumstances, incumbent management would choose the combination of γ and C that maximizes
. A hostile takeover is costly, however, so outsiders would pursue it only if G exceeds a takeover threshold value denoted as TT. Under these circumstances, incumbent management would choose the combination of γ and C that maximizes 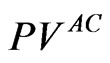 subject to the constraint that
subject to the constraint that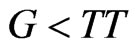 . Consequently, even though incumbent management has complete discretion over leverage, under these circumstances they would not necessarily choose zero leverage because the (net) tax benefit of leverage adds to firm value
. Consequently, even though incumbent management has complete discretion over leverage, under these circumstances they would not necessarily choose zero leverage because the (net) tax benefit of leverage adds to firm value 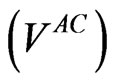 and therefore contributes to satisfying the constraint
and therefore contributes to satisfying the constraint .
.
In the third and final scenario, management has the least control rights: The firm’s board has decision rights over financing policy, and management faces the threat of a hostile takeover. The board, acting in shareholders’ interest, chooses the level of leverage that maximizes firm value, given γ. Meanwhile, management chooses γ to maximize  subject to the conditions that: 1) The board will respond with the aforementioned level of leverage; and 2)
subject to the conditions that: 1) The board will respond with the aforementioned level of leverage; and 2)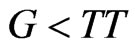 .
.
2.3.2. Numerical Estimates
We generate numerical estimates of firm value and leverage for the second and third scenarios above. For each scenario we use previously specified parameter values ( ;
;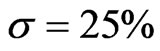 ;
;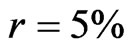 ;
; ;
; ; and
; and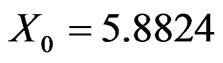 ) and the following alternative values of the takeover threshold variable TT: 0.0%, 1.5%, 3.0%, 6.0%, 12.0%, and 24.0%. Note that for TT = 0.0% the situation reverts to the no-agency cost optimization problem of (2.4); i.e., with
) and the following alternative values of the takeover threshold variable TT: 0.0%, 1.5%, 3.0%, 6.0%, 12.0%, and 24.0%. Note that for TT = 0.0% the situation reverts to the no-agency cost optimization problem of (2.4); i.e., with  management cannot capture economic rents.
management cannot capture economic rents.
For the second (third) scenario and each value of , we identify the level of leverage that management (the board) chooses to maximize
, we identify the level of leverage that management (the board) chooses to maximize  (
( , given γ). Specifically, for both scenarios the solution must satisfy smooth-pasting conditions. For the second scenario, the smooth-pasting conditions are:
, given γ). Specifically, for both scenarios the solution must satisfy smooth-pasting conditions. For the second scenario, the smooth-pasting conditions are:
 . (2.10)
. (2.10)
For the third scenario, the smooth-pasting conditions are:
 . (2.11)
. (2.11)
Results are displayed in Figure 1. The figure shows plots of Q-leverage combinations for each value of TT. The upper-most series of plots, corresponding to TT = 0.0%, reflect only the traditional trade-off between tax benefits and bankruptcy costs because, as noted above, with TT = 0.0% management cannot capture economicrents. The point corresponding to firm value maximization is indicated with the enlarged marker “X,” which corresponds to values reported earlier for the no-agency cost case; i.e., optimal leverage is 50.6% and . Regarding the other series, note initially that Q (or equivalently, firm value) falls as TT rises for each leverage level because management can increase γ as TT increases.
. Regarding the other series, note initially that Q (or equivalently, firm value) falls as TT rises for each leverage level because management can increase γ as TT increases.
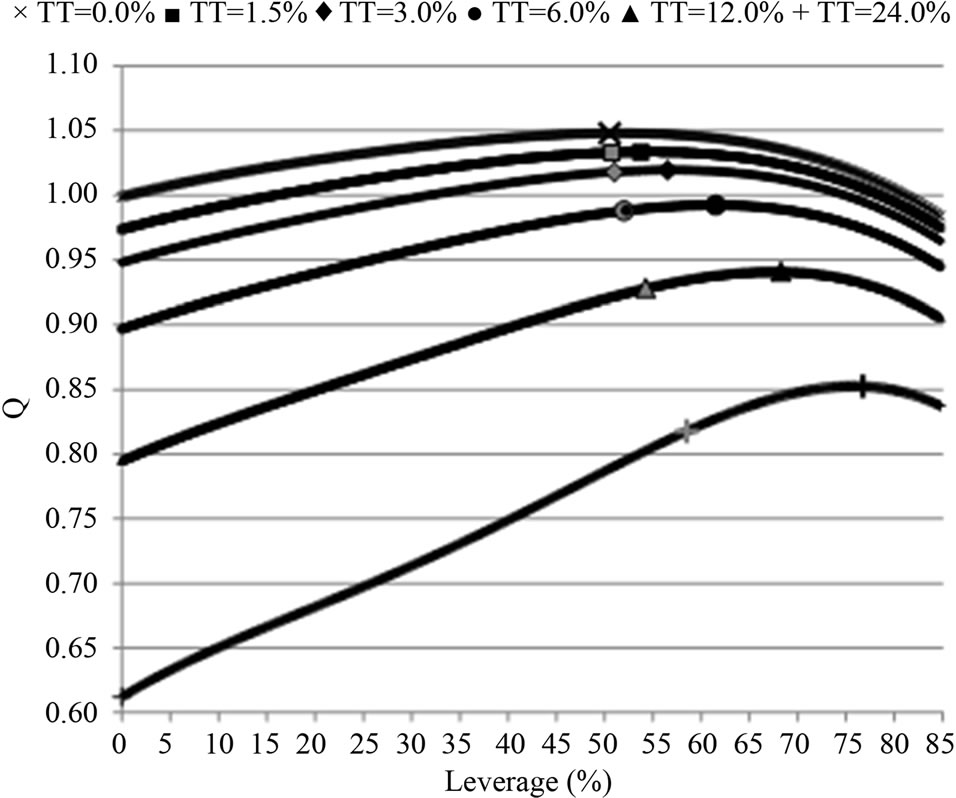
Figure 1. Valuation and financing of cash cows.
Next we focus on leverage levels that result from management’s optimization in the second scenario (i.e., choose γ and C to maximize PVAC subject to G < TT). For each value of TT the management-optimal Q-leverage combination is depicted with an enlarged gray-scale marker. Management-chosen leverage actually increases modestly with TT, from 51.2% for 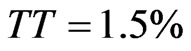 to 56.6% for
to 56.6% for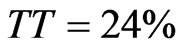 . It may seem counterintuitive that management would choose to increase, rather than decrease, leverage as TT increases. However, as noted earlier management will employ leverage because the (net) tax benefit adds to firm value
. It may seem counterintuitive that management would choose to increase, rather than decrease, leverage as TT increases. However, as noted earlier management will employ leverage because the (net) tax benefit adds to firm value 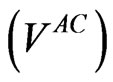 and therefore contributes to satisfying the constraint
and therefore contributes to satisfying the constraint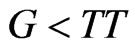 .
.
Finally, we discuss values that result from the third scenario. Here the board chooses leverage to maximize VAC in response to management’s choice of γ, which in turn management chooses based on both TT and the board’s leverage-response mechanism. For each value of TT the resulting “optimal” Q-leverage combination is depicted with an enlarged black marker. Board-chosen optimal leverage increases with TT, ranging from 53.75% for 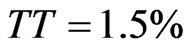 to 76.75% for
to 76.75% for . These results have a straight-forward interpretation: An increase in TT represents a weakening of the external governance mechanism, which allows management to increase its private benefits (i.e., γ), and the board responds by increasing leverage. In addition, for each value of
. These results have a straight-forward interpretation: An increase in TT represents a weakening of the external governance mechanism, which allows management to increase its private benefits (i.e., γ), and the board responds by increasing leverage. In addition, for each value of , Q is higher in the third scenario than the second scenario, reflecting the benefit to shareholders of having the board, rather than management, control the leverage decision.
, Q is higher in the third scenario than the second scenario, reflecting the benefit to shareholders of having the board, rather than management, control the leverage decision.
The results in Figure 1 have several important implications for empirical analysis. First, the relationship between leverage and the severity of agency costs of managerial discretion is complex, depending on the efficacy of both internal and external governance mechanisms. This may explain why in their empirical study Berger et al.
[19] find no relationship between market leverage and excess CEO compensation even as they find positive relationships between market leverage and measures of governance strength; e.g., the presence of a blockholder and the percentage of board directors who are outsiders (see their Table II).
Second, for cash cows the relationship between leverage and Q is also potentially complex. On one hand, if either the second or third scenario holds universally (i.e., for all individual firms either management or the board controls debt policy), then the results in Figure 1 suggest a negative relationship between leverage and Q, driven by cross-sectional variation in takeover costs (TT). As noted earlier, empirical studies consistently find a negative relationship between leverage and MB. However, the general explanation for this relationship is that MB is a measure of growth options, and optimal leverage is negatively related to growth options, as shown in [14,16] and in Section 3. Results in Figure 1, as interpreted, are important because they suggest an alternative reason for the negative leverage-MB relationship, although this explanation applies only to cash cows. On the other hand, if we hold TT constant then the results in Figure 1 suggest a positive relationship between leverage and Q for cash cows, driven by cross-sectional variation in control rights over debt policy (management vs. the board).
Third and finally, the results in Figure 1 also suggest that the relationship between leverage and profitability is complex. Though profitability is not explicitly shown in Figure 1, it is negatively related to management’s ability to capture economic rents. Thus, for either the second or third scenario profitability and Q fall, and leverage rises, as TT rises. As noted earlier, empirical studies consistently find a negative relationship between market leverage and profitability. This relationship is considered to be anomalous because, according to trade-off theory, more profitable firms face higher taxes (and also a lower probability of bankruptcy), and thus should make more use of leverage as a tax shield. A common explanation for the anomaly is that positive (negative) profit “shocks” cause a firm’s leverage to be temporarily low (high), and firms adjust to profit shocks only on a delayed basis [3]. Our analysis provides the aforementioned alternative explanation, though it applies only to cash cows and to the extent that takeover costs vary cross-sectionally. On the other hand, if TT is fixed then Figure 1 suggests a positive relationship between leverage and profitability for cash cows, driven by cross-sectional variation in control rights over debt policy (management vs. the board).
3. Valuation and Financing of a Growth Firm
3.1. General Setting
Our setting for the valuation and financing of a growth firm is as follows. Like the cash cow, the firm has initial assets-in-place, A0, that generate earnings before interest and taxes (EBIT) of Xt at time t, where Xt follows geometric Brownian motion with initial value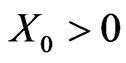 , drift of m, and volatility s under the risk-neutral measure. A risk-free technology exists that yields a rate of
, drift of m, and volatility s under the risk-neutral measure. A risk-free technology exists that yields a rate of 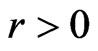 per unit time. The firm pays corporate taxes at a constant rate t and interest on debt is deductible. Unlike the cash cow, however, the growth firm also has growth options, henceforth GOs, that can be exercised at a future date T, after which the firm reverts to cash cow status with stochastic EBIT that incorporates exercised GOs. The firm’s post-investment EBIT,
per unit time. The firm pays corporate taxes at a constant rate t and interest on debt is deductible. Unlike the cash cow, however, the growth firm also has growth options, henceforth GOs, that can be exercised at a future date T, after which the firm reverts to cash cow status with stochastic EBIT that incorporates exercised GOs. The firm’s post-investment EBIT, 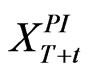 , follows geometric Brownian motion with initial value
, follows geometric Brownian motion with initial value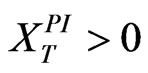 , drift of m, and volatility s under the risk-neutral measure, and assumptions about r, t, and interest deductibility continue to hold.
, drift of m, and volatility s under the risk-neutral measure, and assumptions about r, t, and interest deductibility continue to hold.
Each GO requires an investment at date T of 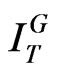 and provides stochastic EBIT of
and provides stochastic EBIT of  with an initial value of
with an initial value of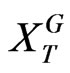 . The number of GOs available to the firm at date T,
. The number of GOs available to the firm at date T, 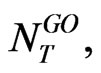 is an increasing linear function of the date T level of EBIT of the initial assets-in-place,
is an increasing linear function of the date T level of EBIT of the initial assets-in-place, :
:
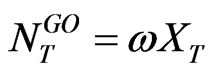 , (3.1)
, (3.1)
where 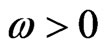 determines the extent of the firm’s growth potential. While the relationship specified in (3.1) is restrictive, it is also reasonable as it suggests that the number of growth options depends on the success of the technology used in assets-in-place [16].
determines the extent of the firm’s growth potential. While the relationship specified in (3.1) is restrictive, it is also reasonable as it suggests that the number of growth options depends on the success of the technology used in assets-in-place [16].
In bankruptcy shareholders receive nothing and bondholders receive the firm’s assets net of bankruptcy costs. Bankruptcy costs include the loss of the interest tax shield, the fraction a of assets-in-place, and the value of all GOs.
3.2. Modeling
We now we address the valuation and financing of a growth firm. As noted earlier, debt is inherently problematic because it causes management to underinvest in growth options [13]. A well-known means of mitigating the deadweight costs of underinvestment is to shorten debt maturity [7,13,20-24]. Thus, the growth firm in our model initially issues short-term debt that matures at date T, with coupon and principal denoted as CS and PS, respectively, and will issue perpetual debt immediately thereafter apropos its post-investment cash cow status. However, while this stage-wise debt policy mitigates the underinvestment problem, the problem remains potentially important. This is because, in some date T states where XT, and thus  are low, the value of the firm, denoted as
are low, the value of the firm, denoted as 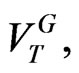 will be less than the principal payment due on maturing debt (i.e.,
will be less than the principal payment due on maturing debt (i.e.,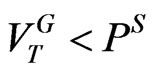 ), so the firm will declare bankruptcy and forgo GOs.
), so the firm will declare bankruptcy and forgo GOs.
Management chooses the amount of initial debt, measured by PS, that maximizes date 0 firm value, denoted as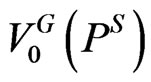 . In choosing PS, the tradeoff involves the tax benefits of the short-term debt through date T versus bankruptcy costs that are exacerbated by the loss of GOs. Since tax benefits are fixed (i.e., t is fixed), optimal leverage will be lower for a growth firm than an otherwise comparable cash cow because the former faces greater overall bankruptcy costs. The key question is: To what extent will GOs reduce optimal initial leverage?
. In choosing PS, the tradeoff involves the tax benefits of the short-term debt through date T versus bankruptcy costs that are exacerbated by the loss of GOs. Since tax benefits are fixed (i.e., t is fixed), optimal leverage will be lower for a growth firm than an otherwise comparable cash cow because the former faces greater overall bankruptcy costs. The key question is: To what extent will GOs reduce optimal initial leverage?
To value the growth firm, we begin by approximating the stochastic process for pre-investment EBIT, Xt, using a discrete binomial lattice through date T [25,26]. Initially ignoring default on the debt maturing at date T, each resulting binomial node value of XT determines the date T initial value of the pre-tax cash flow process for the firm in its post-investment cash cow state, 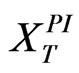 , which is the sum of XT and the initial EBIT provided by all exercised GOs,
, which is the sum of XT and the initial EBIT provided by all exercised GOs,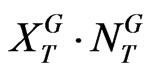 . The date T post-investment value of the growth firm at each node, denoted as
. The date T post-investment value of the growth firm at each node, denoted as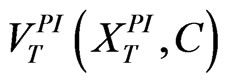 , is then calculated using the cash cow model (2.4), with optimal leverage. At each date T node, if
, is then calculated using the cash cow model (2.4), with optimal leverage. At each date T node, if  the firm will payoff the initial debt, whereas if
the firm will payoff the initial debt, whereas if  the firm will be bankrupt and creditors will receive
the firm will be bankrupt and creditors will receive 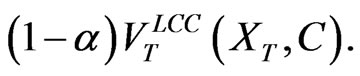 Given PS and values of the firm at all date T nodes, we can determine the time 0 value of the growth firm,
Given PS and values of the firm at all date T nodes, we can determine the time 0 value of the growth firm, 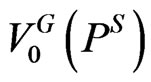 , by working recursively through the binomial lattice. Finally, optimal initial leverage for the growth firm is determined by finding the value of PS that maximizes
, by working recursively through the binomial lattice. Finally, optimal initial leverage for the growth firm is determined by finding the value of PS that maximizes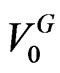 .
.
3.3. Numerical Estimates
To obtain base-case numerical estimates for growth firms, we use the same values for the basic parameters as we used for cash cows (μ = 0; ;
;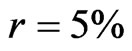 ;
;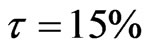 ; and
; and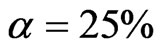 ). The initial value of assets-in-place is again
). The initial value of assets-in-place is again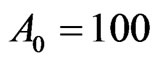 , and the base value of initial pre-tax cash flow again is
, and the base value of initial pre-tax cash flow again is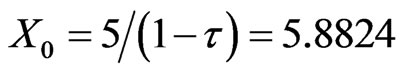 . Thus, Q values for growth firms are directly comparable to the null value of
. Thus, Q values for growth firms are directly comparable to the null value of 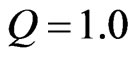 for a cash cow with no leverage and no agency costs, as well as cash cows with agency costs, as shown in Figure 1. Each GO provides EBIT of
for a cash cow with no leverage and no agency costs, as well as cash cows with agency costs, as shown in Figure 1. Each GO provides EBIT of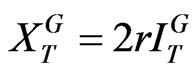 , and we vary w to analyze effects of growth-option intensity. Of course Q increases with w. For each value of w we determine the associated optimal (i.e., firm value-maximizing) leverage.
, and we vary w to analyze effects of growth-option intensity. Of course Q increases with w. For each value of w we determine the associated optimal (i.e., firm value-maximizing) leverage.
Results are displayed in Figure 2. The figure plots leverage against Q, rather than Q against leverage as in Figure 1, to be consistent with leverage regressions in aforementioned empirical studies, though actually the quantity of growth options (and more specifically, w) drives both Q and optimal leverage. We initially discuss the base-case results, which are shown with the solid curve. These results indicate a negative and highly convex relationship

Figure 2. Valuation and financing of growth firms.
between optimal leverage and Q. The left-most point on the curve is associated with a growth firm that has minimal growth options (i.e, is nearly a cash cow). For this firm 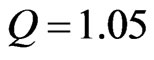 and optimal leverage is 50.4%. Thereafter optimal leverage falls steeply with Q, to 26.5% for a moderate-growth firm
and optimal leverage is 50.4%. Thereafter optimal leverage falls steeply with Q, to 26.5% for a moderate-growth firm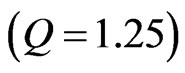 , to 11.9% for a highgrowth firm
, to 11.9% for a highgrowth firm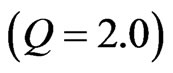 , and finally to 8.2% for a very high-growth firm
, and finally to 8.2% for a very high-growth firm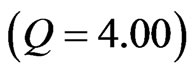 .
.
Thus, the base-case results are consistent with the arguments and evidence presented by Ogden and Wu [5]. As noted earlier, [5] find that the relationship between leverage and MB is negative and highly convex. The results are also consistent with Barclay et al. [16], who find that growth options have negative debt capacity.
Finally, we conduct sensitivity analysis of the effects of initial profitability. Varying from the base case where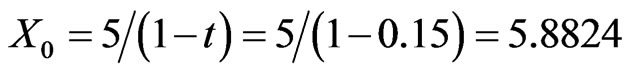 , we consider growth firms with: 1) low initial cash flow,
, we consider growth firms with: 1) low initial cash flow, 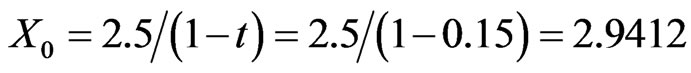 ; and 2) high initial cash flow,
; and 2) high initial cash flow, 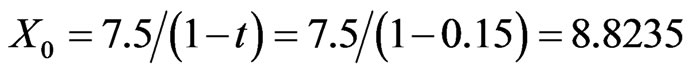 . For each initial cash flow level, we calculate Q and optimal leverage combinations for various values of growth option intensity, w. The resulting Q-leverage combinations are plotted in Figure 2. The dashed (dotted) line corresponds togrowth firms with low (high) initial cashflow.
. For each initial cash flow level, we calculate Q and optimal leverage combinations for various values of growth option intensity, w. The resulting Q-leverage combinations are plotted in Figure 2. The dashed (dotted) line corresponds togrowth firms with low (high) initial cashflow.
For both low and high initial cash flow firms, leverage bears a decreasing, convex relationship to Q. In addition, for each value of Q optimal leverage is lower (higher) than base-case optimal leverage for growth firms with low (high) initial cash flow. Thus, for growth firms the model estimates suggest a positive relationship between optimal leverage and profitability. As such, these results are inconsistent with the negative leverage-profitability relationship found empirically, though they are consistent with basic trade-off theory. Combined, the results shown in Figures 1 and 2 suggest that both leverage-Q and leverage-profitability relationships are potentially complex.
4. Summary
In this paper, we develop separate models for the valuation and financing of non-growth firms (cash cows) and growth firms because the two types of firms are prone to different agency problems; specifically, agency costs of managerial discretion apply for the former and agency costs of debt apply for the latter. Our models are “tradeoff” in nature because we incorporate not only the relevant agency costs but also tax benefits and bankruptcy costs associated with debt, and we use empirically relevant parameter values. For cash cows, model estimates indicate that these firms generally have relatively high leverage, though leverage, firm value, and profitability are all affected by variations in the efficacy of both internal and external governance mechanisms to control agency costs of managerial discretion. For growth firms: 1) optimal leverage is generally relatively low; 2) the relationship between optimal leverage and Tobin’s Q is negative and generally highly convex, and 3) optimal leverage increases with initial profitability. Model estimates for cash cows and growth firms suggest that both leverage-Q and leverage-profitability relationships are potentially complex. Many of our simulation results are consistent with empirical evidence, while other results provide suggestions for future empirical studies of leverageQ and leverage-profitability relationships.
REFERENCES
- F. Modigliani and M. Miller, “The Cost of Capital, Corporation Finance and the Theory of Investment,” American Economic Review, Vol. 48, 1958, pp. 267-297.
- A. Kraus and R. Litzenberger, “A State-Preference Model of Optimal Financial Leverage,” Journal of Finance, Vol. 28, No. 4, 1973, pp. 911-922. http://dx.doi.org/10.1111/j.1540-6261.1973.tb01415.x
- E. F. Fama and K. R. French, “Testing Trade-Off and Pecking Order Predictions about Dividends and Debt,” Review of Financial Studies, Vol. 15, No. 1, 2002, pp. 1- 33. http://dx.doi.org/10.1093/rfs/15.1.1
- M. Z. Frank and V. K. Goyal, “Capital Structure Decisions: Which Factors Are Reliably Important?” Financial Management, Vol. 38, No. 1, 2009, pp. 1-37. http://dx.doi.org/10.1111/j.1755-053X.2009.01026.x
- J. P. Ogden and S. Wu, “Reassessing the Effect of Growth Options on Leverage,” Journal of Corporate Finance, Vol. 23, 2013, pp. 182-195. http://dx.doi.org/10.1016/j.jcorpfin.2013.08.008
- J. Tobin, “A General Equilibrium Approach to Monetary Theory,” Journal of Money, Credit, & Banking, Vol. 1, No. 1, 1969, pp. 15-29. http://dx.doi.org/10.2307/1991374
- M. C. Jensen and W. H. Meckling, “Theory of the Firm: Managerial Behavior, Agency Costs and Ownership Structure,” Journal of Financial Economics, Vol. 3, No. 4, 1976, pp. 305-360. http://dx.doi.org/10.1016/0304-405X(76)90026-X
- M. C. Jensen, “Agency Costs of Free Cash Flow, Corporate Finance and Takeovers,” American Economic Review, Vol. 76, 1986, pp. 323-329.
- R. Stulz, “Managerial Discretion and Optimal Financing Policies,” Journal of Financial Economics, Vol. 26, No. 1, 1990, pp. 3-27. http://dx.doi.org/10.1016/0304-405X(90)90011-N
- S. F. Grossman and O. Hart, “Corporate Financial Structure and Managerial Incentives,” In: J. J. McCall, Ed., The Economics of Information and Uncertainty, University of Chicago Press, Chicago, 1982.
- J. Williams, “Perquisites, Risk, and Capital Structure,” Journal of Finance, Vol. 42, No. 1, 1987, pp. 29-49. http://dx.doi.org/10.1111/j.1540-6261.1987.tb02548.x
- J. Zwiebel, “Dynamic Capital Structure under Managerial Entrenchment,” American Economic Review, Vol. 86, 1996, pp. 1197-1215.
- S. C. Myers, “Determinants of Corporate Borrowing,” Journal of Financial Economics, Vol. 5, No. 2, 1977, 1977, pp. 147-175. http://dx.doi.org/10.1016/0304-405X(77)90015-0
- D. Hackbarth and D. C. Mauer, “Optimal Priority Structure, Capital Structure, and Investment,” Review of Financial Studies, Vol. 25, No. 3, 2012, pp. 747-796. http://dx.doi.org/10.1093/rfs/hhr129
- E. Morellec, B. Nikolov and N. Schurhoff, “Corporate Governance and Capital Structure Dynamics,” Journal of Finance, Vol. 67, No. 3, 2012, pp. 803-848. http://dx.doi.org/10.1111/j.1540-6261.2012.01735.x
- M. J. Barclay, C. W. Smith Jr. and E. Morellec, “On the Debt Capacity of Growth Options,” Journal of Business, Vol. 79, No. 1, 2006, pp. 37-59. http://dx.doi.org/10.1086/497404
- A. Dixit, “The Art of Smooth Pasting,” Routledge, New York, 1993.
- A. Korteweg, “The Net Benefits to Leverage,” Journal of Finance, Vol. 65, No. 6, 2010, pp. 2137-2170. http://dx.doi.org/10.1111/j.1540-6261.2010.01612.x
- P. G. Berger, E. Ofek and D. L. Yermak, “Managerial Entrenchment and Capital Structure Decisions,” Journal of Finance, Vol. 52, No. 4, 1997, pp. 1411-1438. http://dx.doi.org/10.1111/j.1540-6261.1997.tb01115.x
- C. W. Smith and J. Warner, “On Financial Contracting: An Analysis of Bond Covenants,” Journal of Financial Economics, Vol. 7, No. 2, 1979, pp. 117-161. http://dx.doi.org/10.1016/0304-405X(79)90011-4
- M. J. Barclay and C. W. Smith Jr., “The Maturity Structure of Corporate Debt,” Journal of Finance, Vol. 50, No. 2, 1995, pp. 609-631. http://dx.doi.org/10.1111/j.1540-6261.1995.tb04797.x
- M. J. Barclay, L. M., Marx and C. W. Smith Jr., “The Joint Determination of Leverage and Maturity,” Journal of Corporate Finance, Vol. 9, No. 2, 2003, pp. 149-167. http://dx.doi.org/10.1016/S0929-1199(02)00003-2
- S. A. Johnson, “Debt Maturity and the Effects of Growth Opportunities and Liquidity Risk on Leverage,” Review of Financial Studies, Vol. 16, No. 1, 2003, pp. 209-236. http://dx.doi.org/10.1093/rfs/16.1.209
- H. Leland and K. B. Toft, “Optimal Capital Structure, Endogenous Bankruptcy, and the Term Structure of Credit Spreads,” Journal of Finance, Vol. 51, No. 3, 1996, pp. 987-1019. http://dx.doi.org/10.1111/j.1540-6261.1996.tb02714.x
- J. Cox, S. Ross and M. Rubinstein, “Option Pricing: A Simplified Approach,” Journal of Financial Economics, Vol. 7, No. 3, 1979, pp. 229-263. http://dx.doi.org/10.1016/0304-405X(79)90015-1
- H. Wang, “Managerial Entrenchment, Equity Payout and Capital Structure,” Journal of Banking & Finance, Vo. 35, No. 1, 2011, pp. 36-50. http://dx.doi.org/10.1016/j.jbankfin.2010.07.018
NOTES
*Corresponding author.

