ABSTRACT

In this paper, we prove the celebrated Bichteler-Dellaccherie Theorem which states that the class of stochastic processes X allowing for a useful integration theory consists precisely of those processes which can be written in the form X = X₀ + M + A, where M₀ = A₀ = 0, M is a local martingale, and A is of finite variation process. We obtain this decomposition rather direct form an elementary discrete-time Doob-Meyer decomposition. By moving to convex combination we obtain a direct continuous time decomposition, which then yield the desired decomposition. We also obtain a characterization of semi-martingales in terms of a variant no free lunch with vanishing risk.

1. Introduction

In this paper, is assumed to be a filtered probability space where is a filtration satisfying for all, the usual condition of right continuity and completeness. The random movement of risky assets in the market is modeled via cadlag, nonnegative stochastic processes, where. We assume that all wealth processes are discounted by another special asset which is considered a baseline. In the market described above, economic agents can trade in order to reallocate their wealth.

Consider a simple predictable process

.

where, and for all, is a finite stopping time and is -measurable.

Each, , is an instance when some give economic agent may trade in the market, then, is the number of unit from the ith risky assets that the agent will hold in the trading interval. This form of trading is called simple, as it comprises of finite number of buy-and-hold strategies, in contrast to continuous trading where one is able to change the position of the assets in a continuous fashion. The last form of trading is only theoretical value, since it cannot be implemented in reality, even if one ignores market frictions.

Starting from initial capital and following the strategy described by the simple predictable process

, the agent’s discounted process is given by

.

where, are a.s. finite stoping times with respect to and the are -measurable real random variables. Note that the trader is allowed to trade on an infinite time horizon, because we do not restrict to bounded stoping times for the re-allocation of the capital. Of course trading on a finite time horizon [0, T] is covered by switching to the process.

Theorem 1.1. [1,2] A real valued, cadlag, adapted process the following are equivalent:

1) X is a good integrator.

2) X may be decomposed as, where is a local martingale and is an adapted process of finite variation.

Defination 1.1. [1,3] A real valued, cadlag, adapted process allows for A Free Lunch With Vanishing Risk for simple integrands if there is a sequence of simple integrands such that for,

.

and

In contrast, X therefore admits No Free Lunch With Vanishing Risk (NFLVR) for simple integrands if for every sequence satisfying (VR) we have

(NFL)     in probability.

A free lunch with vanishing risk (FLVR) for simple integrands indicates that S allows for a sequence of trading schemes, each involving only finitely many rebalancing of the portfolio, such that the losses tend to Zero in the sense that of (VR) ,while the terminal gains (FL) remain substantial as n goes to infinity. It is important to note that the condition (VR) of vanishing risk pertains the maximal losses of the trading strategy during the entire interval [0,T]: if the left hand side of (VR) equals this implies that, with probability one, the strategy never, i.e. for not, cause an accumulated loss of more than.

Resently, it has been argued that existence of an Equivalent Martingale Measure(EMM) is not necessary for viability of the market; to see this effect, see [4-6]. In [7], the concept of strictly positive supermartingale deflator which is weaker than the existence of an EMM, that allows for consistent theory to be developed.In this paper, we investigate the relation between the no free lunch with vanishing risk property for simple integands and the semimartingale property.

Theorem 1.2. [1,8] Let be a real-valued, cadlag, locally bounded process based on and adepted to a filtered probability space. If S satisfies the condition of no free lunch with vanishing risk (NFLVR) for simple integrands then S is a semimartingale.

Theorem 1.3. For a locally bounded, adopted, cadlag process X the following are equivalent 1) X satisfies NFLVR + LI(little Investment)

2) X is a classical semimartingale.

Theorem 1.4. For an adapted cadlag process X the following are equivalent.

1) For all sequences of simple predictable processesa)

b)

together imply in probability.

2) X is a classical semimartingale.

Proposition 1.5. Let be cadlag and adapted, with X₀ and such that and X satisfies NFLVR + LI For all there is and a sequence of stopping times such that, for all n 1) takes values in.

2).

3) The stopped processes and satisfyfor all n, and

Lemma 1.6. Under the assumptions as in the proposition above with

the sequence is bounded in probability.

Proof. For all n, let

a simple predictable process, then since

since X satisfies NFLVR + LI, is bounded in.

For define a sequence of stopping times

.

Given there is such that

Lemma 1.7. Under the same assumptions as in Proposition 1.5 the stopped martingales satisfy

.

Proof. For and, since the are predictable and the are martingales,

we write as a telescoping series and simplifying to get

Lemma 1.8. Let

.

Under the assumption of Proposition 1.5 the sequence is bounded in probability.

Proof. Assume for contradiction that is not bounded in probability. Then there is such that for all k there is such that For define

and

.

Then and

and at time t = 1 we have

.

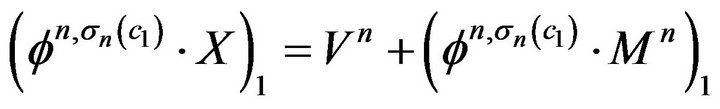  But the second summand is bounded in L², so we conclude that is not bounded in probability.

We defined a sequence of stopping times

.

Because

by Doob’s sub-martingale in-equality,(see [9,10])

is bounded in probability. Therefore there is such that. Note that is uniformly bounded below by. We claim is not bounded in probability. Indeed, for any n and any k,

Since, the probability of the other event is at least. This gives the desired contradiction because it is now easy to construct a FLVR + LI.

Proof of Proposition 1.5: Defined a sequence of stopping times

.

By Lemma 1.8 there is c₂ such that. Take and

Lemma 1.9. [11]. Let be measurable functions, where f is left continuous and takes finitely many values. Say. Define

where is the biggest of the k such that X_k less than or equal to t. Then for all partition,

Proposition 2.0. Let be cadlag and adopted, with and such that and X satisfies NFLVR + LI. For all there is C and a valued stopping time such that

and sequence and of continuous time cadlag processes such that for all n1)

2)

3) is a martingale with

4)

Proof. Let be given. Let C, , , and be as in proposition 1.5. Extended and to all by defining and

. Not that the extended is no longer predictable, and currently we only have control of the total variation of over, i.e.

Notice that, for,

From this and it follow that

, so. How do we fine the limit of the sequence of stopping times? The trick is to define, a simple predicator process, and note that stopping at is like integrating R_n, i.e. and. We have that

.

Apply Komlos’ Lemma to obtain convex weights such that

a.s as By the dominated convergence theorem,. Observe that

Define. Each is left continuous, decreasing process. In particular, , so we can divide by this quantity. We claim that . In deed, on the event, so

Define new processes. Then and. Thus we define Mⁿ and Aⁿ by

The total variation of over is bounded by 3. By Lemma 1.9,

That follows from the fact that

. To finish the proof, we show that there is a subsequence such that satisfies. We know because. Since a.s there is a subsequence such that. Finally,

Therefore, and have the desired properties.

Proof of the Main Theorems Proof of Theorem 1.3. We may assume the hypothesis of proposition. Let and take C, , , as in proposition. Apply komlos lemma to find convex weights such that

for all, where the convergence is a.s. For all n,

so the total variation of A over D is bounded by C. Further, we have. A is a cadlag on D, so define it on all of [0,1] to make it cadlag. M is martingale so it has a cadlag modification. Since and was arbitrary, and the class of classical semimartingales is local, X must be a classical semimartingale.

Proof of Theorem 1.4. We no longer assume that X is locally bounded. The trick is to leverage the result for locally bounded processes by subtracting the big jump from X. Assume without loss of generality that and defined. Then X = X − J is an adopted, cadlag locally bounded process. We will show that theorem 1.4 for X implies NFLVR + LI for X, so that we may apply theorem 1.3 to X. Then since J is finite variation, this will then imply X is a classical semimartingale .

Suppose are such that and. We need to prove that in probability . First we will show that.

by the assumptions on

By (1), in probability. Since

in probability, we conclude that

in probability. Therefore X satisfies NFLVR + LI.

REFERENCES

NOTES

^*Supported by the NNSF of China (11171001), HSSPF of the Ministry of Education of China (10YJA910005), Talents youth Fund of Anhui Province Universities (2010SQRL016ZD), Academic Innovation Team of Anhui University (KJTD001B) and Youth Science Research Fund of Anhui University (2009QN011A).