Journal of Mathematical Finance
Vol.3 No.1(2013), Article ID:28120,9 pages DOI:10.4236/jmf.2013.31001
Market Microstructure and Price Discovery
1Centre of Mathematics for Applications, Department of Mathematics, University of Oslo, Oslo, Norway
2Department of Functional Analysis, Mechanical and Mathematical Faculty, Belarusian State University, Minsk, Belarus
Email: paulck@math.uio.no, yablonski@bsu.by, proske@math.uio.no
Received July 13, 2012; revised September 18, 2012; accepted October 4, 2012
Keywords: Price Theory and Market Microstructure; Stochastic Difference Equations; Bid; Ask; Price Processes in Discrete Time
ABSTRACT
The design of this study is to investigate the evolution of a stochastic price process consequent to discrete processes of bids and offers in a market microstructure setting. Under a set of flexible assumptions about agent preferences, we generate a price process to compare with observation. Specifically, we allow for both rational and irrational economic behavior, abstracting the inquiry from classical studies relying on utility theory. The goal is to provide a set of economic primitives which point inexorably to the price processes we see, rather than to assume such process from the start.
1. Introduction
We propose to model a price process based on microstructural activity of a market. We assume a set of agents such that each agent at any moment has both bid and ask prices present in the market. A trade occurs if and only if the bid of one agent is equal to the ask of another, this common value becoming the price of a trade. We calculate the dynamics of the resulting price process, including the moments of trades, in a discrete time setting for behavioral choices of the agents. These choices are formalized in relevant probability distributions specific to the agents’ behaviors. In this way, we allow for a multitude of behavioral patterns, including, but not restricted to traditional motivations inspired by utility functions. Our model is flexible enough to allow for “marks” to a trade, ancillary data such as its time stamp, so that we may study independently such features as trade clustering and time deformation.
Recent history is rich with microstructure studies of financial markets and with associations of specific families of probability distributions to financial stochastic processes. For good reviews of the microstructure literature see these works respectively [1,2]. For associations of probability distributions such as the widely applied Gaussian, normal inverse Gaussian, and more inclusively the generalized hyperbolic, see these studies [3,4]. In many instances such inquiries assume at the outset various forms of stochastic processes, as defined by stochastic differential equations, and then set forth to estimate parameters. Popular choices are Itô diffusions and Ornstein-Uhlenbeck processes, with and without the superposition of pure jump Lévy processes.
Most studies of microstructure take an econometric approach, that is, they define some structure, assume distributions as appropriate, then estimate parameters using data. In his survey with important bibliography, Bollerslev reviews the state of financial econometrics [5]. In a subsection discussing time-varying volatility, he notes that, “several challenging questions related to the proper modeling of ultra high-frequency data, longer-run dependencies, and large dimensional systems remain.” Further in the text, he qualifies this remark by stating: “Not withstanding much recent progress, the formulation of a workable dynamic time series model which readily accommodates all of the high-frequency data features, yet survives under temporal aggregation, remains elusive.”
Engle provides just such an econometric study [6] employing the Autoregressive Conditional Duration (ACD) model developed by him with Russell [7] in the study of IBM stock transactional arrival times. In the former paper, Engle, in referring to cases of the conditional duration function, relates, “In each case, the density is assumed to be exponential.” Such assumptions are typical, and necessary, for an econometric study focusing on time series of prices as the fundamental data structure.
Hasbrouck, in focusing on the refinement of bid and ask quotes, proposes and estimates an Autoregressive Conditional Heteroskedasticity (ARCH) model using Alcoa stock transactions, evenly spaced at 15 minute intervals [8]. Routinely, he asks the reader to consider, “a stock with an annual log return standard deviation of 0.30” The reference “return” is of course to the price sequence, a necessary expedient in the classical econometric framework which considers a price process as fundamental, rather than consequential to a set of underlying bid and ask processes.
Other studies, such as one by Bondarenko, delve into the bid and ask series, but rather as a difference, the spread [9]. The focus of this work and its principal results are in the realm of market liquidity, rather than in the estimation of the price process. Once again, the classical framework requires an assumption on the distribution of the price process, as evidenced in this remark made within the context of evaluating a price change between periods. “The asset’s final value is denoted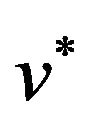 , a normal random variable with mean
, a normal random variable with mean 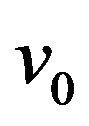 and variance
and variance .”
.”
Yet further studies attempt to develop directly a price process from first principles. An interesting and provocative example is a paper by Schaden, which formulates conclusions from financial analogues to fundamentals of quantum physics [10]. As he observes in the introduction, “At this stage it is impossible to decide whether a quantum description of finance is fundamentally more appropriate than a stochastic one, but quantum theory may well provide a simpler and more effective means of capturing some of the observed correlations.” Indeed, though the basic process investigated is yet a price process, not those of bids and asks. The analysis is grounded on five at first qualitative assumptions about the market, and concludes with the assertion that the evolution of prices follows “the lognormal price distribution.” In this setting it is difficult to discern how a different—and more realistic—distribution could emerge without changing substantially the assumptions, or the physics. For further background reading see [11-13].
In our paper we choose to move to a more basic level of explanation, to specify the market mechanisms among interacting agents, and then to let the model determine the price process and its features. In this way we derive such features as the distributions of prices, rather than assuming them ab initio.
We now proceed forthwith to present our case.
2. Specification of the Model
We consider for simplicity the model of the market for one stock in discrete time 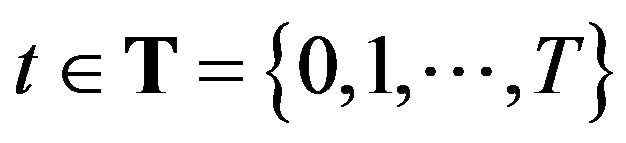 1. It is reasonable to assume that in each time
1. It is reasonable to assume that in each time 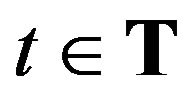 there are only finite number
there are only finite number  of agents taking part in the trading on the market. Let
of agents taking part in the trading on the market. Let  be the number of all agents which have ever taken part in trading. At each moment
be the number of all agents which have ever taken part in trading. At each moment  the agent number i,
the agent number i, 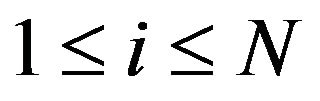 proposes a bid price
proposes a bid price 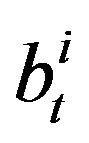 and an ask price
and an ask price 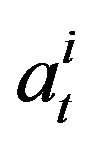 for a goods on the market. We assume that
for a goods on the market. We assume that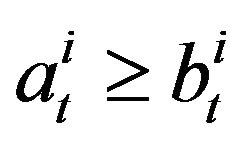 . It is convenient to set
. It is convenient to set 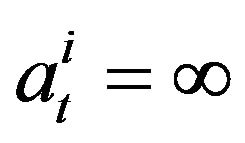 and
and 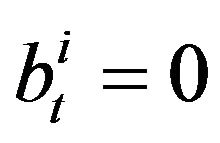 if at the moment
if at the moment 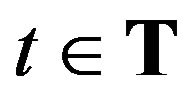 the
the 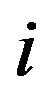 -th agent does not take part in the trading. Supposing the rational behavior of agents on the market we have
-th agent does not take part in the trading. Supposing the rational behavior of agents on the market we have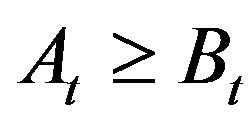 , where
, where 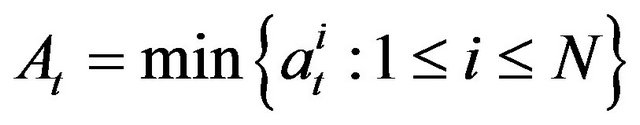 and
and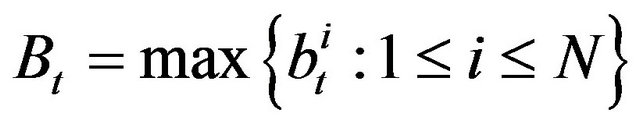 . We say that there is a trade between
. We say that there is a trade between  -th and
-th and  -th agents at moment
-th agents at moment 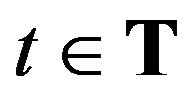 if
if 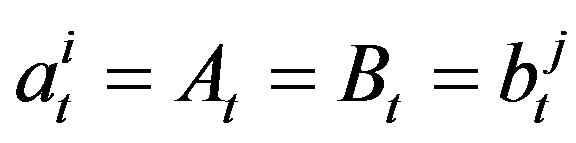 or
or 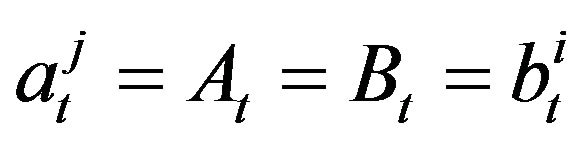 . It means that there is a trade between agents with minimal ask price
. It means that there is a trade between agents with minimal ask price 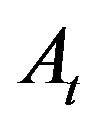 and maximal bid price
and maximal bid price 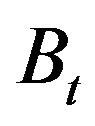 provided that they are equal
provided that they are equal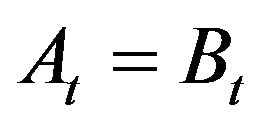 . In order to escape some pathological examples we always assume that at every time t there exist two different agents, say number i and j, i ≠ j, such that
. In order to escape some pathological examples we always assume that at every time t there exist two different agents, say number i and j, i ≠ j, such that 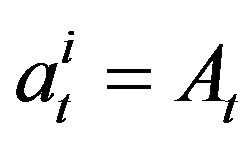 and
and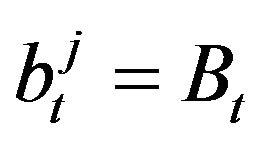 . In the case when more than one of the agents have the same minimal ask price and maximal bid price, say
. In the case when more than one of the agents have the same minimal ask price and maximal bid price, say 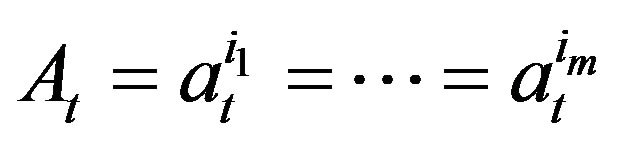 and
and , we suppose that a trade occurs between agents with numbers
, we suppose that a trade occurs between agents with numbers 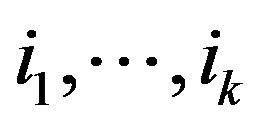 and
and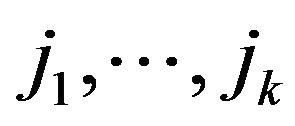 , where
, where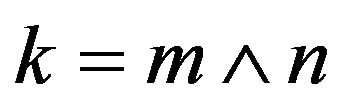 .
.
The bids and asks can be changed only by the agents. It may happen that 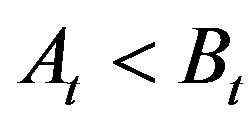 after such changing of prices. In order to avoid such possibilities we suppose that bid prices can be changed by agents only at even moments and ask prices only at odd moments. Nevertheless the trades can occur at any moment: even or odd.
after such changing of prices. In order to avoid such possibilities we suppose that bid prices can be changed by agents only at even moments and ask prices only at odd moments. Nevertheless the trades can occur at any moment: even or odd.
How should the bid and ask prices change? The rules of changing bid and ask prices by the agents are different for each agent and they are based on different reasons; for instance: aims of agents, interpretations of information, personal reasons, and so on. If these prices are changed at time  when a trade occurs, say between the i-th and j-th agents with prices
when a trade occurs, say between the i-th and j-th agents with prices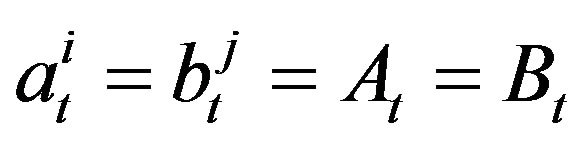 , then the respective ask price
, then the respective ask price 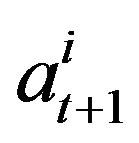 will be not less then the price before the trade
will be not less then the price before the trade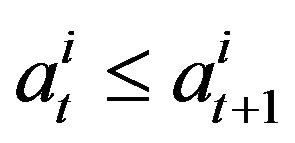 . Therefore we can say that
. Therefore we can say that
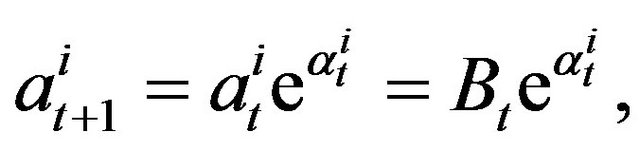
where  is a nonnegative random variable (it is possible to add one more value
is a nonnegative random variable (it is possible to add one more value  if the agent decides to leave the market). For the bid prices we can write similarly
if the agent decides to leave the market). For the bid prices we can write similarly

with nonnegative random variable 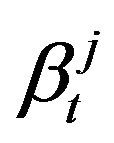 (with the same note about
(with the same note about ). The random variables
). The random variables  and
and  are
are 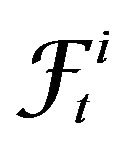 - and
- and  -adapted, respectively, where
-adapted, respectively, where 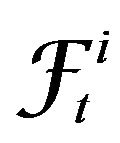 and
and  are
are  -fields containing information which the agents know before the time
-fields containing information which the agents know before the time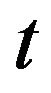 , inclusively. Note that
, inclusively. Note that 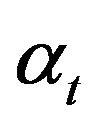 and
and 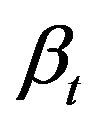 are defined only at the moment
are defined only at the moment 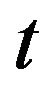 of trades.
of trades.
As in the previous case we can write the same equalities for a moment 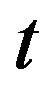 when the respective agent was not involved in a trade. Hence for any
when the respective agent was not involved in a trade. Hence for any 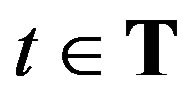 we have
we have
 (2.1)
(2.1)
where 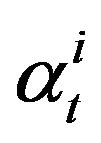 and
and ,
, 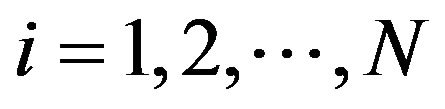 are nonnegative random variables. The moment
are nonnegative random variables. The moment 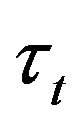 and the price
and the price 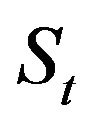 of the last trade before time
of the last trade before time  inclusively are given by
inclusively are given by
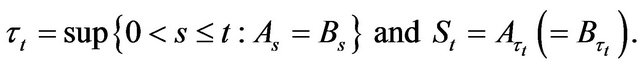 (2.2)
(2.2)
Set 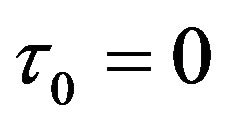 and
and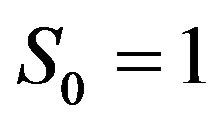 .
.
The purpose of present paper is to calculate the distributions of 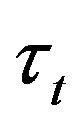 and
and  from Equation (2.2) by using the known distributions of
from Equation (2.2) by using the known distributions of 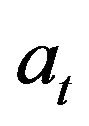 and
and 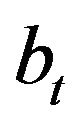 from Equations (2.1).
from Equations (2.1).
Taking min and max in Equations (2.1) yields
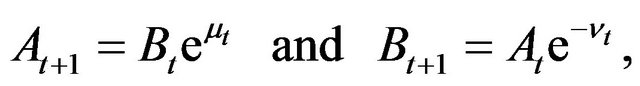 (2.3)
(2.3)
where  and
and
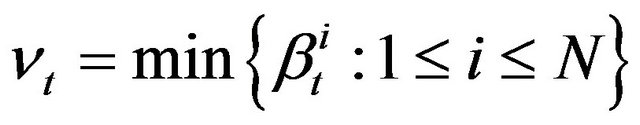 are nonnegative random variables. Notice that
are nonnegative random variables. Notice that 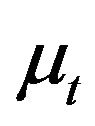 and
and 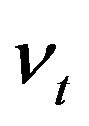 are
are 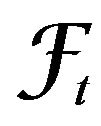 -measurable, where
-measurable, where 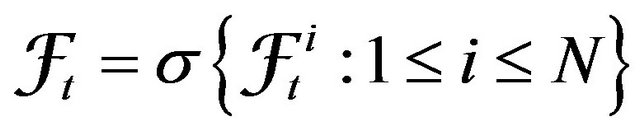 is information known to at least one agent before time
is information known to at least one agent before time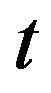 , inclusively.
, inclusively.
Let us consider two nonnegative random processes 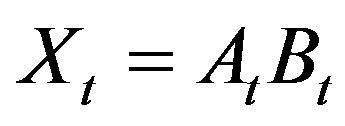 and
and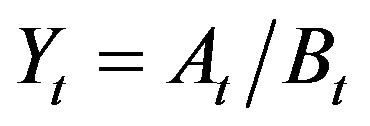 . From Equalities (2.3) we deduce that
. From Equalities (2.3) we deduce that
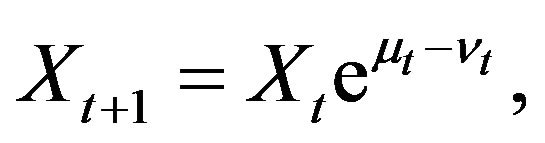 (2.4)
(2.4)
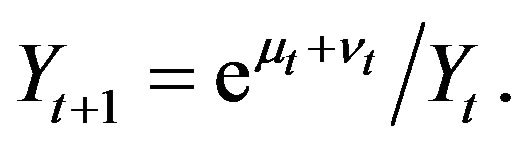 (2.5)
(2.5)
Since the trade occurs at the moment 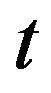 if and only if
if and only if 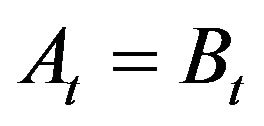 or, equivalently, if
or, equivalently, if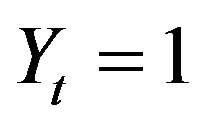 , then the last moment of a trade before the time
, then the last moment of a trade before the time 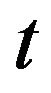
 (2.6)
(2.6)
is the last moment before 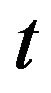 when the process
when the process 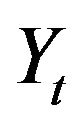 reached the level 1. The price of the last trade before the time
reached the level 1. The price of the last trade before the time 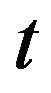 is given by
is given by
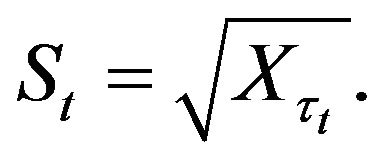 (2.7)
(2.7)
Now the problem is reduced to finding the law of random time 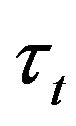 given by (2.6) and the law of the process
given by (2.6) and the law of the process 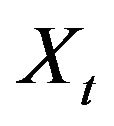 given by Equation (2.4) at the time
given by Equation (2.4) at the time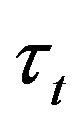 .
.
3. Simplest Behavior of Agents
Since the bid prices can be changed by the agent in even moments only, then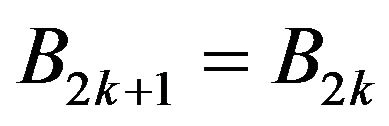 . Therefore from Equation (2.3) we deduce that
. Therefore from Equation (2.3) we deduce that
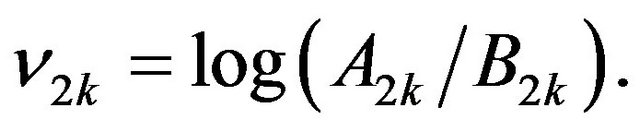 (3.1)
(3.1)
Similarly 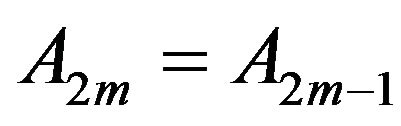 and
and
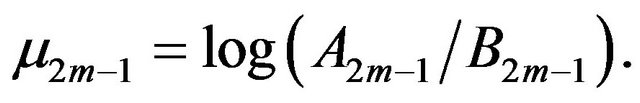 (3.2)
(3.2)
Then Equations (3.1), (3.2) and (2.5) imply that 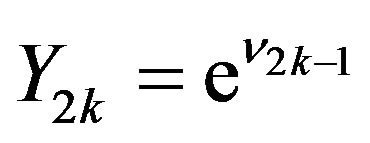 and
and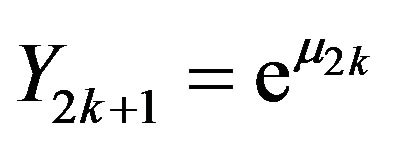 . Moreover, we have
. Moreover, we have  and
and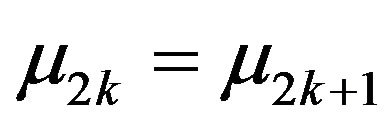 . Define a new sequence
. Define a new sequence 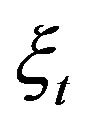 by
by 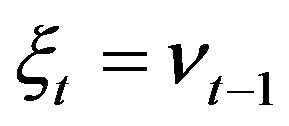 for
for 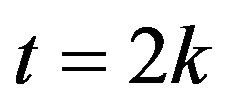 and
and 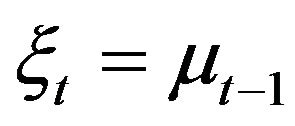 if
if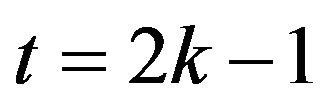 ,
, . Then
. Then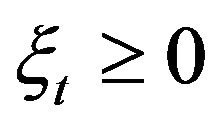 ,
, 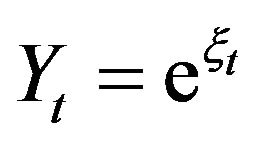 and
and 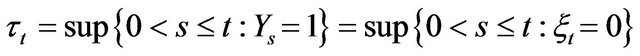 . Hence the trade occurs at time
. Hence the trade occurs at time  if and only if
if and only if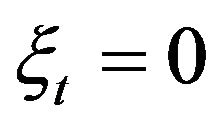 .
.
In order to obtain some result we need to have more assumptions on the behavior of the processes  and
and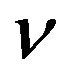 . The simplest assumption is that
. The simplest assumption is that ,
, 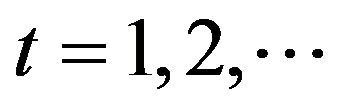 is a sequence of independent identically distributed (i.i.d.) random variables. Denote by p the probability that
is a sequence of independent identically distributed (i.i.d.) random variables. Denote by p the probability that 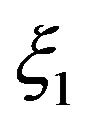 takes value zero:
takes value zero: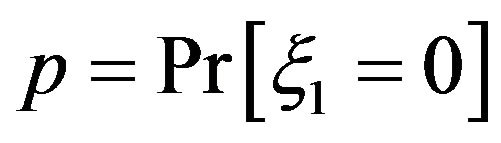 . The variable
. The variable 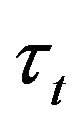 is a last zero of the sequence
is a last zero of the sequence  before the moment
before the moment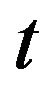 . We put
. We put 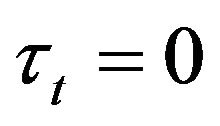 if there are no zeros (no trades) before time
if there are no zeros (no trades) before time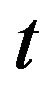 , inclusively. Hence
, inclusively. Hence 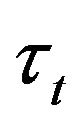 takes values
takes values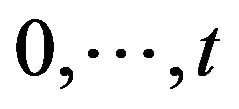 . The probabilities of these values are given by
. The probabilities of these values are given by
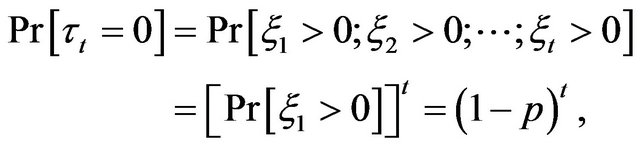
and for 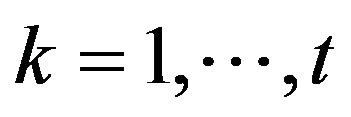
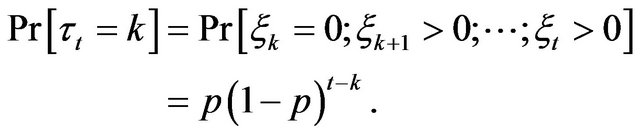
Let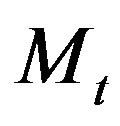 ,
, 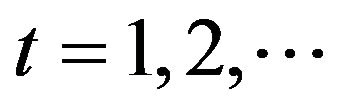 denote the number of trades before time t inclusively. Hence
denote the number of trades before time t inclusively. Hence 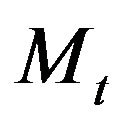 is number of zeros in the sequence
is number of zeros in the sequence ,
,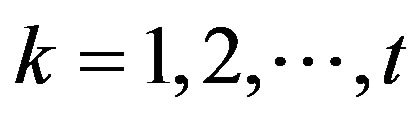 . Then
. Then 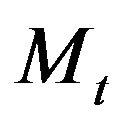 has a binomial distribution with parameters
has a binomial distribution with parameters 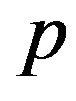 and
and , i.e.,
, i.e.,
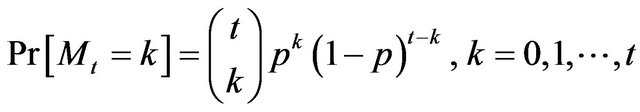
here 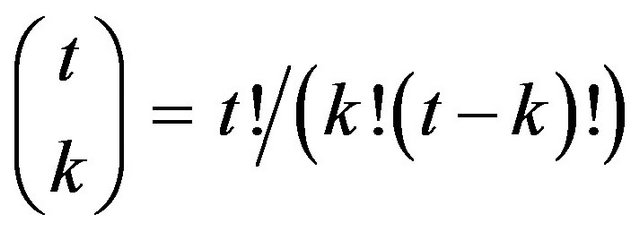 is a binomial coefficient.
is a binomial coefficient.
Moreover 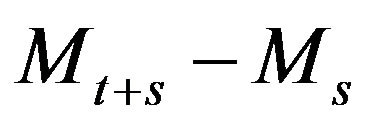 has a binomial distribution with the same parameters
has a binomial distribution with the same parameters 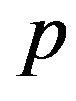 and
and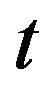 . As a consequence of independence of the variables
. As a consequence of independence of the variables 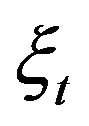 we get that for any
we get that for any 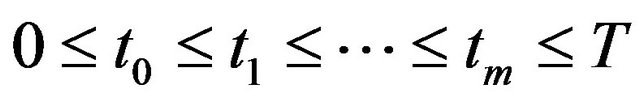 the random variables
the random variables 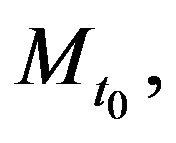
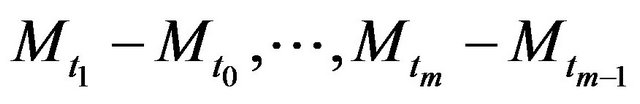 are independent.
are independent.
Define the sequence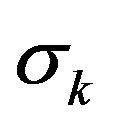 ,
, 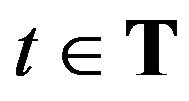 of random times inductively by the following expression.
of random times inductively by the following expression.
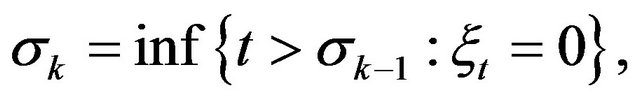
with  and
and . We adopt the convention that the infinum of empty set is equal to infinity. Then
. We adopt the convention that the infinum of empty set is equal to infinity. Then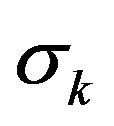 ,
, 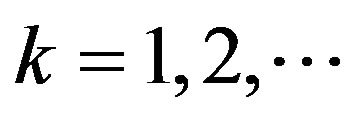 is a moment of
is a moment of 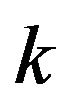 -th trade (or zero of the sequence
-th trade (or zero of the sequence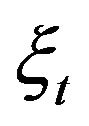 ) and
) and
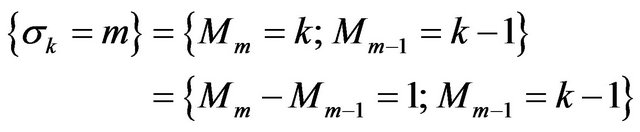
for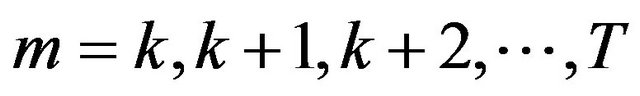 . Easy calculation shows that
. Easy calculation shows that
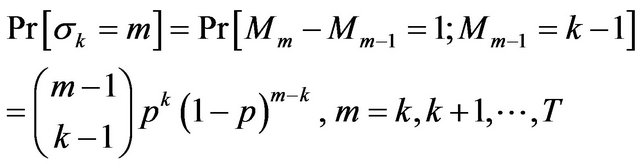
and
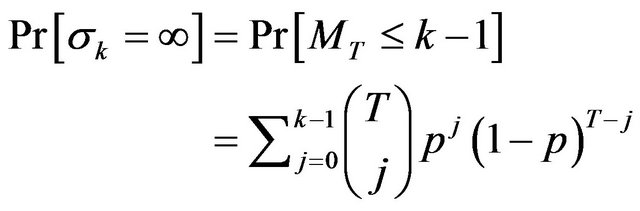 .
.
Furthermore for all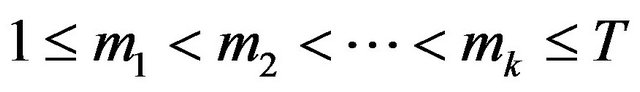 ,
, 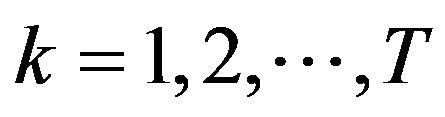 we have
we have

and
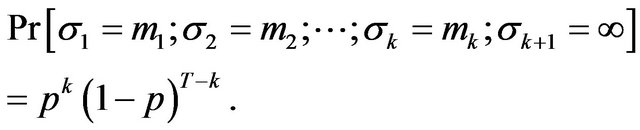
For any 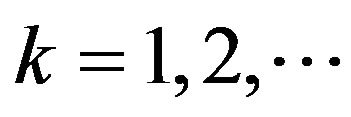 and
and 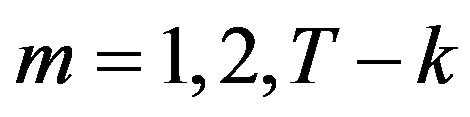 we have
we have

and
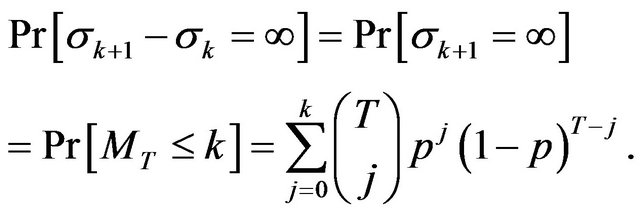
In the same way one can obtain
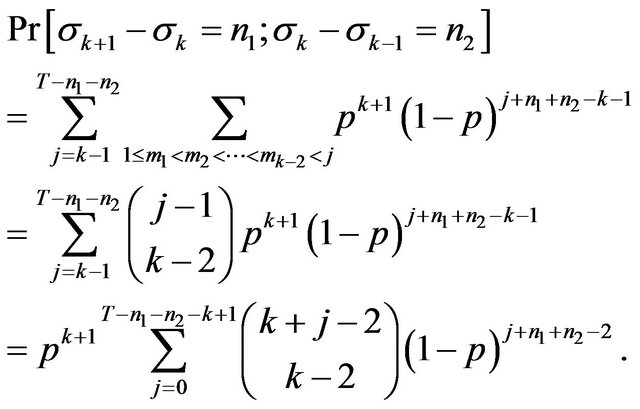
Notice that
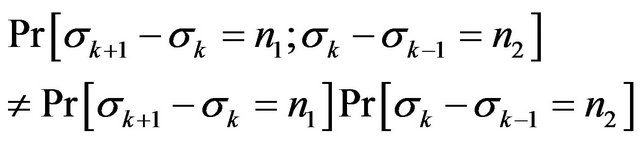 .
.
Hence 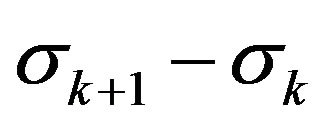 and
and 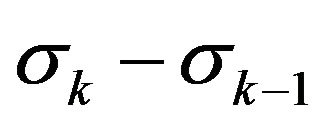 are not independent.
are not independent.
Let us consider process  given by Equation (2.4). The solution of this equation can be written as
given by Equation (2.4). The solution of this equation can be written as
 (3.3)
(3.3)
Since  and
and 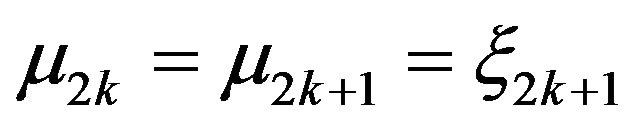 then
then

where 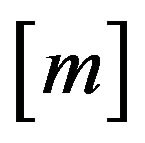 denotes the integer part of number
denotes the integer part of number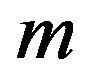 .
.
Therefore taking into account that 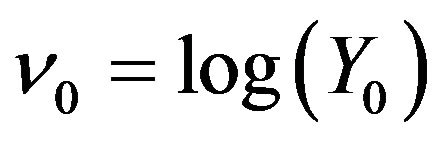 one has
one has
 (3.4)
(3.4)
From the Equation (3.4) and definition of 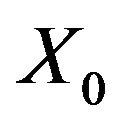 and
and 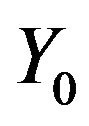 we obtain the prices
we obtain the prices 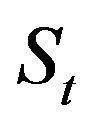 and
and 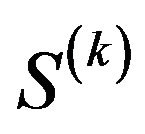 of the last trade and the
of the last trade and the 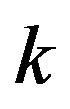 -th trade:
-th trade:
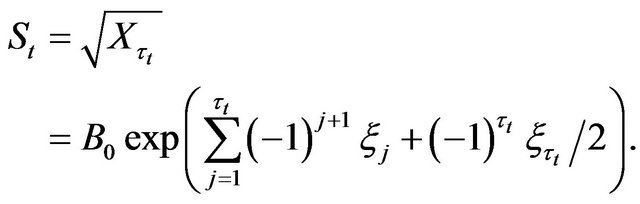 (3.5)
(3.5)
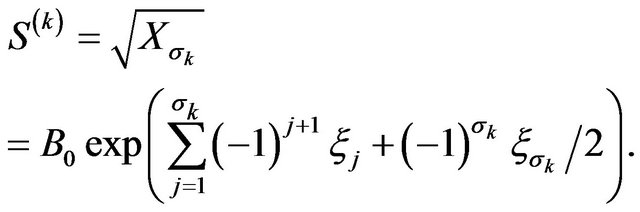 (3.6)
(3.6)
Now we calculate the characteristic function 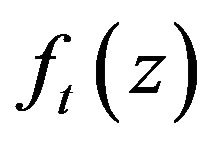 of the logarithm
of the logarithm . It follows from representation (3.5) that
. It follows from representation (3.5) that
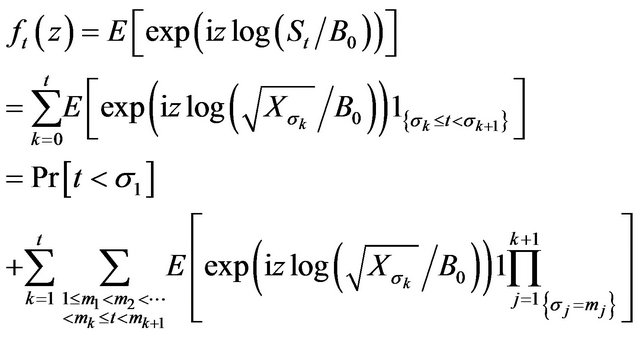
Notice that event 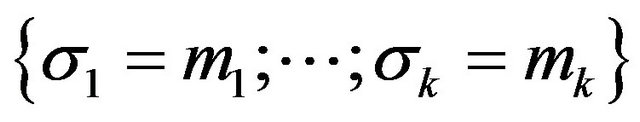 occur if and only if
occur if and only if 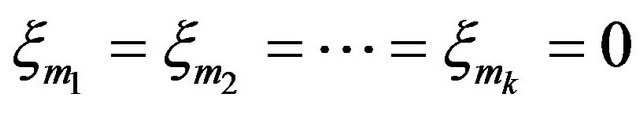 and
and 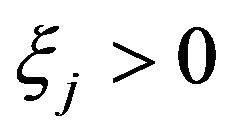 if
if  does not coincide with some of the
does not coincide with some of the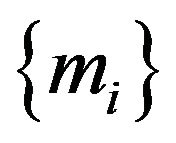 . This fact, formula (3.5), independence and the distribution of
. This fact, formula (3.5), independence and the distribution of 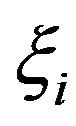 imply
imply

where 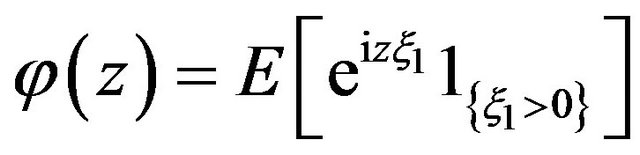 is the characteristic function of
is the characteristic function of 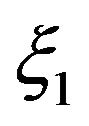 conditioned on
conditioned on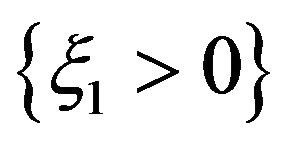 . From the relationships
. From the relationships 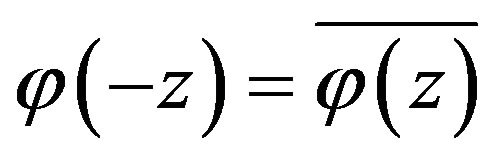 and
and 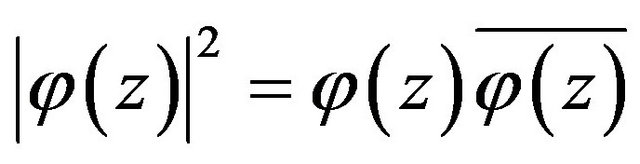 we have
we have
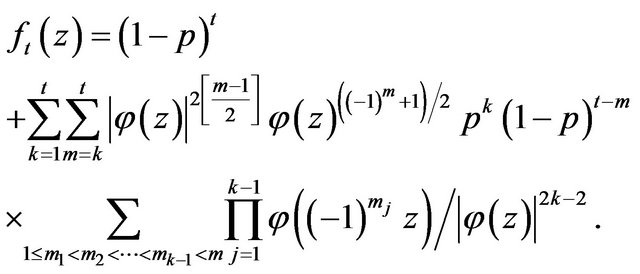 (3.7)
(3.7)
Notice that if only  numbers of
numbers of  are even then
are even then
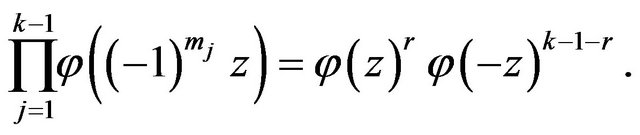
Therefore
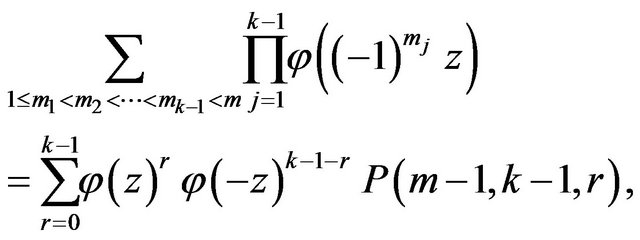
where 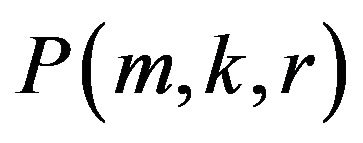 is a number of possibilities to choose
is a number of possibilities to choose 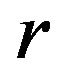 even and
even and  odd numbers from the set
odd numbers from the set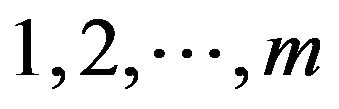 . Here
. Here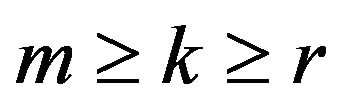 . There are only
. There are only 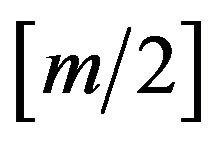 even and
even and 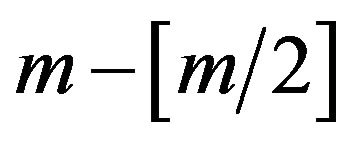 odd numbers among
odd numbers among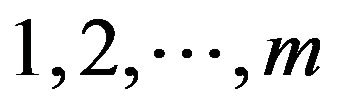 . Hence
. Hence
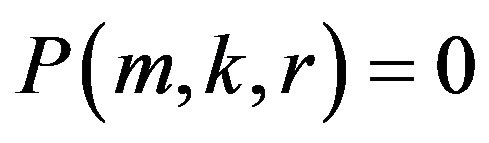 if
if 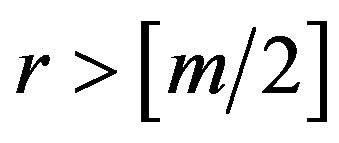 or
or 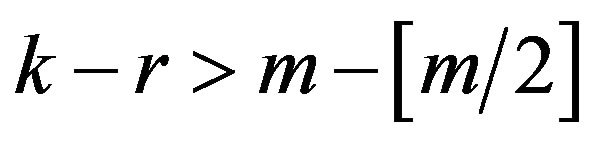 and
and
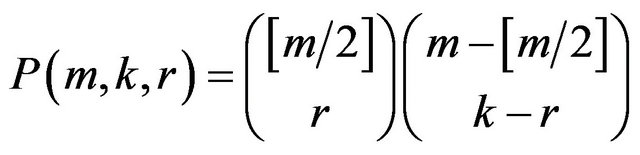 if
if 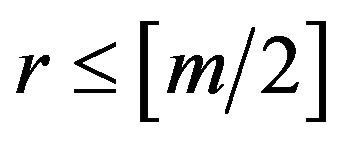 and
and
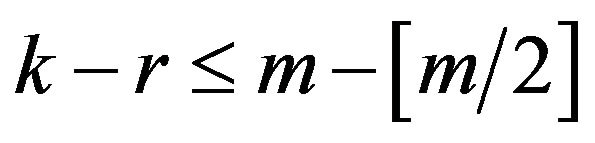 . Putting this expression into the Formula (3.7) yields
. Putting this expression into the Formula (3.7) yields

Using equation (3.6) one can compute joint characteristic function 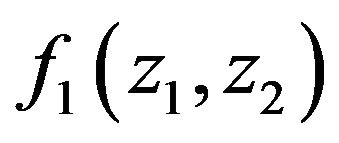 of the moment
of the moment 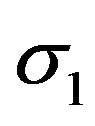 of the first trade and the logarithm
of the first trade and the logarithm 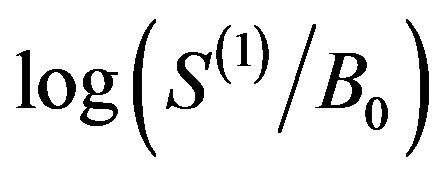 provided there was at least one trade,
provided there was at least one trade, 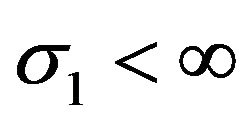 in the following way
in the following way
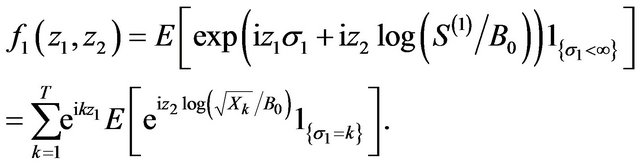
Since 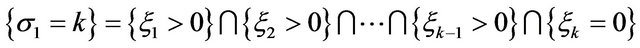 and the random variables
and the random variables 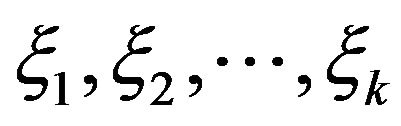 are independent then
are independent then
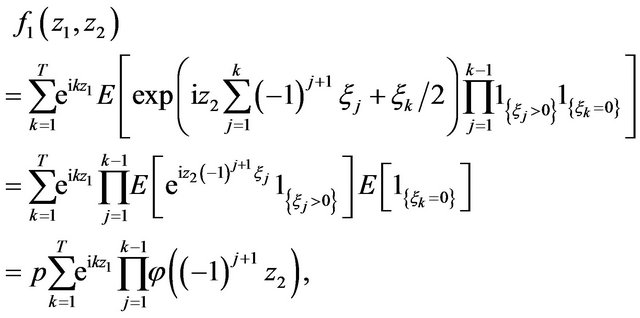
(3.8)
where 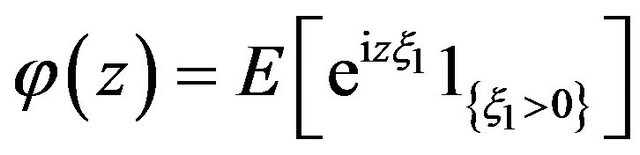 is defined above. The relationships
is defined above. The relationships  and
and  imply
imply
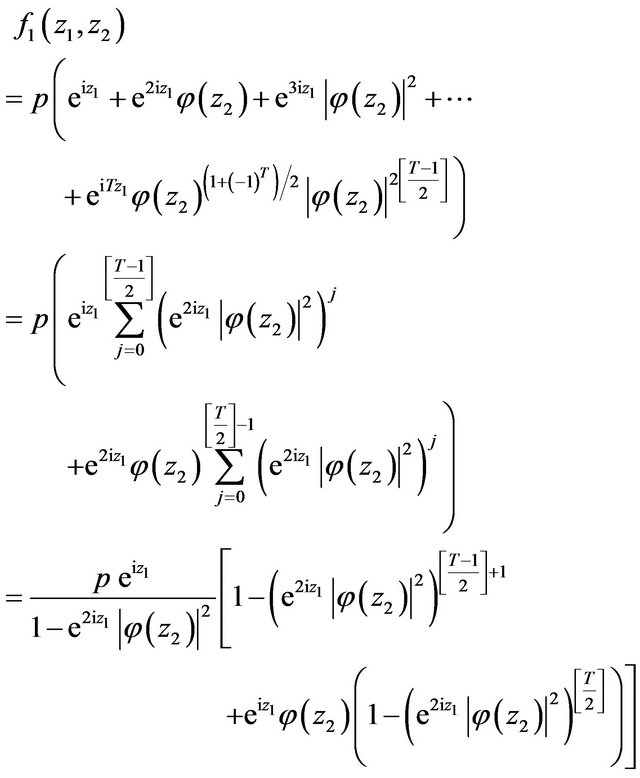
Similarly we can find joint characteristic function 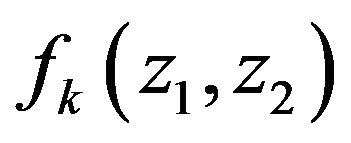 of the difference
of the difference 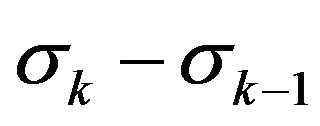 between moments of
between moments of 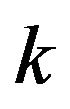 -th and
-th and 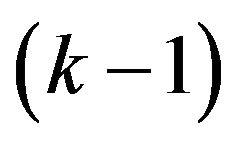 -st trades,
-st trades, 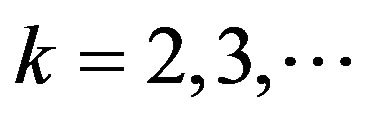 and the logarithm
and the logarithm  of the ratio between these trades provided there were at least
of the ratio between these trades provided there were at least 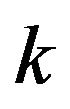 trades, ,
trades, ,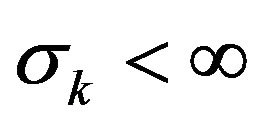 .
.

Since 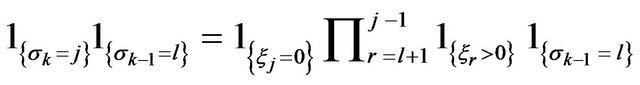 and all multipliers here are independent then
and all multipliers here are independent then
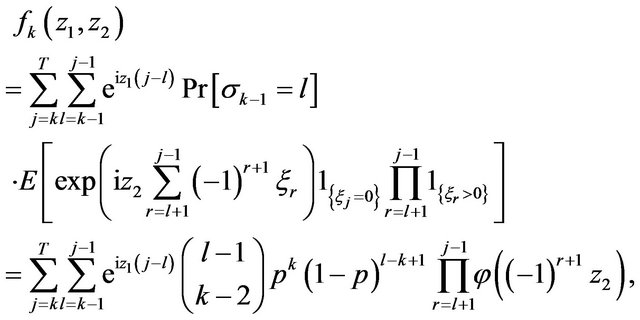
where 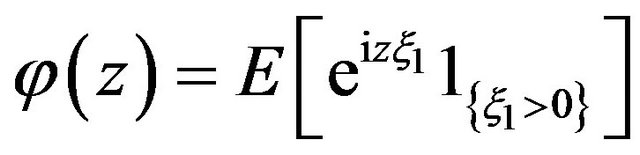 as above. After the changing the order of summation and summation indexes we have
as above. After the changing the order of summation and summation indexes we have
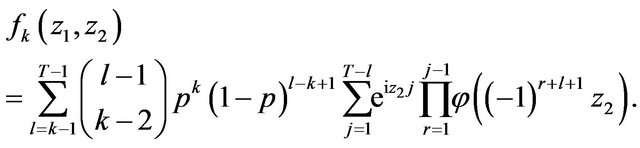
The same arguments as after Equality (3.8) lead to the following expression
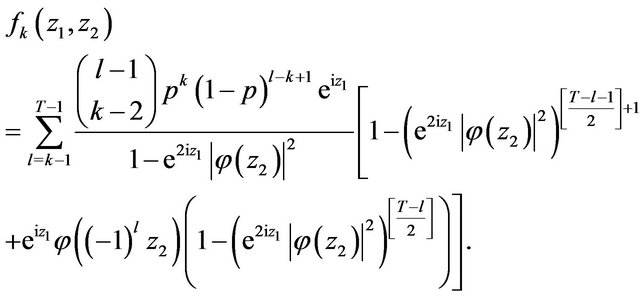 Now we consider one more simplest case.
Now we consider one more simplest case.
Recall the expressions for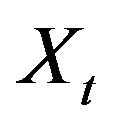 ,
, 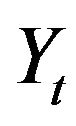 and
and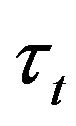 .
.
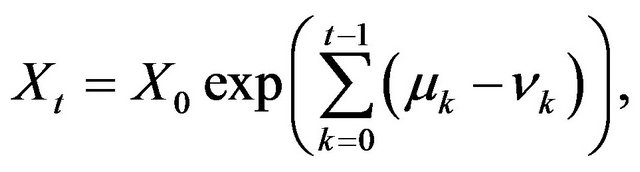

where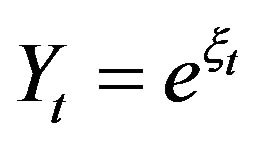 ,
, 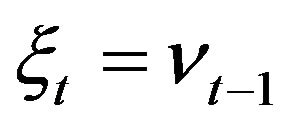 for
for 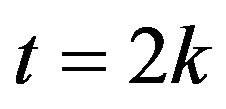 and
and 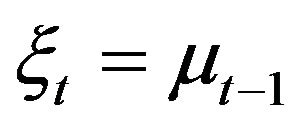 if
if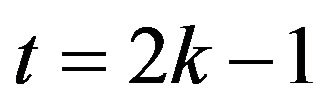 ,
,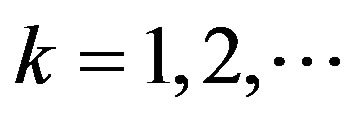 .
.
Assume that 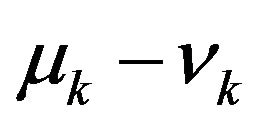 is a sequence of independent random variables. Then the power of exponent in the expression for
is a sequence of independent random variables. Then the power of exponent in the expression for 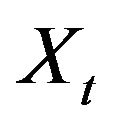 is a random walk and
is a random walk and 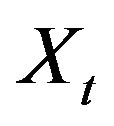 is a discrete analogue of geometrical Brownian motion, which is classical choice for modeling of the price process. But in our model the price process describes by
is a discrete analogue of geometrical Brownian motion, which is classical choice for modeling of the price process. But in our model the price process describes by , geometrical random walk computed at random time and the distributions of
, geometrical random walk computed at random time and the distributions of  and
and 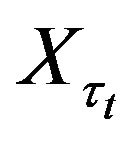 can be completely different. We show that indeed this is the case and the distribution of
can be completely different. We show that indeed this is the case and the distribution of  is trivial.
is trivial.
Denote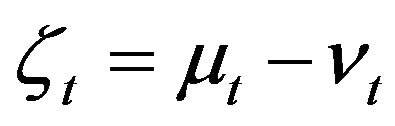 : then we have
: then we have

Since 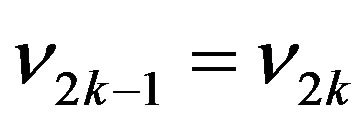 and
and 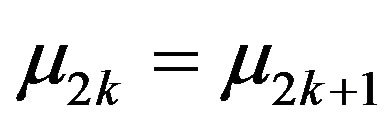 then
then
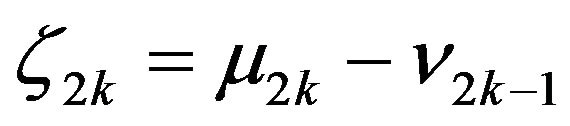 and
and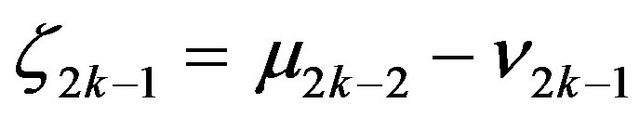 . Therefore
. Therefore
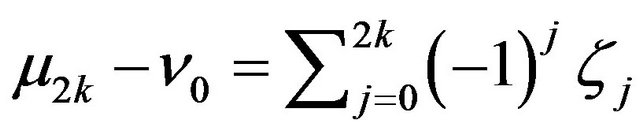 and
and 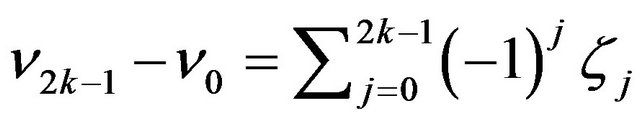
which implies the following equality:
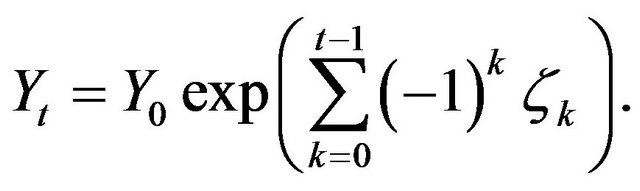 (3.9)
(3.9)
From the meaning of process 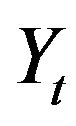 we have
we have 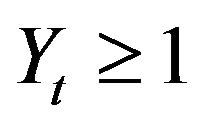 for all
for all 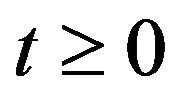 hence
hence  for any
for any 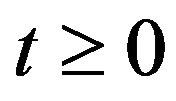 a.s. satisfy the following system of inequalities
a.s. satisfy the following system of inequalities
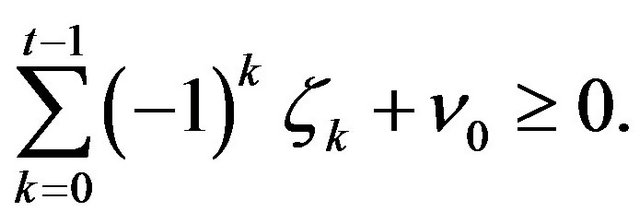
Denote the left side of the last inequality by
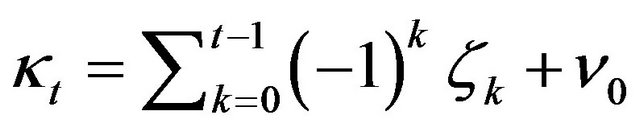 . Then
. Then 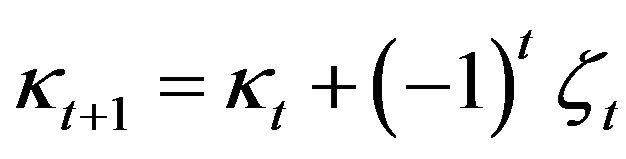 and
and
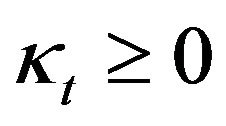 for all
for all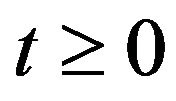 . It is evident that the random variables
. It is evident that the random variables 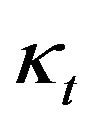 and
and  are independent and
are independent and 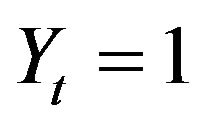 if and only if
if and only if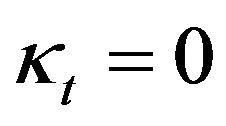 .
.
The following technical lemma will be needed.
Lemma 3.1. Let 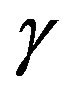 and
and  be two independent random variables. Then
be two independent random variables. Then
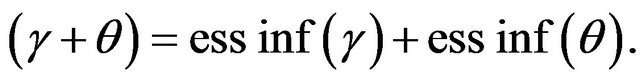
Proof. Recall the formula for distribution function of the sum of two independent random variables 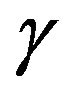 and
and 
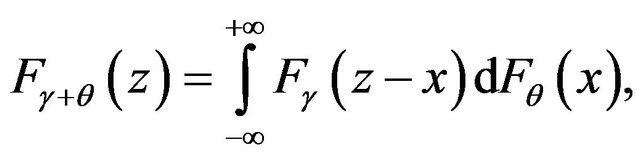
where  is the distribution function of the random variable
is the distribution function of the random variable . Since
. Since 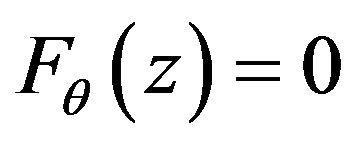 for all
for all 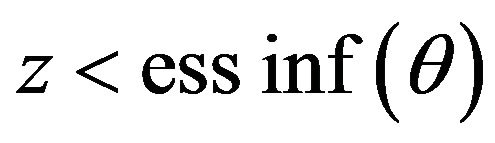 then
then
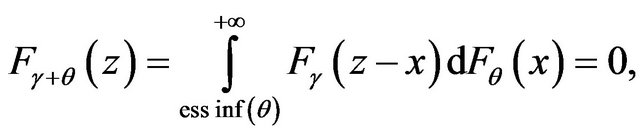
for all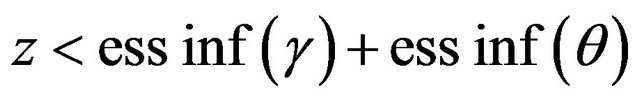 . This implies that
. This implies that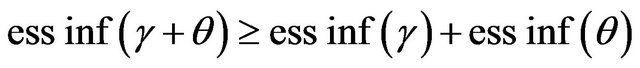 . Since the opposite inequality is obvious then we have the statement of the lemma.
. Since the opposite inequality is obvious then we have the statement of the lemma.
It follows from the non-negativity of 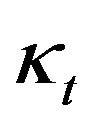 and lemma above that for all
and lemma above that for all 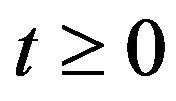
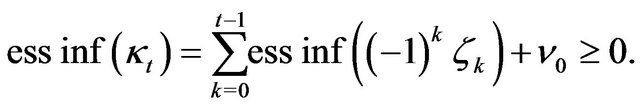
The trade occurs at time 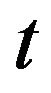 if and only if
if and only if , i.e. when the last inequality becomes in fact equality. In this case we have that
, i.e. when the last inequality becomes in fact equality. In this case we have that  for any
for any
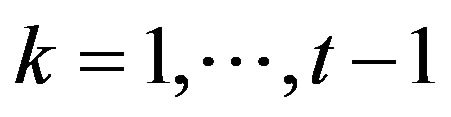 . Therefore
. Therefore
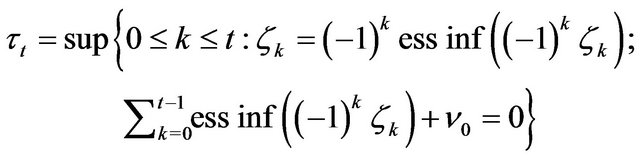
And the price of the last trade is deterministic and is equal to the following expression

In particular, if 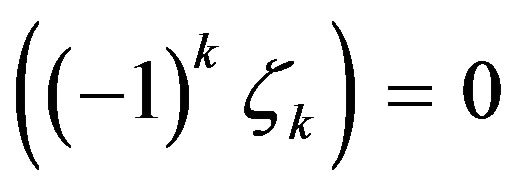 for all
for all 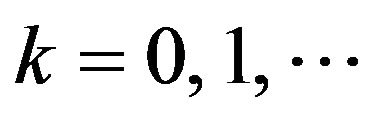
then 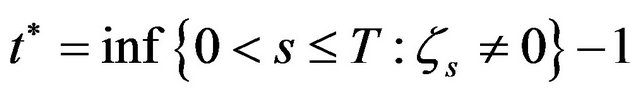 is a last possible moment of trade. There is a trade at each time
is a last possible moment of trade. There is a trade at each time 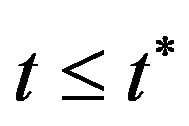 with the same price
with the same price 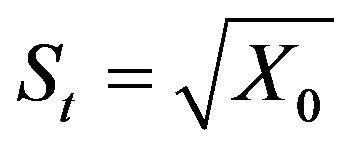 and there are no trades at all after the moment
and there are no trades at all after the moment .
.
4. The Connection to Continuous Time Analogue of the Model
In this section we give an example of the agents’ behavior such that the geometrical Brownian motion can be regarded as the limit of the price process 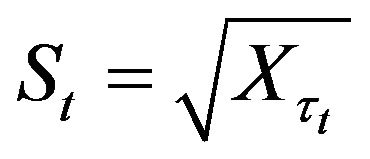 with discrete time
with discrete time . For this purpose let
. For this purpose let 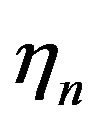 be a sequence of random variables describing the state of the real world (noise sequence). Assume that at each time
be a sequence of random variables describing the state of the real world (noise sequence). Assume that at each time 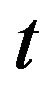 the agents make their decisions about how to change bid or ask prices according to the history of the noise sequence before the present time
the agents make their decisions about how to change bid or ask prices according to the history of the noise sequence before the present time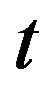 . For instance
. For instance 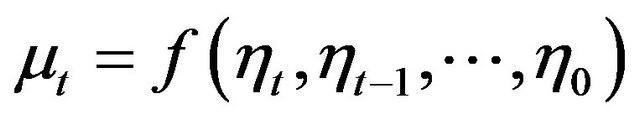 and
and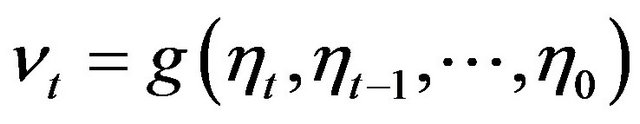 . The simplest case, with agents taking into account only the present value of noise
. The simplest case, with agents taking into account only the present value of noise 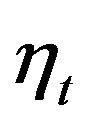 was considered above.
was considered above.
Now we consider the case when the agents are taking into account only the present 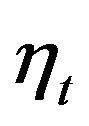 and previous
and previous 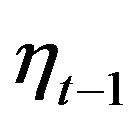 information,
information,  and
and 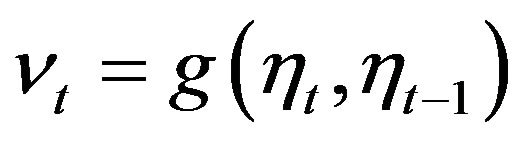 for even and odd moments. Assume that
for even and odd moments. Assume that 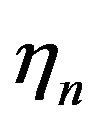 is a sequence of independent identically distributed random variables and set
is a sequence of independent identically distributed random variables and set 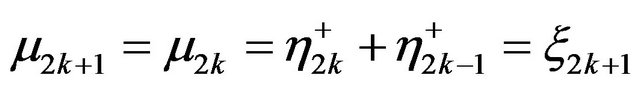 and
and 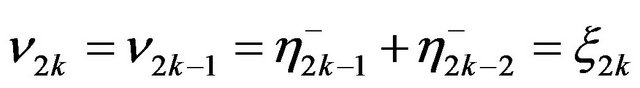 , where
, where 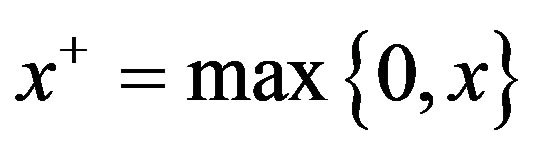 and
and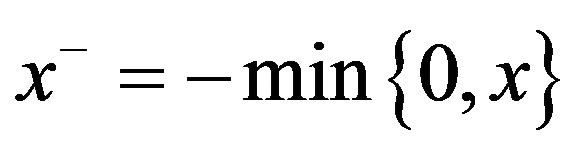 .
.
For such  and
and  we can compute the distribution of
we can compute the distribution of . For simplicity assume that
. For simplicity assume that 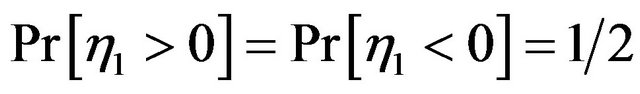 . If there are no trades then
. If there are no trades then
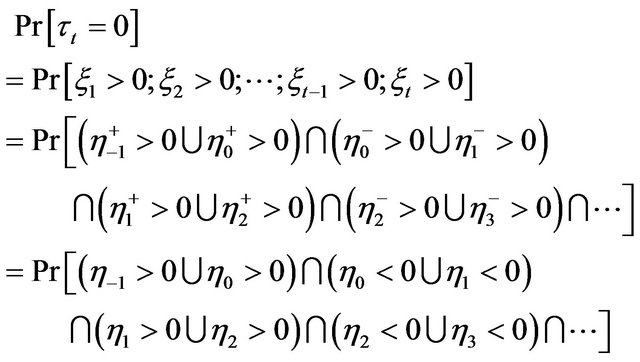
The last event happens if and only if the following condition is satisfied: for all  at least one of the numbers
at least one of the numbers 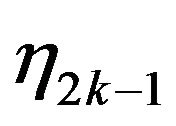 and
and 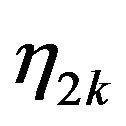 is positive and for all
is positive and for all  at least one of the numbers
at least one of the numbers 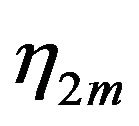 and
and 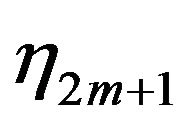 is negative. If
is negative. If 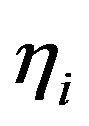 and
and 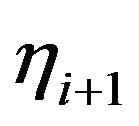 have the same sign then the sign of other
have the same sign then the sign of other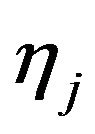 ,
,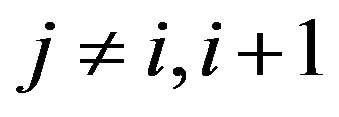 satisfying the condition above is uniquely determined. The condition above is also satisfied if
satisfying the condition above is uniquely determined. The condition above is also satisfied if 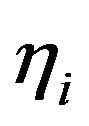 and
and 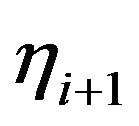 have the different signs for all
have the different signs for all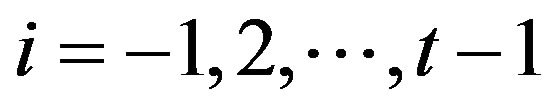 . Hence the number of possible choices of signs of
. Hence the number of possible choices of signs of 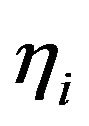 satisfying condition above is equal to
satisfying condition above is equal to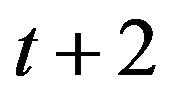 , where
, where 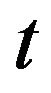 is a number of choices of
is a number of choices of 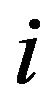 such that
such that 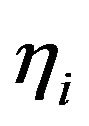 and
and 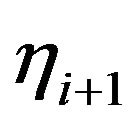 have the same sign and
have the same sign and  is number of possibilities that
is number of possibilities that 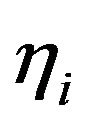 and
and 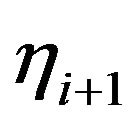 have the different signs for all
have the different signs for all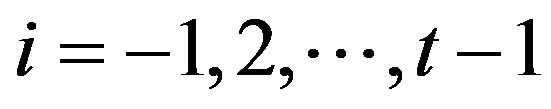 . Since for any choice of signs of
. Since for any choice of signs of 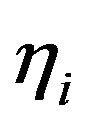 the probability is equal to
the probability is equal to  then we get
then we get
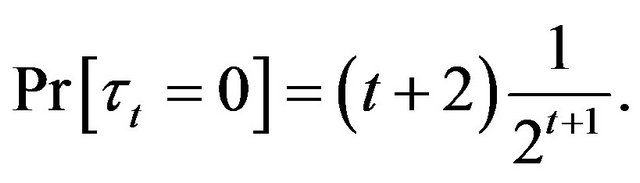
Notice that if 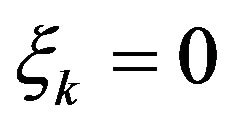 then
then 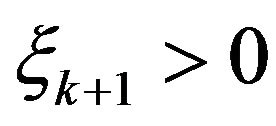 and
and 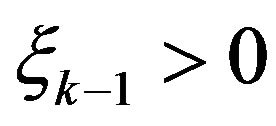 a.s. Indeed, for even
a.s. Indeed, for even 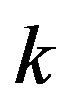 we have
we have 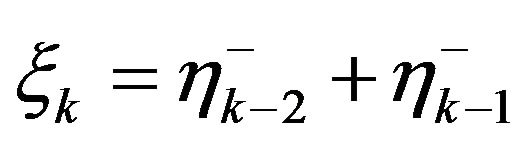 and since
and since 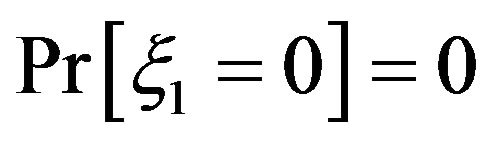 then
then 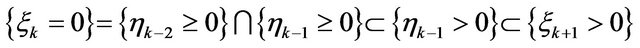 a.s. For odd
a.s. For odd 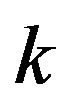 the proof is the same. The fact that
the proof is the same. The fact that 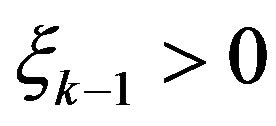 if
if 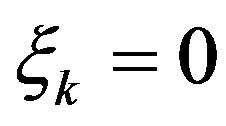 can be shown in the same way. Hence for
can be shown in the same way. Hence for  we get
we get

Now consider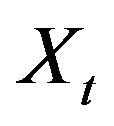 . From Equalities (3.3) and (3.4) we have
. From Equalities (3.3) and (3.4) we have
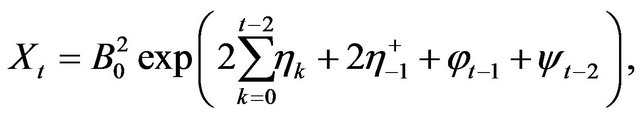 (4.1)
(4.1)
where 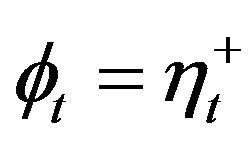 if
if 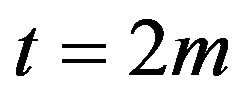 and
and 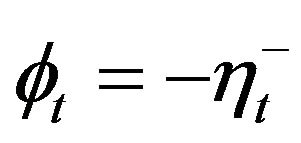 if
if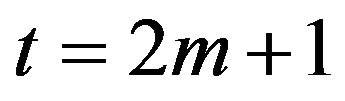 , and
, and 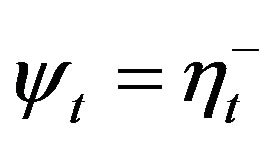 if
if 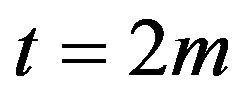 and
and  if
if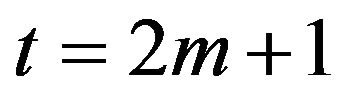 . Notice that the representation (4.1) is also true in the case when the random variables
. Notice that the representation (4.1) is also true in the case when the random variables 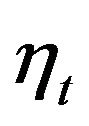 are not necessary independent and identically distributed. Since
are not necessary independent and identically distributed. Since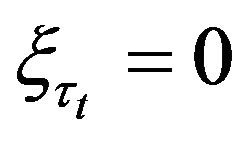 , then
, then  and from the last equation we deduce that
and from the last equation we deduce that
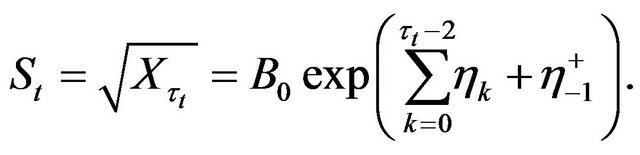
Let us compute joint characteristic function 
of the sum  and
and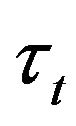 .
.
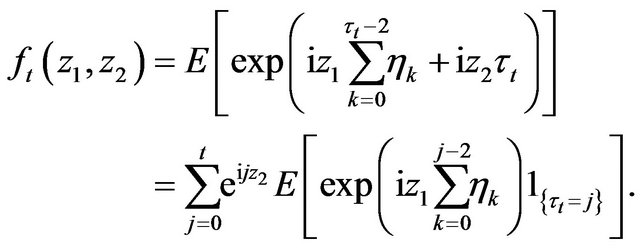
It has been shown above that
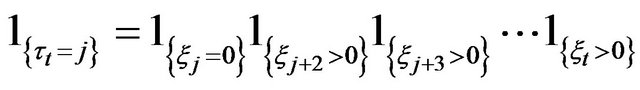 . Since
. Since  depends on
depends on 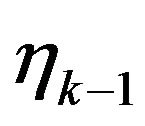 and
and 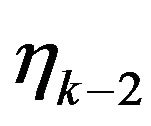 only then
only then
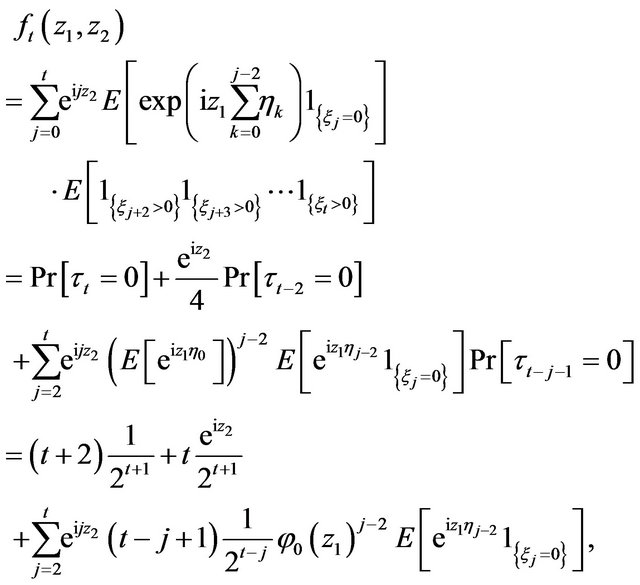
(4.2)
where 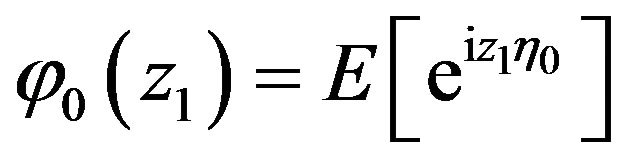 is the characteristic function of
is the characteristic function of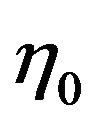 .
.
The expression 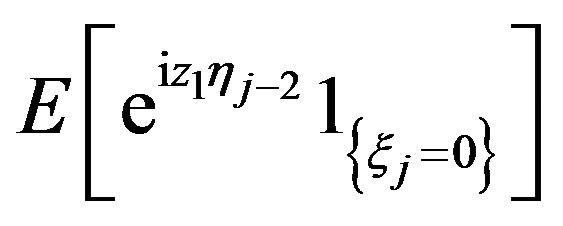 can be simplified as follows. If
can be simplified as follows. If  then
then 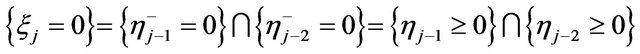 and
and
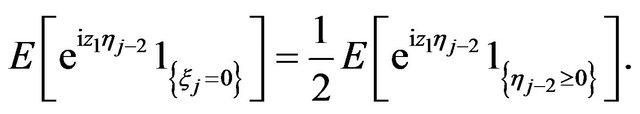
For 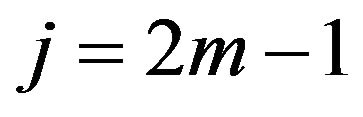 we have
we have  . Therefore
. Therefore
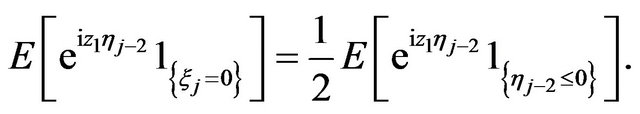
Then the Equality (4.2) has the following form
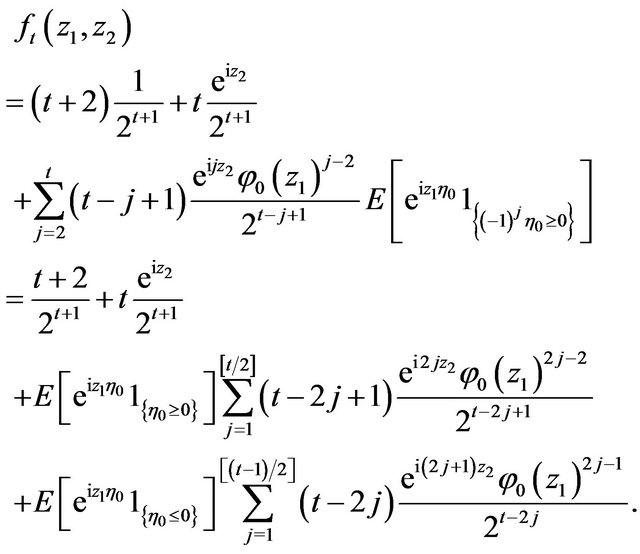
Suppose at first that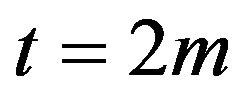 . Then from the last equality we get
. Then from the last equality we get
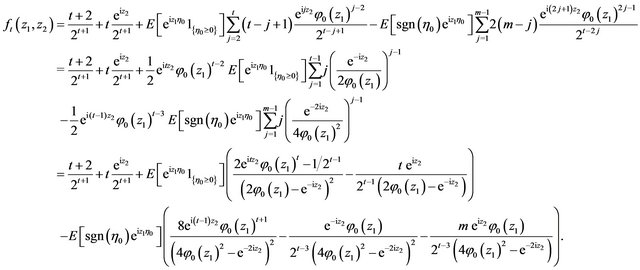
(4.3)
Similarly we have for 
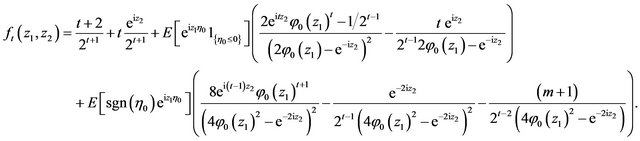 (4.4)
(4.4)
The last Equalities (4.3) and (4.4) allow one to obtain the characteristic function of a continuous time model analogous the process  as the limit of the discrete time model.
as the limit of the discrete time model.
For instance, consider the partition
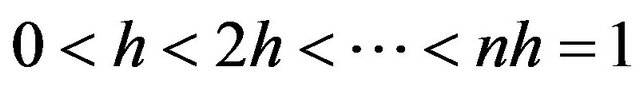 of the interval
of the interval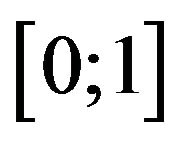 . Let
. Let 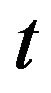 take values
take values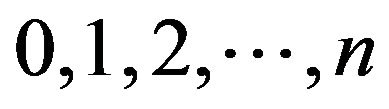 . Assume that
. Assume that  and
and
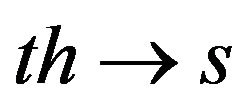 , where
, where . If the noise sequence
. If the noise sequence 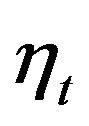 is Gaussian,
is Gaussian, 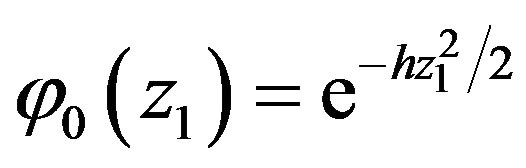 , then
, then
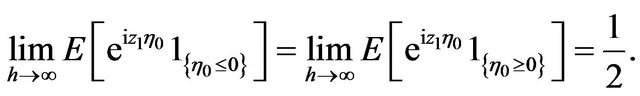
Hence from (4.3) and (4.4) we have
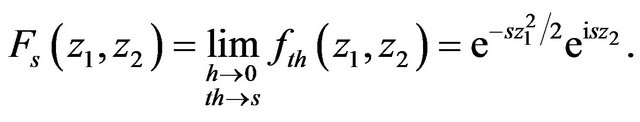
Therefore for Gaussian noise the continuous version of price process 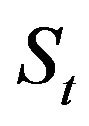 is a geometrical Brownian motion and
is a geometrical Brownian motion and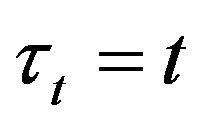 .
.
5. Conclusions
With this work we have set forth the structure for computing a price process from first principles of agent behavior in providing bid and ask quotes to a market. As well, we have provided some content by analyzing a basic case, that of a binomial assumption on the i.i.d. sequence  recording the moments of trades. This assumption led to the specification of a geometric random walk computed in random time, and to the joint characteristic function
recording the moments of trades. This assumption led to the specification of a geometric random walk computed in random time, and to the joint characteristic function  of the difference
of the difference
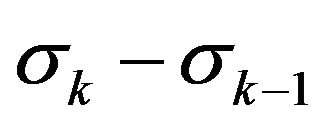 between moments of
between moments of 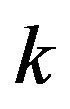 -th and
-th and  -st trades,
-st trades, 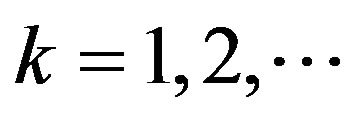 and the logarithm
and the logarithm 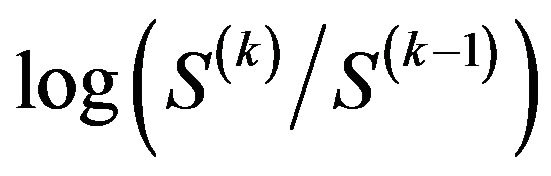
of the ratio between these trades. The study culminated with an explicit expression for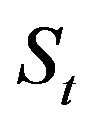 , and implications for a parallel model in continuous time.
, and implications for a parallel model in continuous time.
Next on the agenda is to explore alternative hypotheses on agent behaviors, and to perform simulations and other numerical work as necessary to establish a theory of consequential price processes.
REFERENCES
- A. Madhavan, “Market Microstructure: A Survey,” Journal of Financial Markets, Vol. 3, No. 3, 2000, pp. 205- 258. doi:10.1016/S1386-4181(00)00007-0
- H. R. Stoll, Elsevier/North-Holland, Amsterdam, 2003.
- O. E. Barndorff-Nielsen, “Processes of Normal Inverse Gaussian Type,” Finance and Stochastics, Vol. 2, No. 1, 1998, pp. 41-68. doi:10.1007/s007800050032
- E. Eberlein and U. Keller, “Hyperbolic Distributions in Finance,” Bernoulli, Vol. 1, No. 3, 1995, pp. 281-299. doi:10.2307/3318481
- T. Bollerslev, “Financial Econometrics: Past Developments and Future Challenges,” Journal of Econometrics, Vol. 100, No. 1, 2001, pp. 41-51. doi:10.1016/S0304-4076(00)00052-X
- R. F. Engle, “The Econometrics of Ultra-High-Frequency Data,” Econometrica, Vol. 68, No. 1, 2000, pp. 1-22. doi:10.1111/1468-0262.00091
- R. F. Engle and J. R. Russell, “Autoregressive Conditional Duration: A New Model for Irregularly Spaced Transaction Data,” Econometrica, Vol. 66, No. 5, 1998, pp. 1127-1162. doi:10.2307/2999632
- J. Hasbrouck, “The Dynamics of Discrete Bid and Ask Quotes,” The Journal of Finance, Vol. 54, No. 6, 1999, pp. 2109-2142. doi:10.1111/0022-1082.00183
- O. Bondarenko, “Competing Market Makers, Liquidity Provision, and Bid-Ask Spreads,” Journal of Financial Markets, Vol. 4, 2001, pp. 269-308. doi:10.1016/S1386-4181(01)00014-3
- M. Schaden, “Quantum Finance,” Physica A, Vol. 316, No. 1-4, 2002, pp. 511-538. doi:10.1016/S0378-4371(02)01200-1
- S. Hermannn and P. Imkeller, “The Exit Problem for Diffusions with Time Periodic Drift and Stochastic Resonance,” Prepublication No. 01, Institut de Mathématiques Élie Cartan, Université Nancy 1, Lorraine, 2003.
- P. C. Kettler, O. M. Pamen and F. Proske, “On Local Times: Application to Pricing Using Bid-Ask,” Preprint #13, University of Oslo, Oslo, 2009. www.paulcarlislekettler.net/docs/Oliv.pdf
- G. Di Nunno, B. Øksendal and F. Proske, “Malliavin Calculus for Lévy Processes with Applications to Finance,” Universitext, 2nd Edition, Springer, Berlin, 2009.
[15] NOTES
[16]
[17] *The work of Aleh L. Yablonski was supported by INTAS grant 03-55- 1861.
[18] 1For a treatment of the case wherein the duration, defined as the length of time between trades, is stochastic, see [14].
[19]

