Open Journal of Marine Science
Vol. 2 No. 4 (2012) , Article ID: 23802 , 16 pages DOI:10.4236/ojms.2012.24014
Application of Multivariate Geostatistics to Investigate the Surface Sediment Distribution of the High-Energy and Shallow Sandy Spiekeroog Shelf at the German Bight, Southern North Sea
1INTERCOAST, University of Bremen, Bremen, Germany
2MARUM, University of Bremen, Bremen, Germany
3Senckenberg Institute, Wilhelmshaven, Germany
Email: emeilianda@gmail.com, khuhn@marum.de, dedy_alfian@yahoo.com, Alexander.Bartholomae@senckenberg.de
Received May 1, 2012; revised June 5, 2012; accepted July 18, 2012
Keywords: Multivariate Geostatistics; Cokriging; Median Grain-Size; Bathymetry; Shallow Shelf; Mapping
ABSTRACT
Surface sediment data acquired by the grab sampling technique were used in the present study to produce a high-resolution and full coverage surface grain-size mapping. The objective is to test whether the hypothetically natural relationship between the surface sediment distribution and complex bathymetry could be used to improve the quality of surface sediment patches mapping. This is based on our hypothesis that grain-size characteristics of the ridge surface sediments must be intrinsically related to the hydrodynamic condition, i.e. storm-induced currents and the geometry of the seabed morphology. The median grain-size data were obtained from grab samples with inclusive bathymetric point recorded at 713 locations on the high-energy and shallow shelf of the Spiekeroog Barrier Island at the German Bight of the Southern North Sea. The area features two-parallel shoreface-connected ridges which is situated obliquely WNW-SSE oriented and mostly sandy in texture. We made use the median grain-size (d50) as the predictand and the bathymetry as the covariable to produce a high-resolution raster map of median grain-size distribution using the Cokriging interpolation. From the cross-validation of the estimated median grain-size data with the measured ones, it is clear that the gradient of the linear regression line for Cokriging is leaning closer towards the theoretical perfect-correlation line (45˚) compared to that for Anisotropy Kriging. The interpolation result with Cokriging shows more realistic estimates on the unknown points of the median grain-size and gave detail to surface sediment patchiness, which spatial scale is more or less in agreement with previous studies. In addition to the moderate correlation obtained from the Pearson correlation (r = 0.44), the cross-variogram shows a more precise nature of their spatial correlation, which is physically meaningful for the interpolation process. The present study partially contributes to the framework of habitat mapping and nature protection that is to fill the gaps in physical information in a high-energetic and shallow coastal shelf.
1. Introduction
Seabed habitats have a natural relationship with their environmental conditions. It is a spatially defined area where the physical, chemical, and biological environment is distinctly different from the surrounding environment [1]. Habitat scale refers to the geographic extent of a distinct biological community or geological features. The physical environment of a seabed habitat is defined by the interaction of the sediment and hydrodynamic flow as an agent of natural disturbance. Together with the effects of benthic organisms on this interaction they create the core of benthos-sediment coupling, which is essentially important in benthic habitat mapping [1].
Studies concluded that for macro-benthic organisms and demersal fish, one of the most important physical environments of the habitat is the seabed surface sediments [2-4]. For this reason, surface sediment distribution has been adopted in various seabed habitat monitoring studies as an important parameter to explain and predict the occurrence of macro-benthic habitat [1,5-8].
The physical environment for biotic habitat in the high-energy and shallow-water coastal shelves consists of very dynamic and complex large seabed features such as sand banks, sand waves, shore-connected ridges and flat surface [6-12]. Sandy patches commonly accentuate the surface of such seabed features. The sorting of sediments and their grain-size compositions are created under the influence of certain hydrodynamic conditions imposing the associated complex bathymetry; e.g. [5,6,8,11]. Significant change of this physical environment will ultimately influence the structuring of fish community, such as demersal and pelagic fish [8,13,14]. For this reason, among other most important points in creating benthic habitat mapping from a survey data collection is to confidently interpret properties of surface sediments. The degree of uncertainty of the interpretation determines the reliability of the resulting habitat maps.
On the other hand, particularly in shallow-water (<30 m) high-energy environments, knowledge of spatial relationships among benthic biota and sedimentary features has been severely limited by sampling technology [5,8]. Most sampling and surveying methods of benthic habitat mapping provide either high-spatial resolution over a small coverage area or low-spatial resolution over a large coverage area, given the economical constraint of habitat monitoring campaigns. In an ideal case, to achieve an ecologically meaningful habitat mapping, for instance, to monitor the influence of physical processes on habitat dynamics, the whole habitat system should be spatially covered while at the same time maintaining high resolution sampling points, for instance, of the type of sediments, benthic fauna or flora, etc. This is, however, rather difficult to achieve from the field surveys, particularly in the high-energy shallow sandy shelves such as the one in front of the Spiekeroog Barrier Island at the German Bight of the North Sea. The present study exemplifies the possibility of surface sediment data acquired by the grab sampling technique to be used in producing a high-resolution and full coverage surface grain-size mapping. Despite conventional, on the positive side, grab sediment sampling offers a fairly highly informative data on sediment particle size, compared to a descriptive sediment classification interpreted from a small-coverage, otherwise costly, side-scan sonar or multi-beam techniques.
Multivariate geostatistics have been used to obtain detailed and high-quality maps of the median grain-size distribution of sand fraction in the large coverage area of the Belgian Continental Shelf; e.g. [6]. Kriging with an external drift (KED) was used with additional secondary information to assist in the interpolation. The result of this extensive study is principally promising as it has demonstrated more realistic surface sediment distribution compared to that using univariate ordinary kriging [6]. It separates clearly the sediment distribution over the largescale seabed features such as the sandbanks from the swales. However, the secondary data must be available at all primary data locations as well as at all locations being estimated. The present study attempts to apply an alternative of multivariate geostatistics method for point interpolation, Cokriging, to produce a high-resolution median grain-size distribution map. The general aim is to test whether the hypothetically natural relationship between the surface sediment distribution and complex bathymetry could be used to improve the quality of surface sediment mapping. This is based on our hypothesis that grain-size characteristics of the surface sediments must be intrinsically related to the hydrodynamic conditions (storm-induced currents) and the geometry of the seabed morphology. Also, for a sandy shelf environment, median grain-size percentage is an important parameter to explain and predict the occurrence of benthic organisms; e.g. [6,10]. In this study, we demonstrate better understanding of natural relationships between the median grain-size distribution and the degree of complexity of the seabed bathymetry through analysis of multivariate geostatistics can in a way produce a reliable and high spatial-resolution full coverage (raster) map of the surface sediments at the high-energy and shallow sandy Spiekeroog shelf at the German Bight of the Southern North Sea.
2. Datasets and Methods
2.1. Data Description
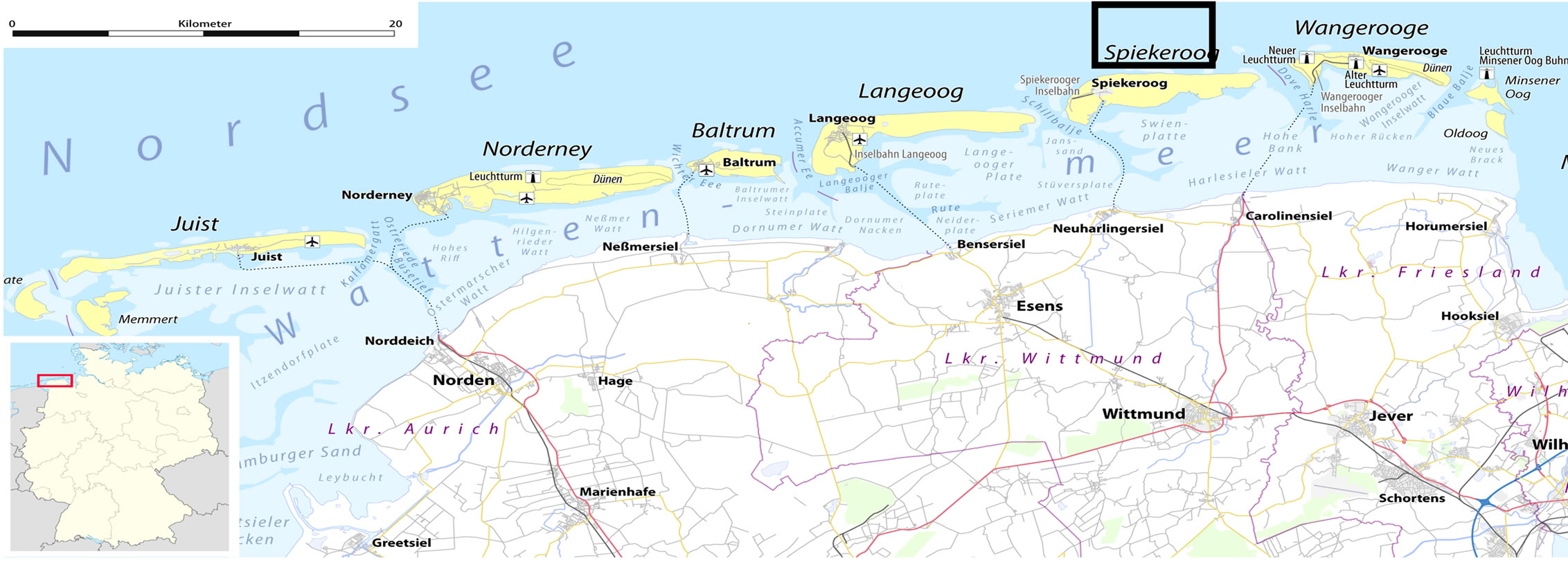
We made use the median grain-size data derived from the existing sedimentological database hosted by Senckenberg Institute in Wilhelmshaven for this study. The dataset is a compilation of sediment samples with inclusive bathymetric point recorded at 713 sample points using grab sampling technique at the shoreface of the Spiekeroog Barrier Island of the German Bight at the Southern North Sea (Figure 1(a)). The sediment sampling grids are of 500 × 500 m at the entire sampling area, except at a squared location at the nearshore which has denser grids of 250 × 250 m (Figure 1(b)). This data collection remains to be the largest sampling coverage and most detailed sampling campaign that has ever been conducted in this coastal region. The sampling of the whole 113 square-km coverage area was completed throughout the series of sampling campaigns between the year of 1986 and 1989. The area is a shallow sandy shelf featuring prominently large two-parallel shoreface-connected ridges which is situated obliquely WNW-SSE oriented and mostly sandy in texture (Figure 1(b)). The ridges heights were between 3 to 5 m with the slope angle from 0.5˚ to 1.0˚. The distance between the ridge crests was between 1 to 2 km away and located at the bathymetry of –10 to –18 m [12]. The sampling data are an excellent example of possible sampling technique feasible to be carried out in a shallow sandy coastal shelf area, particularly in terms of economical point of view.
The samples were undergone wet-laboratory treatment and further analyzed for grain-size distribution performed with an automated settling tube at the Sencken-
 (a)
(a) (b)
(b)
Figure 1. Location of the study. (a) Spiekeroog Barrier Island situated at the southern North Sea of Germany; (b) Map of grab sampling points of surface sediments at the Spiekeroog shelf with the overlaying bathymetric contour map. The grids of sampling points are 500 × 500 m, and 250 × 250 m at a location nearshore.
berg Institute [12]. Herein, the samples were analysed in 0.25 phi scale intervals between –1.25 to 4.00 phi (size range ca. 2.38 to 0.063 mm). We further sorted the dataset into percentage of grain-size distribution and picked up the size ranges that falls on the 50% to get the median grain-size (d50). The grab samples are accompanied with the bathymetric measurements at each sampled location (Figure 1(b)).
2.2. Geostatistics Application for Coastal Sedimentary System
The major key point of consideration herein is to select the appropriate interpolation method which makes use the natural relationship between the median grain-size of the surface sediment and the attributed bathymetry in order to produce a physically meaningful data interpolation. There are many ways to do interpolation, includeing the straight-forward deterministic methods (e.g. Nearest Point, Moving Average, Trend Surface and Moving Surface), geostatistical methods (e.g. different types of Kriging), and multivariate geostatistics methods (e.g. Kriging with External Drift, Co-Kriging) [15]. Unlike the straight-forward principal applied for the deterministic interpolations, geostatistical interpolation techniques (e.g. Kriging) have the advantage that they are involving randomness (stochastic). The latter predict an unknown value based on spatial variability of regionalized variables without an associated measure of uncertainty [16]. It makes use of the spatial correlation between neighbouring observations, to predict values at the unsampled places. Also, it provides a number of possible values with a probability of occurrence, thus, unique solution cannot be expected [16]. Nevertheless, when a single dataset expected to be highly variable but sparsely sampled, it is possible to include secondary information which is highly continuous into the interpolation. The latter can be done by using multivariate geostatistics technique. In this case, we use Cokriging technique.
Point interpolations assume spatial randomness of distributed input points which have a certain degree of spatial correlation between point values, and return regularly distributed point values [17]. In geo-information science, the input and output point values from an interpolation are depicted in maps. When a full coverage map was required as the output, the interpolation should be performed in a way of producing high-resolution return point values. Subsequently, it will be converted into a raster map, which is built from massive mosaic of smallest possible pixellete dimension of return values obtained from the interpolation. These are basically the principal methodology applies in this study to produce a highresolution map of the median grain-size distribution.
2.3. Spatial Correlation
Interpolation with Cokriging requires a known relation between the sparsely sampled variable (predictand) and the secondary variable (covariable) [16]. To come to this point, the spatial auto-correlation among the individual points in each dataset has to be analysed in advance. It examines the correlation of a random process with itself in space by geographical assumption that sample points that are closer are more alike than those farther apart [18]. In this way, we examined whether point values are spatially correlated, until which distance from any point this correlation occurs and whether point values have a certain direction towards each other (anisotropic). It is, therefore, clear that point interpolations assume a certain degree of spatial correlation between input point values [19].
2.3.1. Semi-Variogram Model
The experimental semi-variogram graph depicted in Figure 2 exemplifies the relationship in average between the calculated semi-variance and distance of point pairs. Semi-variogram model generates curve of continuous function which fits the discrete values of the experimental semi-variogram (Figure 2), which will give an expected value for any desired distance [20]. There are varying continuous function types applicable for semivariogram models. This includes Spherical, Gausian, Exponential, Power, Wave, Rational quadratic and Circular models; e.g. in [21,22]. This is an important step from which the parameters for kriging obtained; i.e. nugget, sill and range. These parameters will be acting as the nested models used in the interpolation by any type of kriging.
The semi-variogram 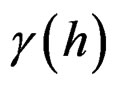 represents the average variance between observations separated by a distance h, which is estimated by [21]:
represents the average variance between observations separated by a distance h, which is estimated by [21]:
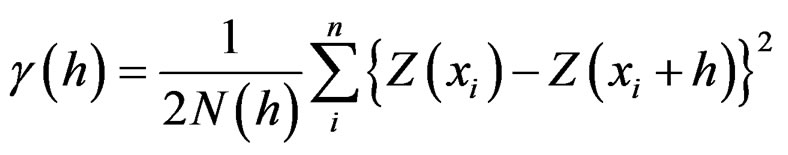 (1)
(1)
with 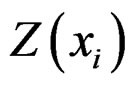 equal to the measurement at location
equal to the measurement at location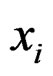 ,
,  the measurement at location
the measurement at location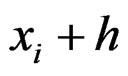 ,
,  the variogram for distance vector (=lag) h between measurements
the variogram for distance vector (=lag) h between measurements 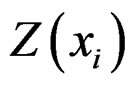 and
and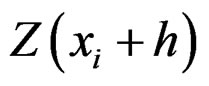 , the
, the  number of couples of measurements separated by h.
number of couples of measurements separated by h.
The semi-variogram graph explains the relationship between the point samples distances and their possible semi-variogram values. For instance, when the distance between sample points is 0, the difference between sampled values is also expected to be 0. Thus, the semi-
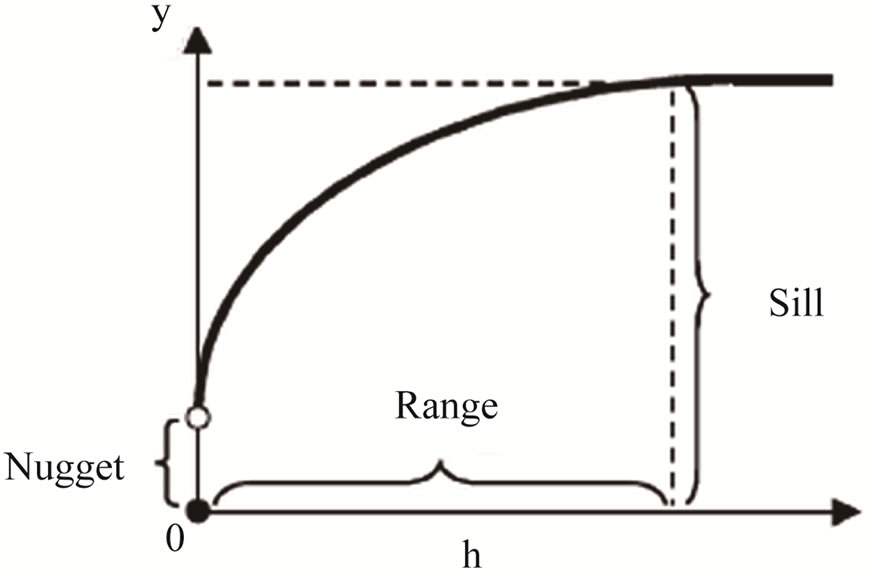
Figure 2. Example of a theoretical semi-variogram model. The dots are the experimental variogram and the curve represents the theoretical variogram [15].
variogram value 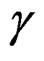 at distance 0 equals to 0, i.e.
at distance 0 equals to 0, i.e. . This implies that samples at a very small distance to each other are expected to have almost the same values; thus, the squared differences between sample values are expected to be small positive values at small distances. On the other hand, with increasing distance between point pairs, the expected squared differences between point values will also increase.
. This implies that samples at a very small distance to each other are expected to have almost the same values; thus, the squared differences between sample values are expected to be small positive values at small distances. On the other hand, with increasing distance between point pairs, the expected squared differences between point values will also increase.
At some distance the compared points that are so far apart are no longer related to each other, i.e. the sample values will become independent of one another. Then, the squared differences of the point values will become equal in magnitude to the variance of the variable. At this point, the semi-variogram no longer increases and the semi-variogram develops a flat region, called the sill. The distance at which the semi-variogram approaches the variance is referred to as the range or the span of the variable. When a semi-variogram contains a nugget effect, this indicates that the variable is erratic over very short distances, and/or that the variable is highly variable over distances less than the specified sampling interval (lag spacing) [15].
In the present study, the main focus of interpolation technique is the Cokriging which is a complex multivariate geostatistics method. To arrive at a conclusion of better interpolation technique, we will demonstrate the results of Cokriging, which accounts grain-size and bathymetry data as the variables, in comparison with Anisotropic Kriging, which only takes into the grain-size data. In principal, Cokriging is the multivariate variant of Ordinary Kriging. Anisotropic Kriging is also based on Ordinary Kriging, but makes use the additional anisotropic character belongs to the input data (e.g. median grain-size distribution) for the interpolation.
2.3.2. Cross-Variogram Model
Before Cokriging, cross-variogram analysis should be performed. The cross-variogram is defined as the variance of the difference between the predictand (median grain-size) and the covariable (bathymetry). As two variables are handled simultaneously, the cross-variogram operation can be seen as the multivariate form of the spatial correlation operation. It is a function of the distance and direction separating two locations, used to quantify cross correlation. Similar to the semi-variogram, crossvariogram generally increases with distance, and is described by nugget, sill, and range parameters [20].
Cross-variogram values are estimated directly from the sample data using the formula [23]:
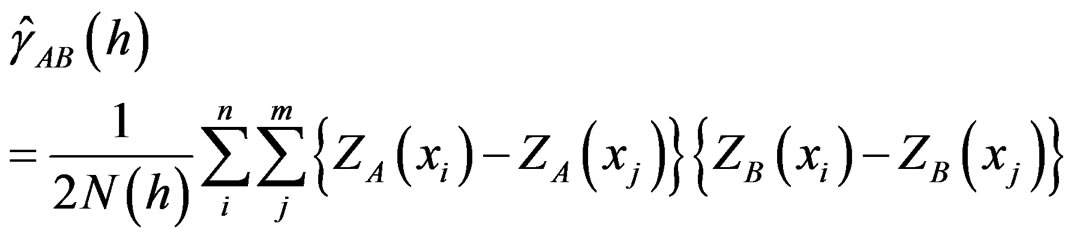 (2)
(2)
where 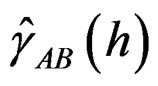 is the estimated cross-variogram value at distance h. This equation resembles the manner in which experimental semi-variogram values are computed in the spatial correlation operation with variable
is the estimated cross-variogram value at distance h. This equation resembles the manner in which experimental semi-variogram values are computed in the spatial correlation operation with variable  replaced by
replaced by 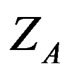 itself.
itself.
Cross-variogram values can increase to positive or decrease to negative values with distance h depending on the correlation between variable A and variable B [24]. Semi-variogram values on the other hand are by definition positive. The resulting parameters from the crossvariogram calculation will be fitted by model functions creating the cross-variogram curve for the combination of variables.
Before operating the cross-variogram, we need to check the cross-correlation between the two variables (predicttand and covariable) by calculating the Pearson correlation coefficient [24]:
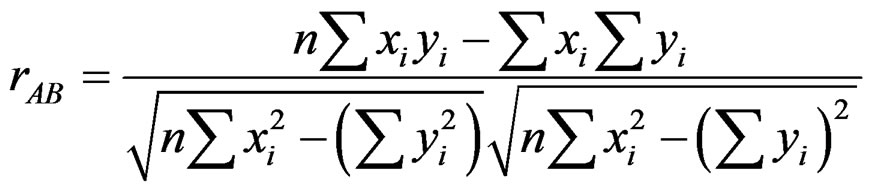 (3)
(3)
where 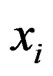 is the predictand value,
is the predictand value, 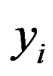 is the covariable value and n is number of samples. If x and y are measurements that contain measurement error, the realistic limits on the correlation coefficient are not –1 to +1 but a smaller range [24]. The Pearson correlation coefficient indicates the degree of linear correlation between two independent variables [6]. The closer the coefficient is to either −1 or 1, the stronger the correlation between the variables. If the variables are independent, Pearson’s correlation coefficient is 0.
is the covariable value and n is number of samples. If x and y are measurements that contain measurement error, the realistic limits on the correlation coefficient are not –1 to +1 but a smaller range [24]. The Pearson correlation coefficient indicates the degree of linear correlation between two independent variables [6]. The closer the coefficient is to either −1 or 1, the stronger the correlation between the variables. If the variables are independent, Pearson’s correlation coefficient is 0.
2.4. Interpolation Techniques
The estimations or predictions in Ordinary Kriging are calculated as weighted averages of known input point values (e.g. similar to the moving average technique). The estimate to be calculated, i.e. an output pixel value , is a linear combination of weight factors (
, is a linear combination of weight factors (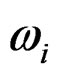 ) and known input point values (
) and known input point values (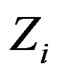 ) [23]:
) [23]:
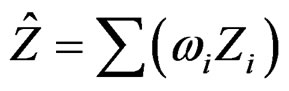 (4)
(4)
The weight factors of n valid input points i (i = 1, …, n) are found by solving the matrix equation for a set of n + 1 simultaneous equations:
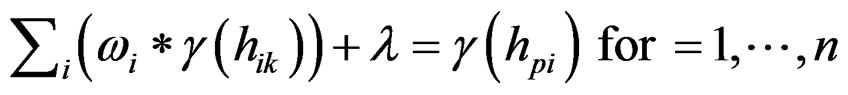 (5)
(5)
 (6)
(6)
where 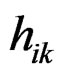 is the distance between input point I and input point k,
is the distance between input point I and input point k, 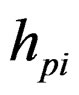 is the distance between the output pixel p and input point i,
is the distance between the output pixel p and input point i, 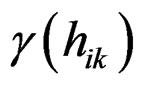 and
and 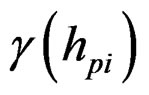 are the value of the semi-variogram model for the distance hik and hpi, respectively,
are the value of the semi-variogram model for the distance hik and hpi, respectively, 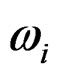 is a weight factor for input point i, and
is a weight factor for input point i, and  is a Lagrange multiplier, used to minimize possible estimation error.
is a Lagrange multiplier, used to minimize possible estimation error.
Equation (6) guarantees unbiasedness of the estimates. The solutions 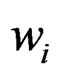 minimize the kriging error variance
minimize the kriging error variance 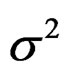 which calculates [23]:
which calculates [23]:
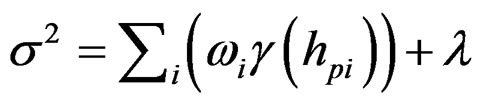 (7)
(7)
where 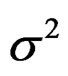 is the error variance for the output pixel estimate,
is the error variance for the output pixel estimate, 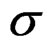 is the standard error which is the square root of the error variance.
is the standard error which is the square root of the error variance.
Cokriging is a statistical method based on the theory of regionalized variables and taking advantage of secondary observed values as the covariable to improve estimates (predictions) of the first variable [19]. It calculates estimates for a variable exhibits low spatial correlation (predictand; in this case grain-size samples), but likely to have some level of correlation with the one that shows relatively high continuity (covariable; in this case bathymetry). In Cokriging, the semi-variogram values of predictand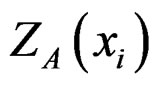 , covariable
, covariable 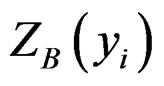 and the crossvariogram of A and B are used as the input parameters [22]:
and the crossvariogram of A and B are used as the input parameters [22]:
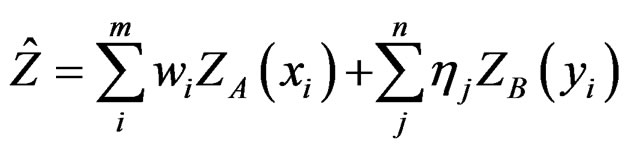 (8)
(8)
with its error variance is calculated as:
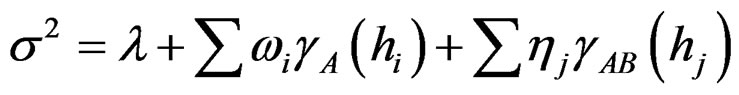 (9)
(9)
In this way it is possible to examine the autocorrelation for each of them and cross-correlation between them.
In GIS-based multivariate geostatistics module, Cokriging can be seen as a point interpolation, which requires a point map as input and which returns a raster map with estimations. Cross variogram calculates experimental semi-variogram values for two variables (the predictand and the covariable) and cross-variogram values for the combination of both variables. It is obviously a complex geostatistical technique and much more demanding than other kriging techniques. Thanks to the advanced GIS-based geostatistics technology which allows performance of these demanding tasks being done effectively, such as, ArcGISTM or ILWISTM which we were using in the present study.
In summary, besides the input point maps and also the Pearson correlation between the two variables (r), we need to specify the following parameters for the interpolation with Cokriging; 1) a semi-variogram model for the predictand; 2) a semi-variogram model for the covariable; and 3) a cross-variogram model for the combination of both variables. The resulting parameters of range, sill, nuggets and lag spacing from the most fitted crossvariogram model are used for the input parameters to interpolate with Cokriging.
2.5. Error Estimation
The most common method to evaluate the interpolation results quality, that is the difference between the estimated and the observed value, is a cross-validation [16, 19,25]. Cross-validation consists of removing data, one at a time, and then trying to predict it. The predicted value can subsequently be compared to the actual (observed) value to assess how well the prediction is working.
In the present study, we validate the interpolation result by evaluating some errors calculation using the Geostatistical Analyst which is embedded in ArcGISTM. The statistics of the errors are calculated by:
• Mean estimation error (MEE):
 (10)
(10)
MEE has to be about zero to have an unbiased estimator.
• Mean-square estimation error (MSEE):
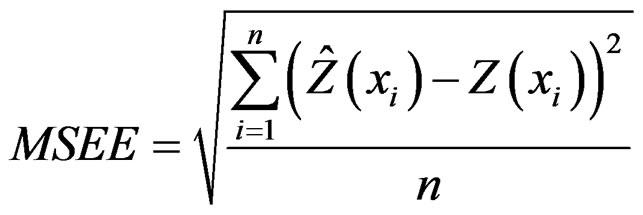 (11)
(11)
MSEE has to be as low as possible and which is useful to compare different procedures. The RMSEE is used to obtain the same units as the variable. This parameter has to be compared to the variance or the standard deviation of the dataset.
• Root-mean-square standardized estimation errors (RMSE):
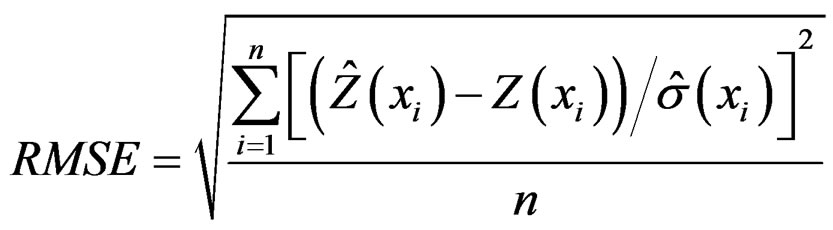 (12)
(12)
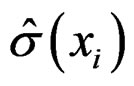 is the estimation standard error fort he location xi.
is the estimation standard error fort he location xi.
• Mean absolute estimation error (MAEE):
 (13)
(13)
MAEE is analogous to the MSEE, but less sensitive to extreme deviations.
• Confidence interval (CI):
 (14)
(14)
where 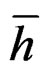 is the average distance from edge of all observations,
is the average distance from edge of all observations,  is the distance from edge, n is the total number of animal density observations and MSE is the residual mean squared error. From the combination of a krigged output map containing the estimates and its output error map, you can create confidence interval maps.
is the distance from edge, n is the total number of animal density observations and MSE is the residual mean squared error. From the combination of a krigged output map containing the estimates and its output error map, you can create confidence interval maps.
3. Results
3.1. Data Examination
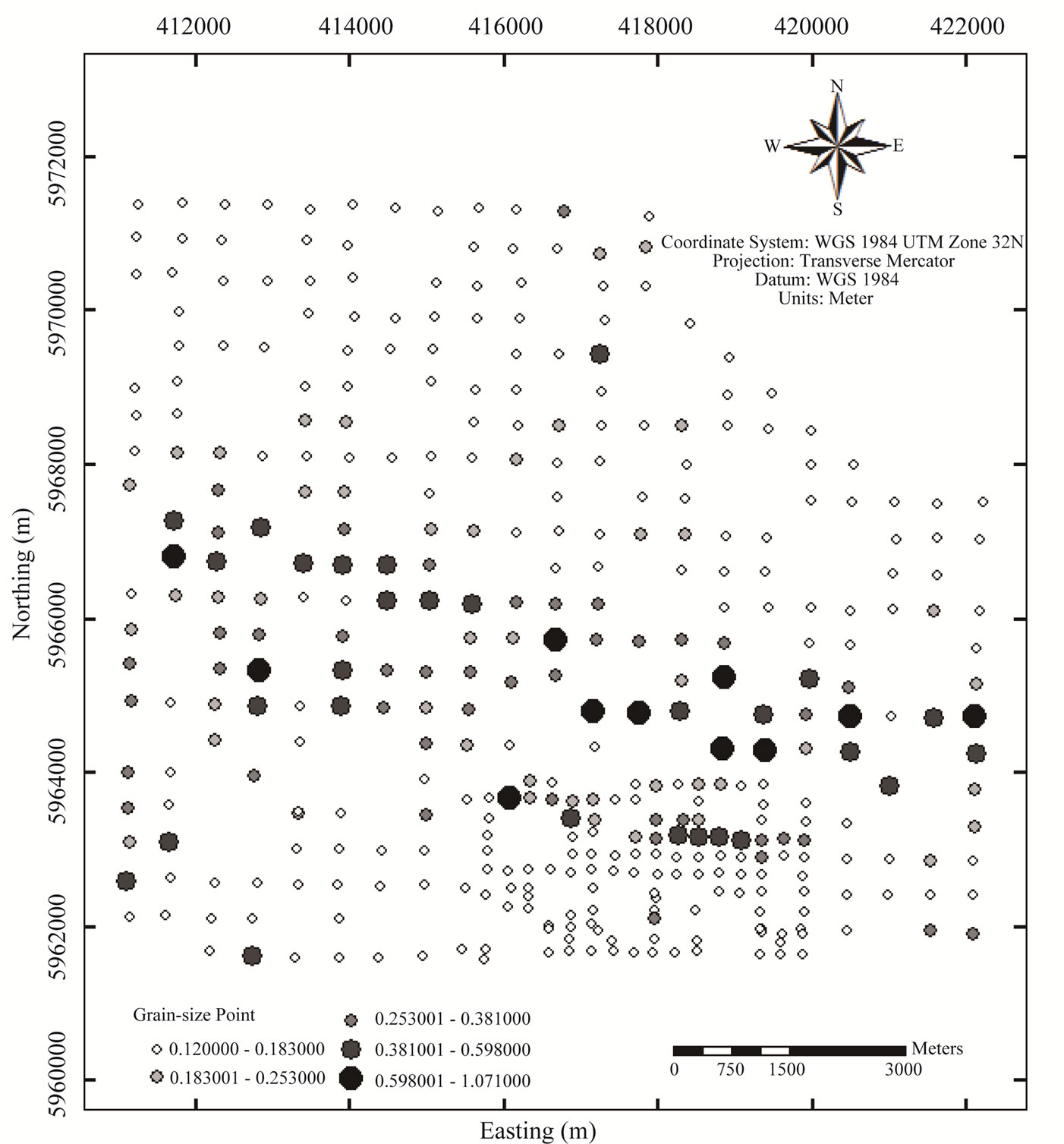
The present study makes use the median grain-size (d50) as the predictand and the bathymetry as the covariable to produce a high-resolution raster map of median grainsize distribution using the Cokriging interpolation. For evaluating the distribution and quality of the datasets, we performed descriptive statistical analysis (e.g. mean, median, standard deviation and spatial distribution) for both the median grain-size and bathymetry datasets. In this way we obtained the quality control of the sampled values, by assuming the samples inside the same zone are more similar than samples from different zones. On this basis, an insignificant number of outliers were randomly removed out of the median grain-size datasets, while no outliers was found in the bathymetric datasets. Before spatially analysed, 30% of well-distributed data points were extracted from each dataset. These small portions of datasets were used at a later stage to validate the resulting interpolation by cross-validation with the other 70% (see explanation in Subsection 2.3.2). Figure 3 depicted the 70% sample points of median grain-size and bathymetry, respectively. The Pearson correlation coefficient r between both variables is 0.44, indicating a moderately strong correlation.
3.2. Semi-Variogram Model
We used ILWISTM software to calculate the spatial autocorrelation of sample points in each datasets. We calculated the maximum diagonal distance of the sampled area to be approximately 14 km. By this distance the semivariogram was calculated using the 9 lags of 750 m spacing. This was based on the convention that the number and space of lags should not exceed half of the diagonal distance of the sampled area [6].
3.2.1. Median Grain-Size as the Predictand
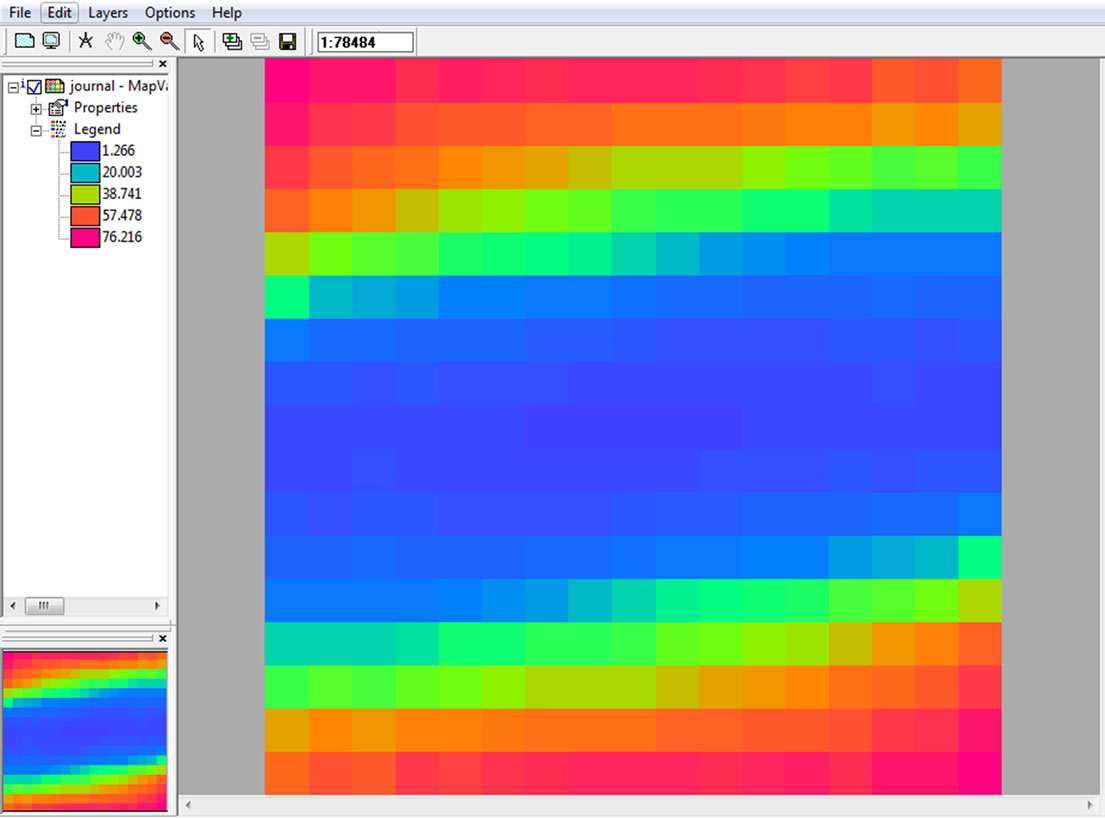
We can visually observe a certain directional tendency of the median grain-size distribution shown in Figure 3. We investigated such distribution characteristics using the variogram surface analysis, which result clearly shows anisotropy (Figure 4(a)). The pseudo colour of the variogram surface in Figure 4(a) indicates whether or not the semi-variogram values close to the origin of the output map. Each cell of the “raster” plot contains the semivariogram value for the specific distance class and the specific direction of the cell in relation to the origin of the plot where the distance and the direction are zero. Values of points which distances are very short are expected to be similar, which means that the semi-variogram values close to the origin of the output map is small. The blue raster cells are presenting this situation. The anisotropy revealed by the colour representation that gradually changed from blue (at the origin) to green and to red (away from the origin) in a certain direction going through the origin.
Since our median grain-size sample data shows anisotropy, the semi-variogram of the median grain-size data were calculated using the bidirectional method (normally using omni-directional method which considers all distances between point pairs). The semi-variogram values are calculated for the principle axis and the perpendicular “direction” of anisotropy with additional tolerance angle and band width (m). In this case, we assigned angle direction of 105˚ with angle tolerance of 45˚ and the bandwidth 3.
The graphs in Figures 4(c) and (d) show the experimental semi-variogram values (g) against the distance (h). We used ILWISTM software to select the parameters nugget, sill and range visually to fit the semi-variogram model curve to the experimental semi-variogram points. Further fine-tuning to fit the points were done by adjusting the parameters such as lag spacing, sill, range and nuggets manually. The final set of those parameters are subsequently used as the input for the interpolation. Two sets of semi-variogram model which represent the geometrical anisotropy were obtained. The parameter values of best-fitted Gaussian model of the median grain-size dataset obtained with a nugget of 0.004 mm2 and a sill of 0.02 mm2, with a range of 2000 m in the direction of the largest continuity (Figure 4(c)) and a range of 1300 m in the direction of the lowest continuity (Figure 4(d)).
The trend direction of the median grain-size distribution seems to have the largest continuity corresponding to the direction of the parallel shoreface-connected ridges (about 105˚ or trending WNW-ESE direction). This indicates that the sole grain-size data set has already shown the strong bathymetric influence on its spatial variability. Herein, we used ArcGISTM to carry out the interpolation by adopting the resulting semi-variogram model for the input parameters (nugget, sill and range). Figure 4(b) shows the result of the interpolation of the median grainsize of the surface sediments at the Spiekeroog shelf in 10 × 10 m pixel size resolution using the Anisotropic Kriging. It shows the directional tendency of the median grain-size distribution of the surface sediment which is expected to be associated with the parallel shorefaceconnected ridges at the Spiekeroog shelf. We calculated the estimation error of the interpolation (MEE) by comparing the predicted data with the measured data (the 30% taken-out data). The error results in merely 0.00005 which indicates a good performance of the modelling.
 (a)
(a)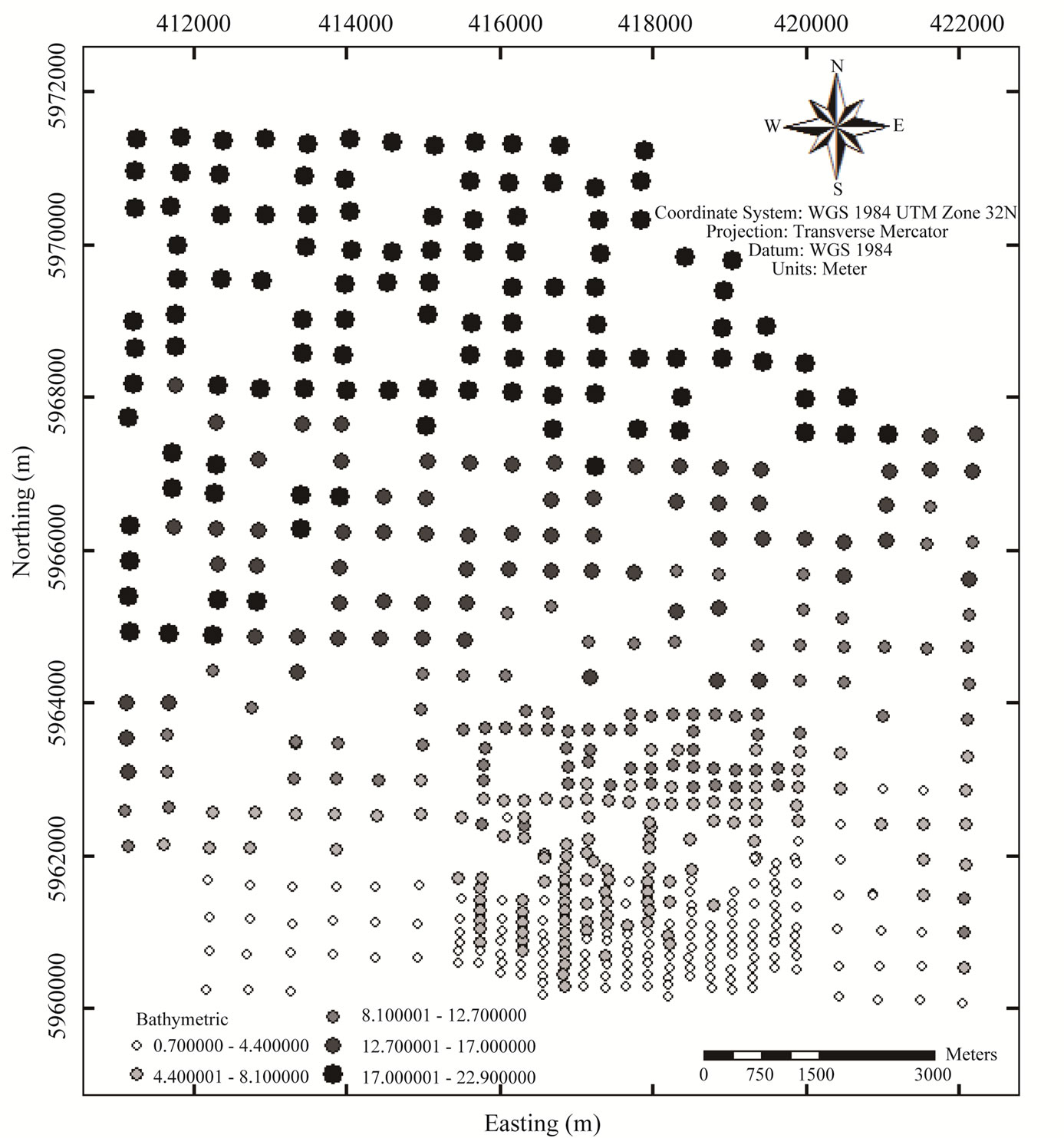 (b)
(b)
Figure 3. Sampling points used in the interpolation with Cokriging (70% out of the total sample population). (a) Sampling points of the median grain-size; (b) Sampling points of the bathymetry.
 (a)
(a)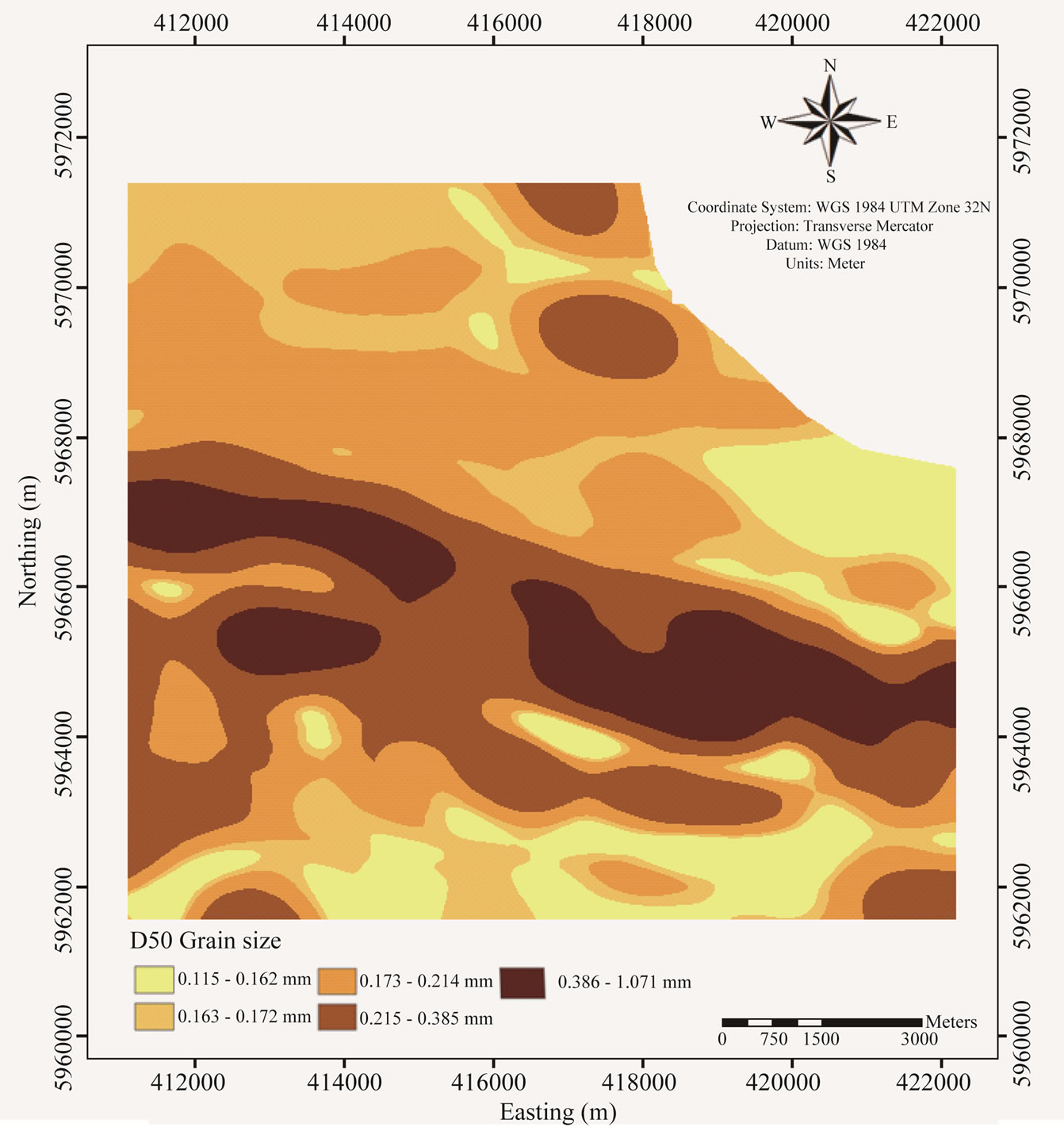 (b)
(b) (c)
(c)
Figure 4. Semi-variogram for the median grain-size. (a) Variogram surface showing a clear anisotropy; (b) The result of the interpolation of the median grain-size of the Spiekeroog in 10 × 10 m pixel size resolution using the Anisotropic Kriging; (c), (d) Experimental semi-variogram approached by Gaussian model with respectively the direction of the largest and the lowest continuity.
3.2.2. Bathymetry as a Covariance
Bathymetric data is generated into a set of Digital Elevation Model (DEM) as a means to provide the secondary variable (covariance) in the interpolation using Cokriging technique. This means that it has to demonstrate the highest possible continuity of the dataset and accuracy of the modelling prediction to enhance the interpolation of the predictand (median grain-size). Similar procedure to examine the spatial auto-correlation and semi-variogram calculation as for the median grain-size data was applied herein. The variogram surface result shows no anisotropy for our bathymetric data (Figure 5(a)) which was indicated by the low semi-variogram values (blue) that gradually increased from the origin into all directions.
In addition, the spatial auto-correlation of the bathymetry data shows a very good spatial correlation between the distance and the semi-variogram values (Figure 5(b)). After several experiments of semi-variogram, we obtained the parameter values of the median grain-size dataset which are best-fitted by the Gaussian model shown in Figure 5(b) with a negligible value of nugget and a sill of 180 m2 and a range of 11,000 m. We calculated the error of the model prediction as small as 0.01 m (Figure 5(a)).
After the semi-variogram parameters obtained, the interpolation was carried out using Ordinary Kriging, which is basically the uni-variate algorithm of the Cokriging (see principal equations used in Subsection 2.3). Based on the high performance interpolation, we generated a DEM for the bathymetry with spatial resolution of 10 × 10 m pixel size (Figure 6(b)). We calculated the interpolation result accuracy by comparing the 30% outtaken measured data points with the interpolation.
Result (Figure 6(a)). The error calculation of this interpolation procedure are listed in Table 1. The error values indicate the high quality interpolation results, that it can be used as the covariance for the interpolation to produce the reliable and high-resolution median grainsize distribution map with Cokriging.
3.3. Interpolation with Cokriging
We found that the best fitted modelling curve to fit the experimental cross-variogram is the Gaussian model (Figure 7(a)). Gaussian model creates the parabolic shape at the nugget of 0.0001 mm2, that it expresses a smooth spatial variation of the variables as it approaches the sill at the range of 1500 m. With this range, the median grain-sizes as a predictand and the bathymetry as the covariance tend to vary jointly and the spatial dependency is progressively decreasing as it approaches the cross-variogram points fitted to the flat curve (the sill) at 0.07 mm2. The flat region indicates that the dependency between the two variables is vanishing while still maintaining their own spatial auto-correlation. Beyond this distance (approximately starts at 9000 m) the cross-variogram shows a sharp descending towards negative values, indicating that the two variables (grain-size and bathymetry) have tendency to vary in opposite directions. Thus, the interpolation in the Cokriging will only use the strongest correlation between the median grain-size distribution and the bathymetry. These are the point values that fall within the range given for the best-fitted Gaus-
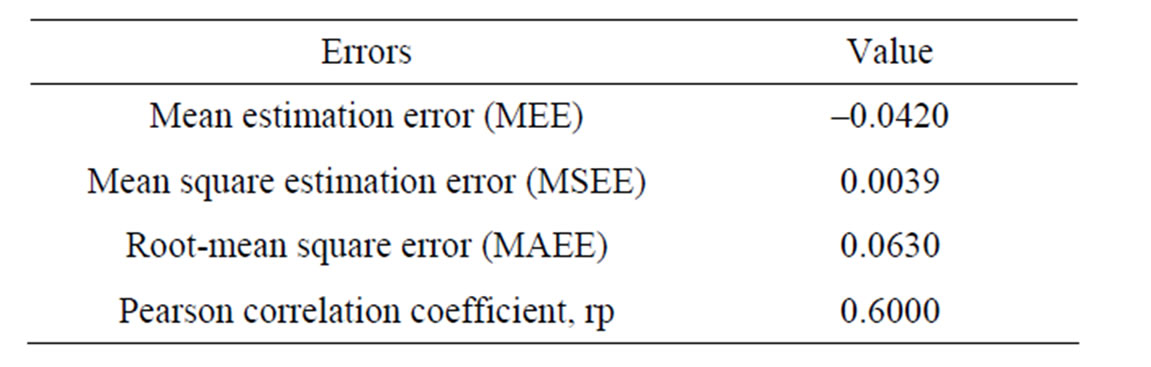
Table 1. Validation of the DEM of bathymetry using Ordinary Kriging interpolation.
 (a)
(a) (b)
(b)
Figure 5. Variogram experiment for the bathymetric data. (a) Variogram surface of the bathymetry datasets showing no anisotropy; (b) The spatial auto-correlation of the bathymetry shows a very good continuity.
 (a)
(a)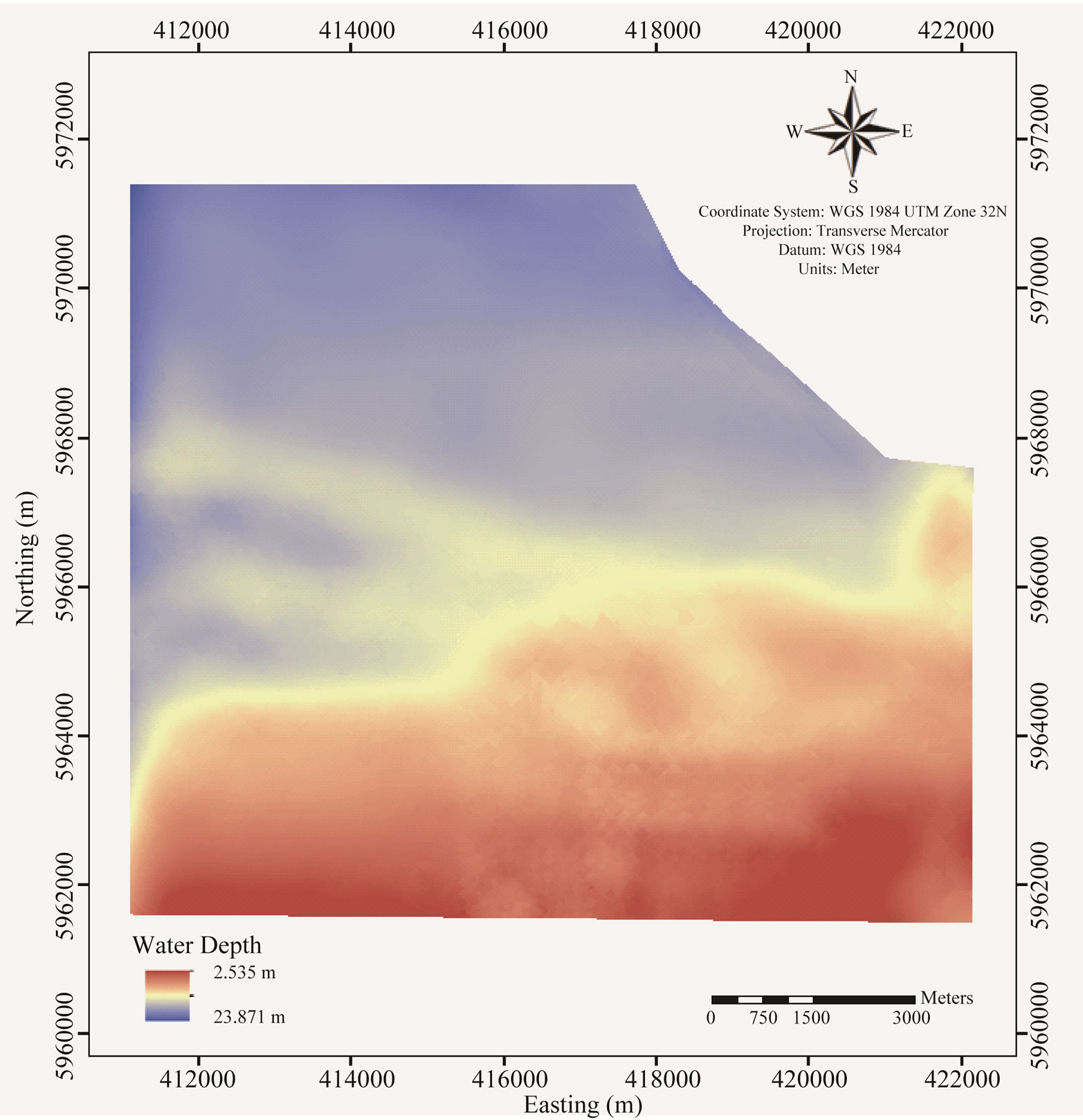 (b)
(b)
Figure 6. Interpolation of the bathymetry of the Spiekeroog using Ordinary Kriging. (a) The scatter plot of measured compared to estimated bathymetric value; (b) DEM result of bathymetry of 10 × 10 m pixel size.
sian model (1500 m). Using also the other parameter values, i.e. nugget and sill, we generated a raster map of 10 × 10 m pixel size by the interpolation with the Cokriging. The result is depicted in Figure 7(b).
4. Discussion
In this study, we developed an understanding of the spatial relationship between the surface median grain-size distribution and complex seabed bathymetry in highenergetic coastal shelf. Our analysis implies that relatively low-density median grain-size can be better interpolated when using the additional information of the continuously high-resolution bathymetry.
The Co-Kriging method has never been tested before in such a relatively small spatial coverage of high-ener-
 (a)
(a)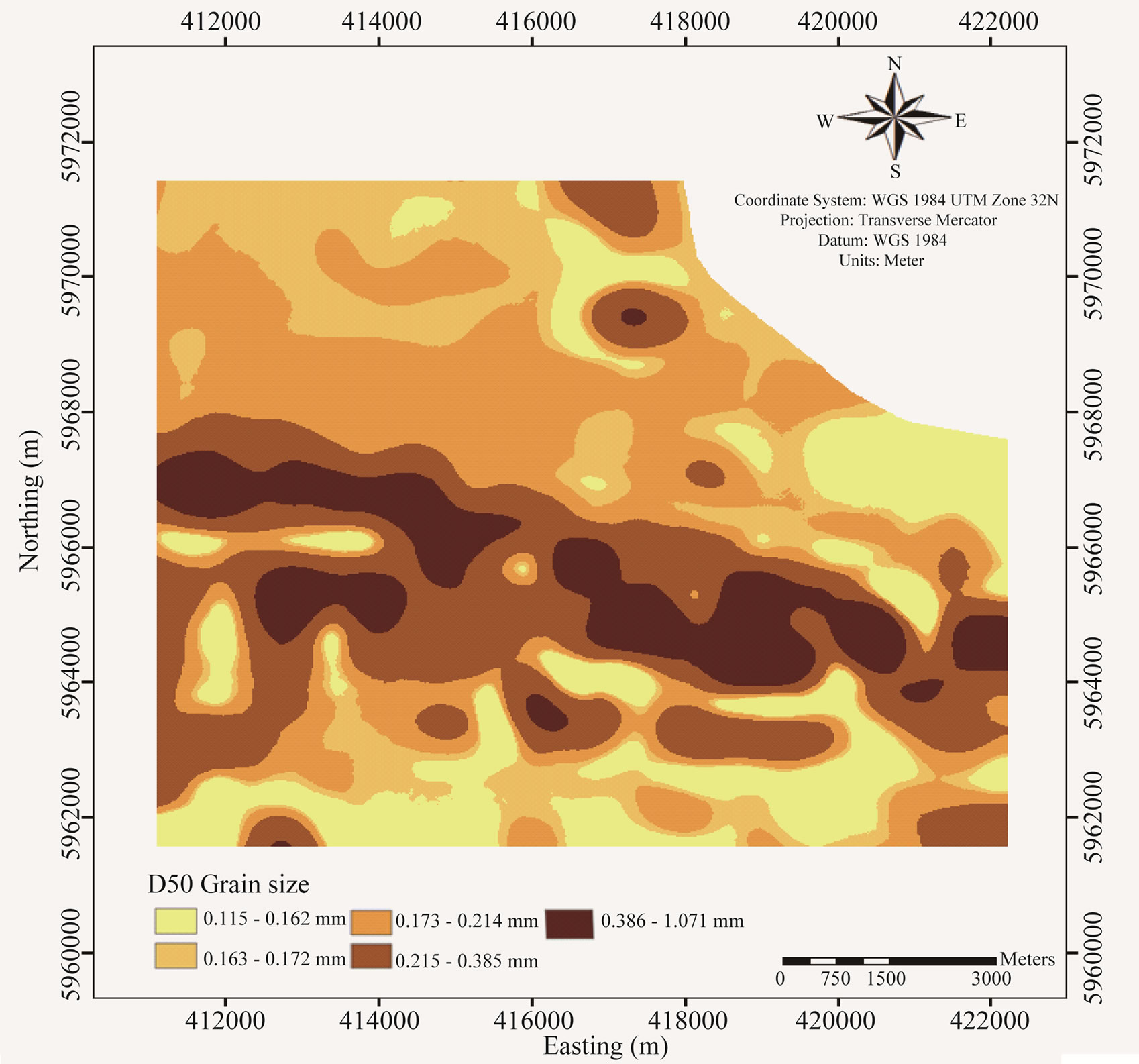 (b)
(b)
Figure 7. Interpolation of the median sediment grain-size of the Spiekeroog using Cokriging. (a) Experimental cross-variogram between the median grain-size (predictand) and the bathymetry (covariance) fitted by the curve of Gaussian model; (b) The final Cokriging map of median grain-size distribution.
getic and shallow coastal shelf. We adopted more or less similar basic principal of interpolation method for the large-scale Belgian Continental Shelf [6], in which they used Kriging with External Drift (KED).
The latter method uses the anisotropic character of the predictand which was described by the covariable (e.g. bathymetry). For our relatively small-scale of study area, we found that such multi-variate approach is rather redundant. This was because our bathymetry, as the covariable, was accentuated with merely two parallel shoreconnected ridges as the main seabed features. With such bathymetry (with additional smaller-scale abrupt changes in bathymetry), the resulting anisotropy of the surface sediment can be clearly observed in the median grainsize data alone, as can be seen in our interpolation result with Anisotropic Kriging (Figure 4(b)).
As a univariate geostatistics, interpolation with Anisotropic Kriging the interpolation was using the greater range in the direction of the largest continuity, i.e., along the parallel shore-connected ridges in Figure 4(c), while smaller range (Figure 4(d)) was used in the direction of the lowest continuity; i.e. perpendicular to the ridges orientation. Within each interpolation window (for both greater and smaller range), a local stationary is assumed. This is clearly not what we expected for surface grainsize distribution of the complex seabed morphology because it will create a smoothing effect, particularly in the direction of the anisotropy (Figure 4(b)). The chance that the interpolation “overlooks” the variability of grainsize distribution is high, when it solely dependant on the grain-size data alone. In addition, at the area where the samples were taken in denser grids (250 × 250 m) close to the shoreline the resulting variance was low compared to that of the sparsely sampled area. This implies that, whenever necessary, more samples should be taken in between the sparse sampling points for better mapping, for instance, for monitoring purposes.
Compared to the KED as a multi-variate geostatistics method, Cokriging gives more advantage for not requiring the secondary information (covariance) to be known at all locations being estimated [6]. Cokriging takes into account purely the spatial correlation between the predictant (e.g. median grain-size) and covariance (e.g. bathy-metry) without necessary a priory information about the “drift” of the data, which required by KED. This means that Cokriging can be applied to interpolate any chaotic situation of covariance (bathymetry) so long it has a true spatial relationship with the predictand. With this argument, we produced our detailed median grainsize map which clearly shows a more realistic pattern of sediment patches Figures 7(b) and 8.
Cross-variogram model is the most important elements in Cokriging because it describes the spatial correlation between the two considered variables. The relatively small range of the spatial correlation between the median grain-size and bathymetry shown in the experimental cross-variogram (Figure 7(a)) suggests a small variability of the spatial correlation between the two variables. In addition to the moderate correlation pertained from the Pearson correlation (r = 0.44), this shows a more precise nature of their spatial correlation, which is physically meaningful for the interpolation process. This is particularly invaluable information in case of mapping the surface sediment at the abruptly changing bathymetry. Because it provides the information of the locality in which correlation between the two variables is still valid in the pursuit of realistic interpolation.
From the cross-validation of the estimated median

Figure 8. Median grain-size distribution of the Spiekeroog shelf using Cokriging generated in 3D with the bathymetric information with 200 times vertical exaggeration.
grain-size data with the measured ones using the 30% out-taken datasets, it is clear that gradient of the linear regression line for Cokriging is leaning closer towards the theoretical perfect-correlation line (45˚) compared to that for Anisotropy Kriging (Figure 9). In comparison with the univariate Anisotropic Kriging, the interpolation result using Cokriging shows more realistic estimates on the unknown points of the median grain-size. This is shown by the slightly higher error values for Anisotropy Kriging compared to those for the Cokriging (Tabel 2). This gives the first indication that Cokriging provides better estimates.
Despite showing a positive relationship between median grain-size and bathymetry, the cross-variogram (Figure 7(a)) also shows the negative correlation values as the distance increases. This negative correlation indicates a cross-scale correlation between the grain-size and the bathymetry, that the two variables were positively correlated at a small-scale (<1500 m) and negatively correlated at a larger-scale (>1500 m). Such spatial correlation seems to be typically found in the marine habitat structures. The small-scale positive correlation found in the present study analogous to the relationship between macro-benthic diversity and soft-sediment habitat structure studied by [26], where they revealed that the macrobenthic diversity is typically determined by the smallscale sediment structure on the seafloor on the scale of 100 to 1000 m, which is basically the size of surface sediment patches shown in our Cokriging map. In addition, [14] reveals the positive relationship between macrozooplankton and fish biomass at the small scale indicates that, locally, fish concentrate at macrozooplankton patches, which scales are also relatively similar. This suggests that the Cokriging interpolation result can capture well the detail of patchiness of surface sediment described in the other study (e.g. Thrush et al., 2001).
On the other hand, the large-scale (negative) correlation was found in the case of correlation between macrozooplankton and fish biomass [14], similar to what we found in our cross-variogram analysis (Figure 7(a)). They observed that the negative relationship of the two variables observed on a large scale (i.e. large range distance) illustrates that fish and macrozooplankton are dis-

Figure 9. Cross-validation between the measured and the estimated median grain-size data using Anisotropic Kriging (right) and Cokriging (left).
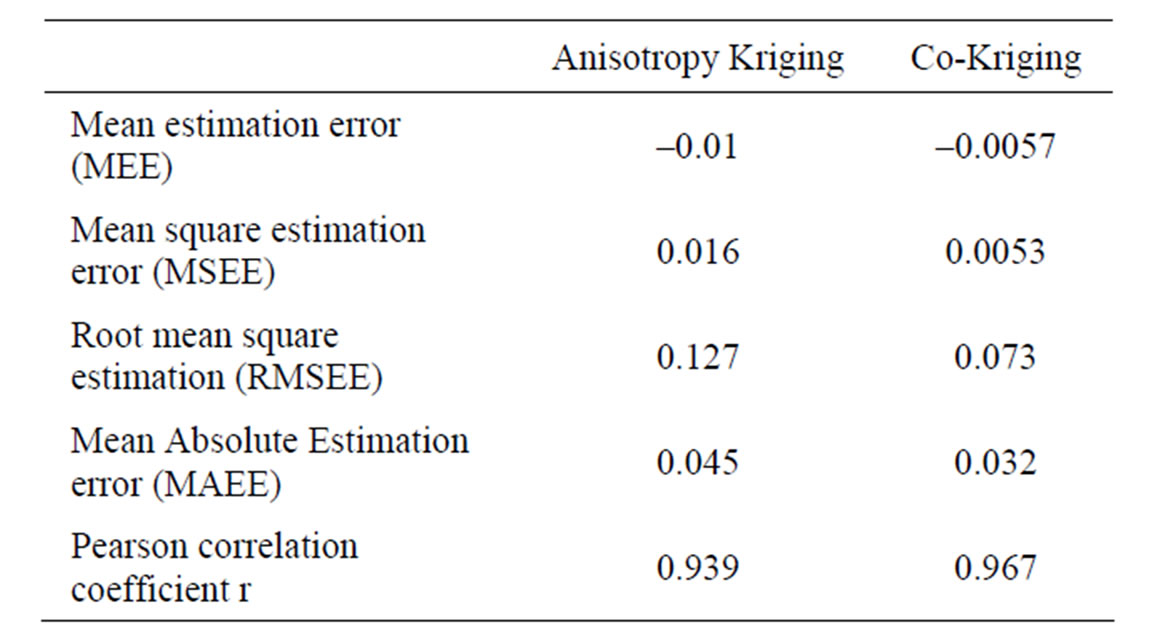
Table 2. Comparison of errors produced by Anisotropic Kriging and Cokriging.
tributed in different regions (inshore and offshore). These are probably analogous to the difference of sediment grain-size distribution at the seaward flank (fine sediment) from the landward flank (coarse sediment) in the present study (Figures 7(b) and 9). Zooplankton aggregations have a certain degree of permanence above seabed features such as seamounts, canyons and shelf-breaks [27, 28].
It is clear that by being able to describe the spatial relationship between the median grain-size and the bathymetry, one is in a better position to realistically estimate the unknown grain-size of sediments deposited, for instance, on the swales or at the landward flank of the ridges when very limited sediment grain-size data were sampled. The interpolation result with Cokriging shows that the finest sediment occurs on the seaward flanks while the coarsest sediment occurs on the swales and landward flanks (Figures 7(b) and 9), which are in a good agreement with the result of the previous study on the surface sediment distribution in the same area by [6, 11].
Naturally, the abrupt changes of bathymetry create highly localized surface sediment patches. The most logical explanation about the sediment patches is their formations influenced by the sediment transport processes under a certain hydrodynamic condition. This is particularly the case for the high-energy and shallow coastal shelf environment such as the Spiekeroog, because micro-biological effects on sediment leading to bioturbation are presumably negligible, since sediment transport events are intense and frequent [8].
Therefore, it is rightly assumed that the surface sediment patches predominantly determine the habitable conditions for the macro-benthic habitat in such environment.
Particularly for the Spiekeroog shelf, previous studies by [11] have shown a high rate landward migration of the shore-connected ridges of 80 m/year over a time span of 8 years, while the rates of storm-induced migration could be as high as 100 - 200 m/year. Of particular interest is the intensity of erosion at the swales could be as high as 500 m/year due to storm-induced currents. It is, therefore, interesting for the future outlook of the present study to investigate correlations also exists across different level of habitat structures and whether under the ever-escalated extreme-climatic driving force the large-scale seabed features such as the shore-connected sand ridges create a sheltered area for fish growth, providing the high-energetic storm-induced current.
Habitat maps demand is increasing for marine-spatial planning. The function of habitat mapping is not only used to help determining the dominant physical environment characteristics of the differences and boundaries between habitats living on the seabed surface, but the high resolution continuous coverage sediment distribution map can be used as the initial domain for habitat modelling under the certain hydrodynamic influence. However, there is no easy way to do so, particularly for the natural condition of the highly-energetic shallow sandy shelf. Grab samplings, therefore, remains as a good alternative in addition to the other remote sensing based technology such as side-scan sonar and multi-beam echo sounding. Althought rightly said that grab sampling method merely yield a much localized representation [8], it is possible nowadays to tackle this limitation by applying multivariate geostatistics analysis such that exemplified in the present study. This is particularly true if the natural relationship between at least two variables was known to be strong. Moreover, the highly informative data on sediment particle size is highly valuable to link to the types of biotic habitat that might occupy certain patches of sandy environment, or vice versa. As the influence of increasing storminess and anthropogenic activities becomes more apparent in the coastal region, it implies that any changes occur on the surface sediment structure will significantly decrease macro-benthic biodiversity, consequently that of the wider marine ecosystem. Therefore, continuous monitoring campaign of the seabed habitat is important. The present study partially contributes to the framework of habitat mapping and nature protection that is to fill in the gaps in physical information in a high-energetic and shallow coastal shelf.
5. Conclusion
Sandy patches typically accentuate the surface of seabed features. The sorting of sediments and their grain-size composition are created under the influence of certain hydrodynamic conditions imposing the associated complex bathymetry. Among other most important points in mapping benthic habitats from a survey data collection is to confidently interpret properties of surface sediments. The degree of uncertainty of the interpretation determines the reliability of the resulting habitat maps.
The objective of the present study is to test whether the hypothetically natural relationship between the surface sediment distribution and complex bathymetry could be used to improve the quality of surface sediment patches mapping. This is based on our hypothesis that grain-size characteristics of the ridge surface sediments must be intrinsically related to the hydrodynamic condition (storm-induced currents) and the geometry of the seabed morphology. The area features two-parallel shoreface-connected ridges which is situated obliquely WNWSSE oriented and mostly sandy in texture. We made use the median grain-size (d50) as the predictand and the bathymetry as the covariable to produce a high-resolution raster map of median grain-size distribution using the Cokriging interpolation.
The Cokriging method has never been tested before in such a relatively small high-energetic and shallow coastal shelf. Using Cokriging, we interpolated the point map of sparse grab samples of 500 × 500 m grids, and 250 × 250 m grids at a small location nearshore, into 10 × 10 m pixel size full coverage (raster) map. The interpolation results with Cokriging support our prediction that there is a positive relationship between surface grain-size distribution and complex seabed bathymetry in high-energetic coastal shelf. Besides the moderate correlation obtained from the Pearson correlation (r = 0.44), the cross-variogram between the two variables shows a more precise nature of their spatial correlation, which is physically meaningful for the interpolation process. For our relatively small-scale study area, we found KED, the other multivariate geostatistic technique, is rather redundant, while the univariate Anisotropic Kriging creates a smoothing effect, which overlooked the abrupt changes in bathymetry particularly in the direction of the anisotropy. Compared to the results using these methods, the Cokriging interpolation result can capture well the detail of patchiness of surface sediment described in the other study.
For a high-energy and shallow sandy shelf like the Spiekeroog of the German Bight, it is rightly assumed that the surface sediment patches predominantly determine the habitable conditions for the macro-benthic habitat. The future outlook of the present study to investigate whether correlations also exists across different level of habitat structures, and whether under the ever-escalated extreme-climatic driving force the large-scale seabed features such as the shore-connected sand ridges create a sheltered area for fish growth, providing the high-energetic storm-induced current. The present study partially contributes to fill in the gaps in physical information in a high-energetic and shallow coastal shelf.
6. Acknowledgements
We acknowledge the Deutsche ForschungsGemeinschaft (DFG) for financially supporting the study under the framework of Integrated Coastal Zone and Shelf Sea Research (INTERCOAST)—University of Bremen, Germany. We gratefully acknowledge the Senckenberg Institute for Marine Geology at Wilhelmshaven, Germany for the research collaboration and for providing access for the datasets of the Spiekeroog. We thank Dr. Adam Kubicki for furnishing the grab sampling and bathymetry datasets.
REFERENCES
- V. E. Kostylev, “Benthic Habitat Mapping from Seabed Acoustic Surveys: Do Implicit Assumptions Hold?” In: M. Z. Li, C. R. Sherwood and P. R. Hill, Eds., Sediments, Morphology and Sedimentary Processes on Continental Shelves, International Association of Sedimentologists Special Publication, 44(IAS), Wiley-Blackwell, Oxford, 2011.
- C. H. Moore, E. S. Harvey and K. P. van Niel, “Spatial Prediction of Demersal Fish Distributions: Enhancing Our Understanding of Species-Environment Relationships,” ICES Journal of Marine Science, Vol. 66, 2009, pp. 2068-2075. doi:10.1093/icesjms/fsp205
- J. R. Ellis, S. I. Rogers and S. M. Freeman, “Demersal Assemblages in the Irish Sea, St George’s Channel and Bristol Channel,” Estuarine, Coastal and Shelf Science, Vol. 51, 2000, pp. 299-315. doi:10.1006/ecss.2000.0677
- R. A. McConnaughey and K. R. Smith, “Associations between Flatfish Abundance and Surface Sediments in the Eastern Bering Sea,” Canadian Journal of Fisheries and Aquatic Sciences, Vol. 57, No. 12, 2000, pp. 2410- 2419. doi:10.1139/f00-219
- J. Kooij, van der S. Kupschus and B. E. Scott, “Delineating the Habitat of Demersal Fish Assemblages with Acoustic Seabed Technologies,” ICES Journal of Marine Science, Vol. 68, No. 9, 2011, pp. 1973-1985. doi:10.1093/icesjms/fsr124
- E. Verfaillie, V. V. Lancker and M. V. Meirvenne, “Multivariate Geostatistics for the Predictive Modelling of the Surface Sand Distribution in Shelf Seas,” Continental Shelf Research, Vol. 26, 2006, pp. 2454-2468. doi:10.1016/j.csr.2006.07.028
- A. J. Kenny, I. Cato, M. Desprez, Fader, R. T. E. Schüttenhelm and J. Side, “An Overview of Seabed-Mapping Technologies in the Context of Marine Habitat Classification,” ICES Journal of Marine Science, Vol. 60, No. 2, 2003, pp. 411-418. doi:10.1016/S1054-3139(03)00006-7
- J. D. Sisson, J. Shimeta, C. A. Zimmer and P. Traykovski, “Mapping Epibenthic Assemblages and Their Relations to Sedimentary Features in Shallow-Water, High-Energy Environments,” Continental Shelf Research, Vol. 22, No. 4, 2002, pp. 565-583. doi:10.1016/S0278-4343(01)00074-7
- M. Diesing, A. Kubicki, C. Winter and K. Schwarzer, “Decadal Scale Stability of Sorted Bedforms, German Bight, Southeastern North Sea,” Continental Shelf Research, Vol. 26, No. 8, 2006, pp. 902-916. doi:10.1016/j.csr.2006.02.009
- M. Leecaster, “Spatial Analysis of Grain-Size in Santa Monica Bay,” Marine Environmental Research, Vol. 56, No. 1-3, 2003, pp. 67-78. doi:10.1016/S0141-1136(02)00325-2
- E. E. Antia, “Rates and Patterns of Migration of Shoreface-Connected Sandy Rdiges along the Southern North Sea Coast,” Journal of Coastal Research, Vol. 12, No. 1, 1996, pp. 38-46. ISSN: 0749-0208.
- E. E. Antia, “Surface Grain-Size Statistical Parameters of a North Sea Shoreface-Connected Ridge: Patterns and Process Implication,” Geo-Marine Letter, Vol. 13, 1993, pp. 172-181. doi:10.1007/BF01593191
- H. Reiss, S. Degraer, G. C. A. Duineveld, I. Kroencke, J. Aldridge, J. A. Craeymeersch, et al., “Spatial Patterns of Infauna, Epifauna, and Demersal Fish Communitites in the North Sea,” ICES Journal of Marine Science, Vol. 67, No. 2, 2010, pp. 278-293. doi:10.1093/icesjms/fsp253
- A. Lezama-Ochoa, M. Ballon, M. Woillez, D. Grados, X. Irigoien and A. Bertrand, “Spatial Patterns and ScaleDependent Relationships between Macrozooplankton and Fish in the Bay of Biscay: An Acoustic Study,” Marine Ecology Progress Series, Vol. 439, 2011, pp. 151-168. doi:10.3354/meps09318
- F. D. van der Meer, “Introduction to Geostatistics,” ITC Lecture Notes, ITC, Enschede, 1993, p. 72.
- P. Goovaerts, “Geostatistics for Natural Resources Evaluation,” Oxford University Press, New York, 1997.
- D. F. Maune, Ed., “Digital Elevation Model Technologies and Applications: The DEM Users Manual,” ASPRS, Bethesda, 2001.
- H. J. de Knegt, F. van Langevelde, M. B. Coughenour, A. K. Skidmore, W. F. de Boer, I. M. A. Heitkönig, et al., “Spatial Autocorrelation and the Scaling of Species-Environment Relationships,” Ecology, Vol. 91, 2010, pp. 2455- 2465.
- N. Cressie, “Statistics for Spatial Data,” Wiley, New York, 1993.
- H. Wackernagel, “Multivariate Geostatistics,” Springer, London, 2003.
- A. G. Journel and C. J. Huijbregts, “Mining Geostatistics,” Academic Press, New York, 1978.
- H. Wackernagel, “Multivariate Geostatistics,” Springer, Berlin, 1998.
- C. V. Deutsch, and A. G. Journel, “GSLIB: Geostatistical Software Library and User’s Guide,” Oxford University Press, Oxford, 1992.
- S. Dowdy and S. Wearden, “Statistics for Research,” Wiley, New York, 1983.
- E. H. Isaaks and R. M. Srivastava, “An Introduction to Applied Geostatistics,” Oxford University Press, New York, 1989.
- S. F. Thrush, J. E. Hewitt, G. A. Funnell, V. J. Cummings, J. Ellis, D. Schultz, et al., “Fishing Disturbance and Marine Biodiversity: The Role of Habitat Structure in Simple Soft-Sediment Systems,” Marine Ecology Progress Series, Vol. 223, 2001, pp. 277-286. doi:10.3354/meps223277
- A. Genin, “Bio-Physical Coupling in the Formation of Zooplankton and Fish Aggregations over Abrupt Topographies,” Journal of Marine System, Vol. 50, No. 1-2, 2004, pp. 3-20. doi:10.1016/j.jmarsys.2003.10.008
- A. Bertrand, F. Gerlotto, S. Bertrand, M. Gutierrez, et al., “Schooling Behaviour and Environmental Forcing in Relation to Anchoveta Distribution: An Analysis across Multiple Spatial Scales,” Progress in Oceanography, Vol. 79, 2008, pp. 264-277. doi:10.1016/j.pocean.2008.10.018.
NOTES
*Corresponding author.

