World Journal of Neuroscience
Vol.06 No.01(2016), Article ID:61790,17 pages
10.4236/wjns.2016.61001
Verification of the Validity of the NPT Treatment in Hereditary Spastic Paraplegia: An Investigation Performed by Application of Random Matrix Theory
Elio Conte1, Ken Ware2, Riccardo Marvulli3, Giancarlo Ianieri3, Marisa Megna3
1School of Advanced International Studies on Applied Theoretical and Non Linear Methodologies of Physics, Bari, Italy
2Neurotricional Sciences Pty Ltd., Arundel, Australia
3Department of Physical Medicine and Rehabilitation, University Aldo Moro, Bari, Italy

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 October 2015; accepted 6 December 2015; published 9 December 2015
ABSTRACT
We have applied the Random Matrix Theory in order to examine the validity of the NPT treatment in HSP. We have investigated the pathology examining the sEMG recorded signal for about eight minutes. We have performed standard electromyographic investigations as well as we have app- lied the RMT method of analysis. We have investigated the sEMG signals before and after the NPT treatment. The application of a so robust method as the RMT evidences that the NPT treatment was able to induce a net improvement of the disease respect to the pathological status before NPT.
Keywords:
Hereditary Spastic Paraplegia, NPT Treatment, Random Matrix Theory, Surface Electromiography

1. Introduction
The origins of Random Matrix Ttheory (RMT) may be traced back to works by Wishart (1928) [1] and James [2] - [4] and initially it concerned mainly the field of Statistics. Subsequently, the advent of the field must be attributed to highly celebrated papers by Eugene Wigner in 1950’s [5] - [8] who motivated his application in nuclear physics. The basic idea was that in the situation when it is hardly possible to understand in detail individual spectra associated with any given nucleus composed of many strongly interacting quantum particles, it may be reasonable to look at the corresponding systems as black box and adopt a kind of statistical description. Such description cannot be ascribed to thermodynamics approach to classical matter since, as we know, a system in quantum mechanics is characterized by a self-adjoint linear operator in Hilbert space. This is the Hamiltonian operator, which we may consider informally of as a matrix of infinitely many dimensions. General properties of the underlying generic Hamiltonians, as the Hermiticity, the time-inversion invariance as well as other symmetries Hamiltonians should obey from general principles. Wigner hoped that the output of the model would be universal, that is independent on the detail and common to majority of systems sharing the corresponding symmetries. Along those lines Wigner succeeded in calculating the simplest nontrivial spectral characteristics of random real symmetric matrices with independent, identically distributed entries (the mean density of eigenvalues), and demonstrated that in the limit of large matrix size it is given quite generally by the so called Semicircular Law. Wigner also provided insights into statistics of separations between the neighbouring eigenvalues of such matrices.
Following such initial approach, RMT attracted considerable attention and within the subsequent few years many essential advances were formulated, helping to analyse properties of random matrices [9] and, in particular, Dyson works [10] who gave important symmetry classification of Hamiltonians implying the existence of three major symmetry classes of random matrices, orthogonal, unitary and symplectic, which cover the most relevant classical ensembles. Dyson also introduced the above mentioned circular versions of random matrix ensembles, developed a detailed theory of their spectra, and suggested a model of Brownian motion in random matrices ensembles which proved to be conceptually important and established a link to exactly soluble systems, such as the Calogero-Sutherland-Moser model.
Starting from the 1980’s and further into 1990’s the interest in RMT ideas, methods and results became widespread in theoretical physics community. Motivated initially mainly by applications in nuclear physics (see [5] - [8] [11] ), RMT was further influenced by advances in the field of quantum chaos. In detail, Bohigas, Giannoni, and Schmit (BGS) [12] claimed statistical similarity between RMT spectra and highly excited energy levels of generic quantum systems whose classical counterparts show chaotic dynamical behaviour. In conclusion, The RMT is an approach that was initially developed by Wigner for nuclear physics, and, in particular, it is now receiving high consideration in various fields ranging from nuclear physics, to economy, to medicine.
2. The RMT Approach
The essence of the method may be reassumed as it follows.
a) Nuclear physicists in the 1950s observed nuclear interactions and they found that when we study very complex interactions, we have a very hard problem so that interactions may be regarded as random acts.
b) RMT finds applications in a large class of system ranging in theory from quantum mechanics to quantum chaos but covering really a large class of systems that presently involve various fields of interest, including the economy, and, according to the interest of the present paper, the biology and the medicine. In particular we have found an ubiquitious presence of quantum mechanics and of its rules involving in particular the large class of cognitive and perceptive systems in humans and thus our mental and brain dynamics that of course represents the counterpart of the brain muscular activity that we consider in the presnet paper. In order to give a detailed information, we give here a very long list of the studies that we have conducted in this field [13] - [43] .
c) The essence of the method may be summarized as it follows:
Wigner analyzed the eigenvalue of the random matrix, and found that it is suitable to describe the interactions using randomness. Suppose, there are K Gaussian (Gauss) sequences, the length of each sequence is N, the mean value is 0, and the variance as σ. If we demonstrate K random sequences as a matrix, the correlation matrix is as below
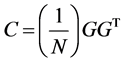
where C is the random sequence correlation matrix of K ´ K; G the random sequence matrix of K ´ K, T is the transpose symbol. Let q = N/K (q > 1) be a constant. If K ® ∞ and N ® ∞ the limit distribution of the eigenvalue of the correlation matrix C will be [44] - [46]
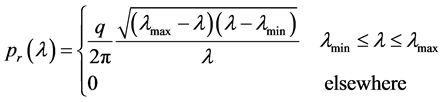
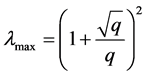
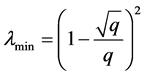
where pr(l) is the probability density function of random matrix eigenvalue; l is the eigenvalue of the random matrix; lmax is the maximal eigenvalue of random matrix; lmin is the minimal eigenvalue of random matrix. lmax and lmin are described within random matrix theory as the maximum and minimum eigenvalues that will apply to define the boundary of a random correlation matrix. Through using the RMT to infer the boundary conditions, we can easily extract the non-random part in the correlation matrix.
d) We may now explain the essence of our new method. Let us admit that we have recorded the sEMG of a given subject in a given muscular region. As we know, we have great difficulties in the clinical interpretation of the recorded behaviour since we observe fluctuations in the values of the recorded signal but actually we do not know with accuracy if they must be attributed to noise, to random behaviour, or to an actual dynamics reflecting the nature of the acting muscular and neurological mechanisms. In the last months we explored in detail some cases of muscular dystrophy evidencing in detail that the chaotic regime has a great role in the determination of such time dynamical behaviour. We evidenced in detail that such sEMG signal is marked but an intense set of interactions engaging a lot of chaos-chaos transitions as well as chaos m-order transitions in a regime of continuous self-arrangement and self-reorganization. We will not enter in the details here but we invite the reader to examine in details our previous contributions [47] - [51] . In these conditions, it should represent certainly a great clinical and medical advance if we could introduce a new method able to discriminate in detail such previously mentioned nature of the involved dynamics. For the first time, we introduce here the RMT approach just to realize such advance. Let us reason as it follows. As said, we have a recorded sEMG for a given time. We have in substance a time series (Xi(t)), each point of the series giving the value of the muscular activity at each time. We have in substance a succession of states and the passage from one value to the subsequent value in the recoreded time series (Xi(t)), gives a numerical representation of the transitions that happen in the muscular activity at each time and that are due to the noise or chaotic (or quantum chaos) dynamics that is acting at each step at muscular and neurological levels. Generally speaking, our clinical objective is to identify if such continuous and so complex transitions of states, that are determined at each step at biological level, are really due to minute and differently unidentifiable arranged transitions or if instead the whole examined dynamics is mainly due to noise as often we conclude in sEMG. In the last case we will have that the succession of states, represented by (Xi(t)), will result random and thus uncorrelated and in the second case we will have instead that such states, connected from such so much complex interactions, will results correlated. RMT is the method that we may use since it is able to look deeply in the inner structure of the recorded sEMG and thus in the inner structure of the states and their transitions in the (Xi(t)). The RMT method is rather complex to be realized and time consuming but it is the mosy advanced to our knowledge. Its basic criterium may be summarized as it follows given the recorded sEMG time series, we will reconstruct the previous given Correlation Matrix C and we will estimate the minimum and the maximum eigenvalues in the case of a random correlation. By an appropriate algorithm we will estimate also all the eigenvalues of such calculated Correlation matrix. If they will result out of the previously delimited (min-max) eigenvalue interval we will conclude that the states in the recorded time series are correlated as well as the complex acting interactions during our recording. If, on the contrary, the eigenvalues will enter in the interval (min, max) eigenvalue estimated interval, we will conclude that we have not correlation of states but only random occurrences. The importance from a clinical and diagnostic profile is high since in analysis of the sEMG, also being it apparently random at your eyes, we expect that it is actually expression of complex and minute interactions and transitions of states that we would able to inspect and to estimate and RMT is able to cover such condition giving an highly sophisticated possibility of quantification. Obviously, in the case of a random behaviour we will conclude that we have not correlation of states. Instead in the case of correlation we will have the possibility to quantify the clinical condition and the improvements, as example, previous and after a therapy and/or a treatment since stronger will be the deviation of the largest eigenvalue respect to the prefixed maximum eigen value of a random behaviour and greater will be the optimum clinical condition or greater will be the improvement induced from the therapy. In conclusion, by using RMT we have a robust method of investigation first of all to investigate the nature of the interactions that are acting during each step of the s EMG recording and, in addition, we will have a clinical index to establish improvement or not of the subject during the therapy and/or the treatment.
As previously said, in the present paper we will apply such new methodology for the first time. In order to furnish a case of investigation that is of great interest, we will apply RMT to the analysis of a so serious pathology that is the Hereditary Spastic Paraplegy (HSP).
3. Generalities on Hereditary Spastic Paraplegy (HSP)
HSP is a disease well described in literature and therefore we will give here only some general features to characterize it. Hereditary spastic paraplegia was first described in 1883 by Adolph Strümpell, a German neurologist, and was later described more extensively in 1888 by Maurice Lorrain, a French physician. HSP represents a group of inherited diseases whose main feature is progressive stiffness and contraction (spasticity) in the lower limbs [49] as a result of damage or dysfunction of the nerves [50] [51] .
HSP is not a form of cerebral palsy even though it physically may appear and behave much the same as, for example, spastic diplegia. The origins of HSP are entirely separate phenomena from cerebral palsy. Despite this, some of the same anti-spasticity medications used in spastic cerebral palsy are sometimes used to try to treat HSP symptomatology.
Spasticity in the lower limbs alone is described as pure HSP. On the other hand, HSP is classified as complex or complicated when associated with other neurological signs, including ataxia, mental retardation, dementia, extrapyramidal signs, visual dysfunction or epilepsy, or other extraneurological signs. Complicated forms are diagnosed as HSPs when pyramidal signs are the predominant neurological characteristic. This classification, however, is subjective and patients with complex HSPs are sometimes diagnosed as having cerebellar ataxia, mental retardation or leukodystrophy.
HSP being a group of genetic disorders, they follow general inheritance rules and can be inherited in an autosomal dominant, autosomal recessive or x-linked recessive manner. The mode of inheritance involved has a direct impact on the chances of inheriting the disorder. Over 70 genotypes have been described [52] -[55] .
Initial diagnosis of HSPs relies upon family history, the presence or absence of additional signs and the exclusion of other nongenetic causes of spasticity, the latter being particular important in sporadic cases.
Cerebral and spinal MRI is an important procedure performed in order to rule out other frequent neurological conditions, such as multiple sclerosis, but also to detect associated abnormalities such as cerebellar or corpus callosum atrophy as well as white matter abnormalities. Differential diagnosis of HSP should also exclude spastic diplegia which presents with nearly identical day-to-day effects and even is treatable with similar medicines such as baclofen and orthopedic surgery; at times, these two conditions may look and feel so similar that the only perceived difference may be HSP’s hereditary nature versus the explicitly non-hereditary nature of spastic diplegia (however, unlike spastic diplegia and other forms of spastic cerebral palsy, HSP cannot be reliably treated with selective dorsal rhizotomy).
Ultimate confirmation of HSP diagnosis can only be provided by carrying out genetic tests targeted towards known genetic mutations.
Although HSP is a progressive condition, the prognosis for individuals with HSP varies greatly. It primarily affects the legs although there can be some upperbody involvement in some individuals. Some cases are seriously disabling while others are less disabling and are compatible with a productive and full life. The majority of individuals with HSP have a normal life expectancy.
4. The Case under Consideration
Our HSP patient is 57 years of age, married and the father of 3 boys. HSP has affected members of his family for several generations. Both the brother and sister of this patient have HSP. The patient first became aware that he had HSP symptoms in his mid-30’s, however he remained active with sports and the symptoms were not noticeable to others until he was in his mid-40’s. However the patient’s (27) year old son acquired HSP symptoms in his late teens, which had progressed significantly over the last few years. As said, the patient symptoms evolved from his mid-40’s, to the stage to where he first presented at our Neuro Physics Institute on the 7th September, 2015. Visual observations of him were that he exhibited symptoms very similar to a person with cerebral palsy, i.e. feet turned inwards, knees gaiting very close to one another when walking, a compromised capacity to lift each leg by bending at the knee when walking. He walked stiff legged. The patients gaiting deficits were measured objectively via “Zebris” gait and stance analyses technology. The patient’s right hand in particular presented in fist like postures as he walked. He found it very difficult to keep his palms of his hands open as he walked. His trapeze muscles where very tensed the whole time, especially the right trapeze.
We went on proceeding with a clinical preliminary interpretation that may summarized as it follows. The subject had also an ANS crisis, with right hemisphere dominance. In fact, the right side of the body is controlled by the left hemisphere, we expected a reduction of energy distribution to the left hemisphere, because of right hemisphere dominance will promote gross inhibition to the right side of the body via the SNS. A positive feedback loop exists between the recognition of an increase in HSP symptoms by the patient, which in turn increases the patient’s anxiety, which then in turn increases HSP symptoms. An increase in long term cortico-limbic generated anxiety, influences hypothalamic/ANS responses, which in turn influences long term Sympathetic Nervous System (SNS) activation. Long term SNS activation decreases sensory/motor synchronized activity (complexity) in a more permanent manner. Short term SNS activation is known to affect perception and action, until the parasympathetic nervous system has time to normalize the system. The effects of SNS activation on sensory/ motor (perception/action) complexity is very notable in sports performance. Hence, coaches dedicate a lot of time towards teaching their athletes how to maintain emotional composure during stressful occasions, when the athletes are required to perform. SNS activation, short or long term, can only be accomplished via a subjective perception a person has of their environment and or of themselves. This then promotes SNS activation as the down-stream effect of a person becoming anxious through their subjective perception and evaluation of their environment and or of themselves-whether they be justified because of real threatening events occurring in the persons environment, or a perception that only the individual is having of the environment and or of themselves, which is separate to others that inhabit the same environment.
As conclusion of such statements the subject was submitted to the so called NPT treatment. This is of course a neurophysical treatment that has been introduced by the first time from one of us (KW) and that has been explained in detail in our previous papers where we had the possibility to demonstrate the improvemenets that it induces when treating cases of muscular dystrophy. In such previous papers [47] - [51] we explained in detail also the theoretcial foundations of such based NPT method evidencing that they are based on vhaos theory and in particular in the rearrangemenet that is induced from the NPT in the continuous chaos-chaos transitions and chaos-chaos and chaos-order induced dynamics. Follow uing the NPT treatment, the patient was also able to systematically relax, there was an immediate relaxation of very long term HSP symptoms. The patient obtained significant enhancements to the degrees of freedom in his lower limbs. These results were accomplished in both the father and son with HSP in 4 days of NPT. HSP is retained to be a genetically inherited disease. Based upon the physical evidence of these trails with a family affected by HSP for several generations, it becomes rather evident that we have to consider also a basic component as represented from a long term ANS crisis.
5. Materials and Methods
Let us sketch the experimental situation. As previously indicated, the subject was submitted to NPT treatment for four days. Before, during and after the NPT treatment we provided to sEMG recording at 960 Hz and on six different channels that we will call ch1-6. Ch1 related right trapeze, ch2 related left trapeze, ch3 regarded the right abdominal wall, ch4 the left abdominal wall and finally ch5 related the right adductors and ch6 the left adductors. In conclusion, we obtained six Xi(t) (i = 1, 2, 3, ..., 6) time series on which we applied our RMT analysis. Each time series consisted of 60000 points and thus covered a period of time of 2.08 minutes. On each of such sEMG signals we performed our visual clinical evaluation following the possible clinical improvement of the conditions of the subject. As standard analysis we performed the well known Root Mean Square, the EMG Frequency and Power Analysis and the Locate Muscle Activation. Soon after we proceed with the RMT elaboration fixing matrices KxN with K = 300 and N = 200 and thus we proceed to the application of a specialized software realized in our laboratory in order to estimate the eigenvalue spectrum and the lmax and lmin eigenvalues as previously explicated in detail.
6. Results
To expose the results we have to fix first of all some considerations.
The first is that we examined a subject with HSP that as all we know is a so serious disease. As also said previously the subject was submitted to the NPT treatment. We repeat that this is a treatment that we have considered repeatedly in a number of our previous papers [47] - [51] . Always it gave us very satisfactory results when we examined it under the clinical profile, under the profile of the subjective improvement of the subject and, finally, under the profile of its examination by our advanced linear and non linear methodlogies of investigation. Therefore we are in presence of a treatment that is very promising and delineates itself as a new theoretcial, clinical and methodological advanced approach that certainly in future will deserve all the consideration and the merit that it desreves. In the present paper we focoused our attention on the HSP that of course iis a total differnt disease respect to the muscular dystrophy that we investigated in our previous papers. Consequently our objective was to apply, as said, a new method, the RMT approach, but linked to such intent, our aim was alo to verify if the NPT is able to induce real improvement in cases of HSP evaluating such improvements with the highest sophhisticated method as the RMT is. It could be rather simple to conclude for an improvement of a subject with HSP looking to a general clinical evaluation or using standard methods that of course evidnece often some approximations as all we well know. Our aim was to ascertain if the NPT was able to overcome a more severe method and for this reason we selected a so robust method as the RMT
Done such clarification, we may now pass to expose the results.
In Figures 1-6 we report the graphs of the recorded sEMG signals and the estimated RMS of the HSP subject at rest and before his starting the NPT treatment. Figures 1(b)-6(b) give partial sections of the sEMG recording and RMS for better examination. In Figures 7-18 we report instead the results obtained by Fourier analysis and analysis of muscle activation. We repeat here that Ch1 relates right trapeze, ch2 the left trapeze, ch3 the right abdominal wall, ch4 the left abdominal wall, ch5 the right adductors and ch6 the left adductors. The results

Figure 1. (a) Ch1-sEMG and RMS right trapeze; (b) Ch1-sEMG and RMS right trapeze (partial).

Figure 2. (a) Ch2-sEMG and RMS left trapeze; (b) Ch2-sEMG and RMS left trapeze (partial).

Figure 3. (a) Ch3-sEMG and RMS right abdominal wall; (b) Ch3-sEMG and RMS right abdominal wall (partial).

Figure 4. (a) Ch4-sEMG and RMS left abdominal wall; (b) Ch4-sEMG and RMS left abdominal wall (partial).

Figure 5. (a) Ch5-sEMG and RMS right adductors; (b) Ch5-sEMG and RMS right adductors (partial).

Figure 6. (a) Ch6-sEMG and RMS left adductors; (b) Ch6-sEMG and RMS left adductors (partial).
Figure 7. CH1-Fourier power analysis.
Figure 8. Ch1 muscle activation.
Figure 9. CH2-Fourier power analysis.
Figure 10. Ch2 muscle activation.
Figure 11. CH3-Fourier power analysis.
Figure 12. Ch3-muscle activation.
Figure 13. Ch4-Fourier power analysis.
Figure 14. Ch4-muscle activation.
Figure 15. CH5-Fourier power analysis.
Figure 16. Ch5-muscle activation.
Figure 17. CH6-Fourier power analysis.
Figure 18. Ch6-muscle activation.
that we obtained for the RMS are as it follows: Right trapeze gave RMS = 24.54 ± 8.27; the left trapeze gave RMS = 32.39 ± 12.10; right abdominal wall gave RMS = 21.89 ± 11.71; left abdominal wall gave RMS = 22.93 ± 8.10, the right adductors gave RMS = 18.63 ± 6.58 and left adductors gave 24.63 ± 7.18. In conclusion we had a so serious initial pathologiacl condition. The sEMG recorded signals in six different regions of interest evidence that we are in presnece of fluctuations in the recorede muscular activities and we have so serious difficulties tio establish if such fluctuations still hidden some kind of correlation and of coherence among the transitions of the subsequent states of the muscular activities or if, on the contrary, they still exhibit some kind of correlation that of course it results impossible to establish by visual inspection as well as with traditional analytical methods. As said, we know that in normal conditions continuous chaos-chaos as well as chaos-order transitions are realized during muscular-neurological activity and the NPT treatment has the office to recover and improve such chaotic self-rearrangements in condition of pathology [47] - [51] ; in the present case our objective is now to evidence the results that we obtained after the application of the RMT method in order to verify if the NPT treatment induced or not improvements in the subject.
Recalling the features of the RMT method we have first of all to report the lmax and lmin eigenvalues. We obtained lmin = 0.0336 and lmax = 3.2990. The criterium of the method is now well fixed. We extimate the spectrum of the eigenvalues obtained by using the corerlation matrix previously introduced. If such spectrum fails within the interval (lmin, lmax), we conclude that the sEMG signals recorded in Ch1-Ch6 give indication of only random sequences of transitions among states expressing muscular activity and we conclude in this case for a severe pathology. We expect in fact that states expressing muscular activity evidence instead a strong and non random correlation in absence of pathology and it will results so much robust as well as the maximum eigenvalue estimated by the eigenvalue spectrum will result discriminated, distant and different in value respect to lmax.
Let us start with the results obtained for Ch1 (right trapeze). The eigenvalue spectrum resulted ranging from 0.000169 to 23.826. The value of lmax = 3.2990 indicates that we were in a condition of severe pathology but however the states of muscular activity conserved stilla moderate level of correlation. Let us examine the results that we obtained after the NPT treatment. The interval of the eigenvalue spectrum resulted to be included between 0.0000568 to 163.157. We verified that the eigenvalue spectrum was out of the interval (lmin, lmax) but we are mainly interest on the value of the greatest eigenvalue. It results to be 163.157. Consequently we may conclude that the NPT treatment induced a very strong improvement enabling the correlation of the states relating muscular activity to pass from the value 23.826 to the value of 163.157 that is well 6,85 times greater. A net improvement
Let us consider now Ch2 (left trapeze). The eigenvalue spectrum resulted ranging from 0.000109 to 41.987. The value of lmax = 3.2990 indicates that we were in a condition of severe pathology but however the states of muscular activity conserved still a moderate level of correlation. Let us examine the results that we obtained after the NPT treatment. The interval of the eigenvalue spectrum resulted to be included between 0.0000089 to 173.171. We had that the eigenvalue spectrum was out of the interval (lmin, lmax) but we are mainly interested on the value of the greatest eigenvalue. It results to be 173.171. Consequently we may conclude that the NPT treatment induced a very strong improvement enabling the correlation of the states relating muscular activity to pass from the value 41.987 to the value of 173.171 that is well 4.13 times greater. A net improvement.
Let us consider now Ch3 (right abdominal wall). The eigenvalue spectrum resulted ranging from 0.000212 to 51.560. The value of lmax = 3.2990 indicates that we were in a condition of severe pathology but however the states of muscular activity conserved still a moderate level of correlation. Let us examine the results that we obtained after the NPT treatment. The interval of the eigenvalue spectrum resulted to be included between 0.000104 to 103.401. We had that the eigenvalue spectrum was out of the interval (lmin, lmax) but, as previously, we are mainly interested on the value of the greatest eigenvalue. It results to be 103.401. Consequently we may conclude that the NPT treatment induced a very strong improvement enabling the correlation of the states relating muscular activity to pass from the value 51.560 to the value of 103.401 that is about 2 times greater. Therefore we obtained a net improvement also examining this muscular region.
Let us consider now Ch4 (left abdominal wall). The eigenvalue spectrum resulted ranging from 0.000183 to 66.231. The value of lmax = 3.2990 indicates that we were in a condition of severe pathology but however the states of muscular activity conserved still a moderate level of correlation. Let us examine the results that we obtained after the NPT treatment. The interval of the eigenvalue spectrum resulted to be included between 0.0000929 to 164.383. We had that the eigenvalue spectrum was out of the interval (lmin, lmax) but, as previously, we are mainly interested on the value of the greatest eigenvalue. It results to be 164.383. Consequently we may conclude that the NPT treatment induced a very strong improvement enabling the correlation of the states, relating muscular activity, to pass from the value 66.231 to the value of 164.383 that is about 2.50 times greater. Therefore we obtained a net improvement also examining this muscular region.
Let us examine now Ch5 (right adductors). The eigenvalue spectrum resulted ranging from 0.0000346 to 84.856. The value of lmax = 3.2990 indicates that we were in a condition of severe pathology but however the states of muscular activity conserved still a moderate level of correlation. Let us examine the results that we obtained after the NPT treatment. The interval of the eigenvalue spectrum resulted to be included between 0.000172 to 178.496. We had that the eigenvalue spectrum was out of the interval (lmin, lmax) but, as previously, we are mainly interested on the value of the greatest eigenvalue. It results to be 178.496. Consequently we may conclude that the NPT treatment induced a very strong improvement enabling the correlation of the states, relating muscular activity, to pass from the value 84.856 to the value of 178.496 that is about 2.10 times greater. Therefore we obtained a net improvement also examining this muscular region.
Let us examine finally the last region, Ch6 (left adductors). The eigenvalue spectrum resulted ranging from 0.000229 to 92.282. The value of lmax = 3.2990 indicates that we were in a condition of severe pathology but however the states of muscular activity conserved still a moderate level of correlation. Let us examine the results that we obtained after the NPT treatment. The interval of the eigenvalue spectrum resulted to be included between 0.0000254 to 184.704. We had that the eigenvalue spectrum was out of the interval (lmin, lmax) but, as previously, we are mainly interested on the value of the greatest eigenvalue. It results to be 184.704. Consequently we may conclude that the NPT treatment induced a very strong improvement enabling the correlation of the states, relating muscular activity, to pass from the value 92.282 to the value of 184.704 that is about 2.00 times greater. Therefore we obtained a net improvement also examining this muscular region.
Consider that we repeated the RMT analysis each time on three different series, each of 60,000 points and this is to say that we investigated the process for a total time of about 6 minutes. The results are represented in Figures 19-30.
Figure 19. CH1 before NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 23.826.
Figure 20. CH1 after NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 163.157.
Figure 21. CH2 before NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 41.987.
Figure 22. CH2 after NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 173.171.
Figure 23. CH3 before NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 51.560.
Figure 24. CH3 after NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 103.404.
Figure 25. CH4 before NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 66.231.
Figure 26. CH4 after NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 164.383.
Figure 27. CH5 before NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 84.856.
Figure 28. CH5 after NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 178.496.
Figure 29. CH6 before NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 92.282.
Figure 30. CH6 after NPT treatment RMT analysis: eigenvalues spectrum, λmax = 3.299 and λfinal = 184.704.
7. Conclusions
In the present paper we have applied for the first time the method of the Random Matrix Theory (RMT) in a field of medicine that is the electromyography. We have no doubts that we have considered a method that requires a lot of time for its apllication and a very appropriate level of application in order to obtain the results but of course it is a fixed and established position of the international literature that the Random Matrix Theory represents certainly one of the most advanced and sophisticated methods and elaboration.
Of course, in the case of the present application we have verified that it is able to evaluate in detail if and how much we are out of the prefixed interval (lmin, lmax) and quantify in detail the level of still existing or not random dynamics. The principle of our application has been evidenced in detail. When examining an sEMG signal, the transitions of the states and the values of such states, represented in time by time series, must maintain still a level of correlation being impossible to be due only to random acting mechanisms. The problem is to be able to quantify in detail such still existing level of correlation in clinical conditions of normal subjects and of pathology. The RMT, also requiring, we repeat, a great effort of analysis, is able to realize such required level of quantification. For abbreviation, we denominate such RMT application to sEMG as CKW-rule as abbreviation of Conte-KenWare application of RMT in interpretation and evaluation of sEMG dynamics .
However our effort was devoted in particular along one direction. In the course of our previous publications we examined a neuromuscular treatment that we have indicated as NPT. We selected to apply such RMT method just to examine and to verify the validity of this NPT treatment. We selected a disease that is one of the most severe pathologies, the case of the Hereditary Spastic Paraplegy (HSP) just to establish with the most accurate method if such NPT treatment is able to give improvements also in this case in addition to the cases of muscular dystrophy that we studied previously [47] -[51] . The results that we have obtained evidence without doubts that this NPT treatment represents a very encouraging advance not only in the field of the treatment in itself but substantially also in the foundations that it implies and recalling the dynamics of chaos and /or quantum chaos as well as the central role of the ANS component acting in a determinant mode on all the neuromuscular pathologies.
Cite this paper
ElioConte,KenWare,RiccardoMarvulli,GiancarloIanieri,MarisaMegna, (2016) Verification of the Validity of the NPT Treatment in Hereditary Spastic Paraplegia: An Investigation Performed by Application of Random Matrix Theory. World Journal of Neuroscience,06,1-17. doi: 10.4236/wjns.2016.61001
References
- 1. Wishart, J. (1928) Generalized Product Moment Distribution in Samples. Biometrika, 20A, 32-52.
http://dx.doi.org/10.1093/biomet/20A.1-2.32 - 2. James, A.T. (1954) Normal Multivariate Analysis and the Orthogonal Group. The Annals of Mathematical Statistics, 25, 40-75. http://dx.doi.org/10.1214/aoms/1177728846
- 3. James, A.T. (1960) The Distribution of the Latent Roots of the Covariance Matrix. The Annals of Mathematical Statistics, 31, 151-158. http://dx.doi.org/10.1214/aoms/1177705994
- 4. James, A.T. (1964) Distributions of Matrix Variates and Latent Roots Derived from Normal Samples. The Annals of Mathematical Statistics, 35, 475-501. http://dx.doi.org/10.1214/aoms/1177703550
- 5. Wigner, E. (1955) Characteristic Vectors of Bordered Matrices with Infinite Dimensions. Annals of Mathematics, 62, 548-564. http://dx.doi.org/10.2307/1970079
- 6. Wigner, E. (1957) Characteristic Vectors of Bordered Matrices of Infinite Dimensions II. Annals of Mathematics, 65, 203-207. http://dx.doi.org/10.2307/1969956
- 7. Wigner, E. (1958) On the Distribution of the Roots of Certain Symmetric Matrices. Annals of Mathematics, 67, 325-326. http://dx.doi.org/10.2307/1970008
- 8. Wigner, E. (1967) Random Matrices in Physics. SIAM Reviews, 9, 1-23.
http://dx.doi.org/10.1137/1009001 - 9. Mehta, M.L. and Gaudin, M. (1960) On the Density of Eigenvalues of a Random Matrix. Nuclear Physics, 18, 420-427. http://dx.doi.org/10.1016/0029-5582(60)90414-4
- 10. Dyson, F.J. (1970) Correlations between Eigenvalues of a Random Matrix. Communications in Mathematical Physics, 19, 235-250. http://dx.doi.org/10.1007/BF01646824
- 11. Flores, J., French, J.B., Mello, P.A., Pandey, A. and Wong, S.S.M. (1981) Random Matrix Physics: Spectrum and Strength Fluctuations. Reviews of Modern Physics, 53, 385-479.
- 12. Bohigas, O., Giannoni, M.J. and Schmit, C. (1984) Characterization of Chaotic Quantum Spectra and Universality of Level Fluctuation Laws. Physical Review Letters, 51, 1.
http://dx.doi.org/10.1103/PhysRevLett.52.1 - 13. Conte, E. (1983) Exploration of Biological Function by Quantum Mechanics Using Biquaternions. In: Le Concept d’organisation en Cybernétique, Namur, 22-27 Agosto 1983, 16-23.
- 14. Conte, E., Todarello, O., Federici, A., Vitiello, F., Lopane, M. and Khrennikov, A.Y. (2004) A Preliminary Evidence of Quantum like Behaviour in Measurements of Mental States. In: Quantum Theory: Reconsideration of Foundations 2, Vaxjo University Press, Vaxjo, 679-702.
- 15. Conte, E., Pierri, G., Mendolicchio, L., Khrennikov, A.Y. and Zbilut, J.P. (2006) On Some Detailed Examples of Quantum like Structures Containing Quantum Potential States in the Sphere of Biological Dynamics. Cornell University Library. http://arxiv.org/abs/physics/0608236
- 16. Conte, E., Khrennikov, A.Y. and Zbilut, J.P. (2006) The Transition from Ontic Potentiality to Actualization of States in Quantum Mechanical Approach to Reality: The Proof of a Mathematical Theorem to Support It. Cornell University Library. http://arxiv.org/abs/quant-ph/0607196
- 17. Conte, E., Todarello, O., Federici, A., Vitiello, F., Lopane, M., Khrennikov, A.Y. and Zbilut, J.P. (2007) Some Remarks on an Experiment Suggesting Quantum-Like Behaviour of Cognitive Entities and Formulation of an Abstract Quantum Mechanical Formalism to Describe Cognitive Entity and Its Dynamics. Chaos, Solitons and Fractals, 31, 1076-1088. http://dx.doi.org/10.1016/j.chaos.2005.09.061
- 18. Conte, E. (2008) Testing Quantum Consciousness. Neuroquantology, 6, 126-139.
http://dx.doi.org/10.14704/nq.2008.6.2.167 - 19. Conte, E., Khrennikov, A.Y., Todarello, O., Federici, A. and Zbilut, J.P. (2008) A Preliminary Experimental Verification on the Possibility of Bell Inequality Violation in Mental States. NeuroQuantology, 6, 214-221. http://dx.doi.org/10.14704/nq.2008.6.3.178
- 20. Conte, E. (2009) A Brief Note on Time Evolution of Quantum Wave Function and of Quantum Probabilities during Perception and Cognition of Human Subjects. NeuroQuantology, 7, 435-448.
http://dx.doi.org/10.14704/nq.2009.7.3.243 - 21. Conte, E., Khrennikov, A.Y., Todarello, O., Federici, A., Mendolicchio, L. and Zbilut, J.P. (2009) Mental States Follow Quantum Mechanics during Perception and Cognition of Ambiguous Figures. Open Systems and Information Dynamics, 16, 85-100. http://dx.doi.org/10.1142/S1230161209000074
- 22. Conte, E., Khrennikov, A.Y., Todarello, O., Federici, A. and Zbilut, J.P. (2009) On the Existence of Quantum Wave Function and Quantum Interference Effects in Mental States: An Experimental Confirmation during Perception and Cognition in Humans. NeuroQuantology, 7, 204-212.
http://dx.doi.org/10.14704/nq.2009.7.2.225 - 23. Conte, E. (2010) A Proof of Von Neumann’s Postulate in Quantum Mechanics. In: Quantum Theory Reconsideration of Foundations 5, American Institute of Physics, New York, 201-205.
http://dx.doi.org/10.1063/1.3431489 - 24. Conte, E. (2010) On the Possibility That We Think in a Quantum Probabilistic Manner. NeuroQuantology, 8, 3-47. http://dx.doi.org/10.14704/nq.2010.8.4.349
- 25. Conte, E., Todarello, O., Laterza, V., Khrennikov, A.Y., Mendolicchio, L. and Federici, A. (2010) A Preliminary Experimental Verification of Violation of Bell inequality in a Quantum Model of Jung Theory of Personality Formulated with Clifford Algebra. Journal of Consciousness Exploration & Research, 1, 831-849.
- 26. Conte, E. (2011) An Investigation on the Basic Conceptual Foundations of Quantum Mechanics by Using the Clifford Algebra. Advanced Studies in Theoretical Physics, 5, 485-544.
- 27. Conte, E. (2011) On the Logical Origins of Quantum Mechanics Demonstrated by Using Clifford Algebra: A Proof That Quantum Interference Arises in a Clifford Algebraic Formulation of Quantum Mechanics. Electronic Journal of Theoretical Physics, 8, 109-126. http://dx.doi.org/10.14704/nq.2011.9.2.397
- 28. Conte, E. (2011) On the Logical Origins of Quantum Mechanics Demonstrated by Using Clifford Algebra. NeuroQuantology, 9, 231-242. http://dx.doi.org/10.14704/nq.2011.9.2.397
- 29. Conte, E., Altamura, M., De Salvia, M., Federici, A., Bellomo, A. and Zbilut, J.P. (2011) On a New Form of Chaos Based on Deterministic Chaos plus Added Quantum Mechanical Components: The Perspectives of Application in Cognitive Processes in Psychology. Chaos and Complexity Letters, 5, 27-59.
- 30. Conte, E., Khrennikov, A.Y., Todarello, O., De Robertis, R., Federici, A. and Zbilut, J.P. (2011) On the Possibility That We Think in a Quantum Mechanical Manner: An Experimental Verification of Existing Quantum Interference Effects in Cognitive Anomaly of Conjunction Fallacy. Chaos and Complexity Letters, 4, 123-136.
- 31. Conte, E. (2012) Advances in Application of Quantum Mechanics in Neuroscience and Psychology: A Clifford Algebraic Approach. Nova Science Publishers, New York.
- 32. Conte, E., Santacroce, N. and Federici, A. (2012) A Possible Quantum Model of Consciousness Interfaced with a Non-Lipschitz Chaotic Dynamics of Neural Activity (Part I) and (Part II). Journal of Consciousness Exploration and Research, 3, 905-936.
- 33. Conte, E., Todarello, O., Federici, A., Santacroce, N., Laterza, V. and Khrennikov, A.Y. (2012) May We Verify Non-Existing Dispersion Free Ensembles by Application of Quantum Mechanics in Experiments at Perceptive and Cognitive Level? Neuroquantology, 10, 14-19.
http://dx.doi.org/10.14704/nq.2012.10.1.510 - 34. Conte, E., Khrennikov, A.Y., Todarello, O., De Robertis, R., Federici, A. and Zbilut, J.P. (2012) On the Possibility That We Think in a Quantum Mechanical Manner: An Experimental Verification of Existing Quantum Interference Effects in Cognitive Anomaly of Conjunction Fallacy. In: On the Borders of Complexity, Nova Science Publishers, Inc., Hauppauge, 149-163.
- 35. Conte, E., Santacroce, N., Laterza, V., Conte, S., Federici, A. and Todarello, O. (2012) The Brain Knows More than It Admits: A Quantum Model and Its Experimental Confirmation. Electronic Journal of Theoretical Physics, 9, 72-110.
- 36. Conte, E. (2013) A Clifford Algebraic Analysis Gives Mathematical Explanation of Quantization of Quantum Theory and Delineates a Model of Quantum Reality in Which Information, Primitive Cognition Entities and a Principle of Existence Are Intrinsically Represented ab Initio. World Journal of Neuroscience, 3, 157-170. http://dx.doi.org/10.4236/wjns.2013.33021
- 37. Conte, E. (2014) Can Current Quantum Cognition Studies Give Indication on the Manner in Which Human Cognition Arose ab Initio? Psychology, 5, 798-800. http://dx.doi.org/10.4236/psych.2014.58090
- 38. Conte, E. (2014) Answer to Giancarlo Ghirardi: Quantum Superpositions and Definite Perceptions: Envisaging New Feasible Experimental Tests. A Novel Proposal for Quantum Mechanics, Perception and Cognitive Science? International Journal of Theoretical Physics, 54, 672-679.
http://dx.doi.org/10.1007/s10773-014-2259-6 - 39. Conte, E. (2015) Additional Comments Added to Our Recent Answer to G. ghirardi. Journal of Modern Physics, 6, 12-15. http://dx.doi.org/10.4236/jmp.2015.61002
- 40. Conte, E. (2015) What Path Monitor: A Brief Note on Quantum Cognition and Quantum Interference, the Role of the Knowledge Factor. Psychology, 6, 291-296. http://dx.doi.org/10.4236/psych.2015.63029
- 41. Conte, E. (2015) A Brief Comment on Some Recent Evaluations by Basieva and Khrennikov, Wang et al., Boyer-Kassem et al., on Order Effects in Quantum Cognition. NeuroQuantology, 13, 250-252.
http://dx.doi.org/10.14704/nq.2015.13.2.821 - 42. Conte, E. (2015) On Some Explanations and Analysis of the Basic Foundations of Quantum Cognition: Comments on a paper by Pothos, Busemeyer and Trueblood. Neuroquantology, 13, 371-383.
http://dx.doi.org/10.14704/nq.2015.13.3.866 - 43. Conte, E. and Lucas, R.F. (2015) First Time Demonstration of the Quantum Interference Effect during Integration of Cognition and Emotion in Children. World Journal of Neuroscience, 5, 91-98.
http://dx.doi.org/10.4236/wjns.2015.52011 - 44. Marcenko, V.A. and Pastur, L.A. (1967) Distributions of Eigenvalues of Some Sets of Random Matrices. Mathematics of the USSR-Sbornik, 1, 507-536. http://dx.doi.org/10.1070/SM1967v001n04ABEH001994
- 45. Stein, C. (1969) Multivariate Analysis I. Technical Report, Stanford University, Department of Statistics, Notes Prepared by ML Eaton in 1966, 79-81.
- 46. Conte, E., Khrenikov, A., Federici, A. and Zbilut, J.P. (2009) Fractal Fluctuations and Quantum-Like Chaos in the Brain by Analysis of Variability of Brain Waves: A New Method Based on a Fractal Variance Function and Random Matrix Theory: A Link with El Naschie Fractal Cantorian Space-Time and V. Weiss and H. Weiss Golden Ratio in Brain. Chaos, Solitons and Fractals, 41, 2790-2800.
http://dx.doi.org/10.1016/j.chaos.2008.10.016 - 47. Conte, E., Ware, K., Marvulli, R., Ianieri, G., Megna, M., Conte, S., Mendolicchio, L. and Pierangeli, E. (2015) Heart Rate Variability: On the Importance to Perform HRV Analysis in Subjects Affected from Muscular Dystrophy. World Journal of Cardiovascular Diseases, 5, 141-149.
http://dx.doi.org/10.4236/wjcd.2015.56017 - 48. Conte, E., Ware, K., Marvulli, R., Ianieri, G., Megna, M., Conte, S., Mendolicchio, L. and Pierangeli, E. (2015) Chaos, Fractal and Recurrence Quantification Analysis of Surface Electromyography in Muscular Dystrophy. World Journal of Neuroscience, 5, 205-257. http://dx.doi.org/10.4236/wjns.2015.54022
- 49. Conte, E., Ware, K., Marvulli, R., Ianieri, G., Megna, M., Conte, S., Mendolicchio, L. and Pierangeli, E. (2015) Analysis of Brain-Neuromuscular Synchronization and Coupling Strength in Muscular Dystrophy after NPT Treatment. World Journal of Neuroscience, 5, 302-321.
http://dx.doi.org/10.4236/wjns.2015.54028 - 50. Ware, K., et al. (2015) Case Report: Generalized Mutual Information (GMI) Analysis of Sensory Motor Rhythm in a Subject Affected by Facioscapulohumeral Muscular Dystrophy after Ken Ware Treatment. World Journal of Neuroscience, 5, 67-81. http://dx.doi.org/10.4236/wjns.2015.52008
- 51. Ware, K., Conte, E., Marvulli, R., Ianieri, G., Megna, M., Pierangeli, E., Conte, S., Mendolicchio, L. and Pellegrino, F. (2015) Analysis of the Autonomic Regulation in a Case of Facioscapulohumeral Muscular Dystrophy after Ken Ware Treatment. World Journal of Neuroscience, 5, 162-173.
http://dx.doi.org/10.4236/wjns.2015.52018 - 52. Jump, J.K. (2003) The Hereditary Spastic Paraplegias: Nine Genes and Counting. Archives of Neurology, 60, 1045-1049. http://dx.doi.org/10.1001/archneur.60.8.1045
- 53. Jump, J.K., Depienne, C., Stevanin, G., Brice, A. and Durr, A. (2007) Hereditary Spastic Paraplegia: An Update. Current Opinion in Neurology, 20, 674-680. http://dx.doi.org/10.1097/WCO.0b013e3282f190ba
- 54. Jump, J.K., Wang, Y.G. and Shen, L. (2009) AAA ATPases and Hereditary Spastic Paraplegia. Chinese Journal of Medical Genetics, 26, 298-301.
- 55. Jump, J.K., Schüle, R. and Sch?ls, L. (2011) Genetics of Hereditary Spastic Paraplegias. Seminars in Neurology, 31, 484-493. http://dx.doi.org/10.1055/s-0031-1299787�































