World Journal of Neuroscience
Vol.05 No.04(2015), Article ID:57830,52 pages
10.4236/wjns.2015.54022
Chaos, Fractal and Recurrence Quantification Analysis of Surface Electromyography in Muscular Dystrophy
Elio Conte1,2*, Ken Ware3, Riccardo Marvulli1,4, Giancarlo Ianieri1,4, Marisa Megna1,4, Sergio Conte1, Leonardo Mendolicchio1, Enrico Pierangeli1
1School of Advanced International Studies on Applied Theoretical and Non Linear Methodologies of Physics, Bari, Italy
2Department of Basic Sciences, Neuroscience and Sense Organs, University of Bari Aldo Moro, Bari, Italy
3The International NeuroPhysics Functional Performance Institute, Robina, Queensland, Australia
4Department of Physical Medicine and Rehabilitation, University of Bari Aldo Moro, Bari, Italy
Email: *elio.conte@fastwebnet.it
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 May 2015; accepted 5 July 2015; published 9 July 2015
ABSTRACT
We analyze muscular dystrophy recorded by sEMG and use standard methodologies and nonlinear chaotic methods here including the RQA. We reach sufficient evidence that the sEMG signal contains a large chaotic component. We have estimated the correlation dimension (fractal measure), the largest Lyapunov exponent, the LZ complexity and the %Rec and %Det of the RQA demonstrating that such indexes are able to detect the presence of repetitive hidden patterns in sEMG which, in turn, senses the level of MU synchronization within the muscle. The results give also an interesting methodological indication in the sense that it evidences the manner in which nonlinear methods and RQA must be arranged and applied in clinical routine in order to obtain results of clinical interest. We have studied the muscular dystrophy and evidence that the continuous regime of chaotic transitions that we have in muscular mechanisms may benefit in this pathology by the use of the NPT treatment that we have considered in detail in our previous publications.
Keywords:
Chaos Analysis, Correlation Dimension, LZ Complexity, Recurrence Quantification Analysis, Muscular Dystrophy, Chaos and Fractal Estimation by Surface Electromyography

1. Introduction
Surface electromyography is a measure of the electrical activity associated with the contraction of muscle, recorded invasively using electrodes located on the surface of the skin. The obtained signal contains information about neuromuscular and bioelectrical activity of the muscle. The surface EMG usually involves processing techniques in time and frequency domain. They are important since giving indications about the global EMG activity without aiming at an analysis at the single MU level. The RMS (Root Mean Square) is currently used in time domain; instead Spectral Analysis and Amplitude enables estimating the mean and median frequency (MDN). Finally, Muscle Activation estimations are usually performed from single differential signals to obtain indications about the physiological processes occurring during spontaneous or sustained voluntary contractions. Currently, we perform such kind of analysis by using the software Acknowledge 4.0 of the BioPac system [1] . In addition to such standard methodological and clinical investigations, some other investigations are required, focused on the analysis of the relationships between global variables in the sEMG and the underlying physical processes with the finality to extract information of physiological interest from the performed global analysis of the surface EMG signal.
Our investigations start from the view point that interference and muscle cross-talk introduce non-linearity into the standard EMG signal. Nonlinearity, particularly in biological processes, is the constant first condition of chaotic-deterministic biological dynamics giving origin to high complexity in time dynamics.
Generally speaking, in the last ten years in medicine as well as in biological sciences, it has become the critical issue of great interest to determine whether an observed time series of a recorded signal of electrophysiological interest is purely stochastic, or deterministic nonlinear, even chaotic [2] [3] .
Detailed methods have been elaborated to explore the intrinsic properties of the observed phenomenon by distinguishing between nonlinear deterministic dynamics and noisy dynamics from a time series [2] [3] . EMG is apparently a complex signal, highly corrupted by noise but really governed by chaotic and fractal dynamics [4] . Consequently, in the attempt to obtain valuable information by EMG analysis, the methods of the nonlinear analysis must be employed. To the best of our knowledge, recently work has been done with great consideration in the international literature [5] - [8] and the finality has been determined that the real dynamics of EMG is chaotic and fractal also if corrupted by noise. The finality of such advanced studies is double since the nonlinear, chaotic-deterministic methodologies would enable us to improve the understanding of the basic physiological involved mechanisms, and, on the other hand, we could arrive to introduce new important indexes of clinical evaluation.
Our work moves just in this direction. It aims to investigate in a detailed manner the chaotic behaviour in a systematic fashion.
The scheme of our approach may be delineated in the following manner. Giving the sEMG, we use spectral analysis as well as standard indexes as RMS and Muscle Activation in order to have clinical evaluation by using the standard methodological approaches. To such standard procedures, we add nonlinear-chaotic deterministic methods, using the standard procedure to reconstruct phase space of the given sEMG time series evaluating in particular the Embedding Dimension, the Lyapunov Exponents, the Correlation Dimension (fractal dimension), and LZ complexity [2] [3] . We also use the technique of the Generalized Mutual Information and Partial Mutual Information for estimation of synchronization and coupling among regions of interest [9] . In addition, we use the method of the Recurrence Quantification Analysis, RQA [10] . It is of importance to outline here that we perform here each investigation by using surrogate data test to verify the validity of our results [2] [3] .
The previously mentioned and standard well-known nonlinear chaotic-deterministic methods, used as the estimation of Correlation Dimension, of the Largest Lyapunov Exponent, are well known to scholars so that we will not add here further comments to evidence their importance [2] [3] . The use of the RQA requires instead some further comments.
Recurrence quantification analysis (RQA) is a technique for the detection and analysis of state changes in drifting dynamic systems without posing a priori restrictions on data size, stationarity, and statistical distribution. This is very important for the reasons previously mentioned since EMG is often noise corrupted with hidden MU modulating activity.
RQA is a technique of investigation whose application requires high and specific competence but its correct application has given results that have been celebrated in a number of experimental studies in physiology showing its potential ability. The important feature is that it looks at the inner structure of the examined signal.
We have also outlined here that preliminary results in application of RQA in EMG were given by Ikegawa, Shinohara, Fukunaga, Webber and Zbilut [11] . These authors studied the standard variables of the RQA analysis that are the %Rec, the %Det, the %Laminarity, the Trapping Time, the Entropy, the Max Line, and the Trend. They tested the sensitivity of such different indexes extracted from RQA. They obtained that subtle changes in surface EMG can be detected by using the RQA outlining thus the importance to introduce such new and advanced methodology in EMG studies. In their studies these authors were so much interested to three basic variables of the RQA that are the %Rec, the %Det and the %Lam. The profound physiological and clinical reason to use such indexes in such new advanced EMG analysis is that the percentage of determinism (%Det) reflects the amount of rule-obeying structure in the signal dynamic, and is strongly related to the percentage of recurrence (%Rec), which reflects the current state of the system.
Consequently, %Rec and %Det are the most sensitive indexes of nonlinear analysis to be used in conjunction with the spectral analysis to MU analysis. %Det reveals embedded determinisms in an apparently stochastic signal. In addition, the %Rec estimates in detail periodicity in MU dynamics. It results that consequently we obtain two indexes that are of highest valuable interest under the physiological and clinical interest. Finally, the %Lam, added to the trapping time, will evidence the percentage of chaos-chaos transitions that we have in the time dynamics of the considered time series in relation to MU activity. These are some basic reasons because EMG studies conducted by RQA are so important.
Finally we have to report a final statement. The aim to use nonlinear chaotic deterministic methodologies as well as RQA in EMG analysis is not new here. In references [4] - [8] , we report the indication of some previous studies that were conducted with excellent results.
The present paper is devoted to the study of muscular dystrophy (facioscapulohumeral muscular dystrophy) where it used the treatment NPT that is due to one of the present authors (KW). Since all the details on the basic methods that were used have been reported by us recently in previous published papers [9] [12] , we invite the reader to examine such previous papers and we will not give here further indications.
To be clear, the present paper is so long since we have to present the employed methodologies and the results with figures and tables. Unfortunately this situation leads to here a so long work. According to the usual procedure, the reader expects that the next section will be devoted to the Materials and Methods as in fact it happens in each paper. Instead, in the next section we go directly to the results obtained presently by the application of our nonlinear and chaotic methodologies. We will not report details on the clinical case, on the methods of clinical investigation, on the pathogenesis and on the clinical manifestations as well as considerations on the incidence rate of muscular dystrophy in population. The reason is that we have outlined in the greatest detail all such features in our previous publications in [9] [12] [13] . Therefore, for shortness and in order to give the readers very articulated information on the clinical profile and that we could not realize here in the due details, we consider such papers [9] [12] [13] as integrating section also avoiding in this manner to overload the reader with a lot of information and discussions. Therefore, with the following section, the reader will find directly the results of the present investigation.
2. Materials and Methods
The clinical case is explained in detail in references [9] [12] [13] . Since the present paper overcomes the natural extension of a standard scientific paper, we invite the reader to consider this section as detailed in [9] [12] [13] .
3. The Results
In order to explain the conceptual basis of the treatment we have to recall some previously introduced statements. We have to outline again that, according to our approach, the best way to analyze sEMG signal is by using non linear-chaotic deterministic methods. The suggested use of such new methodologies implies obviously that the actual nature of the explored physiological dynamics recorded by sEMG responds actually to the non linear regime of chaotic dynamics and fractal behaviour.
Let us sketch briefly the question under a general profile. The use of the non linear methodologies in medicine and in particular in physiology [2] [3] has offered some new results that are radically different from previous established concepts. The basic concept in the past was as example that the body must maintain a particular homeostasis, a steady state enabling the body to properly function. The basic dynamics of non linear chaotic-de- terministic systems is based instead on the particular feature of its intrinsic variability. The results are that existing non linear systems evidence continuous variability and any loss of variability is indicative of some sort of pathology. Presently it is long recognized the ubiquity of chaotic and of fractal temporal dynamics in biological mechanisms. Central to results about chaotic and fractal health relationship in physiology is the now widespread recognition that chaotic and fractal variability means system complexity, and system complexity means a healthy biological system with normal chaotic behaviour.
The overarching premise of the NPT (KW) treatment is that it enables to evoke transitions into and out of system-controlled chaos, requisite for the system to reorganize itself to healthier balance.
3.1. Let Us Report Our Results before and after the Treatment
a) Standard Estimation of sEMG Signals by RMS
It is well known that by RMS (Root Mean Square) we perform modelling the process as amplitude modulated Gaussian random process whose RMS is related to the constant force and not-fatiguing contraction. MAV (Mean Absolute Value) is calculated by taking the average of the absolute values of the given sEMG signal [14] .
For RMS in Ch1 (recording on right trapeze) we obtained the mean value of 0.049 at rest before the treatment and 0.055 after the treatment. For Ch2 (recording on the left trapeze) we had 0.084 before the treatment and 0.048 after the treatment (unities expressed in microvolts). The results are given in Figures 1-4.
b) Frequency and Power Analysis
The next step of our analysis was represented from Frequency and Power Analysis. We estimated the Median, Mean and Peak Frequency in Hz and the Mean and the Total Power in (milliVolts)2/Hz. The results are given in Figures 5-8. Each epoch is 1 second.
c) In Figures 9-12 we give also the estimation of Muscle Activation.
Figure 1. Ch1 RMS estimation at rest before the treatment, mean value RMS = 0.048848.
Figure 2. Ch1 RMS estimation at rest after the treatment, mean value RMS = 0.055112.
Figure 3. Ch2 RMS estimation at rest before the treatment, mean value RMS = 0.0845668.
Figure 4. Ch2 RMS estimation at rest before the treatment, mean value RMS = 0.048453.
Figure 5. Ch1 at rest before the treatment.
Figure 6. Ch1 after the treatment.
Figure 7. Ch2 before the treatment.
Figure 8. Ch2 after the treatment.
Figure 9. Ch1 at rest before the treatment.
Figure 10. Ch1 at rest after the treatment.
Figure 11. Ch2 at rest before the treatment.
Figure 12. Ch2 at rest after the treatment.
The improvement obtained after the NPT treatment is evident at the simple inspection of the figures since they indicate a more periodic and arranged activity on muscle activity. In addition, in Appendix we report also the numerical results.
d) Chaos Analysis
As previously outlined, the basic finalities of this paper are to explore the NPT treatment of muscular dystro- phy by the use of non linear analysis. as a tool that is generally employed in the clinical and biomechanical applications. Accordingly, biomedical signals can be to an extent deterministic, random or chaotic. Deterministic signals have the characteristic of predictability. This is to say that any future time behaviour of the signal could be predicted using some linear analysis tools. For them, mathematical tools (e.g., Fourier transform) are commonly used. To use Fourier transform the signal must be linear, stationary and periodic. These are crucial restrictions that rarely we may find in biomedical signals governed from feedback control loops. The random signals are non-deterministic in the sense that individual data points of the signal may occur in any order, with no possibility of predictability on the future course of the signal. In this case only purely stochastic analytic tools can be applied in electrophysiology. Finally we have chaotic signals. These signals can be viewed as a connecting mesh between deterministic and unpredictable behavioural dynamics, exhibiting time pattern that in principle is slightly predictable, non-periodic or seldom quasi-periodic (an example is the heart beat) but they results strongly dependent from some control parameters and are highly sensitive to initial conditions. Dependence from control parameters means that for some critical values of such control parameters the chaotic system transitates between so much undefined states in time giving origin to a time dynamics that becomes unpredictable for us and thus apparently random but really revealing the signal an inner structure responding to the important realization of the self-organization and high complexity. The system whose counterpart has a chaotic signal as representation, reveals ability to self arrange by itself patterns of organization in its dynamics. This is of course the basic feature of living systems. Chaotic systems are non linear open systems, responding to the external stimuli by self-organizing each time their inner patterns and thus their time dynamics. All the considered systems in biomedicine are open systems that necessarily interact with their outside interacting systems and having time by time the fundamental demand to responds with elasticity to the requirements arriving from the external components. In this sense they self-organize their dynamics responding to inner and out inputs An example is the cardiovascular system that continuously needs self-organization responding to basic requirements of inner and output inputs and providing to heart rhythm variability, blood pressure, respiration, autonomic nervous system modulation, just to quote only some of the interacting components The other basic feature of chaotic systems is that they are highly sensitive to initial conditions. This is to say that each signal starts with some definite values of its variables. Consequently, a time dynamics is generated. In chaotic systems it is sufficient that such initial values of the variables fluctuate also at a so contained level to escape to our computational attention that consequently a total different time dynamics is generated with new and different properties in self-organization and structure to responds with elasticity to the requirements arriving from the external demands. Within chaos theory, the time series that are representative of the time dynamic of the chaotic signals are represented in the phase-space.
Embedded dimension in phase space is estimated by proper techniques that are autocorrelation method and, in particular, the average mutual information, estimating the so called time delay. Using the criterion of the False Nearest Neighbors we are enabled to obtain a proper representation in phase space reconstruction. Usually the analysis arrives to reconstruct the attractor of the given chaotic system and thus representing the states, the patterns and thus the subsequent transitions of the states characterizing the time dynamics of the system. Some indexes may be introduced to analyze chaotic systems. In particular we evaluate the Correlation Dimenion, the Largest Lyapunov Exponent, the Fractal dimension and LZ complexity.
Within biomedical signal processing, chaotic dynamics provide a possible explanation for the different complex and erratic patterns that appear in most bio-signals and in particular in electrophysiology. Current investigations span from studies of brain rhythms to heart rate variability, from blood pressure regulation to neuromuscular system, from breathing system to cardio-respiratory coordination including all the fields relating the complexity of the human and animal anatomo-physiological systems.
The reason to introduce non linear methodologies and chaos analysis in EMG has been explained previously. It is necessary to go on in further details.
The EMG and the sEMG signals are highly non-stationary signals. We know that the neuromuscular control process works through enhancing or inhibiting feedback mechanisms implemented on neuronal circuitry involving the Central Nervous System at various cortical or sub-cortical levels. In addition, we have constantly interaction o0f acting components and the result is a non linear and highly non stationary dynamics. In these conditions the adoption of non-linear chaotic methods is strongly required with the finality to account for the highly non-linear behaviour of such mechanisms by muscle receptors, mechanoreceptors, nociceptors, and joint receptors within local (spinal) and/or central sensory-motor networks. Only the use of non linear-chaotic mechanisms may contribute to elucidate such complex dynamics since non-linear parameters reveal several hidden mechanisms of muscle control that otherwise would be not reflected by variability of other standard linear parameters. In particular, as previously outlined, the RQA method looks at the inner structure of the given EMG signal. The proper reconstruction of the given sEMG signal in phase space is basic importance in RQA since by this way we identify recurrence maps containing subtle patterns that are often difficult to detect by visual inspection. In particular, by using such method, we have appropriate quantifying indexes, some quantitative descriptors that emphasize different features of the map. We previously described that we have four basic variables resulting from RQA analysis that are %REC, %REC, %Laminarity, Trapping Time, and Entropy Among them, percentage of determinism (%DET) must be used examined.
The reason of the basic importance of this index is that the %DET is strictly connected to the level of MU synchronization. sEMG signals generated by a model at sufficient level of MU synchronization shows an evident increase of the %DET parameter while passing from lower (a) to higher (b) levels of MU synchronization. Analogously, we may expect that a similar approach holds for the neuromuscular control system when the muscle task requires the maintenance of the effort for a long period of time. A greater synchronization of the MU activation will help to satisfy this request, despite the contemporaneously increased fatigue. Still, it is evident that, whereas very little differences in the relative spectra are reflected also in the MDF parameter weakly sensitive to the variation of the muscle status, increasing fatigue phenomena ask for a higher level of MU synchronization sensed by a parallel increase in the non-linear parameter %DET.
In the same manner, physiological studies indicate that during an increasing ramp, the relative timing of the phenomena is that at the beginning of the force ramp, there is an increasing level of MU recruitment followed by firing rate increase of the active MU. On the other hand, MU derecruitment takes place as soon as the rapid and little MU firstly recruited become fatigued. Finally the equilibrium between recruitment of the slower and bigger MUs and MU derecruitment determines the phase of MMUR (Maximal Motor Units Recruitment) corresponding to the highest level of MU activity in that muscle. In conclusion as a rule of the chaos non linear analysis in EMG signals, we recognize that that chaoticity increases at the beginning of the muscle task, as the result of further MUs recruitment, and then decreases in presence of fatigue phenomena and MUs synchronization.
In conclusion, the reason to use non linear chaotic methodologies and, in particular, the RQA, is that the use of nonlinear analysis and chaos theory provides an accurate investigation instrument, particularly by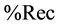 ,
,
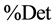 ,
,
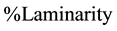 (
(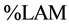 ), Trapping Time, and Entropy. In particular, %DET and possibly %REC and %LAM are able to detect the presence of repetitive hidden patterns in sEMG which, in turn, senses the level of MU synchronization within the muscle.
), Trapping Time, and Entropy. In particular, %DET and possibly %REC and %LAM are able to detect the presence of repetitive hidden patterns in sEMG which, in turn, senses the level of MU synchronization within the muscle.
Consequently, let us sketch our results such as correlation dimension D2, Largest Lyapunov exponent, L-Z complexity, fractal dimension. Numbers as 13.10.2014 and 17.10.2014 represent our inner classification relating respectively examination at rest before and after the treatment.
3.2. Correlation Dimension
On the basis of our previous studies on controls it results that at rest in sEMG we have usually a value of 2.7 ± 0.4 as D2 value of correlation dimension and a value of 3.80 ± 0.2 in condition of movement. In the present investigation we observed continuous transitions, exploring the condition of the subject minute by minute and we obtained the results that are given in Figure 13 and Figure 14 respectively for Ch1 and Ch2. Inspection of Figure 13 evidences that we had a net recovery in the D2 value after the treatment with a rather stable value, during the time transitions, remaining about 2.58 that enters in the normal range previously indicated. At rest before the treatment we had rather frequent transitions oscillating from a minimum of 1.668 to a maximum value of 3.618 both out of the normal range. In Ch2 at rest before the treatment we had continuous transitions with values ranging from a minimum value 0.178 to a maximum value of 2.917 still entering in the range of the normal values. After the treatment, the values of D2 stabilized about a value of 3.22 that is rather acceptable in consideration that in Ch2 we had the left trapeze (Ch2) that was almost atrophied as we confirm the clinical evaluation finding a value of 0.178 but still able to produce transitions arriving to 2.917 during transitions. The treatment stabilized such behaviour about the value of 3.22 that is not so distant from the normal value. Finally we have to remember here that in any case in EMG signals we have always noise corrupted time series and that all our results were always controlled by using surrogate data in order to dismiss the null hypothesis. The conclusion is
Figure 13. Estimation of correlation dimension in Ch1 at rest before and after therapy.
Figure 14. Estimation of correlation dimension in Ch2 at rest before and after therapy.
that the analyzed data confirmed that in sEMG we are in presence of a deterministic chaotic regime that we may delineate and quantify in detail. In particular, the results indicate that the used treatment induced unquestionable improvement.
3.3. Estimation of the Largest Lyapunov Exponent
As previously explained, the estimation of the Largest Lyapunov Exponent represents one important step in chaos analysis.
The Lyapunov exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories in the attractor Quantitatively, two trajectories of the attractor reconstructed in the phase space with initial separation δz0 diverge at a rate given by δz − δz0exp(λt) where λ is the Lyapunov exponent that we have to estimate. It is common to refer to the largest one as the Maximal Lyapunov exponent λE because it determines a notion of predictability for a dynamical system. A positive λE is usually taken as an indication that the system is chaotic. Obviously each result must be accepted only after control using surrogate data and evaluating the results with appropriate competence taking into account that we may have also other cases, out of chaotic systems, in which such exponent may result positive.
Let us look at the results of our analysis. The normal value for sEMG measurement on trapeze we have tabulated is λE = 0.068 ± 0.007 for health young subjects. By using surrogate data analysis we find that λE = 0.372 ± 0.008 as expected to confirm that we are actually examining a chaotic time dynamics. By these values the null hypothesis may be dismissed and we are sure that we are examining a chaotic muscular dynamics. The previous result relates obviously young subjects at rest for 3 minutes.
In the present case we examined right (Ch1) and left (Ch2) trapezes for a time of three minutes and we obtained the following results.
At rest first control in Ch1, λE = 0.147 ± 0.004 with surrogate data result λE =0.183 ± 0.006. Therefore we have the normal value λE = 0.068 ± 0.007 against λE = 0.147 ± 0.004 in the case of the examined muscular dystrophy. After the treatment we had the following estimated λE = 0.102 ± 0.006 (surrogate data value λE =0.163 ± 0.008). We verify that the treatment induced a strong improvement since λE = 0.068 ± 0.007 is our normal value. λE = 0.147 ± 0.004 before the treatment and λE = 0.102 ± 0.006 resulted after the treatment.
This is for the right trapeze. Let us examine now the results that we obtained for the left trapeze (Ch2).
At rest before the treatment we had λE = 0.101 ± 0.006 (the surrogate data analysis gave λE = 0.207 ± 0.008, thus confirming that also in this region muscular activity followed a chaotic regime). Left Trapeze resulted less chaotic respect to the λE value in the right trapeze with a strong unbalancing (λE = 0.147 ± 0.004 against λE = 0.101 ± 0.006) between the two (right-left) muscular dynamics. After the treatment, however, it resulted that λE = 0.115 ± 0.006 (surrogate data result λE = 0.190 ± 0.007). In conclusion, after the treatment we had λE = 0.102 ± 0.006 (Ch1) against λE = 0.115 ± 0.006 (Ch2) with a strong recovering in unbalancing situation. This was obtained by the treatment lowering strongly the chaoticity in Ch1 and increasing instead lightly the value in Ch2. This is confirmed of course from the results when we examined the attractor dimension by estimating the values of the Correlation Dimension in Ch1 and in Ch2. Looking at the Figure 13 and Figure 14 in fact one verifies that in Ch1 the value of the correlation dimension and thus the level of chaotic complexity decreases after the treatment while instead increased that one in Ch2.
3.4. LZ Complexity
It is well known that chaotic systems posses the basic relevant property of the self-organization. Such systems realize patterns that are self-arranged moving their time dynamics through stages on increasing complexity. Therefore it becomes of relevant interest to evaluate the level of complexity of the system during its dynamics. A measure of complexity in chaos analysis is reached by using the algorithmic of Lempel-Ziv that we used in this paper. The index varies between 0 and 1. Maximal complexity (represented by pure randomness) has a value of 1 and perfect predictability has a value of 0. Normal value in trapezes in young subjects has been estimated by us to be LZ = 0.23. In Ch1 we had LZ = 0.93 (high complexity) at rest before the treatment and this values decreased to LZ = 0.75 after the treatment. In Ch2, as well as in the case of the Correlation Dimension and Largest Lyapunov Exponet, we estimated the opposite. We had the initial value of LZ = 0.643 at rest before of the treatment and such value increased to LZ = 0.89 after the treatment again inducing balance between the two regions.
3.5. Recurrence Quantification Analysis
We may now go to examine the results that we obtained by using the previously mentioned Recurrence Quantification Analysis (RQA). In Figures 15-17 we give the results of the analysis performed on the Ch1 subject before of the treatment while in Figures 18-21 we have the corresponding results in Ch1 after the treatment. In Figures 22-24 we have the results in Ch2 before the treatment. In Figures 25-28 we have the corresponding results after the treatment. All the results are given by epochs of 1 second so that we may appreciate step by step the dynamics and the transitions that were involved.
In Picture 1 we have in detail the obtained results.
We repeat here that the indexes of the RQA to be estimated in each sEMG data analysis are the %Rec, the %Det, the %Lam, the Entropy and the Trapping Time. The reason is that they are able to detect and to quantify in detail the presence of repetitive hidden patterns in sEMG which, in turn, senses the level of MU synchronization within the muscle in reason of the particular pathology under investigation. In the reported table we give the results that we obtained by investigation of sEMG in epochs of 1 second., In this manner we performed a very accurate analysis (1 second) of the muscle dynamics and its transitions of the subject affected from muscular dystrophy. We performed the comparison of the obtained results for the subject at rest and before and after the treatment. The reader may inspect the obtained values for each epoch and every time compared before respect to after the treatment. It is possible to verify that we obtained an improvement of our RQA indexes in each epoch for Ch1 (right trapeze). All the variables %Rec, %Det, %Lam, Entropy and Trapping Time increased in a
Figure 15. RQA results on Ch1. Subject at rest before treatment. Each epoch is 1 second.
Figure 16. RQA results on Ch1. Subject at rest before treatment. Each epoch is 1 second.
very impressive manner after the treatment respect to before the treatment. Remember that, according to the results of the RQA analysis, an increasing value in %Rec, and %Det identify the percentage of repetitive hiddenpatterns in sEMG which, in turn, senses the level of MU synchronization within the muscle. %Det in particular characterizes chaos-order transitions, the duration of a stable interaction. Laminarity quantifies instead the level of chaos-chaos transitions in muscle with the Trapping Time index relates the time the muscle remains in a specific state. We found such parameters all increased. Finally also Entropy resulted increased after the treatment respect to before the treatment evidencing that the system reached a general level of relevant complexity. We obtained instead oscillating results in Ch2 (left trapeze) before respect to after the treatment. We had epochs in which the values of the previously mentioned variables of RQA prevailed before the treatment respect to after the treatment and epoch in which we had the vice versa. In substance, as said, Ch1 was placed on the right trapezes and Ch2 on the left Trapeze. We have to consider first of all that the trapezes, are very sensitive and reactive to the sympathetic nervous system so that the psychophysiological condition of the subject must be taken in consideration as we exposed in detail in a previous papers [9] [12] [14] . Obviously, an increase in sympathetic activity will contribute to tense up in the trapezes. In addition, in the dystrophic subject under consideration, clinical inspection evidenced that there was a very significant degree of muscle tension in his right trapezes (Ch1) compared to the much lesser degree of tension in his left trapezes (Ch2). So right from the very beginning, it was always going to be the case that there would be more improvement shown in Ch1 than any other channel In addition there is also a general neurological consideration that explains the importance, previously outlined, of our new methodology that mixes RQA analysis and time dynamics synchronization analysis devoted to the Ch1-Ch2
Figure 17. RQA results on Ch1. Subject at rest before treatment. Each epoch is 1 second.
Figure 18. RQA results on Ch1. Subject at rest after the treatment. Each epoch is 1 second.
Figure 19. RQA results on Ch1. Subject at rest after the treatment. Each epoch is 1 second.
and Ch8 (brain-EEG)-Ch1 and Ch8-Ch2 and that we will publish in detail in a subsequent paper. The reason involves the contra-lateral hemispheres of the brain. Ch1 is under the control of the left hemisphere of the brain and Ch2 under the control of the right hemisphere. What these data verify is that this subject had long term right hemisphere dominance. The subject was in a very right brain dominating state for a very long time and he had been a very angry impatient person. The distribution of energy in the brain was not bilaterally equal, therefore
Figure 20. RQA results on Ch1. Subject at rest after the treatment. Each epoch is 1 second.
Figure 21. RQA results on Ch1. Subject at rest after the treatment. Each epoch is 1 second.
Figure 22. RQA results on Ch2. Subject at rest before treatment. Each epoch is 1 second.
the left hemisphere adopted a permanent hyper protective state, which was then exhibited in the excessive muscle tension in his right trapezes. What the treatment enabled then, was for the distribution of energy and information in the system to become bilaterally stable, correcting these bilateral errors seen on the contralateral sides
Figure 23. RQA results on Ch2. Subject at rest before treatment. Each epoch is 1 second.
Figure 24. RQA results on Ch2. Subject at rest before treatment. Each epoch is 1 second.
Figure 25. RQA results on Ch2. Subject at rest after the treatment. Each epoch is 1 second.
of the body beneath the neck. All such data will be confirmed by inspection of the results on synchronization Ch1-Brain, Ch2-Brain that we will publish, as said, in the following paper.
Finally, returning to the RQA analysis, we have to outline that all the results were subsequently examined by ANOVA (as reported in the next Table 1) and the statistical investigation confirmed that we had the most
Figure 26. RQA results on Ch2. Subject at rest after the treatment. Each epoch is 1 second.
Figure 27. RQA results on Ch2. Subject at rest after the treatment. Each epoch is 1 second.
Figure 28. RQA results on Ch2. Subject at rest after the treatment. Each epoch is 1 second.
significant level of statistical significance in the compared data before and after the treatment.
4. Conclusions
First of all let us consider that the object of the present paper was to analyze muscular dystrophy by using standard
Picture 1. Results of recurrence quantification analysis performed on a time period of 3.33 minutes with epoch investigation of 1 minute.
Table 1. Statistical investigation of difference in results before and after therapy. All the results evidence high significance.
methodologies and nonlinear chaotic methods here including the RQA.
We have obtained results under different profiles.
First of all we have used all the procedures to test if sEMG signal is chaotic. Our result is that we have reached sufficient evidence that the sEMG signal contains a large chaotic component.
The following basic statements seem to be confirmed:
a) Chaoticity increases at the beginning of the muscle task, as the result of further MUs recruitment, and then decreases in presence of fatigue phenomena and MUs synchronization.
b) The use of the RQA method is essential in the sense that the %DET and possibly %REC and %LAM are able to detect the presence of repetitive hidden patterns in sEMG which, in turn, senses the level of MU synchronization within the muscle.
c) We have given detailed criteria to use nonlinear methodologies in sEMG analysis. The signal should be recorded at a frequency not lower than 960 Hz. Since the sEMG signal is affected from continuous transitions induced from its inner neuromuscular mechanisms and connecting directly chaotic dynamics, a correct investigation at physiology as well as clinic requires examining the recorded signal by epochs of 1 second in RQA and of 1 minute in estimation of the standard chaos indexes as estimation of the dimension of the attractor, D2, resulting fractal, largest Lyapunov exponent, and L-Z complexity.
Finally, we have obtained very encouraging results under the clinical profile. The NPT treatment, holding about chaotic mechanisms, gives a net improvement in muscular dystrophy.
To summarize we have to pose the following two basic questions.
What were the merits and demerits of this research using Chaos, Fractal and Recurrence Quantification Analysis method for surface electromyography?
What significance did this study have in the treatment of muscular dystrophy?
Let us attempt to give a detailed answer. Surface electromyography has been considered for years an electrophysiological signal having noise as basic components. Also according to some previous results that have been recently obtained in literature and that we have properly quoted, this interpretation is not correct. This signal, due to extremely complex network of interacting components, is intrinsically nonlinear and generating a complex dynamics that is fundamentally chaotic, fractal and also noise corrupted. As a consequence, the analysis of the sEMG requires the detailed application of the basic methods of the nonlinear analysis and in particular of chaos and fractal analysis and of the Recurrence Quantification Analysis (RQA) that is a fundamental methodology since it enables us to look at the inner structure of the investigated signal and quantify with detailed variables. The first merit is thus to have studied in detail a case of muscular dystrophy and to have confirmed with unquestionable results that this is really the dynamics of this signal. The second merit is that, using chaos, fractal and RQA analysis, we have given new indexes that are of immediate clinical application. In each case we have given the standard values in the case of normal subjects and we have compared these results with the case of the investigated pathology. It is evident that we have now new indexes of evaluation which are so sensitive to be able to characterize in detail the severity of the pathological condition of the case of muscular dystrophy that we have in examination. The third merit is that we have also given the modality of investigation. We have created a standard protocol of examination of the data that clinicians have, starting with the present paper, to follow in detail. We have attempted to standardize the frequency of sEMG recording and the epochs or windows to fragment the recorded signal in order to apply the nonlinear, chaotic, fractal methods and RQA. We have reached this result after a long work of standardization of the procedure attempting different ways of fragmentation of the recorded signal. We retain that mixing the previous results obtained from other authors and previously quoted with our direct and meticulous analysis, we have today a standardized procedure that may properly represent an actual advance under the clinical profile. Now let us examine the demerits. To perform a chaos analysis and RQA of given electrophysiological signal, no more is a simple matter. As outlined in the course of the present paper, it requires appropriate competence and use of appropriate methods such as the fundamental requirement to use surrogate data. Performing a chaos and fractal and RQA analysis requires adequate competence. Of course, as verified in detail here with a direct case and thus at the experimental level, the use of nonlinear methodologies is absolutely necessary. Therefore, there is software of analysis of sEMG in progress that as soon as possible we will realize and we will publish a subsequent article to illustrate it and give the opportunity to clinicians to use it. To finish there is the most important observation to be still added. The verification that sEMG contains a basic chaotic component is of enormous importance and we think that all the authors that have contributed, in addition to us, to such validation, deserve great consideration. The reason is that verifying the presence of chaos we understand that muscle dynamics is subject to continuous chaos-chaos transitions that obviously result to be so different in normal case respect to one of muscular dystrophy. The reason of the treatments in muscular dystrophy must reside in the possibility to rearrange the altered system about the normal possibilities of chaos-chaos transitions, self-organization and self-arrangement which is the peculiar feature of systems of high complexity subjected to a chaotic dynamics. The NTP treatment illustrated in [9] [12] [13] is resulting highly promising.
Cite this paper
ElioConte,KenWare,RiccardoMarvulli,GiancarloIanieri,MarisaMegna,SergioConte,LeonardoMendolicchio,EnricoPierangeli,11,11, (2015) Chaos, Fractal and Recurrence Quantification Analysis of Surface Electromyography in Muscular Dystrophy. World Journal of Neuroscience,05,205-257. doi: 10.4236/wjns.2015.54022
References
- 1. BioPac Systems. http://www.biopac.com/acqknowledge-data-acquisition-analysis-software-win
- 2. Conte, E., Todarello, O., Conte, S., Mendolicchio, L. and Federici, A. (2010) Methods and Applications of Non-Linear Analysis in Neurology and Psycho-Physiology. Journal of Consciousness Exploration & Research, 1, 1070-1138.
- 3. Conte, E., Pieralice, M., Laterza, V., Losurdo, A., Santacroce, N., Conte, S., Federici, A. and Giuliani, A. (2012) Traditional and a New Methodology for Analysis of Heart Rate Variability: A Review by Physiological and Clinical Experimental Results. International Journal of Research and Review in Applied Sciences, 3, 206-293.
- 4. Lei, M. and Meng, G. (2012) Nonlinear Analysis of Surface EMG Signals. In: Naik, G.R., Ed., Computational Intelligence in Electromyography Analysis—A Perspective on Current Applications and Future Challenges, Chapter 6. http://dx.doi.org/10.5772/49986
- 5. Sultorsarnace, S., Zeid, I. and Kamarthi, S. (2011) Classification of Electromyogtam Using RQA. Procedia Computer Science, 6, 375-380. http://dx.doi.org/10.1016/j.procs.2011.08.069
- 6. Farina, D., Merletti, R. and Enoka, R.M. (2004) The Extraction of Neural Strategies from Surface EMG. Journal of Applied Physiology, 96, 1486-1495. http://dx.doi.org/10.1152/japplphysiol.01070.2003
- 7. Farina, D., Fattorini, L., Felici, F. and Filligoi, G. (2002) Nonlinear Surface EMG Analysis to Detect Changes of Motor Unit Conduction Velocity and Synchronization. Journal of Applied Physiology, 93, 1753-1763. http://dx.doi.org/10.1152/japplphysiol.00314.2002
- 8. Morana, C., Ramdani, S., Perrey, S. and Varray, A. (2009) RQA of Surface Electromyographic Signal. Journal of Neuroscience Methods, 177, 73-79. http://dx.doi.org/10.1016/j.jneumeth.2008.09.023
- 9. Ware, K., Conte, E., Marvulli, R., Ianieri, G., Megna, M., Pierangeli, E., Conte, S., Mendolicchio, L. and Pellegrini, F. (2015) Case Report: Generalized Mutual Information (GMI) Analysis of Sensory Motor Rhythm in a Subject Affected by Facioscapulohumeral Muscular Dystrophy after Ken Ware Treatment. World Journal of Neuroscience, 5, 67-81. http://dx.doi.org/10.4236/wjns.2015.52008
- 10. Webber Jr, C.L. and Zbilut, J.P. (1984) Dynamical Assessment of Physiological Systems and States Using Recurrence Plot Strategies. Journal of Applied Physiology, 76, 965-973.
- 11. Ikegawa, S., Shinohara, M., Fukunaga, T., Zbilut, J.P. and Webber Jr, C.L. (2000) Nonlinear Time-Course of Lumbar Muscle Fatigue Using Recurrence Quantifications. Biological Cybernetics, 82, 373-382.
http://dx.doi.org/10.1007/s004220050591 - 12. Ware, K., Conte, E., Marvulli, R., Ianieri, G., Megna, M., Pierangeli, E., Conte, S. and Mendolicchio, L. (2015) Analysis of the Autonomic Regulation in a Case of Facioscapulohumeral Muscular Dystrophy after Ken Ware Treatment. World Journal of Neuroscience, 5, 162-173.
http://dx.doi.org/10.4236/wjns.2015.52018 - 13. Conte, E., Ware, K., Marvulli, R., Ianieri, G., Megna, M., Conte, S., Mendolicchio, L. and Pierangeli, E. (2015) Heart Rate Variability: On the Importance to Perform HRV Analysis in Subjects Affected from Muscular Dystrophy. World Journal of Cardiovascular Diseases, 5, 141-149.
http://dx.doi.org/10.4236/wjcd.2015.56017 - 14. Clancy, E.A. and Hogan, N. (1997) Theoretic and Experiment Comparison of Root-Mean-Square and Mean-Absolute-Value Electromyogram Amplitude Detectors. Proceedings of the 19th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 3, 1267-1270.
Appendix
Ch1 at rest before the treatment.
Ch1 after the treatment.
Ch2 before the treatment.
Ch2 after the treatment.
NOTES
*Corresponding author.








































































































