Open Journal of Ecology
Vol.05 No.01(2015), Article ID:53036,12 pages
10.4236/oje.2015.51001
Bayesian Estimation of Population Size via Capture-Recapture Model with Time Variation and Behavioral Response
Xiaoyin Wang1, Zhuoqiong He2, Dongchu Sun2
1Department of Mathematics, Towson Univeristy, Towson, MD, USA
2Department of Statistics, University of Missouri-Columbia, Columbia, MO, USA
Email: xwang@towson.edu, hezh@missouri.edu, sund@missouri.edu
Academic Editor: Victor R. Savage, National University of Singapore, Singapore
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 November 2014; revised 29 November 2014; accepted 15 December 2014
ABSTRACT
We consider the problem of population estimation using capture-recapture data, where capture probabilities can vary between sampling occasions and behavioural responses. The original model is not identifiable without further restrictions. The novelty of this article is to expand the current research practice by developing a hierarchical Bayesian approach with the assumption that the odds of recapture bears a constant relationship to the odds of initial capture. A real-data example of deer mice population is given to illustrate the proposed method. Three simulation studies are developed to inspect the performance of the proposed Bayesian estimates. Compared with the maximum likelihood estimates discussed in Chao et al. (2000), the hierarchical Bayesian estimate provides reasonably better population estimation with less mean square error; moreover, it is sturdy to underline relationship between the initial and re-capture probabilities. The sensitivity study shows that the proposed Bayesian approach is robust to the choice of hyper-parameters. The third simulation study reveals that both relative bias and relative RMSE approach zero as population size increases. A R-package is developed and used in both data example and simulation.
Keywords:
Bayes Estimation, Behavioural Response, Capture-Recapture Model, Gibbs Sampling, Hierarchical Prior, Population Estimation, Time Variation

1. Introduction
The capture-recapture sampling methods were originally designed to estimate wildlife populations. They are now widely applied to numerous areas, such as biology and ecology for estimating animal and plant populations, sociology and demography for estimating the size of the population at risks, official statistics for census undercount procedures, economics and finance in credit scoring and fraud detection, and so on. Varieties of methods have been developed to analyse these models, such as maximum likelihood [1] -[6] , moment methods based on sample coverage [7] - [9] , martingales [10] - [12] , and Bayesian methods [13] - [23] , and so forth. With the rapid growth in both methodology and application, the literature on capture-recapture analysis is tremendously massive. For a comprehensive literature review on capture-recapture models, see [24] - [29] .
In this paper, we focus on inferences for the closed population capture-recapture experiment with capture probabilities being assumed to vary with time (or sampling occasion) and behavioral response. This model was originally proposed by Pollock in his doctoral dissertation (1974), and was referred to as the model 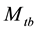 in the literature, where the subscript t denotes the time (or sampling occasions) and b denotes the behavioral response; see Otis et al. [5] . The behavioral response means that animals change their behavior after their initial captures. Animals might become “trap-happy” if being caught is rewarding (getting food from a baited trap, for example) or “trap-shy” if being caught is traumatic (having a plastic tag stapled through the ear, for example). The model
in the literature, where the subscript t denotes the time (or sampling occasions) and b denotes the behavioral response; see Otis et al. [5] . The behavioral response means that animals change their behavior after their initial captures. Animals might become “trap-happy” if being caught is rewarding (getting food from a baited trap, for example) or “trap-shy” if being caught is traumatic (having a plastic tag stapled through the ear, for example). The model 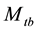 assumes that on a given sampling occasion all unmarked animals have one probability of capture and all marked animals have another probability of capture, and it assumes that these probabilities vary from one sampling occasion to another.
assumes that on a given sampling occasion all unmarked animals have one probability of capture and all marked animals have another probability of capture, and it assumes that these probabilities vary from one sampling occasion to another.
The model 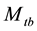 is important in practice because animals often exhibit a behavioural response to capture. This model has been selected as the most likely model in some population-estimation studies obw78, pnbh90. The original
is important in practice because animals often exhibit a behavioural response to capture. This model has been selected as the most likely model in some population-estimation studies obw78, pnbh90. The original 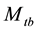 model is not identifiable without further restrictions on the parameters because the number of unknown parameters is more than that of the minimal sufficient statistics. In order to make the parameters estimable, one may assume that at least two of the capture probabilities are equal. However, there is no biological justification for making such an assumption [5] . Tanaka [30] [31] suggested a regression procedure, which had serious problems of interpretation [32] . Another assumption considered by Otis et al. [5] is that the ratio of the recapture probability to the initial capture probability is a constant. Chao et al. [2] derived the unconditional MLE (UMLE), the conditional MLE (CMLE) and the maximum quasi-likelihood (MQLE) estimators under this assumption without putting a minimal constraint on the constant ratio to ensure that neither initial nor recapture probabilities exceed 1.0. Under the same constant ratio assumption and with the minimal constraint of the constant ratio embedding in the MCMC, Lee and Chen [20] and Lee et al. [21] derived Bayes estimate by applying Beta prior to the initial capture probability and Uniform prior on the constant ratio. The results show that the performance of the estimate often depends on the choice of the hyper-parameters in the prior distributions. [19] proposed a Bayesian analysis of all eight closed population capture-recapture models within a logistic regression frame work. The method was illustrated through two real data samples, and the results are compared with those from MARK, which is a free software for capture-recapture data using classical MLE approach. Unfortunately, neither data set was determined to be suitable to the model
model is not identifiable without further restrictions on the parameters because the number of unknown parameters is more than that of the minimal sufficient statistics. In order to make the parameters estimable, one may assume that at least two of the capture probabilities are equal. However, there is no biological justification for making such an assumption [5] . Tanaka [30] [31] suggested a regression procedure, which had serious problems of interpretation [32] . Another assumption considered by Otis et al. [5] is that the ratio of the recapture probability to the initial capture probability is a constant. Chao et al. [2] derived the unconditional MLE (UMLE), the conditional MLE (CMLE) and the maximum quasi-likelihood (MQLE) estimators under this assumption without putting a minimal constraint on the constant ratio to ensure that neither initial nor recapture probabilities exceed 1.0. Under the same constant ratio assumption and with the minimal constraint of the constant ratio embedding in the MCMC, Lee and Chen [20] and Lee et al. [21] derived Bayes estimate by applying Beta prior to the initial capture probability and Uniform prior on the constant ratio. The results show that the performance of the estimate often depends on the choice of the hyper-parameters in the prior distributions. [19] proposed a Bayesian analysis of all eight closed population capture-recapture models within a logistic regression frame work. The method was illustrated through two real data samples, and the results are compared with those from MARK, which is a free software for capture-recapture data using classical MLE approach. Unfortunately, neither data set was determined to be suitable to the model , and the merit of the method with the model
, and the merit of the method with the model  remains undiscovered. Also, there is no discussion about the performance of the Bayes estimates with different possible of capture probabilities and/or different population sizes. Regarding the prior specification, [19] performs a limited prior sensitivity analysis in the second example and concludes that the different prior specification has relatively little influence on the final estimation. However, in the same example, it also points out that “the prior specified on the individual variance component appeared to be somewhat restrictive in this case, with values supported by the data having relatively small prior mass”. Therefore, the choice of the hyper-para- meter remains ambiguous. We are thus motivated to explore more reasonable restrictions to deal with the non-identification, and to find more robust population estimation of the model
remains undiscovered. Also, there is no discussion about the performance of the Bayes estimates with different possible of capture probabilities and/or different population sizes. Regarding the prior specification, [19] performs a limited prior sensitivity analysis in the second example and concludes that the different prior specification has relatively little influence on the final estimation. However, in the same example, it also points out that “the prior specified on the individual variance component appeared to be somewhat restrictive in this case, with values supported by the data having relatively small prior mass”. Therefore, the choice of the hyper-para- meter remains ambiguous. We are thus motivated to explore more reasonable restrictions to deal with the non-identification, and to find more robust population estimation of the model  in the Bayesian framework with more objective prior distribution, and the results are compared to the state-of-art MLE as proposed in [2] .
in the Bayesian framework with more objective prior distribution, and the results are compared to the state-of-art MLE as proposed in [2] .
R is a free software programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians and data miners for developing statistical software and data analysis. In this paper, a R-package named sbmtb is created and used within the data analysis and simulation studies.
In this paper, we assume that the odds ratio of recapture probability and initial probability is a constant, as was initially proposed by Wang [22] in her doctoral dissertation; hierarchical prior distributions with vague information are assigned to the unknown parameters after logistic transformation; and Markov chain Monte Carlo (MCMC) methods are used to implement the Bayesian computation. The MCMC methods allow us to construct an ergodic Markov chain with stationary posterior distribution and, furthermore, to obtain the posterior quantities of the parameters of interest. Full conditional distributions are used in the MCMC methods to obtain approximations of the posterior distributions and Bayes estimates of the posterior quantities of unknown parame- ters.
Otis et al. [5] provides an interesting data set on the deer mice study that was also used by Chao et al. [2] Altogether, there are 110 distinct mice caught out of 283 captures in 5 consecutive days. This same data set is used here to illustrate the proposed Bayesian approach of population estimation.
Simulation studies are conducted to confirm the findings in the example, and to examine the performance of the proposed Bayesian approach. Compared with the state-of-the-art maximum likelihood estimates derived by Chao et al. [2] , the proposed Bayesian estimates provide a relative comparable population estimation with smaller standard error and mean square error, especially when the overall capture probability is low. In addition, the Bayesian estimate relies little on the underlying relationship between initial and recapture probabilities. An intensive prior sensitivity study shows that the proposed Bayesian inference remains robust with different values of prior distributions. The third simulation study shows some of the asymptotic properties of the proposed Bayes estimate such that both relative bias and mean square error fade away as the population size increases.
In Section 2.1, we briefly review the problem of non-identifiability and propose a novel restriction, in which the odds ratio of recapture probability and initial probability is a constant. In Section 2.2, we apply the hierarchical prior to the unknown parameters in the model, and put forward a objective approach to determine the hyper-parameters in the prior distributions. In Section 2.3, we derive full conditional posterior distributions of the unknown parameters for the MCMC algorithm. In Section 3, we use a real data example to illustrate the proposed Bayesian hierarchical estimation approach. In Section 4, we conduct simulation studies to examine the performance of the proposed Bayesian approaches. In Section 5, we conclude and give remarks.
2. Bayesian Analysis of Model 
2.1. Likelihood Function
We assume that the population size is N, and there are k sampling occasions. On the  sampling occasion, let
sampling occasion, let  denote the initial capture probability, or the probability of an unmarked animal being captured on the
denote the initial capture probability, or the probability of an unmarked animal being captured on the 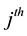 sampling occasion, and
sampling occasion, and 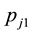 be the recapture probability, or the probability of a marked animal being captured. The likelihood proposed by [5] for the model
be the recapture probability, or the probability of a marked animal being captured. The likelihood proposed by [5] for the model 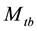 is
is
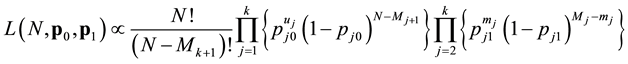 (1)
(1)
where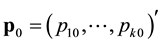 ,
, 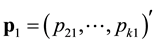 ,
, 










We propose a restriction based on the odds of initial capture and recapture, as is initially discussed in [22] (unpublished doctoral dissertation). Odds (in favor of an event) is defined as the ratio of the probability that the event will happen to the probability that the event will not happen. It is an expression of relative probabilities, which other research studies have found to be more convenient to use than probabilities. We assume that the odds of recapture bears a constant relationship to the odds of initial capture, i.e.,

This assumption says that on a given sampling occasion, the odds of recapture is proportional to that of the initial capture. In a “trap happy” situation, the proportion r is greater than 1.0, and in a “trap shy” situation, r is less than 1.0. When there is no behavioural response,
Comparing the proposed constraint with the constant ratio constraint, which presumes that

The Equation (2) then becomes

with










Let 


where 







2.2. Priors
We apply Bayesian approaches to the re-parametrized likelihood Function (4) to estimate the population size N with the hierarchical prior. For

In the second stage, another Normal distribution prior is applied to


and

where


The prior distribution of 

where 


and

where


The hyper-parameters are chosen using vague information as follows. If the initial capture probability is assumed to be between 
























For the prior distribution of N, the Poisson-Gamma type of hierarchical prior is a popular choice in the literature [33] -[37] . In the first stage, the unknown population size N is assumed to have a Poisson distribution with mean

In the second stage, 



The marginal prior distribution of

In the situation where little information about 










2.3. Bayesian Computation
The population size N is the parameter of interest. Under the square error loss function, the posterior mean is the Bayesian estimator. However, the closed form expression of the posterior distribution of N is not easy to achieve. Therefore, we will use Markov chain Monte Carlo (MCMC) methods to obtain numerical solutions. In order to implement the MCMC procedure, it is necessary to have the full conditional posterior distributions, which are the conditional distributions of one parameter given all the other unknown parameters and data.
The full conditional posterior distributions of 

・
・ For
・
・
・
・
・
・ 
The conditional distributions of 



the conditional density function 
3. Real Data Examples
Otis et al. [5] provides an interesting data set of deer mice. The data were collected by S. Hoffman (pers. comm.) in mid-July 1974. Trapping was on 5 consecutive mornings, and 110 distinct mice were caught. It is assumed that there exists time and behavioural response of capture. The summary statistics are presented in Table 1. This data set is also used in Chao et al. [2] , Lee and Chen [20] , Lee et al. [5] .
We use a Gibbs sampler in the R-package to implement the Bayesian computation. The burn-in stage is 15,000 iterations. The samples from the next 10,000 iterations are taken to construct the approximate posterior distribution of N. The Bayesian estimate of the population size N is



The Bayesian estimate is very similar to the UMLE with a smaller standard error. It is also smaller than the CMLE, with a smaller standard error and is greater than the QMLE with a slightly greater standard error. The Bayesian estimates of initial capture probabilities are also computed as





It is worth noting that the estimated behavioural effect 
Table 1. Summary data of deer mice example.
4. Simulation Studies
Chao et al. [2] reports a simulation study with the true population size of 400 and 8 different initial capture probabilities, with the recapture probabilities being calculated as
Several frequentist quantities are considered, such as bias, relative bias (which is the ratio of bias to the true population size), root mean square error (RMSE), and relative RMSE (which is the ratio of RMSE to the true population size) of Bayesian estimates of the population size. Suppose 



In the simulation, we generate capture histories 1000 times under each set of true parameters. The results of bias, relative biases (in parenthesis), RMSE, and relative RMSE (in parenthesis) are listed in Table 3. When the mean catchability is relatively low (cases 1 - 4), in terms of bias and relative bias, Bayesian estimates are very close to the two preferred MLE’s (CMLE and MQLE) in Chao et al. [2] ; while, Bayesian estimates consistently have smaller RMSE’s than the three MLE’s. In case 3, the bias of the Bayesian estimate is slightly greater than the MQLE with about 4% difference; however, there is about 10% of drop in RMSE when using the Bayesian estimate. As previously mentioned, when it comes down to practice, it is not uncommon to trade off some increase in bias for a larger decrease in the variance. Therefore, we would prefer the Bayesian estimate to the MLE’s in these cases. When there is a sufficient number of captures (cases 5 - 8), according to Chao et al. [2] , the UMLE is preferable to the other two estimators. Compared with the UMLE in these cases, the Bayesian approach yields comparable estimates in cases 5 and 8 with less RMSE. In case 7, the Bayesian estimate has a slightly larger bias than the UMLE, with a difference of less than 3%, but the RMSE dropped more than 3%. In case 6, the Bayesian estimate has a slightly larger bias with similar RMSE than the UMLE. Given the fact that the Bayesian estimates always provide a smaller RMSE than the three MLE’s with comparable or slightly larger bias, we would conclude that the proposed Bayesian approach provides reasonably better estimation than the three MLE’s.
It is worth mentioning that the simulated data was based on the constant ratio of initial and re-capture probabilities as in Chao et al. [2] rather than the constant odds ratio as we proposed. The conclusion that Bayesian estimates still outperform the MLE’s, to a certain extent, indicates that the former one is robust to the constraints between the initial and recapture probabilities.
An usual difficulty of the Bayesian analysis is the need to specify prior distributions when little information is available for guidance. Here, we will examine how the proposed Bayesian inference is influenced by the choice
Table 2. Capture probabilities and behavioural effect parameter in simulation study I.
Table 3. Comparison of bayesian estimations with MLE’s.
of different values of the hyper-parameters of the prior distribution. As described in Section 2.2, the presumed range of the capture probability is utilized to determine the value of hyper-parameters 



The third simulation study examines the performance of the Bayesian estimation with different population sizes from 100 to 1000. We use the initial capture probabilities in cases 1, 2, and 8 in Table 2, representing low, medium low, and high capture probabilities, respectively. The behavioural effect parameter 
Table 4. Sensitivity of the bayes estimation to the specification of the prior probability distributions.
5. Conclusions and Remarks
In this paper, we propose a Bayesian hierarchical approach to estimate the population size of model 


We were inspired to propose a new constraint so that the odds ratio of recapture probability and initial capture probability remains a constant and to analyse the model 


Figure 1. Relative bias and RMSE of bayesian population estimations.
Note that the findings here are mostly based on simulation results. It would be interesting to examine the theoretical bias and MSE of the Bayesian estimate under the hierarchical prior distribution studied in this paper. We’ll continue studying more complex models such as

Author’s Contribution
A R-package named sbmtb is created and used within the data analysis and simulation studies in the paper. The detailed help manual is in the Appendix. The R-package is available via e-mail request to Xiaoyin Wang at xwang@towson.edu.
References
- Agresti, A. (1994) Simple Capture-Recapture Models Permitting Unequal Catch Ability and Variable Sampling Effort. Biometrics, 50, 494-500. http://dx.doi.org/10.2307/2533391
- Chao, A., Chu, W. and Hsu, C. (2000) Capture Recapture When Time and Behavioral Response Affect Capture Probabilities. Biometrics, 56, 427-433. http://dx.doi.org/10.1111/j.0006-341X.2000.00427.x
- Norris III, J.L. and Pollock, K.H. (1995) A Capture-Recapture Model with Heterogeneity and Behavioural Response. Environmental and Ecological Statistics, 2, 305-313. http://dx.doi.org/10.1007/BF00569360
- Norris, J.L. and Pollock, K.H. (1996) Nonparametric MLE under Two Closed Capture-Recapture Models with Heterogeneity. Biometrics, 52, 639-649.
- Otis, D.L., Burghal, K.P., White, G. and Anderson, D. (1978) Statistical Inference from Capture Data on Closed Animal Populations. Wildlife Monographs, 62, 1-135.
- Pledger, S. (2000) Uniffed Maximum Likelihood Estimates for Closed Capture-Recapture Models Using Mixtures. Biometrics, 56, 434-442. http://dx.doi.org/10.1111/j.0006-341X.2000.00434.x
- Chao, A., Lee, S.M. and Jeng, S.L. (1992) Estimating Population Size for the Capture-Recapture Data When Capture Probabilities Very by Time and Individual Animal. Biometrics, 48, 201-216. http://dx.doi.org/10.2307/2532750
- Lee, S.M. (1996) Estimating Population Size for Capture-Recapture Data When Capture Probabilities Vary by Time, Behavior and Individual Animal. Communications in Statistics-Simulation, 25, 431-457.
- Lee, S.M. and Chao, A. (1994) Estimating Population Size via Sample Coverage for Closed Capture-Recapture Model. Biometrics, 50, 80-97. http://dx.doi.org/10.2307/2533199
- Yip, P. (1989) An Inference Procedure for a Capture and Recapture Experiment with Time-Dependent Capture Probabilities. Biometrics, 45, 471-479. http://dx.doi.org/10.2307/2531490
- Yip, P. (1991) A Martingale Estimating Equation for a Capture-Recapture Experiment in Discrete Time. Biometrics, 47, 1081-1088. http://dx.doi.org/10.2307/2532660
- Yip, P.S.F. and Fong, D.Y.T. (1993) Estimating Population Size by Recapture Sampling via Estimating Function. Communications in Statistics-Stochastic Models, 9, 179-193. http://dx.doi.org/10.1080/15326349308807261
- Basu, S. and Ebrahimi, N. (2001) Bayesian Capture-Recapture Methods for Error Detection and Estimation of Population Size Heterogeneity and Dependence. Biometrika, 88, 269-279. http://dx.doi.org/10.1093/biomet/88.1.269
- Bolfarine, H., Leite, J.G. and Rodrigues, J. (1992) On the Estimation of the Size of a Finite and Closed Population. Biometrical Journal, 34, 577-593. http://dx.doi.org/10.1002/bimj.4710340507
- Castledine, B.J. (1981) A Bayesian Analysis of Multiple-Recapture Sampling for a Closed Population. Biometrika, 68, 197-210. http://dx.doi.org/10.1093/biomet/68.1.197
- Chavez-Demoulin, V. (1999) Bayesian Inference for Small Sample Capture-Recapture Data. Biometrics, 55, 727-731. http://dx.doi.org/10.1111/j.0006-341X.1999.00727.x
- Dupuis, J.A. (1995) Bayesian Estimation of Movement and Survival Probabilities from Capture-Recapture Data. Biometrics, 82, 761-772.
- Gazey, W.J. and Staley, M.J. (1986) Population Estimation from Mark-Recapture Experiments Using a Sequential Bayes Algorithm. Ecology, 67, 941-951. http://dx.doi.org/10.2307/1939816
- King, R. and Brooks, S. (2008) On the Bayesian Estimation of a Closed Population Size in the Presence of Heterogeneity and Model Uncertainty. Biometrics, 64, 816-824. http://dx.doi.org/10.1111/j.1541-0420.2007.00938.x
- Lee, S.M. and Chen, C.W.S. (1998) Bayesian Inference of Population Size for Behavioral Response Models. Statistical Sinica, 8, 1233-1247.
- Lee, S.M., Hwang, W.H. and Huang, L.H. (2003) Bayes Estimation of Population Size from Capture-Recapture Models with Time Variation and Behavior Response. Statistical Sinica, 13, 477-494.
- Wang, X. (2002) Bayesian Analysis of Capture-Recapture Sampling for a Closed Population. Ph.D. Dissertation, University of Missouri-Columbia, Columbia.
- Wang, X., He, Z. and Sun, D. (2007) Bayesian Population Estimation for Small Sample Capture-Recapture Data Using Non-Informative Prior. Journal of Statistical Planning and Inference, 137, 1099-1118. http://dx.doi.org/10.1016/j.jspi.2006.03.004
- Amstrup, S.C., McDonald, T.L. and Manly, B.F.J. (2005) Handbook of Capture Recapture Analysis. Princeton University Press, Princeton.
- Chao, A. (2001) An Overview of Closed Capture-Recapture Models. Journal of Agricultural, Biological, and Environmental Statistics, 6, 158-175. http://dx.doi.org/10.1198/108571101750524670
- Pollock, K.H., Nichols, J.D., Brownie, C. and Hines, J.E. (1990) Statistical Inference for Capture-Recapture Experiments. Wildlife Monographs, 107, 1-97.
- Schwarz, C.J. and Seber, G.A.F. (1999) Estimating Animal Abundance: Review III. Statistical Science, 14, 427-456. http://dx.doi.org/10.1214/ss/1009212521
- Seber, G.A.F. (1992) A Review of Estimating Animal Abundance II. International Statistical Review, 60, 129-166. http://dx.doi.org/10.2307/1403646
- Williams, B.K., Nichols, J.D. and Conroy, M.J. (2002) Analysis and Management of Animal Populations. Academic Press, San Diego.
- Tanaka, R. (1951) Estimation of Vole and Mouse Population on Mount Ishizuchi and on the Uplands of Southern Shikoku. Journal of Mammalogy, 32, 450-458. http://dx.doi.org/10.2307/1375793
- Tanaka, R. (1952) Theoretical Justification of the Mark and Release Index for Small Mammals. Bulletin of the Kochi Women’s College, 1, 38-47.
- Seber, G. (1973) The Estimation of Animal Abundance and Related Parameters. Griffin, London.
- George, E.I. (1992) Capture-Recapture Estimation via Gibbs Sampling. Biometrika, 79, 677-683.
- Raftery, A.E. (1987) Inference and Prediction for General Order Statistic Model. Journal of the American Statistical Association, 82, 1163-1168. http://dx.doi.org/10.1080/01621459.1987.10478554
- Raftery, A.E. (1988) Analysis of Simple Debugging Model. Applied Statistics, 37, 12-32. http://dx.doi.org/10.2307/2347490
- Raftery, A.E. (1988) Inference for the Binomial N Parameter: A Hierarchical Bayes Approach. Biometrika, 75, 223- 228. http://dx.doi.org/10.1093/biomet/75.2.223
- Smith, P.J. (1991) Bayesian Analysis for a Multiple Capture-Recapture Model. Biometrika, 78, 399-407. http://dx.doi.org/10.1093/biomet/78.2.399
- Gilk, W. (1992) Derivative-Free Adaptive Rejection Sampling for Gibbs Sampling. In: Bernardo, J.M., Beger, J.O., Dawi, A.P. and Smith, A.F.M., Eds., Bayesian Statistics 4, Oxford University Press, Oxford, 641-649.
Appendix
Package ‘sbmtb’
September 18, 2014
Type Package
Title Bayesian Analysis of Capture-Recapture Model with Time Variation and Behavioral Response
Version 1.0
Date 2014-09-18
Author Xiaoyin Wang
Maintainer Xiaoyin Wang < xwang@towson.edu >
Description
Bayesian Analysis of Capture-Recapture Model with Time Variation and Behavioral Response
License GPL-2
Depends ars
R topics documented:
sbmtb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
sbmtb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Description
Bayesian analysis of Capture-Recapture model with time variation and behavioral response
Details
Package: sbmtb
Type: Package
Version: 1.0
Date: 2014-09-18
License: GPL-2
Depends: ars
1
2 sbmtb
Author(s)
Xiaoyin Wang <xwang@towson.edu>
References
X. Wang, Z. He and D. Sun Bayesian Estimation of Population Size via Capture-Recapture Model with Time Variation and Behavioral Response, Open Jounal of Ecology
Examples
n.days<-5
um.cap<-c(37,31,9,21,12)
mm.cap<-c(0,23,49,44,57)
sbmtb(n.days,um.cap, mm.cap)
Description
This function provides Baysian analysis of capture-recapture model with time variation and behavioral response. It calculates the posterior mean, standard deviation and confidence interval of the population size, capture probability and behavioral effect.
Usage
sbmtb(n.days, u.cap, m.cap)
Arguments
n.days Number of capture occasions
u.cap a vector of number of unmarked/new captures on each capture occasion
m.cap a vector of number of marked/recaptures on each capture occasion
Value
Population a data frame contains the posterior mean, standard deviation, and confidence interval of the population size
Probability a data frame contains the posterior mean, standard deviation, and confidence interval of the capture probabilities
behavior a data frame contains the posterior mean, standard deviation, and confidence interval of the behavior effect
Author(s)
Xiaoyin Wang
sbmtb 3
Examples
n.days<-5
um.cap<-c(37,31,9,21,12)
mm.cap<-c(0,23,49,44,57)
sbmtb(n.days,um.cap, mm.cap)














