Open Journal of Ecology
Vol.4 No.11(2014), Article
ID:48755,10
pages
DOI:10.4236/oje.2014.411055
Comparisons and Contrasts between Asymmetry and Nestedness in Interacting Ecological Networks
Gilberto Corso1*, N. F. Britton2
1Departamento de Biof sica e Farmacologia, Centro de Biociências, Universidade Federal do Rio Grande do Norte, Natal-RN, Brazil
2Department of Mathematical Sciences and Centre for Mathematical Biology, University of Bath, Bath, UK
Email: *corso@cb.ufrn.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 June 2014; revised 3 July 2014; accepted 15 July 2014
ABSTRACT
We compare and contrast asymmetry and nestedness, two concepts used in the characterisation of the specialist-generalist balance in bipartite ecological interaction networks. Our analysis is relevant to mutualistic networks such as those consisting of flowering plants and pollinators, or fruiting plants and frugivores, or antagonistic networks such as those consisting of plants and herbivores, in an ecological community. We shall refer to the two sets of species in the bipartite network as plants and animals, the usual but not the only ecological situation. By asymmetry we mean either connectivity asymmetry or dependence asymmetry, which are essentially equivalent. Asymmetry expresses two attributes: generalists interact preferentially with specialists, and specialists avoid interacting with each other. Nested patterns, in principle, should express these same two features and one more: the presence of a core of interactions among generalists. We compute the full set of perfectly nested patterns that are possible in an L × L matrix with N interactions, representing an ecological network of L plants and L animals, and point out that the number of nested arrangements grows exponentially with N. In addition, we analyse asymmetry for the full set of perfectly nested patterns, and identify extremes of asymmetry inside the universe of nested patterns. The minimal asymmetry is marked by a modular core of interactions between species that are neither specialists nor generalists. On the other hand, the case of maximal asymmetry is formed by a set of few generalists and many specialists with equal connectivity. The stereotypic case of nestedness with a core of interactions among generalists has intermediate asymmetry.
Keywords:Bipartite Interaction Networks, Nestedness, Asymmetry, Ecology of Communities

1. Introduction
The contemporary way to look at an ecological community is through the lens of an interaction network; in this approach the pattern formed by the interactions is more important than the particular species that take part in the tangled interplay of the interactions. Despite the widespread acceptance for employing networks as good theoretical models to investigate ecological communities, their characterisation remains a delicate matter. Many tools from network theory and statistics have been used in this enterprise [1] -[4] , but not all are based on a clear mathematical background, and this leads to possible ambiguity.
A scientific theory should employ intelligible concepts to produce clear statements, otherwise any attempt at falsification will be ineffective or dubious. We state this methodological remark because the aim of this paper is to clarify concepts. We shall focus on two concepts that are used, and sometimes interchanged, to understand the specialist-generalist balance in bipartite interaction networks (BINs): asymmetry and nestedness.
The ecological idea behind connectivity asymmetry is that generalist species are typically connected to specialists. Such a pattern may contribute to stability [5] -[7] . In an abstract way, we can formulate connectivity asymmetry as the following principle: species tend to interact with species with the maximum possible difference in their number of interactions. Specialists tend to interact with generalists, and neither generalists nor specialists tend to interact with each other. We shall see later that connectivity asymmetry is essentially equivalent to dependence asymmetry, where species prefer to interact with species with the maximum possible difference in their dependences on each other. Asymmetry indices may be defined for qualitative networks, where information is only available on whether or not plant species i interacts with animal species j, or for quantitative networks, where in addition the strength of the interaction is quantified. In the literature, dependence asymmetry was explored initially for qualitative networks by Vásquez and Aizen [8] , and then for quantitative networks by Bascompte and co-authors [9] and, using an entropy-based approach, by Blüthgen and co-authors [10] .
Nestedness was first introduced to describe patterns of species composition on islands [11] , then adapted to describe patterns that commonly occur in plant-pollinator BINs by [12] , and had been used widely to describe many BINs. A nested BIN contains, at the same time, three different aspects [13] : 1) a core of generalists that interact with other generalists; 2) many generalists that interact with specialists; and 3) an absence of interactions between specialists. Nestedness indices are normally only defined for qualitative networks. Although there is no consensus in the literature about the best way to define an index to quantify nestedness [11] , most authors agree that a gap-free matrix is perfectly nested [14] [15] . It means that, once we place rows and columns in decreasing order of their sums, the final matrix representation of a perfectly nested BIN should contain no empty site with an occupied site to its right or below it.
In this methodological manuscript we proceed by comparison, exploring similarities and contrasts between asymmetry and nestedness. Since nestedness indices for BINs are based on qualitative data, the comparison requires us to use qualitative data for measures of asymmetry as well. We start by introducing connectivity asymmetry for qualitative networks and stating its main properties, and show that it is equivalent to dependence asymmetry. After that we take a matrix of given size and occupancy, and give an asymptotic expression for the number of possible perfectly nested arrangements. We then calculate the connectivity asymmetry for all perfectly nested arrangements, focusing on the nested patterns of maximal and minimal asymmetry. In the conclusion, we discuss the results in the context of the literature of BINs, and explore the possibility of employing connectivity asymmetry as a tool in the analysis of qualitative BINs.
2. Theoretical Analysis
Before we begin the theoretical study, let us fix the mathematical notation we shall use throughout the article. The central mathematical concept is the adjacency matrix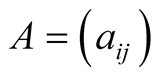 , where
, where 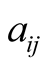 is defined by
is defined by
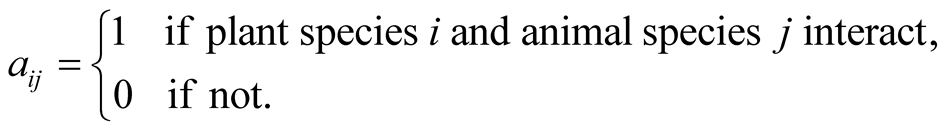 (1)
(1)
This is the object that represents the qualitative information in the BIN. An illustrative example of the bipartite networks is given in Figure 1. It has dimensions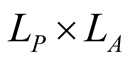 , where
, where  and
and 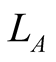 are the numbers of plant and animal species in the community. We can project the information in the matrix onto connectivity vectors of plants,
are the numbers of plant and animal species in the community. We can project the information in the matrix onto connectivity vectors of plants,  , and animals,
, and animals, 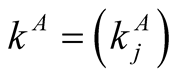 , by
, by
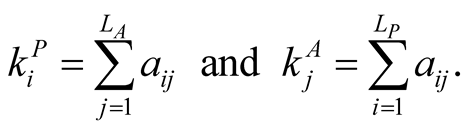 (2)
(2)
The quantity  gives the number of animal species that interact with plant species i, and
gives the number of animal species that interact with plant species i, and  the number of plant species that interact with animal species j. Finally we define N, the total number of interactions in the network or the total number of occupied sites in the matrix, by
the number of plant species that interact with animal species j. Finally we define N, the total number of interactions in the network or the total number of occupied sites in the matrix, by
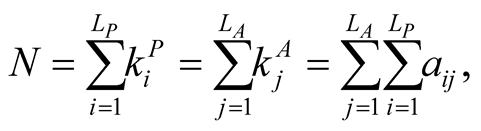 (3)
(3)
and the density 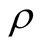 of occupied sites by
of occupied sites by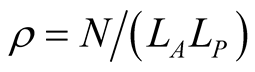 .
.
2.1. Connectivity Asymmetry for Qualitative BINs
Let us define the 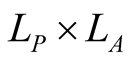 connectivity asymmetry matrix
connectivity asymmetry matrix 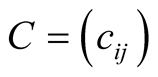 between plant i and animal j by
between plant i and animal j by
 (4)
(4)
(An alternative definition, 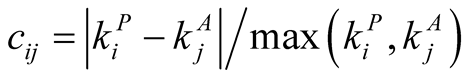 , gives similar results but is less mathematically tractable. Others [16] have omitted the modulus signs in defining similar quantities, but we are only interested in the absolute value of the difference between the connectivities of plant species i and animal species j.) Note that
, gives similar results but is less mathematically tractable. Others [16] have omitted the modulus signs in defining similar quantities, but we are only interested in the absolute value of the difference between the connectivities of plant species i and animal species j.) Note that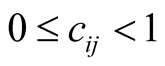 , and
, and 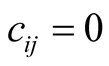 in the symmetric case where the plant and the animal have equal connectivity, while maximal asymmetry is achieved when maximally specialist plants
in the symmetric case where the plant and the animal have equal connectivity, while maximal asymmetry is achieved when maximally specialist plants 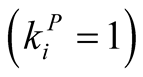 interact with maximally generalist
interact with maximally generalist
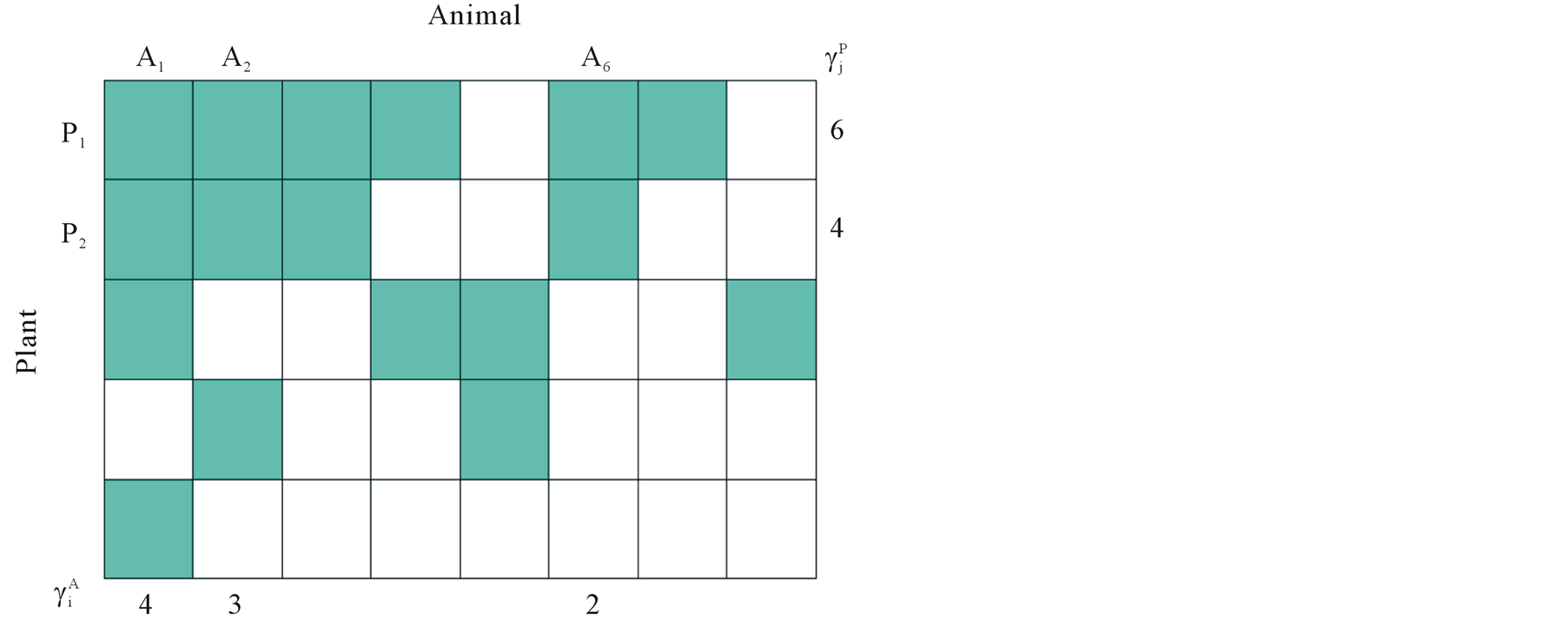
Figure 1. An illustration of a typical adjacency matrix. The shaded boxes indicate interaction between plant and animal species. We highlighted row and columns of plant P2 and animal A6. The dependence of these species is  and
and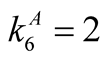 . The asymmetry between these particular plant and animal species is
. The asymmetry between these particular plant and animal species is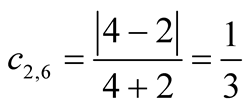 .
.
animals , or maximally specialist animals
, or maximally specialist animals 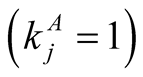 interact with maximally generalist plants
interact with maximally generalist plants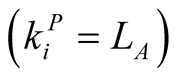 . In these cases
. In these cases 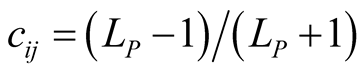 or
or , which tend to 1 as
, which tend to 1 as 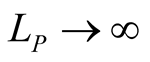 or
or 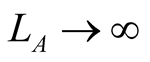 respectively.
respectively.
The global connectivity asymmetry 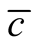 of a BIN is given by averaging
of a BIN is given by averaging 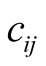 over all the occupied sites of the matrix,
over all the occupied sites of the matrix,
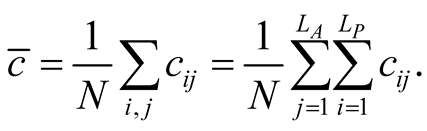 (5)
(5)
Note that, despite a claim to the contrary for a similar index [16] , this is not well approximated by 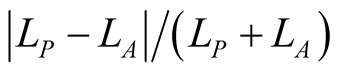 . In particular,
. In particular, 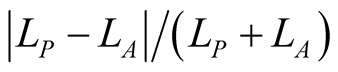 is zero if
is zero if , and we shall see later that
, and we shall see later that 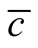 does not share this property.
does not share this property.
It is interesting to note that, by definition, 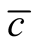 is a quantity that depends only on the total number of interactions of species,
is a quantity that depends only on the total number of interactions of species, 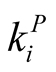 for plants i and
for plants i and 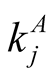 for animals j. The number of interactions, in its turn, is not affected by permutations of lines or columns in the matrix. In this way
for animals j. The number of interactions, in its turn, is not affected by permutations of lines or columns in the matrix. In this way 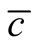 does not require any matrix-packing procedure that is commonly used in the estimation of nestedness [11] .
does not require any matrix-packing procedure that is commonly used in the estimation of nestedness [11] .
2.2. Dependence and Connectivity Asymmetry
The dependence 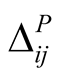 of a plant species i on an animal species j is a measure of how much plant species i depends on animal species j, and is defined for a qualitative network by
of a plant species i on an animal species j is a measure of how much plant species i depends on animal species j, and is defined for a qualitative network by
 (6)
(6)
The 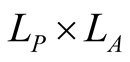 dependence matrix
dependence matrix 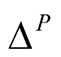 for plants is defined by
for plants is defined by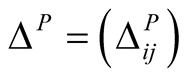 . In this way, a maximally specialist plant species i that interacts with just one animal species j has a maximal dependence
. In this way, a maximally specialist plant species i that interacts with just one animal species j has a maximal dependence  on that species, while a maximally generalist plant species i that interacts with all
on that species, while a maximally generalist plant species i that interacts with all 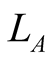 animal species has minimal dependence
animal species has minimal dependence 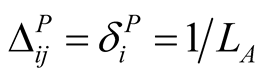 for every animal species j, with
for every animal species j, with 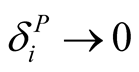 as
as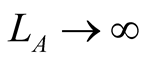 . Similarly, the dependence
. Similarly, the dependence 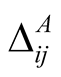 of an animal species j on a plant species i is defined by
of an animal species j on a plant species i is defined by
 (7)
(7)
and the 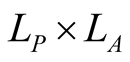 dependence matrix
dependence matrix 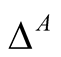 for animals is defined by
for animals is defined by . (Note that we retain the convention of using the rows of a matrix for plants and the columns for animals, so that the second index in
. (Note that we retain the convention of using the rows of a matrix for plants and the columns for animals, so that the second index in  refers to the dependent species.) Just as for plants, a maximally specialist animal species has dependence 1 on the single plant species that it interacts with, while a maximally generalist animal species has dependence
refers to the dependent species.) Just as for plants, a maximally specialist animal species has dependence 1 on the single plant species that it interacts with, while a maximally generalist animal species has dependence 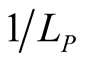 on each and every plant species.
on each and every plant species.
The dependence asymmetry 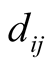 between animal species i and plant j is a quantity that express the difference between the two dependences, and is given by
between animal species i and plant j is a quantity that express the difference between the two dependences, and is given by
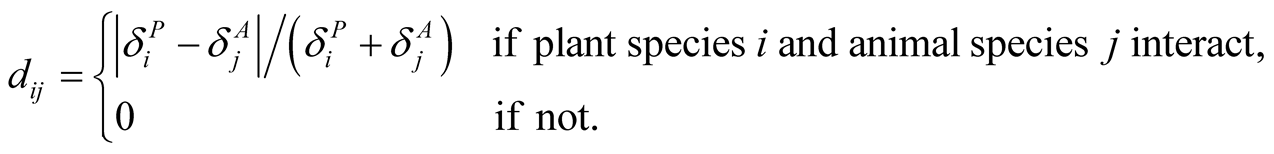 (8)
(8)
The 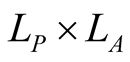 dependence asymmetry matrix is given by
dependence asymmetry matrix is given by . (Just as for connectivity asymmetry, the alternative definition
. (Just as for connectivity asymmetry, the alternative definition 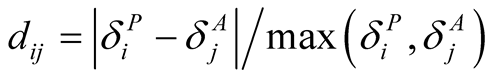 gives similar results but is less mathematically tractable. This alternative definition is essentially that of [9] , but adapted to a qualitative network.) Note that
gives similar results but is less mathematically tractable. This alternative definition is essentially that of [9] , but adapted to a qualitative network.) Note that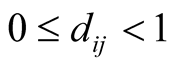 . Moreover,
. Moreover,  , since
, since 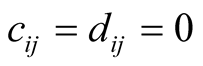 if plant species i does not interact with animal species j, while if there is an interaction,
if plant species i does not interact with animal species j, while if there is an interaction,
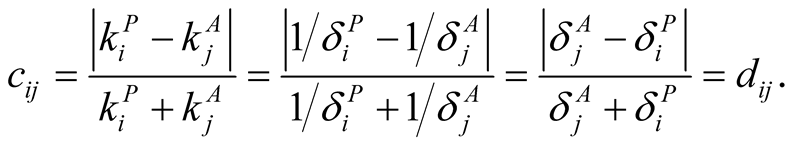 (9)
(9)
Dependence and connectivity asymmetry for qualitative networks are essentially the same concept, as has been pointed out in [3] .
2.3. The Number of Nested Patterns
The number of nested patterns can be estimated analytically or algorithmically. For sake of simplicity we restrict our analysis to the case of a square matrix of size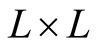 . In the first step of the construction of an artificial nested pattern we have to be sure that all species have at least one link. To fulfil this statement we set in the matrix an outer shell of occupied elements; this procedure may be visualised in the set of Figure 2. In this set the empty sites are white and the occupied sets are grey—the clear grey sites are the outer shell. The number of elements in the outer shell,
. In the first step of the construction of an artificial nested pattern we have to be sure that all species have at least one link. To fulfil this statement we set in the matrix an outer shell of occupied elements; this procedure may be visualised in the set of Figure 2. In this set the empty sites are white and the occupied sets are grey—the clear grey sites are the outer shell. The number of elements in the outer shell, 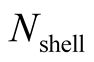 , is given by
, is given by .
.
Recall that N is the total number of occupied sites in the matrix, and define 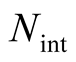 to be the number of elements of the matrix that do not belong to the external shell; in this way
to be the number of elements of the matrix that do not belong to the external shell; in this way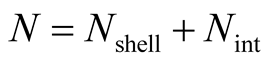 . In Figure 2 the internal elements are shown in a dark grey tone. To compute the total number of different perfectly nested patterns,
. In Figure 2 the internal elements are shown in a dark grey tone. To compute the total number of different perfectly nested patterns, 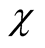 , we start with the simplest case where
, we start with the simplest case where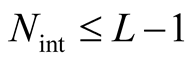 . To illustrate this case we show in Figure 2 five matrices with
. To illustrate this case we show in Figure 2 five matrices with 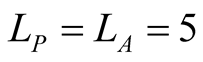 and
and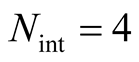 ; the nested matrices of this set of figures correspond to all possible arrangements of matrices with
; the nested matrices of this set of figures correspond to all possible arrangements of matrices with  and no gaps in their arrangement. Indeed, the arrangement of inner elements follows a partition of a positive integer, in this case, the partition of 4. In number theory, a partition of a positive integer N counts the total number of ways that N may be written as a sum of positive integers. The number of partitions of N is given by the partition function
and no gaps in their arrangement. Indeed, the arrangement of inner elements follows a partition of a positive integer, in this case, the partition of 4. In number theory, a partition of a positive integer N counts the total number of ways that N may be written as a sum of positive integers. The number of partitions of N is given by the partition function 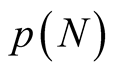 [17] .
[17] .
In Figure 3 we show 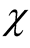 versus the number of occupied sites N. The main function depicted in the graphic is the partition function
versus the number of occupied sites N. The main function depicted in the graphic is the partition function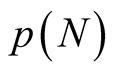 . In the case that
. In the case that 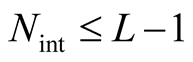 the number of distinct nested patterns is equal to
the number of distinct nested patterns is equal to  itself. For
itself. For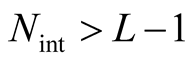 , the number of distinct nested patterns is smaller than
, the number of distinct nested patterns is smaller than 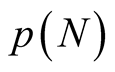 because partitions of N that extend beyond the length of the square (vertically or horizontally) are not allowed. A generic expression of the
because partitions of N that extend beyond the length of the square (vertically or horizontally) are not allowed. A generic expression of the 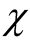 is given by
is given by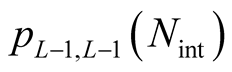 , the number of partitions of Nint into a sum of no more than
, the number of partitions of Nint into a sum of no more than 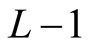 integers with no term greater than
integers with no term greater than 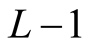 in the sum. The curve of
in the sum. The curve of 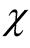 is symmetric relative to
is symmetric relative to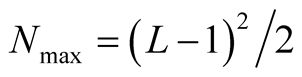 ;
;
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e)
Figure 2. A set of all possible nested patterns for LP = LA = 5 and N = 13 occupied elements. We can split any of these figures into a outer shell structure of 2 × 5 − 1 = 9 elements and 4 internal occupied sites. For this example the complete set of five nested patterns forms a Ferrers diagram.
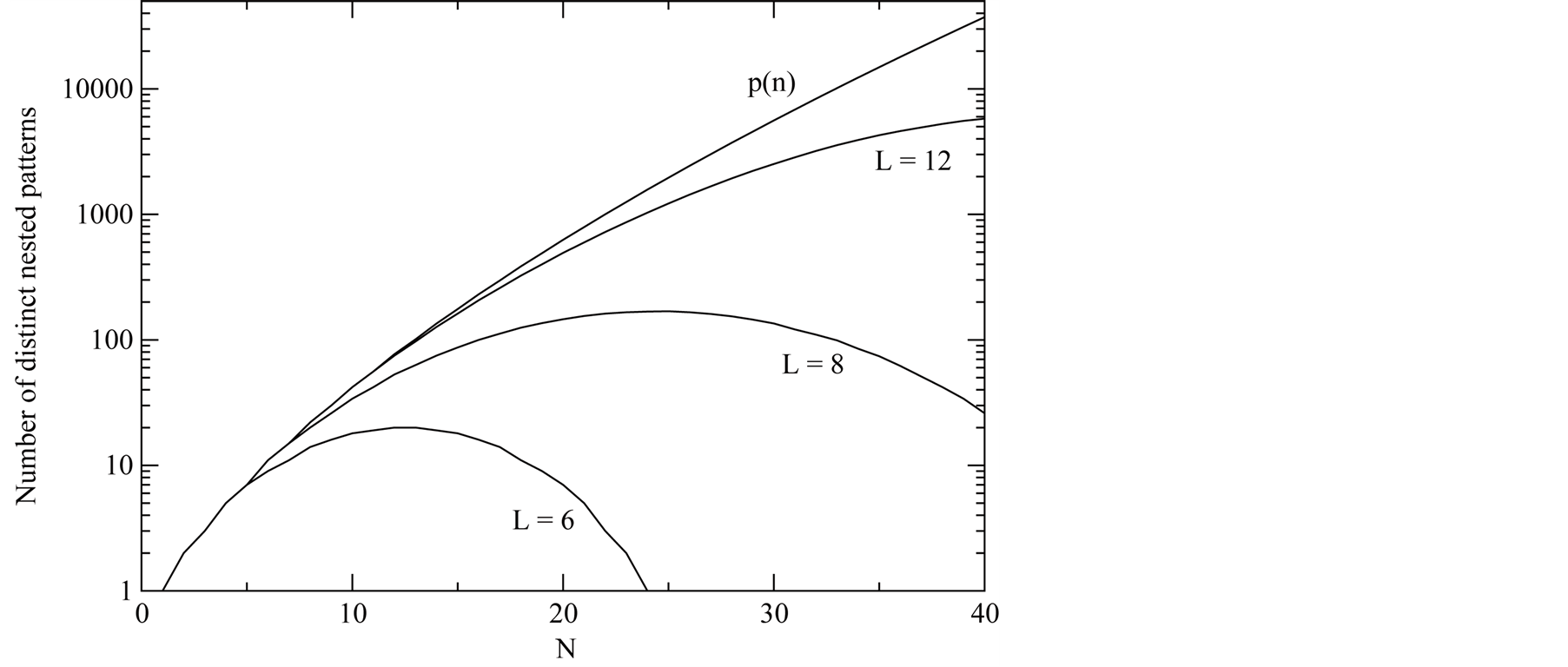
Figure 3. A curve of the total number of different perfectly nested patterns, χ, for several cases. The partition function p (N) is the upper boundary curve of χ. We illustrate the cases of L = 6, 8 and 12; for these cases the χ depart from the curve because a finite lattice cannot effect all the integer partitions.
indeed, for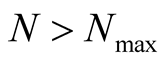 ,
, 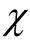 becomes the same as another related quantity, the number of different anti-nested patterns, or nested patterns formed by empty sites instead of occupied ones.
becomes the same as another related quantity, the number of different anti-nested patterns, or nested patterns formed by empty sites instead of occupied ones.
An asymptotic expression for 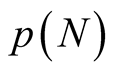 in the limit as
in the limit as 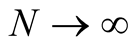 is given [18] by
is given [18] by
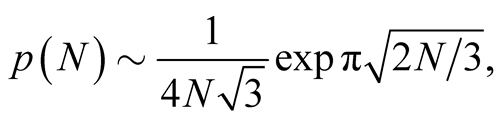 (10)
(10)
and the modified partition function  has similar asymptotic behaviour. In this equation the exponential term dominates the expression for large N. The conclusion we take from this expression is that for a large number of interactions, N, the number of possible nested arrangements grows exponentially. Such a property seems not to encourage the use of nestedness to produce characteristic indices of BINs, and we discuss this point in the conclusion.
has similar asymptotic behaviour. In this equation the exponential term dominates the expression for large N. The conclusion we take from this expression is that for a large number of interactions, N, the number of possible nested arrangements grows exponentially. Such a property seems not to encourage the use of nestedness to produce characteristic indices of BINs, and we discuss this point in the conclusion.
2.4. Asymmetry Distribution among Nested Patterns
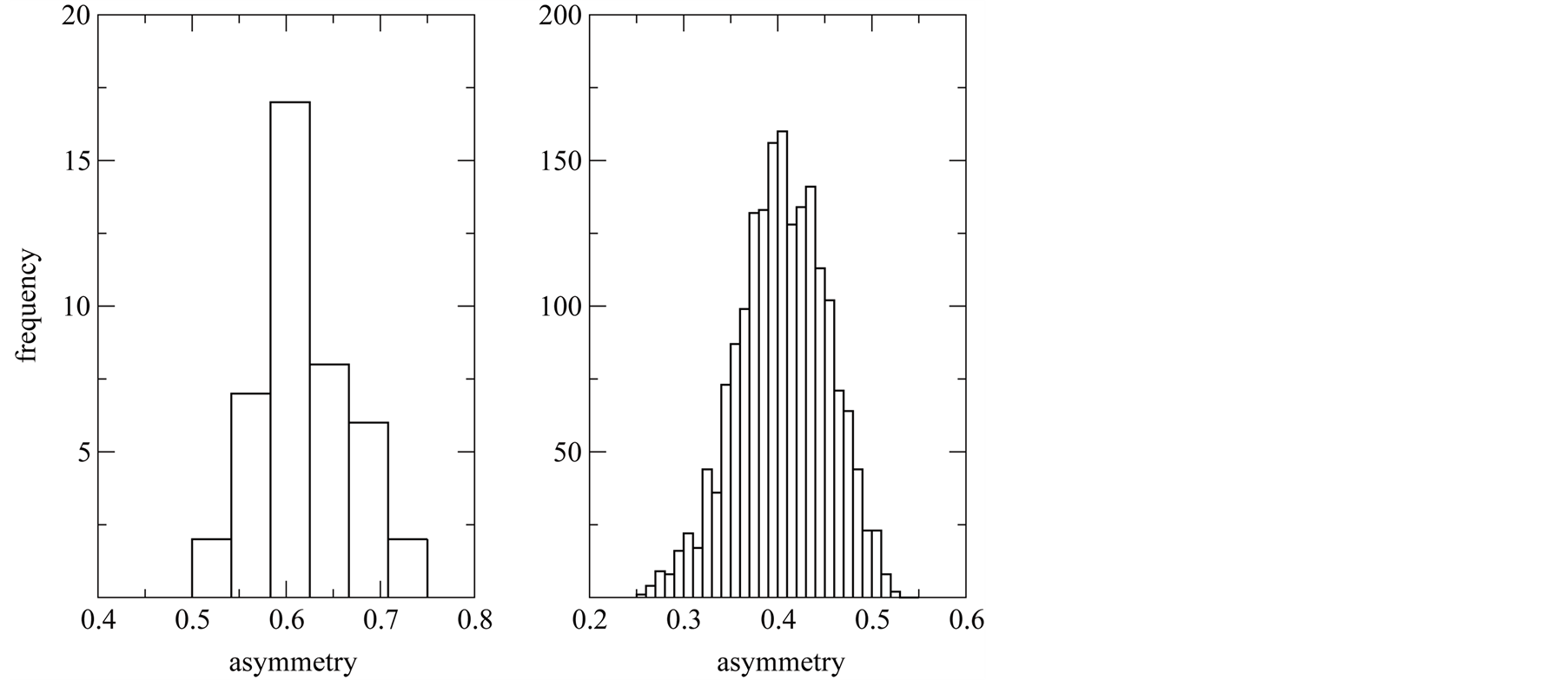
To understand how connectivity or dependence asymmetry and nestedness are related we plot histograms of  for all the multiplicity of nested patterns. This procedure enables us to grasp the differences in
for all the multiplicity of nested patterns. This procedure enables us to grasp the differences in 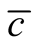 that are inside the set of possible nested arrangements for a given L and N. Figure 4 shows, for L = 11, two distinct cases: in (a) the occupation is low,
that are inside the set of possible nested arrangements for a given L and N. Figure 4 shows, for L = 11, two distinct cases: in (a) the occupation is low, 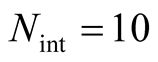 , and in (b) it is high,
, and in (b) it is high,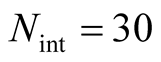 . As
. As 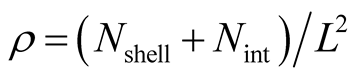 we have
we have 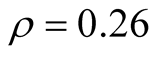 in (a) and
in (a) and 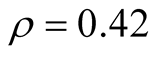 in (b). Although the two pictures show similar distribution patterns, we highlight two differences between them. The first is that values of asymmetry are larger for smaller
in (b). Although the two pictures show similar distribution patterns, we highlight two differences between them. The first is that values of asymmetry are larger for smaller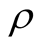 , because generalists in this case are connected largely to specialists, producing sites of high asymmetry. On the other hand, for high
, because generalists in this case are connected largely to specialists, producing sites of high asymmetry. On the other hand, for high 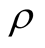 the matrix is densely occupied and specialists become scarce, decreasing the average asymmetry of the sites. The second point to which we call attention is that
the matrix is densely occupied and specialists become scarce, decreasing the average asymmetry of the sites. The second point to which we call attention is that 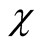 is much larger for high
is much larger for high , a result that comes directly from Figure 3 or, in a similar way, from Equation (10).
, a result that comes directly from Figure 3 or, in a similar way, from Equation (10).
We now stress the cases of patterns of maximal and minimal 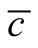 among the set of all different nested patterns. The point here is to understand the configurations that produce the extremes of
among the set of all different nested patterns. The point here is to understand the configurations that produce the extremes of 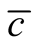 in the histograms of Figure 4. This question is important because we can understand the appearance of matrices of high and low asymmetry. In Figure 5 we show, for a square matrix with
in the histograms of Figure 4. This question is important because we can understand the appearance of matrices of high and low asymmetry. In Figure 5 we show, for a square matrix with 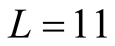 and
and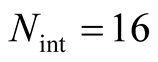 , the matrices of lowest
, the matrices of lowest 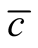 in (a) and of highest
in (a) and of highest 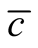 in (c). The case (c) is not unique, since a reflected figure along the diagonal of the square has the same asymmetry. The case of minimal
in (c). The case (c) is not unique, since a reflected figure along the diagonal of the square has the same asymmetry. The case of minimal 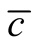 is easy to understand: all elements of the internal square have
is easy to understand: all elements of the internal square have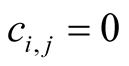 , since
, since 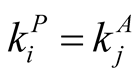 for all i and j, which produces an arrangement of very low
for all i and j, which produces an arrangement of very low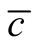 . On the other side, the maximum
. On the other side, the maximum 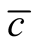 is formed by a combination of the maximum number of generalists that can coexist with the
is formed by a combination of the maximum number of generalists that can coexist with the
 (a) (b)
(a) (b)
Figure 4. Two histograms illustrating the distributions of asymmetry, where L = 11 and the number of occupied sites is (a) low, Nint = 10, and (b) high, Nint = 30.
 (a)
(a) (b)
(b) (c)
(c)
Figure 5. The complete nested matrices illustrating to three cases of dependence asymmetry for a same : in (a) the minimal
: in (a) the minimal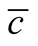 , in (b) the average
, in (b) the average 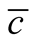 and in (c) the maximal
and in (c) the maximal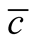 . We use in this simulation
. We use in this simulation 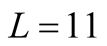 and
and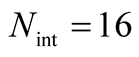 . The case of minimal
. The case of minimal  is characterised by a solid modular structure while the maximal
is characterised by a solid modular structure while the maximal 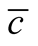 is formed by two additional generalists. The typical case of a nested pattern is depicted in (b), the average
is formed by two additional generalists. The typical case of a nested pattern is depicted in (b), the average 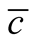 among the ensemble of nested patterns.
among the ensemble of nested patterns.
maximum number of specialists; the consequence of this choice is the complete exclusion of species that are neither maximally generalists nor specialists. We plot also in Figure 5(b) the median of histogram. This pattern resembles a typical nested pattern, and we stress this point in the discussion.
3. Discussion and Final Remarks
In this work we compare two concepts that are used to investigate interaction networks: nestedness and connectivity or dependence asymmetry. Our strategy to deal with this problem is to analyse the total set of perfectly nested matrices, for a given size and occupancy, and to compute 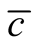 for all of them. The result of this analysis is summarised in Figure 4 and Figure 5. We conclude that inside the ensemble of nested patterns there is a range of matrices of diverse
for all of them. The result of this analysis is summarised in Figure 4 and Figure 5. We conclude that inside the ensemble of nested patterns there is a range of matrices of diverse . At one extreme of the range we have symmetric patterns characterised by the presence of many sites of zero asymmetry that form a core of species with the same connectivity that interact amongst themselves as in a modular structure. In the opposite extreme, the case of maximal asymmetry corresponds to a situation where we have only generalists and specialists with the same number of interacting partners. It is interesting to note that the pictorial examples of nested patterns shown in scientific articles [12] [19] show an intermediate
. At one extreme of the range we have symmetric patterns characterised by the presence of many sites of zero asymmetry that form a core of species with the same connectivity that interact amongst themselves as in a modular structure. In the opposite extreme, the case of maximal asymmetry corresponds to a situation where we have only generalists and specialists with the same number of interacting partners. It is interesting to note that the pictorial examples of nested patterns shown in scientific articles [12] [19] show an intermediate  between these two extreme cases.
between these two extreme cases.
We recall three aspects of a nested pattern that we have outlined in the introduction: a) a core of generalists that interact with another generalist; b) many generalists that interact with specialists; and c) an absence of interactions between specialists. A generalist connected to many specialists gives origin to sites of high asymmetry, and an interaction of a specialist with another specialist produces sites of zero asymmetry; the absence of this pattern in nested networks also increases the asymmetry. In this way, cases (b) and (c) are typical of networks with high asymmetry. On the one hand, a core of generalists interacting with generalists leads to sites of low asymmetry, which contribute to decreasing the asymmetry. This picture agrees with the last sentence of the previous paragraph: the stereotype of an optimal nested pattern is something “in between” two extremes of asymmetry dependence. We remark that the ensemble of perfectly nested patterns does not necessarily fulfill conditions (a) and (b). Indeed, inside the spectrum of perfectly nested patterns, the case of minimal 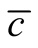 does not fulfil condition (b) and the case of maximal
does not fulfil condition (b) and the case of maximal 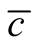 does not follow condition (a). However, the nested patterns around the peak of distribution of
does not follow condition (a). However, the nested patterns around the peak of distribution of 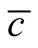 follows conditions (a), (b) and (c), in agreement with the ecological concept of nestedness [12] [13] [19] .
follows conditions (a), (b) and (c), in agreement with the ecological concept of nestedness [12] [13] [19] .
In this work we call attention to one aspect that has not been stressed in the literature [11] [19] . The nested patterns have an internal multiplicity of states; and furthermore, the number of perfectly nested patterns grows exponentially with the number of occupied sites, Equation (10). However, despite the fact that perfectly nested patterns are asympotically like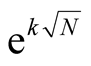 , the total number of patterns is asympotically like
, the total number of patterns is asympotically like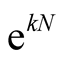 . In this way the number of perfectly nested structures is a very small fraction of the total number of patterns. This justifies, in a statistical way, the use of nested patterns for the construction of indices. In addition, the use of a nestedness index usually occurs in comparison with an ensemble of random matrices that have the same distribution of
. In this way the number of perfectly nested structures is a very small fraction of the total number of patterns. This justifies, in a statistical way, the use of nested patterns for the construction of indices. In addition, the use of a nestedness index usually occurs in comparison with an ensemble of random matrices that have the same distribution of  and
and 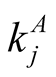 [7] [11] [20] . Such a procedure, known as the R3 null model, restricts strongly the number of nested structures with a given N and enables a reasonable use of a nestedness index. For the case of perfectly nested pattern there is just one pattern for fixed
[7] [11] [20] . Such a procedure, known as the R3 null model, restricts strongly the number of nested structures with a given N and enables a reasonable use of a nestedness index. For the case of perfectly nested pattern there is just one pattern for fixed 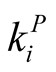 and
and , but for a generic case this point is unclear. We note that there is an analytic result in the literature that can be used to clarify this point. In the work [21] there is a proof that the nestedness index
, but for a generic case this point is unclear. We note that there is an analytic result in the literature that can be used to clarify this point. In the work [21] there is a proof that the nestedness index 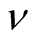 depends only on
depends only on 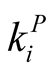 and
and  to be calculated; however, there is not yet a well established relation of
to be calculated; however, there is not yet a well established relation of 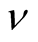 with other nestedness indices like the NODF [22] or the Temperature of Atmar [23] .
with other nestedness indices like the NODF [22] or the Temperature of Atmar [23] .
Connectivity or dependence asymmetry seems to be a good candidate to characterise qualitative BINs, and we give at least two reasons for that. It is easy to compute because it is not necessary to perform a matrix-packing procedure, besides we compute 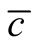 by counting
by counting  over matrix elements, which can be done in one line of a program in R. The second point is that asymmetry has a direct ecological interpretation: it computes the imbalance of species connectivities in the network. On the other side, the difficulty of using
over matrix elements, which can be done in one line of a program in R. The second point is that asymmetry has a direct ecological interpretation: it computes the imbalance of species connectivities in the network. On the other side, the difficulty of using 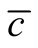 as an index is that it should be properly normalised or exhaustively compared with null models [11] [24] . Without a comprehensive test of
as an index is that it should be properly normalised or exhaustively compared with null models [11] [24] . Without a comprehensive test of 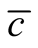 against matrix sizes and occupancy, it is not expected that
against matrix sizes and occupancy, it is not expected that 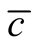 could be used to compare matrices of different L and
could be used to compare matrices of different L and . At this moment we are working on a well normalised asymmetry index that we intend to use to distinguish antagonist from mutualist networks.
. At this moment we are working on a well normalised asymmetry index that we intend to use to distinguish antagonist from mutualist networks.
Acknowledgements
Financial support to Gilberto Corso from CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) is acknowledged.
References
- Bascompte, J. and Jordano, P. (2013) Mutualistic Networks, Princeton University Press, Princeton.
- Fointaine, C. (2013) Abundant Equals Nested. Nature, 500, 411-412. http://dx.doi.org/10.1038/500411a
- Dormann, C.F., Fründ, J., Blüthgen, N. and Gruber, B. (2009) Indices, Graphs and Null Models: Analyzing Bipartite Ecological Networks. The Open Journal of Ecology, 2, 7-24. http://dx.doi.org/10.2174/1874213000902010007
- Ings, T.C., Montoya, J.M., Bascompte, J., Blüthgen, N., Brown, L., Dormann, C.F., et al. (2009) Ecological Networks—Beyond Food Webs. Journal of Animal Ecology, 78, 253-269. http://dx.doi.org/10.1111/j.1365-2656.2008.01460.x
- Bascompte, J. (2009) Disentangling the Web of Life. Science, 325, 416-419. http://dx.doi.org/ 10.1126/science.1170749
- Suweis, S., Simini, F., Banavar, J.R. and Maritan, A. (2013) Emergence of Structural and Dynamics Properties of Ecological Mutualistic Networks. Nature, 500, 449-452. http://dx.doi.org/10.1038/nature12438
- Thébault, E. and Fontaine, C. (2010) Stability of Ecological Communities and the Architecture of Mutualistic and Trophic Networks. Science, 329, 853-856. http://dx.doi.org/10.1126/science.1188321
- Vázquez, D.P. and Aizen, M.A. (2004) Asymmetric Specialisation: A Pervasive Feature of Plant-Pollinator Interactions. Ecology, 85, 1251-1257. http://dx.doi.org/10.1890/03-3112
- Bascompte, J., Jordano, P. and Olesen, J.M. (2006) Asymmetric Coevolutionary Networks Facilitate Biodiversity Maintenance. Science, 312, 431-433. http://dx.doi.org/10.1126/science.1123412
- Blüthgen, N., Menzel, F. and Blüthgen, N. (2006) Measuring Specialization in Species Interaction Networks. BMC Ecology, 6, 9. http://dx.doi.org/10.1186/1472-6785-6-9
- Ulrich, W., Almeida-Neto, M. and Gotelli, N.J. (2009) A Consumer’s Guide to Nestedness Analysis. Oikos, 118, 3-17.http://dx.doi.org/10.1111/j.1600-0706.2008.17053.x
- Bascompte, J., Jordano, P, Melián, C.J. and Olesen, J.M. (2003) The Nested Assembly of Plant-Animal Mutualistic Networks. Proceedings of the National Academy of Sciences of the United States of America, 100, 9383-9387. http://dx.doi.org/10.1073/pnas.1633576100
- Guimaraes Jr., P.R., Rico-Gray, V., dos Reis, S.F. and Thompson, J.N. (2006) Asymmetries in Specialization in Ant Plant Mutualistic Networks. Proceedings of the Royal Society B: Biological Sciences, 273, 2041-2047.
- Araujo, A.I.L., Corso, G., Almeida, A.M. and Lewinsohn, T.M. (2010) An Analytic Approach to Nestedness Index of Bipartite Networks. Physica A: Statistical Mechanics and Its Applications, 389, 1405-1411. http://dx.doi.org/10.1016/j.physa.2009.11.030
- Brualdi, R.A. and Sanderson, J.G. (1999) Nested Species Subsets, Gaps, and Discrepancy. Oecologia, 119, 256-264.http://dx.doi.org/10.1007/s004420050784
- Blüthgen, N. (2010) Why Network Analysis Is Often Disconnected from Community Ecology: A Critique and An Eco logist’s Guide. Basic and Applied Ecology, 11, 185-195. http://dx.doi.org/10.1016/j.baae.2010.01.001
- Hardy, G.H. and Wright, E.M. (1938) An Introduction to the Theory of Numbers. Oxford University Press, Oxford.
- Hardy, G.H. and Ramanujan, S. (1918) Asymptotic Formulae in Combinatory Analysis. Proceedings of the London Mathematical Society, 17, 75-115. http://dx.doi.org/10.1112/plms/s2-17.1.75
- Lewinsohn, T.M., Prado, P.I., Jordano, P., Bascompte, J. and Olesen, J.M. (2006) Structure in Plant-Animal Interaction Assemblages. Oikos, 113, 174. http://dx.doi.org/10.1111/j.0030-1299.2006.14583.x
- Fortuna, M.A., Stouffer, D.B., Olesen, J.M., Jordano, P., Mouillot, D., Krasnov, B.R., et al. (2010) Nestedness versus Modularity in Ecological Networks: Two Sides of the Same Coin? Journal of Animal Ecology, 79, 811-817.
- Corso, G., Araujo, A.I.L. and Almeida, A.M. (2011) Connectivity and Nestedness in Bipartite Networks from Community Ecology. Journal of Physics: Conference Series, 285, Article ID: 012009.
- Almeida-Neto, M., Guimaraes, P.R. and Lewinsohn, T.M. (2007) On Nestedness Analyses: Rethinking Matrix Temperature and Anti-Nestedness. Oikos, 116, 716-722. http://dx.doi.org/10.1111/j.0030-1299.2007.15803.x
- Patterson, B.D. and Atmar, W. (1986) Nested Subsets and the Structure of Insular Mammalian Faunas and Archipelagos. Biological Journal of the Linnean Society, 28, 65-82. http://dx.doi.org/10.1111/j.1095-8312.1986.tb01749.x
- Gotelli, N.J. and Graves, G.R. (1996) Null Models in Ecology. Smithsonian Institution Press, Washington DC.
NOTES

*Corresponding author.

