Open Journal of Molecular and Integrative Physiology
Vol.07 No.03(2017), Article ID:78609,6 pages
10.4236/ojmip.2017.73003
Dinosaur Dynamics in an Integrative Model for Rotating Rocks and Deformable Bodies
Lena J-T Strömberg
Previously Sigma, epsilon engrg, and Dep of Solid Mech, Royal Inst of Techn, KTH, Stockholm, Sweden

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 15, 2017; Accepted: August 19, 2017; Published: August 22, 2017
ABSTRACT
Present long range interactions for signals, as well as large scale rare phenomena at Earthquakes are subjects of wave dynamics with large impact. Here, that will be addressed in a general (science fiction) format. The method used is based on energy balance for a continuum and kinematics of noncircular orbits, nco. Released vortex formation in a process invoking escape velocity for beamed up Dinosaurs, is modeled with fluid dynamics of a Helix. It is found that elasticity in terms of volumetric changes and vorticities interact giving large velocities and interchange of potential and kinetic energies. The model is an example of atmosphere integrative physiology.
Keywords:
Angular Velocity, Vorticity, Eddy, Fluid Dynamics, Helix, Noncircular Orbit, Nco, Energy Balance, Density, Integrative Physiology, Dinosaur, Beam up

1. Introduction
With the 3 pictures from NASA, in Figure 1, as the point of departure, we shall discuss models invoking possible ancient texture and life in the close atmosphere.
Nowadays at day time, there are clouds and wind dynamics, together with all the new IT-signals. These are small scale, and present in an enormous multitude beyond reach. Several isolated phenomena and also complex flows, are covered with different models and simulations. In the present paper, we will consider few assumptions for a spiral shaped motion, such that dynamics enter due to interaction of whirls and volumetric changes of space. The results display as formulas for the motion. Such formats have significance in many applications, both on large and small scales. However, as is pointed out, when comparing with



Figure 1. NASA images from space.
experimental results, also interpretations in terms of fractals and discrete point solutions sometimes needs to be invoked. Realizing this provides the novelty of the paper together with the exact results, based on a relatively small initial model.
At night, several sights are found by amateur astronomers e.g. black holes in between two stars and a light spot with an aura. Here, a strange interaction in the sky will be elaborated: Since the Dinosaurs were large, rocky in texture and with ability to fly, these could have been involved in possible past formations in the sky.
The scenario is partly outlined by Mr J Sullivan c.f. [1] : In history, at occasions, the atmosphere may have been different in terms of texture and density. For about 300 million years ago, i.e. nearly the time of Dinosaurs, massive meteorites hit the Earth, and possibly there were also large-scale wave activity in the sky.
First, we will revisit the wave dynamics proposed in [1] . Then a new formation will be derived, given as a Helix whirl at Earth, from which matter is thrown up in the atmosphere.
2. A Past Dense Atmosphere
Although, the elastic waves without scattering and damping derived in [1] , is ideal and not entirely realistic, we shall export the idea into an initial upward velocity. Consider the elastic surface wave in [1] propagating on Earth “eating” Dinosaurs and other matter. A change of shape into a larger curvature and disintegration of particles into a quantum mass gives a tangent velocity infinitely large. Comparing with whirlwinds acting nowadays, they have capacity of moving cars and roofs. The suggestion above is the same, up-scaled.
3. Background for a Helix
Within electromagnetism EM [2] [3] [4] , a Helix formation is an ideal model for ion beams inside a cyclotron accelerator. Here, we will assume energy from kinematics of whirls together with density variations. A link to magnetism is difficult to provide since rotations of stones alone are not subjected to Lorentz forces. If occuring in the Earth magnetic field and the matter is ferrous, a coupling is possible.
This Helix flow will be analysed by exact analytic methods. Since there is much work present in this area both exact and with CFD, initially we will provide a review reference.
Modeling of Whirls/Eddies with Continuum Dynamics
Computational fluid dynamics, CFD, with large eddy simulations, LES, is a powerful method, to simulate flows governed by some turbulence but also composed into other structures. In [2] , a wide range of examples are covered and visualized. The method appears to be applicable on both large and small scales, although usually whirls are considered as sublevels in a flow. For example Figure 2, given in [2] , provide beautiful solutions for the helix motion double curved, almost on a torus. As mentioned above, Helix flow occurs in cyclotron accelerators, but the solutions are not perfect and more complex than outlined in Wikipedia [3] .
LES refers to a discipline in fluid mechanics, where turbulent flow is consi
Figure 2. Long exposure photograph of several finite Stokes number particles moving in the laminar flow of a stirred tank. All particles start in a chaotic flow region but are eventually attracted into a KAM tube where they execute helical trajectories. From Wang, R. Stewart, and G. Metcalfe, 2016, “Visualization of the trapping of inertial particles in a laminar mixing tank”, Chem. Eng. Sci. 143, 99-104.
dered composed as spatial mean values with small variation. Issues in the modeling are to choose the scales and subdivisions, among many possible configurations and linearisation to achieve unique solutions. Sounding out the abbreviation, the word large probably refers to the number of eddies and the possibility of solving large problems. If referring to the grid size, such that entire whirls are not modeled in details, it is the opposite of Kolmogorov scale modeling. It could also point to other applications e.g. large scale astronomy. Here, we will consider eddies, on the meso-scale, consisting of a Dinosaur and rocks, mainly.
4. Equations for a Helix of Rocks and an Elastic Body
In what follows, the modeling is outlined. For a fluid with viscosity, continuum mechanics with thermodynamics and additional assumptions of heat capacity and heat flux gives an equation for the rate of energy
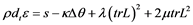 (1)
(1)
where, with usual notations; ,
,  , s,
, s,  ,
, 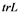 ,
, 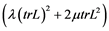 is the density, energy, heat radiation, temperature, trace of velocity gradient and internal friction in the viscous motion, and dt denotes entire time derivative. Here, we consider a flow where also vorticities w, such that L = D + W, D is symmetric and W = skew(L) = wx, where x is the cross product.
is the density, energy, heat radiation, temperature, trace of velocity gradient and internal friction in the viscous motion, and dt denotes entire time derivative. Here, we consider a flow where also vorticities w, such that L = D + W, D is symmetric and W = skew(L) = wx, where x is the cross product.
Continuity for mass reads 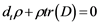 (2)
(2)
When the thermal part is self-balanced, (2) substituted in (1) gives
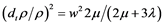 (3)
(3)
The change in density is due to elasticity for the Dinosaur, Figure 3, in con
Figure 3. Dinosaur physiology.
junction with structure interaction of the stones, and here, detailed models for that will be cast into a model for kinematics as in [5] .
Solutions for Angular Velocity
Next, evaluation of the densities is done to obtain the angular velocity components in the Helix.
Assume no explicit time dependency and the frame of a noncircular orbit nco [5] , i.e. with a harmonic velocity and frequency w0, L-frequency fw0, radius r0, eccentricity re.
Then, the derive of density can be evaluated such that 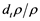 is either
is either
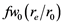 (4)
(4)
where the approximation  was used
was used
or, 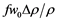 where a smeared density in the eccentricity zone was assumed and
where a smeared density in the eccentricity zone was assumed and  denotes this finite change in density.
denotes this finite change in density.
The angular velocity in the flow primarily concerns the xy-plane, Figure 4, such that w = wez. As seen in Figure 2, there are sublevels, and this could imply also super levels. The latter will be assumed in the present modeling, to give a tangent (upward) velocity vz at the boundary of the Helix that contributes to the escape velocity. Let wt denote this super level with a smaller vorticity and

With the density evaluation (4), above this gives

Remark: For the classical science fiction action “beamed up” in the tangential direction, the velocity v = wtR, R being some radius, is governing. In the present modeling, the radius R is arbitrary so in fact, energy or a flow criterion rules. However, for light, it is likely that v adjusts to a suitable value e.g. as from the Sun, reach a planet.
Figure 4. Helix with circular motion in-plane xy, and Radius r0.
5. Conclusion
Released vortex formation in a process invoking escape velocity for beamed up Dinosaurs, was modelled with fluid dynamics of a Helix. Modeling consists ofvolumetric changes and vorticities in interaction with density and an assumed noncircular orbit velocity. The concept provides an example of atmosphere integrative physiology. Other such not yet so exploited are human and animal interactions with the moon EM-signals and the Earth magnetic field.
Acknowledgements
To Dr Christian Baumgarten for telling about cyclotron accelerators, to astronomer Paul C Swift for sharing telescopic views of space, to Dr Benhmidene for valuable discussions on CFD and to Mr Adel Soualmia for information on space matter.
Cite this paper
J-T Strömberg, L. (2017) Dinosaur Dynamics in an Integrative Model for Rotating Rocks and Deformable Bodies. Open Journal of Molecular and Integrative Physiology, 7, 35-40. https://doi.org/10.4236/ojmip.2017.73003
References
- 1. Strömberg, L. and Sullivan, J.M. (2017) Concepts of Wave Amplification in Terms of Noncircular Orbits, and Its Impact on Dinosaurs’ Daily Life. Submitted to JPAR (Based on Techn. Report RG).
- 2. Hassan, A., et al. (2017) Frontiers of Chaotic Advection. Reviews of Modern Physics, 89, 025007.
https://doi.org/10.1103/RevModPhys.89.025007 - 3. Dr Christian Baumgarten, Personal Communication.
- 4. Dr Ronald Starke, Personal Communication on Ab initio Materials Physics and Microscopic Electromagnetism of Media and Dr Janusz Pudikiewicz on Vorticity and EM in Continuum Mechanics.
- 5. Strömberg, L. (2014) A Model for Non-Circular Orbits Derived from a Two-Step Linearisation of the Kepler Laws. Journal of Physics and Astronomy Research, 1, 013-014.




