Open Journal of Inorganic Chemistry
Vol.1 No.3(2011), Article ID:8153,6 pages DOI:10.4236/ojic.2011.13005
Magnetic analyses of isosceles tricobalt(II) complexes containing two types of octahedral high-spin cobalt(II) ions
![]()
1Department of Material and Biological Chemistry, Faculty of Science, Yamagata University, Kojirakawa, Japan;
2Department of Chemistry, The University of Sheffield, Sheffield, UK;
3Department of Chemistry, Faculty of Science, Kyushu University, Fukuoka, Japan.
Email: *saki@sci.kj.yamagata-u.ac.jp
Received 5 September 2011; revised 5 October 2011; accepted 20 October 2011.
Keywords: Tricobalt(II) Complex; Magnetic Properties; Spin-Orbit Coupling; Exchange Interaction
ABSTRACT
The observed magnetic data for two isosceles tricobalt(II) complexes have been successfully analyzed, considering the axial distortion around each cobalt(II) ion, the local spin-orbit coupling, the anisotropic exchange interactions, and the intermolecular exchange interactions. The complexes each contains two types of octahedral high-spin cobalt(II) ions (CoA and CoB) in the shape of an isosceles triangle (CoA1-CoB-CoA2), and the contribution of the orbital angular momentum is significant. The exchange interaction between the CoA and CoB ions is practically negligible (J = ~ 0), whereas the interaction between the CoA1 and CoA2 ions is ferromagnetic (J’ > 0) for both complexes.
1. INTRODUCTION
Magnetic analysis of multinuclear octahedral high-spin cobalt(II) complexes is a challenging subject because the orbital angular momentum makes the theoretical treatment difficult [1]. One of the most difficult points is that the local spin-orbit coupling is much larger than the exchange interactions [2]. Another difficult point is that the effect of local distortion is generally too large to be ignored, and that the anisotropic treatment is necessary [2,3].
For mononuclear octahedral high-spin cobalt(II) complexes, Lines [2] and Figgis [3] solved the problem, considering the axial distortion and spin-orbit coupling. For dinuclear complexes containing two equivalent octahedral high-spin cobalt(II) ions, Lines [4] developed a magnetic susceptibility equation for pure octahedral coordination geometries, and Sakiyama [5-10] developed susceptibility equations for distorted octahedral geometries considering the local axial distortion, local spin-orbit coupling, and isotropic/anisotropic exchange interaction. Palii et al. [11-13] derived analytical expressions for the components of the exchange parameter, the g-tensor, and the temperature independent paramagnetism (TIP), based on the application of irreducible tensor operator technique. Recently, Lloret et al. [14] proposed an empirical expression.
In spite of progress in the theoretical treatment of dinuclear high-spin cobalt(II) complexes, magnetic analysis of the trinuclear octahedral high-spin cobalt(II) complexes had not been successfully performed. In this study, a magnetic susceptibility equation was obtained for tricobalt(II) complexes in the shape of an isosceles triangle (CoA2-CoB-CoA2), considering local distortions, local spinorbit couplings, exchange interactions, and the intermolecular exchange interactions. Magnetic analyses were successfully performed for two trinuclear high-spin cobalt(II) complexes [Co3(L1)2(OCOMe)2(NCS)2] (1) and [Co3(L2)2(OCOMe)2(NCS)2] (2) (see Figure 1), whose crystal structures and magnetic data were previously reported [15].
2. EXPERIMENT
Magnetic Analysis
The entire calculation was performed on a Power Macintosh 7300/180 computer using the MagSaki(T) program

Figure 1. Chemical structures of L1– (R = C2H5) and L2– (R = n-C3H7).
developed by Sakiyama. Nine independent parameters κA,λA, ΔA, κB, λB, ΔB, J, J’, and θ were determined as described below. First, the susceptibility data above 50 K (or 100 K) were fitted using six local parameters κA, λA, ΔA, κB, λB, and ΔB, excluding the effect of exchange interactions between cobalt(II) ions. Secondly, fixing the six local parameters, the susceptibility data in the entire temperature range (2 - 300 K) were fitted to determine the remaining parameters J, J’, and θ, and finally all the parameters were optimized.
3. RESULTS AND DISCUSSION
3.1. Magnetic Susceptibility Equation for Isosceles Tricobalt(II) Complexes
In a trinuclear octahedral high-spin cobalt(II) complex, each cobalt(II) ion (O symmetry) has a local 4T1(4F) ground term, which is split into six Kramers doublets due to a spin-orbit coupling. When the cobalt(II) ion is axially distorted, the order of the six Kramers doublets changes; however, the second-lowest doublet is always more than 100 cm–1 higher than the lowest doublet [2]. Since the local spin-orbit coupling is much larger than the exchange interactions, the exchange interaction is effective only between the lowest doublets of cobalt(II) ions. Therefore, it is appropriate to assume that the exchange interaction causes no effect to the higher doublets [2,5].
Here we want to obtain a magnetic susceptibility equation for an isosceles tricobalt(II) core, as shown in
Figure 2. Full Hamiltonian is written as H = HLF + HLS+ HZE+ Hex, where HLF, HLS, HZE, and Hex are the ligand field term, LS coupling term, Zeeman term, and the exchange term of the Hamiltonian, respectively. The Hamiltonians HLF, HLS, and HZE are as follows: (see Equations (1)-(3))
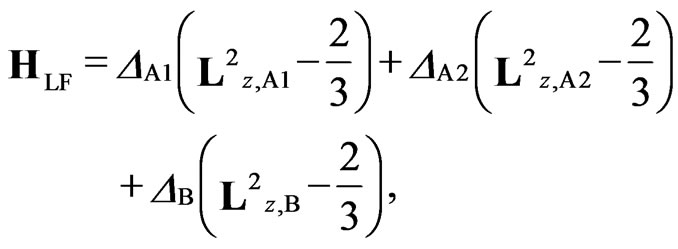 (1)
(1)
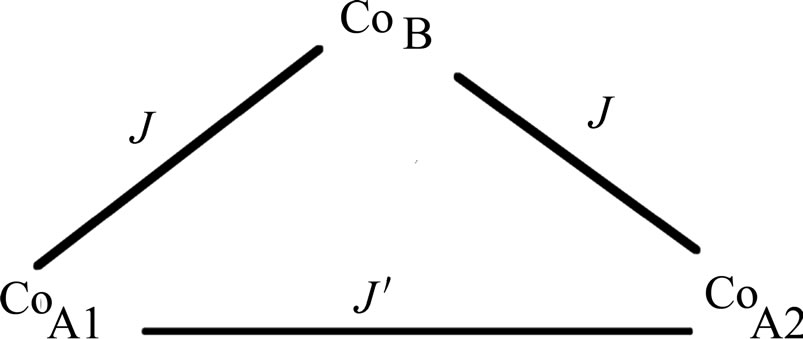
Figure 2. Isosceles tricobalt(II) core.
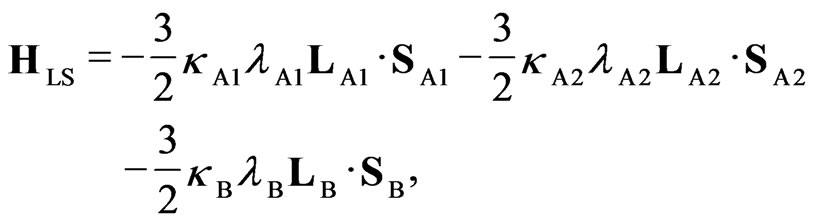 (2)
(2)
If we assume isotropic exchange interactions between local true spins (SA1 = SA2 = SB = 3/2), the exchange part of the Hamiltonian can be written as
 (4)
(4)
Since the local 4T1 ground term is split by spin-orbit coupling larger than the exchange interactions, the local effective spins (sA1 = sA2 = sB = 1/2) for the local lowest Kramers doublets are introduced [2,8].
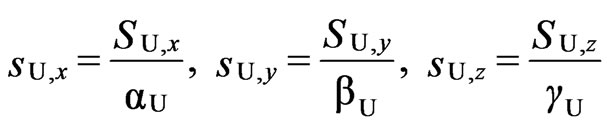
(U = A1, A2, and B) (5)
Assuming axial symmetry for local effective spins (βU = αU and sU,y = sU,x), the exchange Hamiltonian can be rewritten as
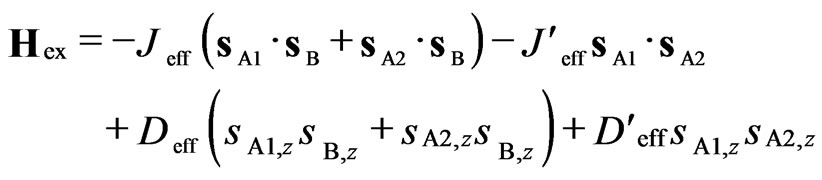 , (6)
, (6)
where and
and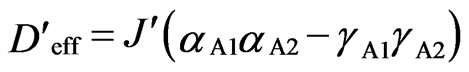 .
.
The coefficients αU and γU (U = A1, A2, and B) can be expressed by the local parameters κU, λU, and ΔU [2,8], where κU is the orbital reduction factor, λU is the spin-orbit coupling parameter, and ΔU is the axial splitting parameter. The zero-field splitting parameter (Dquin) within an effective quintet state, generated from the three local effective spins (1/2), can be expressed as Dquin = Deff/3 + D’eff/6 [16].
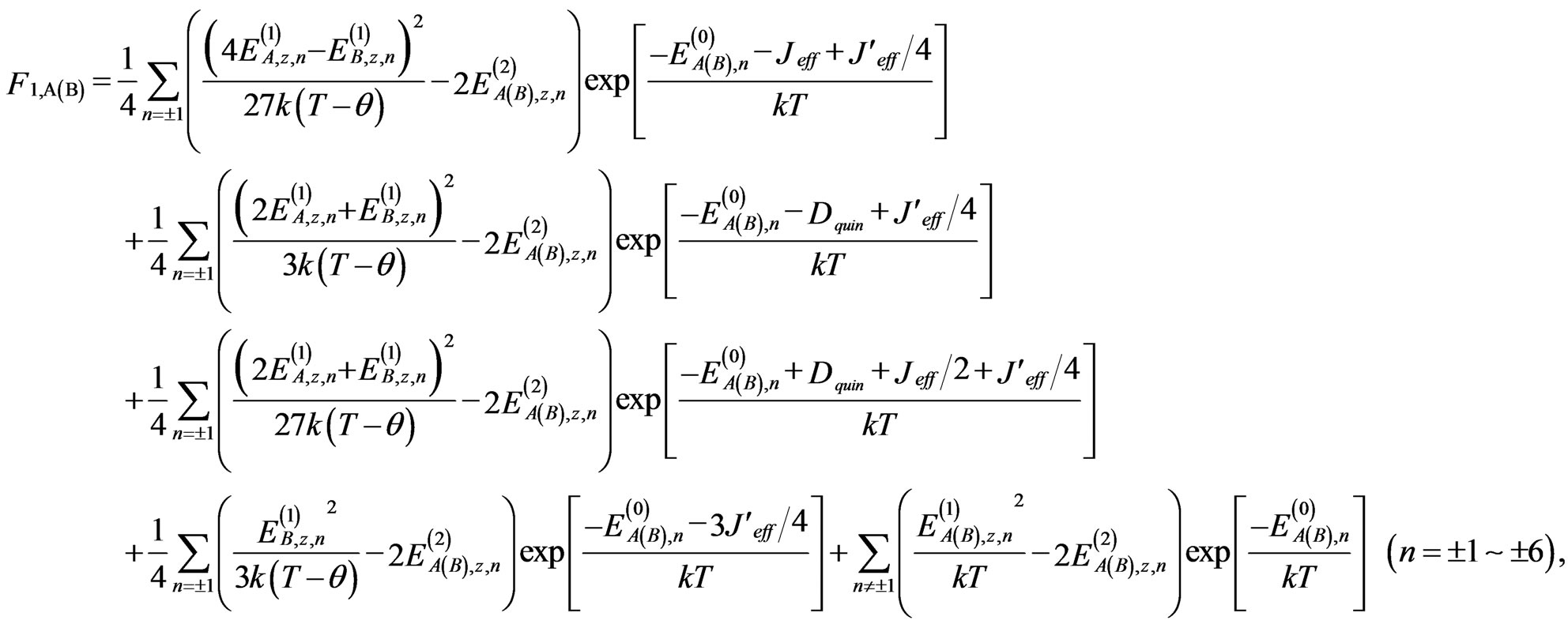
At this stage, the susceptibility equation can be expressed as follows:
 , (7)
, (7)
where θ is the Weiss constant to describe the intermolecular exchange interactions. This interaction is actually temperature-dependent, but it is approximated as a constant in this study. The zero-field energies and firstand second-order Zeeman coefficients for each cobalt(II) ion ,
, ,
, ,
,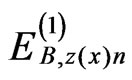 ,
,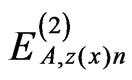 , and
, and  (n = ±1 - ±6) can be expressed using equations reported previously [5,6].
(n = ±1 - ±6) can be expressed using equations reported previously [5,6].
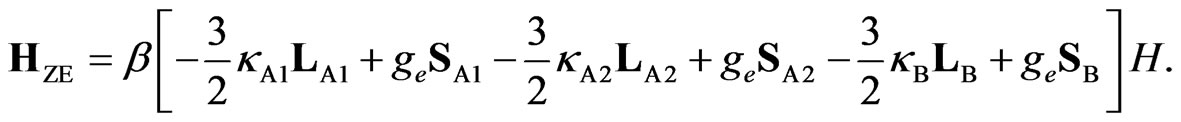 (3)
(3)
 (8)
(8)
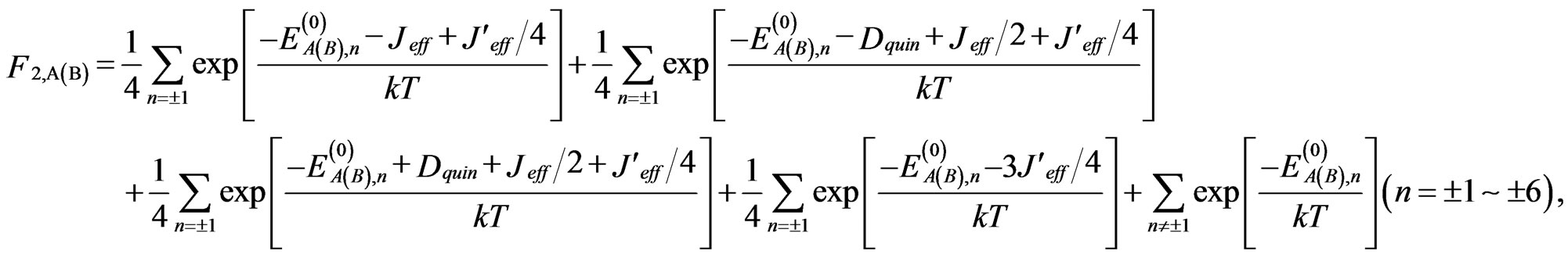 (9)
(9)
 (10)
(10)
3.2. Structural Features of 1 and 2
The crystal structures of 1 and 2 have been reported previously [15]; thus, only the structural features are briefly mentioned here. Both 1 and 2 have tricobalt(II) structures as shown in Figure 3, and the structures are very similar. Both ligands L1– and L2– have an N2O coordination site and an NO site (see Figure 1). The N2O site of a ligand incorporates a cobalt(II) ion (CoA), and another cobalt(II) ion (CoB) is incorporated by two NO sites of the two ligands, forming a trinuclear structure in the shape of an isosceles triangle. CoA and CoB are bridged by a phenolic oxygen atom of the ligand and an oxygen atom from an external acetate ion. Two CoA ions (CoA1 and CoA2) are bridged by two pairs of syn-anti bidentate oxygen atoms of two acetate ions. The coordination geometry for each cobalt(II) ion is distorted octahedral.
3.3. Magnetic Data Analysis
Magnetic data for complexes 1 and 2, as well as the preparations and crystal structures, were reported earlier [15], but no theoretical analysis of the data was made. The temperature dependencies of χM and µeff for the Co3 unit for 1 and 2 are shown in Figures 4 and 5, respectively. The µeff values for the Co3 unit for 1 and 2 at room temperature are 8.36 and 8.45 µB, respectively. These values are larger than the spin-only value of the high-spin cobalt(II) ion (6.71 µB; µSO = [3{4S(S+1)}]1/2; S = 3/2) but close to the value expected when the spin momentum and orbital momentum exist independently [9.00 µB; µLS = [3{L(L+1)+ 4S(S+1)}]1/2; L = 3, S = 3/2]. This indicates a contribution of the orbital angular momentum typical of the local 4T1 ground term. Moreover, the characteristic slopes of µeff curves are typical for the result of spin-orbit coupling. Therefore, the data were analyzed using the equation in Section 3.1, considering the local axial distortions, the local spin-orbit couplings, the anisotropic exchange interactions, and the intermolecular exchange interactions. The obtained parameters are summarized in Table 1.
The orbital reduction factor κ corresponds to the delocalization of unpaired electrons from metal ions to ligand, but it also contains the admixture of the upper 4T1(4P) state into the 4T1(4F) ground state. The κ value is known to be ~0.93 for the free cobalt(II) ion [4,17], and the obtained κA and κB values for both complexes are close to the free ion value. Comparing the axial splitting parameters ΔA and ΔB, ΔB is larger than ΔA for both complexes. All the Δ values for both complexes are normal for octahedral high-spin cobalt(II) complexes (~ 200 - ~ 800 cm–1) [3]. The spin-orbit coupling parameter λ for the free cobalt(II) ion is theoretically expected to be ~ –172 cm–1 [18], but is generally smaller in the complexes. For complex 1, the λA value is normal (~70% of the free ion value), whereas the λB value is slightly smaller than the normal value. This occurs presumably because the assumed symmetry is less suitable for CoB. That is, the local distortion axes are assumed to be parallel in this studyand this assumption may not be adequate. A similar tendency is also seen for complex 2.
The magnetic susceptibility below 50 K cannot be fitted without consideration of the exchange interactions. If we assume that there is no exchange interaction (J = 0.00 cm–1, J’ = 0.00 cm–1, and θ = 0.00 K), the calculated susceptibility curves are lower than the observed susceptibility below ~50K for both complexes as shown in

Figure 3. Schematic drawing of the tricobalt(II) structure for 1 (R = C2H5) and 2 (R = n-C3H7).

Figure 4. Temperature dependencies of χM (O) and µeff (∆) of complex 1. Solid curves are drawn with the parameters κA = 0.93, λA = –151 cm–1, ΔA = 604 cm–1, κB = 0.93, λB = –101 cm–1, ΔB = 714 cm–1, J = +0.01 cm–1, J’ = +1.51 cm–1, and θ = –0.61 K. The dashed curve in the insert is drawn with the parameters κA = 0.93, λA = –151 cm–1, ΔA = 604 cm–1, κB = 0.93, λB = –101 cm–1, ΔB = 714 cm–1, J = 0.00 cm–1, J’ = 0.00 cm–1, and θ = 0.00 K.

Figure 5. Temperature dependencies of χM (O) and µeff (∆) of complex 2. Solid curves are drawn with the parameters κA = 0.93, λA = –136 cm–1, ΔA = 531 cm–1, κB = 0.93, λB = –115 cm–1, ΔB = 674 cm–1, J = +0.01 cm–1, J’ = +1.76 cm–1, and θ = –1.08 K. The dashed curve in the insert is drawn with the parameters κA = 0.93, λA = –136 cm–1, ΔA = 531 cm–1, κB = 0.93, λB = –115 cm–1, ΔB = 674 cm–1, J = 0.00 cm–1, J’ = 0.00 cm–1, and θ = 0.00 K.
Figures 4 and 5. This indicates the existence of ferromagnetic interaction in both complexes. Considering both the intramolecular and intermolecular interactions, the data were successfully analyzed. The result indicated that the exchange interaction between CoA (CoA1 and CoA2) and CoB is practically negligible (J = ~ 0), but the interaction between CoA1 and CoA2 is ferromagnetic (J’ > 0). As mentioned above, CoA and CoB are bridged by a phenolic oxygen atom and an oxygen atom of an acetate

Table 1. Magnetic parameters and discrepancy factors for complexes 1 and 2.
ion, whereas CoA1 and CoA2 are bridged by two pairs of syn-anti bidentate oxygen atoms of two acetate ions. Since an exchange interaction parameter is described as the sum of the ferromagnetic and antiferromagnetoic components and a phenolate bridge generally contributes to an antiferromagnetic interaction, the result (J’ > J) is consistent with this idea.
Judging from the obtained parameters, we can explain the temperature dependencies as follows. The magnetic moments decrease with decreasing the temperature, and the decrease above 50 K is mainly due to the thermal population on the Kramers doublets generated from the local 4T1 ground term by the spin-orbit coupling. Below 50 K, the ferromagnetic interaction between CoA1 and CoA2 appears, and the drop below 10 K is due to the intermolecular antiferromagnetic interaction.
4. CONCLUSIONS
In this study, a new magnetic susceptibility equation was developed for trinuclear octahedral high-spin cobalt(II) complexes in the shape of an isosceles triangle considering the local axial distortion, the spin-orbit coupling, the exchange interactions, and the intermolecular exchange interactions. Using the equation, the magnetic data for two tricobalt(II) complexes 1 and 2 were successfully analyzed. For both complexes, ferromagnetic interaction between CoA1 and CoA2 ions and practically negligible interaction between CoA and CoB ions were observed.
5. ACKNOWLEDGMENTS
This work was supported by the Saneyoshi Scholarship Foundation.
REFERENCES
- Kahn, O. (1993) Molecular magnetism. VCH Publishers, New York.
- Lines, M.E. (1963) Magnetic properties of CoCl2 and NiCl2. Physical Review, 131, 546-555. doi:10.1103/PhysRev.131.546
- Figgis, B.N., Gerloch, M., Lewis, J., Mabbs, F.E. and Webb, G.A. (1968) The magnetic behaviour of cubic-field 4T1g terms in lower symmetry. Journal of Chemical Society A, 1, 2086-2093. doi:10.1039/j19680002086
- Lines, M.E. (1971) Orbital angular momentum in the theory of paramagnetic clusters. Journal of Chemical Physics, 55, 2977-2984. doi:10.1063/1.1676524
- Sakiyama, H., Ito, R., Kumagai, H., Inoue, K., Sakamoto, M., Nishida, Y. and Yamasaki, M. (2001) Dinuclear cobalt(II) complexes of an acyclic phenol-based dinucleating ligand with four methoxyethyl chelating arms— First magnetic analyses in an axially distorted octahedral field. European Journal of Inorganic Chemistry, 2001, 2027-2032.
- Sakiyama, H. (2001) Development of magsaki(A) software for the magnetic analysis of dinuclear high-spin cobalt(II) complexes considering anisotropy in exchange interaction. Journal of Chemical Software, 7, 171-178. doi:10.2477/jchemsoft.7.171
- Hossain, M.J., Yamasaki, M., Mikuriya, M., Kuribayashi, A. and Sakiyama, H. (2002) Synthesis, structure, and magnetic properties of dinuclear cobalt(II) complexes with a new phenol-based dinucleating ligand with four hydroxyethyl chelating arms. Inorganic Chemistry, 41, 4058-4062. doi:10.1021/ic0255297
- Sakiyama, H. (2006) Magnetic susceptibility equation for dinuclear high-spin cobalt(II) complexes considering the exchange interaction between two axially distorted octahedral cobalt(II) ions. Inorganica Chimica Acta, 359, 2097-2100. doi:10.1016/j.ica.2005.12.052
- Sakiyama, H. (2007) Magnetic susceptibility equation for dinuclear high-spin cobalt(II) complexes considering the exchange interaction between two axially distorted octahedral cobalt(II) ions. Inorganica Chimica Acta, 360, 715-716. doi:10.1016/j.ica.2006.06.011
- Tone, K., Sakiyama, H., Mikuriya, M., Yamasaki, M. and Nishida, Y. (2007) Magnetic behavior of dinuclear cobalt(II) complexes assumed to be caused by a paramagnetic impurity can be explained by tilts of local distortion axes. Inorganic Chemistry Communications, 10, 944-947. doi:10.1016/j.inoche.2007.04.028
- Palii, A.V., Tsukerblat, B.S., Coronado, E., ClementeJuan, J.M. and Borras-Almenar, J.J. (2003) Microscopic approach to the pseudo-spin-1/2 Hamiltonian for Kramers doublets in exchange coupled Co(II) pairs. Inorganic Chemistry, 42, 2455-2458.doi:10.1021/ic0259686
- Palii, A.V., Tsukerblat, B.S., Coronado, E., ClementeJuan, J.M. and BorrasAlmenar, J.J. (2003) Orbitally dependent magnetic coupling between cobalt(II) ions: The problem of the magnetic anisotropy. The Journal of Chemical Physics, 118, 5566-5581. doi:10.1063/1.1555122
- Palii, A.V., Tsukerblat, B.S., Coronado, E., ClementeJuan, J.M. and Borras-Almenar, J.J. (2003) Orbitally dependent kinetic exchange in cobalt(II) pairs: Origin of the magnetic anisotropy. Polyhedron, 22, 2537-2544. doi:10.1016/S0277-5387(03)00207-9
- Lloret, F., Julve, M. Cano, J., Ruiz-García, R. and Pardo, E. (2008) Magnetic properties of six-coordinated highspin cobalt(II) complexes: Theoretical background and its application. Inorganica Chimica Acta, 361, 3432-3445. doi:10.1016/j.ica.2008.03.114
- Adams, H., Fenton, D.E., Cummings, L.R., McHugh, P.E., Ohba, M., Okawa, H., Sakiyama, H. and Shiga, T. (2004) The structures and magnetism of trinuclear Ni(II), Co(II) and Mn(II) complexes derived from unsymmetrical compartmental ligands. Inorganica Chimica Acta, 357, 3648- 3656. doi:10.1016/j.ica.2004.03.055
- Scaringe, R.P., Hodgson, D.J. and Hatfield, W.E. (1978) The coupled representation matrix of the pair hamiltonian. Molecular Physics, 35, 701-713. doi:10.1080/00268977800100521
- Low, W. (1958) Paramagnetic and optical spectra of divalent cobalt in cubic crystalline fields. Physical Review, 109, 256-265. doi:10.1103/PhysRev.109.256
- Figgis B.N. and Hitchman, M.A. (2000) Ligand field theory and its application. Wiley-VCH, New York.

