Journal of Quantum Information Science
Vol.07 No.02(2017), Article ID:75758,5 pages
10.4236/jqis.2017.72004
Looped Light on Dark Energy*
Mohamed S. El Naschie
Department of Physics, Faculty of Science, University of Alexandria, Alexandria, Egypt

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 7, 2017; Accepted: April 25, 2017; Published: April 28, 2017
ABSTRACT
We give a mathematical golden mean distribution based probabilistic confirmation of a recent spectacular experiment with light. The experiment in question is a three-slit variant of the well known two-slit set up of quantum mechanics. The outcome of the sophisticated experiment revealed the looped path of light on the quantum scale and consequently the Peano-Hilbert geometry of spacetime, ergo its fractal-Cantorian nature. The mathematics used here on the other hand is the remarkably simple and insightful golden mean probability distribution known from a famous paradox known in social sciences as the voter paradox.
Keywords:
Dark Energy, the Voter Paradox, Golden Mean Distribution, Looped Light, the Triple-Slit Experiment, Cantorian-Fractal Spacetime

1. Introduction
In [1] , Nobel Laureate Gerardus ‘tHooft wrote:
“… The physics of elementary particles has nothing to do with the physics of low temperature, but the mathematics is very, very similar… What a nice feature of theoretical physics! Totally different worlds can be compared with each other, just because they happen to obey similar mathematical equations.”
In the present letter we take ‘tHooft’s words much further than we could have thought possible by comparing the voter paradox of political sciences [2] with the outcome of the triple-slit experiment [3] [4] [5] simply because both theories not only obey identical mathematics but also stand in an almost one to one analogical correspondence to each other [2] . Needless to say, this correspondence is far from being accidental and is basically deeply rooted in number theory and the golden ratio with its now well documented relation to physics and life [5] - [13] .
2. Background Information of a Paradox from Mathematical Socio-Political Science
The voter paradox with its golden mean distribution [7] [8] is a highly non-tri- vial and interesting subject in the mathematical theory of probability and has well known profound implications in social and political sciences [1] [11] . In particular and similar to Hardy’s quantum entanglement [9] [10] , the golden mean appears as the solution which can be stated in an unexpected but rather simple theorem [1] [6] [7] [11] . It is the aim of the present letter to show how this said theorem can be applied to the triple-slit experiment in a way quite similar to earlier solutions of the two-slit experiment [14] [15] .
We start with the probabilistic mathematics of the voter paradox [1] [11] . This could be stated as follows [1] :
Let X, Y and Z be random variables and the corresponding probabilities are denoted by P(X), P(Y) and P(Z).
Theorem:
For independent X, Y and Z all the three probabilities P(X), P(Y) and P(Z) can be as large as the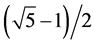 , i.e. the golden mean and its value is the largest possible.
, i.e. the golden mean and its value is the largest possible.
For details the reader is referred to the relevant literature [1] [11] .
3. Analogy and Correspondence
In this part we give a short account of the analogical correspondence between the voter paradox and the looped light experiment [3] [5] which we alluded to earlier on. Now in the triple-slit experiment we have three “holes” where the random “photons” pass through and the obvious crucial point is that we may identify the probability of photons going through them with the three probabilities [1] [11]
 (1)
(1)
where 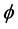 is the golden mean given in the preceding theorem. Consequently for the experimental physical set up to obey the simultaneity forbidden by classical mechanics but admitted by the way-particle duality of quantum mechanics we see that the probability corresponding to the looped light of the three-slit experiment must be [10] - [15]
is the golden mean given in the preceding theorem. Consequently for the experimental physical set up to obey the simultaneity forbidden by classical mechanics but admitted by the way-particle duality of quantum mechanics we see that the probability corresponding to the looped light of the three-slit experiment must be [10] - [15]
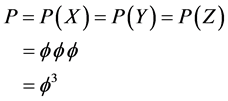 (2)
(2)
Note that Equation (2) corresponds to the counterfactual part of Hardy’s quantum entanglement 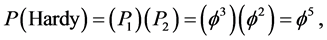 i.e.
i.e. 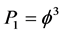 and reflects also the very structure of empty spacetime [9] [10] [12] [13] [14] [15]
and reflects also the very structure of empty spacetime [9] [10] [12] [13] [14] [15]
where 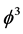 is nothing but the inverse of the Hausdorff dimension of the fractal Cantorian core of spacetime, namely
is nothing but the inverse of the Hausdorff dimension of the fractal Cantorian core of spacetime, namely 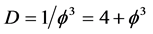 according to the von Neumann-Connes dimensional function [9] [14] [15] .
according to the von Neumann-Connes dimensional function [9] [14] [15] .
4. Discussion
From the preceding simple chain of thought it is obvious that we may interpret the results of Equation (2) as a confirmation of the fractal-Cantorian nature of spacetime [14] [15] and therefore also a confirmation of the Peano-Hilbert dynamics resembling the looped light result of the recent remarkable experiment of Refs. [3] [4] [5] . It is interesting to see the utter simplicity of our interpretation. For instance one slit only would correspond to 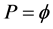 which is a quantum particle in the E-infinity interpretation, i.e. the zero set [4] [5] [16] . If we open two slits we obtain
which is a quantum particle in the E-infinity interpretation, i.e. the zero set [4] [5] [16] . If we open two slits we obtain 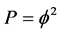 which is the quantum wave, i.e. the empty set [16] . Finally
which is the quantum wave, i.e. the empty set [16] . Finally  is what will give us the cobordism of the wave which is empty spacetime [16] . This is a key point in understanding quantum mechanics in a way which we feel could appeal to the view point of many deep thinkers such as ‘tHooft [1] . It is really a deceptively harmless point but on a deep level mean nothing less than replacing the mysterious wave collapse, i.e. state vector reduction by an obvious move from a zero set to an empty set [16] .
is what will give us the cobordism of the wave which is empty spacetime [16] . This is a key point in understanding quantum mechanics in a way which we feel could appeal to the view point of many deep thinkers such as ‘tHooft [1] . It is really a deceptively harmless point but on a deep level mean nothing less than replacing the mysterious wave collapse, i.e. state vector reduction by an obvious move from a zero set to an empty set [16] .
Interestingly we could take a special case of the voter paradox namely the Steinhaus-Trybula paradox [11] where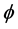 is replaced by
is replaced by 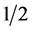 and find using the preceding mathematics the following dimensions for an idealized spacetime namely [9] [10] [12] [13] [16]
and find using the preceding mathematics the following dimensions for an idealized spacetime namely [9] [10] [12] [13] [16]
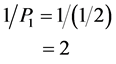 (3)
(3)
which is the two Brane of a string world sheet [9] [10] [12] [13] while
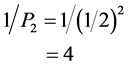 (4)
(4)
is our classical spacetime and finally
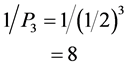 (5)
(5)
which is super space of super symmetry [16] [17] . It really is as simple as that once our set theoretical considerations are taken seriously [14] [15] [16] [17] .
5. Conclusion
The golden mean probability resolution of the voter paradox is applied in the present work to the triple-slit experiment of looped light. In a nutshell our analysis lends a firm probabilistic underpinning of a highly non-classical quantum phenomenon without direct reference to quantum mechanics. In general we hope that we showed with utter simplicity that measurement naturally converts an empty set to a zero set which means a quantum wave to a quantum particle. In other words, it is all nothing more than the topological density of spacetime. That is exactly why we think the looped light is an experimental proof for the fractal nature of quantum spacetime and that dark energy and dark matter are real consequences of the topology and geometry of quantum spacetime.
Acknowledgements
The first time I learned of the voter paradox was from my then Ph.D. supervisor, Prof. J. M. T. Thompson, FRS around 1970. Amazingly the subject remained dormant in my subconscious for almost 47 years. I am grateful in all events to Prof. Thompson for expanding my horizons beyond civil engineering.
Cite this paper
El Naschie, M.S. (2017) Looped Light on Dark Energy. Journal of Quantum Information Science, 7, 43- 47. https://doi.org/10.4236/jqis.2017.72004
References
- 1. ‘tHooft, G. (1997) In Search of the Ultimate Building Blocks. Cambridge University Press, Cambridge, 68-69.
- 2. Pittman, J. (1993) Probability. Springer, New York, USA, 254.
- 3. Magana-Loaiza, O.S., de Leon, I., Mirhosseini, M., et al. (2016) Exotic Looped Trajectories in the Three-Slit Interference. ArXiv:1610.0858V1[quant-ph]
- 4. El Naschie, M.S. (2017) The Quantum Triple-Slit Experiment and Cosmic Dark Energy. Open Journal of Microphysics, 7, 31-35.
https://doi.org/10.4236/ojm.2017.72002 - 5. El Naschie, M.S. The Looped Light of the Triple-Slit Real Experiment as a Confirmation for the Extra Dimensions of Quantum Spacetime and the Reality of Dark Energy. Optical and Photonic Journal, in Press.
- 6. Ping, S. (2012) Golden Ratio Estimate of Success Probability Based on One and Only. ArXiv:1207.5198
- 7. Tanackov, I., Tepic, J. and Kostelac, M. (2011) The Golden Ratio in Probabilistic and Artificial Intelligence. Tehnickivjesnik/Technical Gazette, 18, 641-647.
- 8. Hayata, K. (2014) Golden Distribution of Probabilities. Forma (Letter), 29, 33-40.
https://doi.org/10.5047/forma.2014.006 - 9. He, J.-H., Marek-Crnjac, L., et al. (2011) Quantum Golden Mean Entanglement Test as the Signature of the Fractality of Micro Spacetime. Nonlinear Science Letters B, 1, 45-50.
- 10. Marek-Crnjac, L. (2006) The Golden Mean in the Topology of Four Manifolds in Conformal Field Theory, in Mathematical Probability Theory and in Cantorian Spacetime. Chaos, Solitons & Fractals, 28, 1113-1118.
https://doi.org/10.1016/j.chaos.2005.08.160 - 11. Jackson, M. (2004) Paradoxes with Dice and Election. In: Tadich, B., Tabias, S., et al., Eds., Towards Excellence in Mathematics; Proceedings of the 4th Annual Conference of the Mathematical Association of Victoria, Monash University, Clayton, Australia, 2004, 208-218.
- 12. El Naschie, M.S. (2007) Hilbert Space, Poincaré Dodecahedron and Golden Mean Transfiniteness. Chaos, Solitons & Fractals, 31, 787-793.
https://doi.org/10.1016/j.chaos.2006.06.003 - 13. El Naschie, M.S. (1998) On the Uncertainty of Cantorian Geometry and the Two-Slit Experiment. Chaos, Solitons & Fractals, 19, 517-529.
https://doi.org/10.1016/S0960-0779(97)00150-1 - 14. El Naschie, M.S. (2004) A Review of E-Infinity Theory and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19. 209-236.
https://doi.org/10.1016/S0960-0779(03)00278-9 - 15. El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646.
https://doi.org/10.1016/j.chaos.2008.09.059 - 16. El Naschie, M.S. (2015) An Exact Mathematical Picture of Quantum Spacetime. Advances in Pure Mathematics, 5, 560-570.
https://doi.org/10.4236/apm.2015.59052 - 17. El Naschie, M.S. (2016) On a Fractal Version of Witten’s M-Theory. Journal of Astronomy & Astrophysics, 6, 135-144.
NOTES

*This paper is dedicated to Nobel Laureate Gerardus ‘tHooft, one of a handful of the architects of modern physics who think that quantum mechanics is on a very deep level basically deterministic which was, and still is the Author’s firm belief even when the mathematical tools to show this may be remarkably different.

