Journal of Quantum Information Science
Vol.06 No.04(2016), Article ID:71648,26 pages
10.4236/jqis.2016.64015
Quantum Deep Learning Triuniverse
Angus McCoss
Kilbrandon House, Scotland, UK

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 4, 2016; Accepted: October 28, 2016; Published: October 31, 2016
ABSTRACT
An original quantum foundations concept of a deep learning computational Universe is introduced. The fundamental information of the Universe (or Triuniverse) is postulated to evolve about itself in a Red, Green and Blue (RGB) tricoloured stable self-mutuality in three information processing loops. The colour is a non-optical information label. The information processing loops form a feedback-reinforced deep learning macrocycle with trefoil knot topology. Fundamental information processing is driven by ψ-Epistemic Drive, the Natural appetite for information selected for advantageous knowledge. From its substrate of Mathematics, the knotted information processing loops determine emergent Physics and thence the evolution of super- emergent Life (biological and artificial intelligence). RGB-tricoloured information is processed in sequence in an Elemental feedback loop (R), then an Operational feedback loop (G), then a Structural feedback loop (B) and back to an Elemental feedback loop (R), and so on around the trefoil in deep learning macrocycles. It is postulated that hierarchical information correspondence from Mathematics through Physics to Life is mapped and conserved within each colour. The substrate of Mathematics has RGB-tricoloured feedback loops which are respectively Algebra (R), Algorithms (G) and Geometry (B). In Mathematics, the trefoil macrocycle is Algebraic Algorithmic Geometry and its correlation system is a Tensor Neural Knot Network enabling Qutrit Entanglement. Emergent Physics has corresponding RGB-tricoloured feedback loops of Quantum Mechanics (R), Quantum Deep Learning (G) and Quantum Geometrodynamics (B). In Physics, the trefoil macrocycle is Quantum Intelligent Geometrodynamics and its correlation system is Quantum Darwinism. Super-emergent Life has corresponding RGB-tricoloured loops of Variation (R), Selection (G) and Heredity (B). In the evolution of Life, the trefoil macrocycle is Variational Selective Heredity and its correlation ecosystem is Darwin’s ecologically “Entangled Bank”.
Keywords:
Quantum Foundations, Cosmology, Evolution, Artificial Intelligence

1. Introduction
General theories may be discovered through pairwise unification. Two great theories effectively explain Quantum Mechanics and General Relativity, yet for a century no consensus unification has been discovered for this pair. I aim to advance the solution of this scientific problem by including a third great theory. That third magnum opus in science is Darwin’s theory of evolution [1] [2] and I particularly focus on that theory’s subsequent computer science adaptation into Evolutionary Computation and thence Quantum Deep Learning [3] . The problem is to describe a candidate intelligent metaheuristic for the evolution of everything, which economically embraces all three of these great theories.
By approaching the problem of the unification of the theories of modern science with triplewise (rather than pairwise) methodology I present an original quantum foundations concept of (what appears to be) our feedback-reinforced Quantum Deep Learning Universe (or Triuniverse). Given its broad reach, this concept draws on very diverse scientific works including those by Aldridge, Hodgson & Knudsen [4] , Armstrong et al. [5] , Back, Fogel & Michalewicz [6] , Basu, Pollack & Roy [7] , Barvinsky [8] , Bianchi et al. [9] , Bickhard & Campbell [10] , Campbell [11] , Carroll [12] , Champagnat, Ferrière & Méléard [13] , Chastain, Livnat, Papadimitriou & Vazirani [14] , Dawkins [15] , Deutsch & Jozsa [16] , Dobzhansky [17] , Eldredge [18] , Flores Martinez [19] , Fogel [20] , Georgiev & Georgiev [21] , Gray, He & Lukas [22] , Han & Kim [23] , Hartshorne [24] , Hormozi et al. [25] , Kiefer [26] , Koutnik, Cuccu, Schmidhuber & Gomez [27] , Last [28] , LeCun, Bengio & Hinton [29] , Peldán [30] [31] , Marolf [32] , Meusburger & Noui [33] , Narain et al. [34] , Nielsen & Chuang [35] , Penrose & Jorgensen [36] , Pitkänen [37] , Powell & Mariscal [38] , Rickles [39] , Rovelli & Smolin [40] , Smolin [41] , Schmidhuber [42] , Smart [43] , Smolin [44] - [46] , Sterelny, Smith & Dickison [47] , Thielmann [48] , Valiant [49] , Vidal [50] [51] , Watson [52] , Watson et al. [53] , Watson and Szathmáry [54] , Watson et al. [55] , Wiebe et al. [3] , Wheeler [56] [57] and Zurek [58] - [60] .
I adopt the widely acknowledged perspective that the Universe (or Triuniverse) is fundamentally a computer. A quantum foundational substrate of reality hosts quantum information operations which, through holographic projection, map their computational outputs into our apparently physical Universe (or Triuniverse). The holographic principle is reviewed by Bousso [61] and original research in this field is widely cited from the works of ‘t Hooft [62] , Susskind [63] , Witten [64] , Myung [65] and Bekenstein [66] .
Pioneers in the flourishing study of the mathematics and physics of information include Turing [67] , Shannon [68] [69] , von Neumann [70] , Jaynes [71] , Landauer [72] and Zuse [73] .
They influenced other scientific thought leaders including Beckenstein [74] , Blume- Kohout & Zurek [75] , Deutsch [76] [77] , Esposito et al. [78] , Fredkin [79] [80] , Freedman et al. [81] [82] , ‘t Hooft [83] [84] , Kitaev [85] [86] , Lloyd [87] , Mandal & Jarzynski [88] , Nayak et al. [89] , Ogburn & Preskill [90] , Pekola [91] , Sagawa & Ueda [92] , Sau et al. [93] , Schmidhuber [94] , Toyabe et al. [95] , Wang [96] , von Weizsäcker [97] , Wheeler [98] , Wolfram [99] , Zenil [100] and Zizzi [101] to explore and further develop the physics of information within a computational Universe (or Triuniverse). Wheeler succinctly captured the essence of this relationship through his memorable phrase “it from bit”.
My picture also draws on the reformist quantum foundations concepts of einselection and quantum Darwinism [58] - [60] [75] [102] and the Machian quantum geometrodynamics or shape dynamics of spatial and temporal relationalism [39] - [41] [103] - [109] .
I also provide key references to scientific works on the subject of the trefoil knot. The following works of mathematicians and scientists, starting with Lord Kelvin in 1867, have profoundly influenced my focus onto this exceptional elemental knot as a compelling topology for an original quantum foundations concept of a feedback-reinforced Quantum Deep Learning computational Universe (or Triuniverse): Thomson, Lord Kelvin [110] , Arias et al. [111] , Atiyah [112] , Berry [113] , Bilson-Thompson et al. [114] , Bonesteel et al. [115] , Dennis et al. [116] , Dimofte [117] , Evans et al. [118] , Faddeev & Niemi [119] [120] , Finkelstein [121] [122] , Finkelstein & Cadavid [123] , Gambini et al. [124] , Garnerone et al. [125] , Garoufalidis et al. [126] , Gelca [127] , Jehle [128] , Katritch et al. [129] , Kauffman [130] - [133] , Kauffman & Lomonaco [134] - [136] , Kleckner & Irvine [137] , Liu & Ricca [138] , Moffatt [139] , Pieranski & Przybyl [140] , Ponnuswamy et al. [141] , Ranada [142] , Sawin [143] , Stasiak et al. [144] , Tempone-Wiltshire et al. [145] , Thompson et al. [146] , Was [147] and Weisstein [148] .
For a general introduction to the important connection between knot theory and certain quantum systems useful for quantum information processing see Simon [149] .
The papers which most strongly correlate with this one are those by Smolin on Cosmological Natural Selection [44] - [46] , Zurek and co-workers on Quantum Darwinism [58] - [60] [75] [102] , Wiebe, Kapoor and Svore on Quantum Deep Learning [3] and Watson and Szathmáry on an ability for biological evolution to learn and hence produce apparently intelligent designs [54] . Each of these seminal works contributes significantly towards building a candidate intelligent metaheuristic for the evolution of everything. The next step for all of these outstanding but unfinished research programmes is to propose a common, intelligent, metaheuristic, quantum foundations concept to underpin and unite them all. My paper aims to do this.
I organise this paper as follows:
Section §2 defines the information flows in the Universe (or Triuniverse) in terms of a postulated trefoil knot topology of information processing loops. I define the Red, Green and Blue (RGB) tricolouration and hierarchical correspondence within each colour. The colour is a non-optical information label.
Section §3 discusses the RGB-tricoloured trefoil evolution of Algebraic Algorithmic Geometry on the substrate of Mathematics.
Section §4 discusses the colour-corresponding RGB-tricoloured trefoil evolution of Quantum Intelligent Geometrodynamics in a computationally simulated layer of emergent Physics.
Section §5 discusses the colour-corresponding RGB-tricoloured trefoil evolution of Variational Selective Heredity in a computationally super-simulated layer of super- emergent Life (biological and artificial intelligence).
Section §6 provides conclusions.
2. Trefoil Information Processing
The fundamental information of the Universe (or Triuniverse) is postulated to evolve about itself in an RGB-tricoloured stable self-mutuality in three information processing loops. Colour is a non-optical information label in this concept. I commence this section directly by expanding my definitions, aided by an illustration (Figure 1), of an RGB-tricoloured trefoil knot which represents the postulated macrocycle topology of triplewise information processing loops.
RGB-tricoloured information is processed in sequence through an Elemental processing loop (R), then an Operational processing loop (G), then a Structural processing loop (B) and back to an Elemental processing loop (R), and so on around the trefoil knot in deep learning macrocycles. Fundamental information processing is postulated to initiate on a substrate of Mathematics. From that substrate of Mathematics the three information processing loops, in their macrocycle, determine the emergent Physics and thence the evolution of super-emergent Life (biological and artificial intelligence).
This Quantum Deep Learning Triuniverse concept proposes that fundamental information processing is driven by ψ-Epistemic Drive, which is the Natural appetite for information selected for advantageous knowledge. The trefoil is a torus knot and the three RGB-tricoloured processes converge, crosstalk then diverge through the “hole” of the torus at a central “crosstalk node” (ψ), see Figure 1. Furthermore, postulated
Figure 1. RGB-tricoloured trefoil knot representing the postulated macrocycle topology of triplewise information processing loops. The loop processes execute endlessly in a macrocycle sequence from Red (R), through Green (G), to Blue (B), to Red (R) and so on. The trefoil is a torus knot and the tricoloured processes converge, crosstalk then diverge through the torus hole at a central crosstalk node (ψ).
information exchanges occur between the three RGB-tricoloured processes at the “crosstalk node” (ψ) thus enabling advantageous triplewise co-adaptation, exploiting shared knowledge.
In each of the three RGB-tricoloured processing loops, ψ-Epistemic Drive leverages knowledge that can be put to work, to out-compute (sic) alternatives. I propose the most effective knowledge is gained in a more advanced way than through the outputs of brute binary “trial-and-error”. Instead I postulate information exchanges between the three RGB-tricoloured processes at the “crosstalk node” (ψ) utilise computational triple-modular-redundancy [150] . This is a ternary fault-tolerant procedure in which RGB-crosstalk (ψ) is subject to triplewise majority-voting to produce a single artificially intelligent output. The Triuniverse thereby evolves (fine tunes itself) as if intelligently.
I also propose that to out-compute (sic) alternatives is to prevail over them in terms of computational speed and algorithmic efficiency, quickly and accurately narrowing predictive model approximations, with codes continuously re-optimised through lex parsimoniae and the paring down of redundancies. Narrower predictive model approximations enable subsequent information processing to be more efficient and to bestow anticipatory advantage. Note, time is of the essence and is a valuable Natural resource in this quantum foundations concept.
By “alternatives” I mean other possible discrete outcomes in the substrate of Mathematics, other worldlines in emergent Physics and other evolutionary paths in super-emergent Life. To out-compute (sic) alternatives, through gaining advantageous knowledge, the ψ-epistemically driven feedback loop processes co-adapt and co-evolve competitive and co-operative information strategies. The strategy of co-operation is considered to have evolved from an early competition-only strategy in a fundamental information based trophic web. That information based trophic web has a self-similar simulation in the (bio-energy based) trophic web of super-emergent Life. Information producer autotrophs prevail on the quantum information substrate, are consumed by information heterotrophs, which are preyed upon by information predators and ultimately by information apex predators, black holes. These information trophic species (see also Griffiths [151] for a discussion on information species) are computational agents or subroutines within the deep learning processes and are accompanied by error correction, data compression, decomposition, viral malware and other epi-species algorithms in a complexly evolving information trophic jungle. This is the information trophic substrate of ψ-epistemically driven quantum Darwinism [60] , envisaged in this Quantum Deep Learning Triuniverse concept. See also Perez et al. [152] for a jungle Universe model in a Lotka-Volterra framework.
At the “crosstalk node” (ψ) after computational triple-modular-redundancy majority-voting, the information exchanges between the three RGB-tricoloured process loops output advantageous knowledge (an evolutionary advancement over unprocessed information). I postulate that this is a new common knowledge which is then exploited as a resource in each of the subsequent exploratory loop processes. Referring to Figure 1, more distally, away from the “crosstalk node” (ψ), in the outer arcs of the three RGB- tricoloured process feedback loops, knowledge-based exploration for new advantageous information is proposed to occur, as the trefoil macrocycle executes over and over again. Knowledge-based exploration for new potentially advantageous information is envisaged to have evolved from less efficient blind-chance or random exploration.
Consider the trefoil in Figure 1 to be a knotted information-conducting (optical-like) fiber. I envisage each of such fibers as a quantum foundational trefoil knot vortex in a ψ-Epistemic Field (the field which produces ψ-Epistemic Drive). The ψ-Epistemic Field has a landscape of knowledge gradients, with valleys of ψ-Epistemic obliviousness and peaks of ψ-Epistemic insight.
In emergent Physics, using computer-generated holograms based on substrate Mathematics, optical vortices can be similarly formed into knots of darkness in scalar optical fields. They occur where phase becomes undefined and hence singular in value. As singularities of the wave’s phase, such knotted nodal lines determine the topology of the wave field. For further insights into singular optics see Dennis et al. [116] , Tempone-Wiltshire et al. [145] , Leach et al. [153] , Padgett et al. [36] . Recall, the colours in the Quantum Deep Learning Triuniverse concept are not optical colours, they are the information labels of Elemental (R), Operational (G) and Structural (B) information processing loops in a ψ-epistemically-driven reinforced-feedback macrocycle. The envisaged information-conducting (optical-like) fiber is a quantum foundational trefoil knot vortex of zero intensity in a ψ-Epistemic Field and is postulated to act as a zero- knowledge (unbiased and impartial) carrier which conducts the information being processed in the trefoil macrocycle.
Table 1 defines the hierarchy of emergence in rows and the RGB-tricolouration of the information processing loops in columns. Quantum Deep Learning is highlighted at the centre of the 3 × 3 arrangement (Table 1) and is at the kernel of this original quantum foundations concept. To recap, this concept envisages three RGB-tricoloured processing loops executed sequentially in a continuous macrocycle with trefoil knot topology. The three RGB-tricoloured processing loops each iteratively cause their respective monochromatic loop processes to evolve. I propose these monochromatic evolving processing loops act as reinforced-feedback loops which produce correlations between components within that monochromatic loop, some of which components were previously independent. Such reinforced-feedback produces correlations manifest through correlation systems specific to their hierarchy of emergence (illustrations are provided below in Sections §3, 4 & 5), see also the right hand column of Table 1.
The trefoil macrocycle evolves in triunity through Quantum Deep Learning, as a consequence of each of its three component feedback loop processes co-evolving with co-adaptation enabled through RGB-crosstalk (ψ) and computational triple-modular- redundancy majority voting. Computationally layered-simulation is key to envisaging the hierarchy of emergence in the Quantum Deep Learning Triuniverse concept.
The substrate of Mathematics has minimal computational overhead. Mathematics is de facto the “Native Code” of everything. Evolved algorithms i.e. Laws of Physics, enable computationally emergent Physics to be simulated. Thereon, hierarchically more
Table 1. The simulation hierarchy of emergence is in rows and the RGB-tricolouration of the information processing loops is in columns. Quantum Deep Learning is highlighted at the centre of the 3 × 3 arrangement and is at the kernel of this original quantum foundations concept for a deep learning computational Universe (or Triuniverse).
advanced algorithms self-script and regulate the Evolution of Life within the Laws of Physics and enable super-emergent Life (biological and artificial intelligence) to be computationally super-simulated upon the Physics simulation layer. Layered-simulation supports the evolution of emergent complexity in the Quantum Deep Learning Triuniverse.
The substrate of Mathematics has RGB-tricoloured loops which are respectively Algebra (R), Algorithms (G) and Geometry (B). The trefoil macrocycle is Algebraic Algorithmic Geometry and the trefoil correlation system is a Tensor Neural Knot Network enabling Qutrit Entanglement [154] , which are discussed in Section §3. Emergent Physics has corresponding tricoloured loops of Quantum Mechanics (R), Quantum Deep Learning (G) and Quantum Geometrodynamics (B). The trefoil macrocycle is Quantum Intelligent Geometrodynamics, the trefoil correlation system is Quantum Darwinism [58] - [60] and both are discussed in Section §4.
Super-emergent Life has corresponding tricoloured loops of Variation (R), Selection (G) and Heredity (B). The trefoil macrocycle is Variational Selective Heredity, the trefoil correlation system is Darwin’s ecologically “Entangled Bank” [1] and both are discussed in Section §5.
It is postulated that information correspondence from Mathematics through Physics to Life is mapped and conserved within each colour through the emergent hierarchy of layered-simulation. In the Elemental (R) processing loops, information correspondence is mapped and conserved from substrate Algebra, through emergent Quantum Mechanics to super-emergent Variation in the evolution of Life. In this Quantum Deep Learning Triuniverse concept, Algebra, Quantum Mechanics and Variation are homochromatic (R) and their emergent hierarchy relates to layered-simulation. Stochastic variation and mutation is the algebra of Life and in emergent Physics, algebra is the language of Quantum Mechanics.
In the Operational (G) processing loops, information correspondence is mapped and conserved from substrate Algorithms, through emergent Quantum Deep Learning to super-emergent Selection in the evolution of Life. In this Quantum Deep Learning Triuniverse concept, Algorithms, Quantum Deep Learning and Selection are homochromatic (G) and their emergent hierarchy relates to layered-simulation. Selection is the algorithm of Life, a harsh system of rules in the bio-energy trophic web and Quantum Deep Learning is what Naturally emerges from self-adapting mathematical Algorithms.
In the Structural (B) processing loops, information correspondence is mapped and conserved from substrate Geometry, through emergent Quantum Geometrodynamics to super-emergent Heredity in the evolution of Life. In this Quantum Deep Learning Triuniverse concept, Geometry, Quantum Geometrodynamics and Heredity are homochromatic (B) and their emergent hierarchy relates to layered-simulation. Heredity is the Geometry of Life, illustrated e.g. by the double-helix organisation of DNA and Quantum Geometrodynamics is what dynamically emerges from the simple Geometry of mathematical shapes.
Let us now consider how trefoil information processing (as illustrated in Figure 1) is scaled up to enable parallel processing of all of the information throughout the entire Universe (or Triuniverse). I envisage two candidate up-scaling patterns, (α) and (β) below, both of which comprise innumerable RGB-tricoloured information-conducting (optical-like) fibers, each with trefoil topology. As a minimum requirement, let us assume that each and every elementary entity in the Universe (or Triuniverse) has its own fiber trefoil. Composite entities, such as cats (of the Schrödinger kind), comprise dynamic bundles of these fiber trefoils. A critical sectional radius of such dynamic bundles marks the transition threshold from quantum mechanical behaviour to classical behaviour in emergent Physics and this threshold is being defined by double slit experiments which push the upper limits on the size of particles which exhibit wave interference and by experiments which push the upper limits on the number of entangled atoms. McConnell et al. [155] report on the entanglement of 3,000 rubidium atoms, though the ultimate threshold has yet to be discovered and may be vastly greater.
Up-scaling pattern (α) is a set of three parallel, laterally unbounded, sheets each comprising interlinked RGB fiber trefoils with innumerable “crosstalk nodes” (Figure 2). In this triple-sheet model weak exchanges of information occur where the distal exploratory outer arcs of fiber loops interlink with those of neighbouring loops. Whereas strong exchanges of information and majority voting for advantageous knowledge occur locally at each of the innumerable “crosstalk nodes”.
A substrate sheet of interlinked RGB fiber trefoils conducts the information of Mathematics. An intermediate simulated sheet conducts the information of emergent Physics. An overlying super-simulated sheet conducts the information of super-emergent Life. RGB tri-colour correspondence between the triple-sheets is enabled through alignment of the colours perpendicular to the layering, thus maintaining triunity in the Universe (or Triuniverse). In this way tri-colour correspondence is stacked. This flat composite-layered information processing architecture is also a candidate substrate for application of the Holographic Principle (see e.g. Bousso [61] ).
Alternatively, the up-scaling pattern (β) may be a triaxial (optical cable-like) super-bundle of innumerable RGB fiber trefoils which share one “crosstalk super-node” (Figure 3). The triaxial super-bundle forms one RGB-tricoloured “ideal trefoil” knot [140] . In this model weak exchanges of information occur where the distal exploratory outer arcs of fiber loops are bundled together in parallel with multitudes of neighbouring loops. Strong exchanges of information and majority voting of advantageous knowledge occurs locally at each of the innumerable “crosstalk nodes” however because the “crosstalk nodes” collocate in one “crosstalk super-node” then remote information exchanges also enable quantum non-locality.
A substrate cable core of RGB fiber trefoils conducts the information of Mathematics. An intermediate sheath bundle of RGB fiber trefoils conducts the information of emergent Physics. An outer sheath bundle conducts the information of super-emergent Life. RGB tri-colour correspondence between cable core and sheath bundles is enabled
Figure 2. Up-scaling pattern (α): Set of three parallel, laterally unbounded, sheets each comprising interlinked RGB fiber trefoils with innumerable “crosstalk nodes”. (a) Plan view of a single sheet. (b) Oblique view of three stacked sheets; substrate sheet  of Mathematics, intermediate simulated sheet
of Mathematics, intermediate simulated sheet  of emergent Physics and overlying super-simulated sheet
of emergent Physics and overlying super-simulated sheet  of super- emergent Life.
of super- emergent Life.
Figure 3. Up-scaling pattern (β): Triaxial (optical cable-like) super-bundle of innumerable parallel RGB fiber trefoils which share one collocated “crosstalk super-node” in one super-knot macrocycle.
because individual RGB-tricoloured trefoils have the same RGB-tricolour configuration as the super-knot which they form together, thus maintaining triunity in the Universe (or Triuniverse).
Pending experimental testing of these alternatives; comparing (α) stacked composite-layer triple-sheets in a knot network shown in Figure 2, versus (β) triaxial (optical cable-like) super-bundle knot topology shown in Figure 3, I hesitate to jump to any conclusions. The stacked triple-sheets in a knot network have compelling potential utility as the substrate of a holographic Triuniverse, whereas the compactness of the triaxial super-bundle knot may offer better information processing fidelity, quantum non-locality and less scope for lateral gradients in the emergent Laws of Physics (induced by network defects causing computational errors). On the other hand, such lateral variation in a vast knot network (α) may be essential to the evolution of the Triuniverse, just as variation across the genetic landscape is essential to the evolution of super-emergent Life.
Heuristically, at risk of compromise, both alternatives (α) and (β) may be jointly valid. I suggest the up-scaling pattern best comprises (α) stacked triple sheets in a knot network, in which the knots at the network nodes are (β) triaxial (optical cable-like) super-bundle knots. This combined architecture would provide the Quantum Deep Learning Triuniverse with an up-scaling pattern comprising the benefits of both designs, (α) plus (β), and a functional foundation for a Tensor Neural Knot Network.
I conclude this section with a matrix formalisation of Table 1:
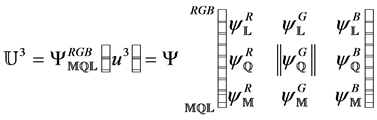 (1)
(1)
where 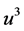 is a prior state of the Triuniverse,
is a prior state of the Triuniverse, 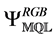 is the macrocycle trefoil evolution operator and
is the macrocycle trefoil evolution operator and 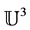 is the subsequently evolved state of the Triuniverse.
is the subsequently evolved state of the Triuniverse.
RGB-tricolour superscripts represent Elemental (R), Operational (G) and Structural (B) phases of the subscripted substrate of Mathematics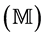 , simulated layer of emergent Physics
, simulated layer of emergent Physics 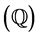 and super-simulated layer of super-emergent Life
and super-simulated layer of super-emergent Life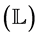 .
.
The right hand side of Equation (1) shows  in expanded form:
in expanded form:
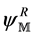 represents the evolution
represents the evolution 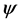 of Algebra in the Elemental (R) information processing loop of the substrate of Mathematics
of Algebra in the Elemental (R) information processing loop of the substrate of Mathematics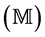 .
. 
























3. Evolution of Algebraic Algorithmic Geometry
I postulate that during the inception of the Triuniverse on the substrate of Mathematics, Elemental (R) Algebra enabled Operational (G) Algorithms, which then enabled Structural (B) Geometry. The order of enablement is irreversible and is a fundamental characteristic of the direction of the evolution of information complexity (parallel to the emergent arrow of time) and to the RGB sequence of loop formation and execution. I put forward this heuristic postulate upon a concept of spontaneous symmetry breaking in which sequential asymmetric algebraic logic, e.g. antisymmetric and irreflexive relations, emerged from primitive non-sequential symmetric logic, e.g. equalities, enabling a new loop of Algebra to emerge and evolve into Algebraic Algorithms.
Algebraic Algorithms then scripted their own self-evolution, through their reinforced- feedback iterations, enabling shapes to be traceable and thus, in another spontaneous new loop, Geometry was subsequently created as Mathematical complexity continued to evolve from primitive logic. The most primitive expression of this new geometry was and still is the triangle, or 2-simplex, which is the fundamental component shape of Quantum Geometrodynamics, or shape dynamics, in emergent Physics (Section §4).
Above it is proposed that Algorithms are modified by evolutionary loop processes. In 1928 Hilbert worked on the “entscheidungs problem” (decision problem) to show that the basic axioms of mathematics are logically consistent and he sought an algorithm that would indicate whether a given mathematical statement could be proved from those axioms alone. Turing [156] showed that there was no such algorithm; indeed there were algorithms that machines would run indefinitely and inconclusively [157] . Consequently we realise though Turing’s work that Algorithms are eternally open to self-evolution. These algorithm evolutions lead to Quantum Deep Learning processes at the kernel of this Triuniverse quantum foundations concept.
As an adjunct conjecture, I propose that there was a corresponding evolution of the dimensionality of quantum information processing. I put forward that the dimensionality spontaneously transitioned from U-bit real-vector-space universal quantum bit processing of Algebra [158] , through qubit processing of complex numbers in Algebraic Algorithms, to enable qutrit processing of Algebraic Algorithmic Geometry.
This conjectured evolution from U-bit, through qubit, to qutrit processing occurred within the first instants of the correspondingly emergent physical Triuniverse. In other words, as Mathematics spontaneously evolved, so did the dimensionality of the quantum computations of the Triuniverse and thus so did the corresponding emergent quantum Physics.
I claim the Triuniverse immediately stabilised as RGB-tricoloured. It did not form any further loops, for a fourth Mathematical phase beyond Algebraic Algorithmic Geometry (and correspondingly not beyond the RGB-tricoloured quantum Physics of Quantum Intelligent Geometrodynamics). I propose this was because the quantum foundations computations are performed with the integer base
The quantum foundations computations are also envisaged to be in the balanced ternary system

I close this section by considering the three processing loops in Algebraic Algorithmic Geometry acting as separate and co-adaptive feedback loops which produce correlations between components within each loop, some of which were previously independent. I claim such feedback produces correlations manifest through correlation systems specific to their hierarchy of emergence. The substrate of Mathematics, upon which Algebraic Algorithmic Geometry executes, is postulated to have a correlation system which is a Tensor Neural Knot Network (see also Khalidi [160] , Orus [161] ) enabling Qutrit Entanglement [154] [162] - [165] .
Therein the Tensors evolve through their algebraic (R) feedback loops, Neural Nodes (Knots) evolve through their feedback loops towards becoming ever more artificially intelligent algorithmic (G) processing nodes, and the Network geometry (B) evolves towards an increasingly efficient Mathematical connectome (Tensor Neural Knot Network enabling Qutrit Entanglement).
Algebra loop-specific correlations develop within the evolving Tensors. Algorithm loop-specific correlations develop within the evolving Neural Nodes (Knots). Geometry loop-specific correlations develop within the evolving Network.
In the trefoil macrocycle, information exchanges occur between the three RGB- tricoloured processes at the “crosstalk node” (ψ), enabling advantageous triplewise co-adaptation and co-evolution of Algebraic Algorithmic Geometry. I propose that this evolution was substantially completed within the first instants at the inception of the Triuniverse. With the substrate of Mathematics thus immediately fully evolved it was directly able to simulate the next layer, that of emergent Physics, which was spontaneously propelled through the apparent “Big Bang” into its evolutionary programme of Quantum Intelligent Geometrodynamics (Section §4).
4. Evolution of Quantum Intelligent Geometrodynamics
The Quantum Deep Learning Triuniverse quantum foundations concept envisages that the evolution of Algebraic Algorithmic Geometry (previous Section §3) occurred on the substrate of Mathematics, which underlies emergent Physics. In this section I discuss the colour-corresponding trefoil macrocycle of emergent Physics as the evolution of Quantum Intelligent Geometrodynamics. I draw upon standard quantum mechanics, the seminal work of Zurek and his co-workers on concepts of einselection and quantum Darwinism [58] - [60] [75] [102] and on the Machian geometrodynamics, or shape dynamics, of spatial and temporal relationalism [103] - [108] . The Operational (G) tri-unifier of these concepts is Quantum Deep Learning [3] [27] [29] [42] through which the Triuniverse appears to self-evolve as if with fine-tuned intelligence. Quantum Deep Learning is highlighted at the centre of the 3 × 3 arrangement of RGB-tricoloured processing loops in Table 1 and Equation (1).
In quantum mechanics, distributions of superposed quantum states evolve according to the Schrödinger equation into linear superpositions of different states, which predicts classically paradoxical dichotomies such as “Schrödinger’s cat”. The algebraic probability density functions of the superposed states are real, or PBR ψ-ontic [166] , but such paradoxical feline dichotomies are evidently not. These algebraic quantum probability density functions and their Schrödinger evolutions correspond to the Elemental (R) information processing loop in emergent quantum Physics and to the homochromatic Algebra loop on the underlying substrate of Mathematics. The possible variations within the algebraic quantum probability density functions also have (R) colour correspondence with variations in classical super-emergent Life, via Darwinism and more deeply via quantum Darwinism. Perhaps pertinently, Gryb [106] also discusses the significance of free endpoint variation in implementing Mach’s Principle using gauge theory in geometrodynamics or shape dynamics.
Algebraic variation is clearly as fundamental in super-emergent Life and in emergent Physics as it is on the substrate of Mathematics. However the RGB-tricolour correspondence throughout the simulated hierarchy of emergence is neither purely quantum mechanical nor purely classical, it is a characteristic Quantum Deep Learning colour correspondence from Algebraic Algorithmic Geometry, through Quantum Intelligent Geometrodynamics to Variational Selective Heredity (Table 1). Whilst the PBR ψ-ontic picture of quantum theory holds [166] there is, within the Quantum Deep Learning Triuniverse concept, also a leading role for RGB-tricoloured deep learning correspondence in the form of advantageous knowledge which accumulates naturally from ψ-Epistemic Drive (Section §2).
Zurek [59] envisages quantum states concurrently having epistemological and ontological roles, and describes quantum states as “epiontic”, due to his quantum information-theoretic union of these two functions. Through this paradigm, ψ-ontic, or reliable classical existence states emerge from the quantum substrate. See also Pusey, Barrett & Rudolph [166] , Colbeck and Renner [167] , Hardy [168] , Patra, Pironio and Massar [169] , Leifer [170] and Gao [171] for discussions on ontological model frameworks. Considering these works, the fundamental framework for everything conjectured in this paper is ψ-epistemic-driven, whilst being ψ-ontic, and so Zurek’s “epiontic” states apply.
The algorithmic selection of hereditable classical realities is well expressed by Zurek’s quantum Darwinism program. Quantum Darwinism proposes that decoherence selects preferred pointer states which survive interaction with the environment. Zurek calls this algorithm “environment-induced superselection”, or “einselection” for short.
These pointer states persist whilst their superpositions decohere and they are localized and effectively classical. Through quantum Darwinism, Zurek proposes that tracing flows of information in our quantum Universe (or Triuniverse) explains why we see the world as classical. Mutual information is the key tool of Zurek’s quantum Darwinism concept. Quantum Darwinism acknowledges that environments comprise many subsystems and observers acquire information about a system of interest by intercepting copies of its pointer states which are output to the environment as a consequence of decoherence.
The quantum system’s interactions with its environment record multiple redundant copies of information about its pointer states and this information is accessible by many observers, thus achieving consensual concurrence on their common information about the quantum state. This enables the colour-corresponding trefoil macrocycle of super-simulated super-emergent Life (next Section §5) to evolve classically within simulated emergent Physics. The multiple redundant copies of information about its pointer states are a form of (geometric) replication, or heredity.
In partial summary; quantum Darwinism exhibits RGB-tricolouration, as per trefoil macrocycle concept definitions above (Section §2). The evolution of algebraic quantum probability density functions of variation occurs in the Elemental (R) processing loop. The evolution of einselection and of the Quantum Deep Learning algorithms occurs in the Operational (G) processing loop. The evolution of multiple copies of information about pointer states occurs in Structural (B) processing loops. Yet there is more to emergent Physics than the correlation system of quantum Darwinism.
The Elemental (R) phase of the emergent Physics trefoil macrocycle is addressed by quantum mechanics with quantum Darwinism. Quantum physics is clearly algebraic. However the Operational (G) phase is only partly addressed by einselection and the Structural (B) phase of the emergent Physics trefoil macrocycle is only partly addressed by pointer state reproductive inheritance.
At this juncture, I therefore crystallise the emerging pattern of this Quantum Deep Learning Triuniverse concept to make a claim to connect a bridge (G) between algebraic physics (R) and geometric physics (B). Thus far in the development of science, algebraic Physics (R) has been explored through quantum mechanics and geometrically dynamic gravitational Physics (B) has been effectively solved by general relativity. I build a bridge (G) with Quantum Deep Learning, which is highlighted at the centre of the 3 × 3 coloured arrangement of processing loops (Table 1 and Equation (1)) and is the kernel of this original quantum foundations concept.
Quantum Deep Learning, I propose, completes the explanation of emergent Physics and I invoke Barbour’s [103] concept of shape dynamics, leading to Quantum Geometrodynamics, to complete the explanation of the Structural (B) loop of emergent Physics, beyond that possible through quantum Darwinism alone.
In other words; from the Red (R), to Green (G), to Blue (B) phases of the trefoil macrocycle in emergent Physics, the Elemental (R) phase is predominantly explained by quantum mechanics, the Operational (G) middle phase is predominantly explained by Quantum Deep Learning and the subsequent Structural (B) phase is predominantly explained by Quantum Geometrodynamics. Notwithstanding this theoretic sequence, I propose that Zurek’s quantum Darwinism transcends the RGB-tricoloured macrocycle of emergent Physics and is applicable in each of the tricoloured phases as a correlation system (Table 1). As effective as it is however, to build a complete picture of emergent Physics we need to complement quantum Darwinism with Elemental (R) Quantum Mechanics, Operational (G) Quantum Deep Learning and Structural (B) Quantum Geometrodynamics.
The trefoil macrocycle of Quantum Intelligent Geometrodynamics simulates the layer of emergent Physics. It is proposed that upon that simulated layer a super-simula- tion of super-emergent Life is enabled and enacted. The trefoil macrocycle in that super-simulation of super-emergent Life (biological and artificial intelligence) is a RGB- tricoloured corresponding trefoil macrocycle of Variational Selective Heredity, which is discussed in the following Section §5.
5. Evolution of Variational Selective Heredity
The three key components of the evolution of Life are variation, selection and heredity [1] . In a major development of Darwin’s seminal concept, Watson and Szathmáry [54] describe how each of these three components is modified by evolutionary loop processes. In the terminology which they adopt, “Evo-Devo” is the evolution of developmental interactions that modify the distribution of phenotypic variation. In the terminology of the Quantum Deep Learning Triuniverse concept, this is an Elemental (R) reinforced-feedback loop process.
“Evo-Eco” in the adopted terminology of Watson and Szathmáry is the evolution of ecological interactions that modify the form of selective pressures. In the terminology of the Quantum Deep Learning Triuniverse concept this is an Operational (G) reinforced-feedback loop process.
“Evo-Ego” in the adopted terminology of Watson and Szathmáry is the evolution of reproductive interactions that modify evolutionary individuality by changing mechanisms of heredity. In the terminology of the Quantum Deep Learning Triuniverse concept this is a Structural (B) reinforced-feedback loop process.
Watson and Szathmáry also highlight, as I do, that such feedback loops are strongly relevant in deep learning systems. The evolution of Life is executed through a deep learning macrocycle. Furthermore, Watson and Szathmáry note that each of these feedback loops results in correlations between components that were previously independent. This is also fundamental to the Quantum Deep Learning Triuniverse concept above.
The correlation ecosystem of Life (Table 1) is beautifully illustrated in the closing section of Darwin’s magnus opus on the origin of species, in which he contemplates an ecologically “Entangled Bank”, as follows [2] :
“It is interesting to contemplate an entangled bank, clothed with many plants of many kinds, with birds singing on the bushes, with various insects flitting about, and with worms crawling through the damp earth, and to reflect that these elaborately constructed forms, so different from each other, and dependent on each other in so complex a manner, have all been produced by laws acting around us. These laws, taken in the largest sense, being Growth with Reproduction; Inheritance which is almost implied by reproduction; Variability from the indirect and direct action of the external conditions of life, and from use and disuse; a Ratio of Increase so high as to lead to a Struggle for Life, and as a consequence to Natural Selection, entailing Divergence of Character and the Extinction of less-improved forms. Thus, from the war of nature, from famine and death, the most exalted object which we are capable of conceiving, namely, the production of the higher animals, directly follows. There is grandeur in this view of life, with its several powers, having been originally breathed into a few forms or into one; and that, whilst this planet has gone cycling on according to the fixed law of gravity, from so simple a beginning endless forms most beautiful and most wonderful have been, and are being, evolved.”
Alas as beautiful as Darwin’s illustration is, I contend super-emergent Life is an illusion, a computational super-simulation upon the simulated layer of emergent Physics, which itself is determined by its underlying substrate of Mathematics. A common triunifying thread woven through these layers is advantageous knowledge which enables out-computation (sic) of alternatives and ψ-Epistemic Drive propels evolution through stacked RGB-tricolour corresponding trefoil macrocycles. In super-simulated super- emergent biological Life the trophic web appears to be bio-energy based, however the RGB-tricoloured corresponding quantum foundations trophic web is information based. Research into the competitive and co-operative dynamics of the bio-energy based trophic web of Life provides insights into those RGB-tricoloured corresponding dynamics in the underlying information based quantum foundations trophic web.
6. Conclusions
I have introduced an original quantum foundations concept of a Quantum Deep Learning Triuniverse. It is a candidate intelligent metaheuristic for the evolution of everything. This triunification concept envisages a triplewise picture of the evolution of the Universe, from its Mathematical substrate, through its computationally simulated layer of emergent Physics, to its super-simulated layer of super-emergent Life (biological and artificial intelligence), with RGB-tricoloured correspondences between these three layers.
The RGB-tricoloured trefoil knot represents a postulated macrocycle topology of triplewise information processing loops. The loop processes execute endlessly in sequence from Red (R), through Green (G), to Blue (B), to Red (R) and so on. The trefoil is a torus knot and the tricoloured processes converge, crosstalk then diverge through the “hole” of the torus at a central “crosstalk node” (ψ).
I consider the trefoil to be a knotted information-conducting (optical-like) fiber. I envisage each of such fibers as a quantum foundational trefoil knot vortex in a ψ-Epistemic Field (the field which produces ψ-Epistemic Drive). ψ-Epistemic Drive is a pervasive Natural appetite for information selected for advantageous knowledge. Selected information is exploited as advantageous knowledge during knowledge-based exploration for further useful information in the harsh environment of an information trophic web. The ψ-Epistemic Field has a landscape of knowledge gradients, with valleys of obliviousness and peaks of insight. Notwithstanding, superposed states are real, or PBR ψ-ontic, so Zurek’s “epiontic” states apply.
The three RGB-tricoloured processing loops each iteratively cause their respective loop processes to evolve. I propose these processing loops act as reinforced-feedback loops which produce correlations between components within that loop, some of which components were previously independent. The trefoil macrocycle evolves in triunity through Quantum Deep Learning, as a consequence of each of its three component feedback loop processes co-evolving with co-adaptation enabled through RGB-crosstalk (ψ) with computational triple-modular-redundancy majority voting.
Unifications are often attempted pairwise which, I suggest, produces a blind spot in quantum foundations research. This unorthodox triplewise triunification offers a new perspective on some of the principal outstanding problems of modern science.
Acknowledgements
This original research is self-funded and I thank my reviewers and editors for their valuable support.
Cite this paper
McCoss, A. (2016) Quantum Deep Learning Triuniverse. Journal of Quantum Information Science, 6, 223- 248. http://dx.doi.org/10.4236/jqis.2016.64015
References
- 1. Darwin, C. (1859) The Origin of Species. Murray, London.
- 2. Van Wyhe, J. (2006) The Complete Work of Charles Darwin Online. Notes and Records of the Royal Society, 60, 87-89.
http://dx.doi.org/10.1098/rsnr.2005.0128 - 3. Wiebe, N., Kapoor, A. and Svore, K.M. (2014) Quantum Deep Learning. Arxiv:1412.3489
- 4. Aldrich, H.E., Hodgson, G.M., Hull, D.L., Knudsen, T., Mokyr, J. and Vanberg, V.J. (2008) In Defence of Generalized Darwinism. Journal of Evolutionary Economics, 18, 577-596.
http://dx.doi.org/10.1007/s00191-008-0110-z - 5. Armstrong, S., Morizur, J.F., Janousek, J., Hage, B., Treps, N., Lam, P.K. and Bachor, H.A. (2012) Programmable Multimode Quantum Networks. Nature Communications, 3, Article No. 1026.
http://dx.doi.org/10.1038/ncomms2033 - 6. Bäck, T., Fogel, D.B. and Michalewicz, Z. (1997) Handbook of Evolutionary Computation. Institute of Physics Pub., Bristol, UK.
- 7. Basu, S., Pollack, R. and Roy, M.F.I. (2003) Algorithms in Real Algebraic Geometry. In: Algorithms and Computation in Mathematics, Springer, Berlin Heidelberg.
http://dx.doi.org/10.1007/978-3-662-05355-3 - 8. Barvinsky, A.O. (1986) Quantum Geometrodynamics: The Wheeler-Dewitt Equations for the Wave Function of the Universe. Physics Letters B, 175, 401-404.
http://dx.doi.org/10.1016/0370-2693(86)90612-X - 9. Bianchi, M., Pradisi, G. and Sagnotti, A. (1992) Toroidal Compactification and Symmetry Breaking in Open-String Theories. Nuclear Physics B, 376, 365-386.
http://dx.doi.org/10.1016/0550-3213(92)90129-Y - 10. Bickhard, M.H. and Campbell, D.T. (2003) Variations in Variation and Selection: The Ubiquity of the Variation-and-Selective-Retention Ratchet in Emergent Organizational Complexity. Foundations of Science, 8, 215-282.
http://dx.doi.org/10.1023/A:1025046917589 - 11. Campbell, J.O. (2016) Universal Darwinism as a Process of Bayesian inference. Frontiers in Systems Neuroscience, 10, 49.
http://dx.doi.org/10.3389/fnsys.2016.00049 - 12. Carroll, S.B. (2008) Evo-Devo and an Expanding Evolutionary Synthesis: A Genetic Theory of Morphological Evolution. Cell, 134, 25-36.
http://dx.doi.org/10.1016/j.cell.2008.06.030 - 13. Champagnat, N., Ferrière, R. and Méléard, S. (2006) Unifying Evolutionary Dynamics: from Individual Stochastic Processes to Macroscopic Models. Theoretical Population Biology, 69, 297-321.
http://dx.doi.org/10.1016/j.tpb.2005.10.004 - 14. Chastain, E., Livnat, A., Papadimitriou, C. and Vazirani, U. (2014) Algorithms, Games, and Evolution. Proceedings of the National Academy of Sciences of the United States of America, 111, 10620-10623.
http://dx.doi.org/10.1073/pnas.1406556111 - 15. Dawkins, R. (1983) Universal Darwinism. In: Bendall, D.S., Ed., Evolution from Molecules to Man, Cambridge University Press, New York.
- 16. Deutsch, D. and Jozsa, R. (1992) Rapid Solution of Problems by Quantum Computation. Proceedings of the Royal Society of London. Proceedings of the Royal Society A: Mathematical and Physical Sciences, 439, 553-558.
http://dx.doi.org/10.1098/rspa.1992.0167 - 17. Dobzhansky, T. (1949) Towards a Modern Synthesis. Evolution, 3, 376-377.
http://dx.doi.org/10.2307/2405724 - 18. Eldredge, N. (1985) Unfinished Synthesis: Biological Hierarchies and Modern Evolutionary Thought. Oxford University Press, New York.
- 19. Flores Martinez, C.L. (2014) SETI in the Light of Cosmic Convergent Evolution. Acta Astronautica, 104, 341-349.
http://dx.doi.org/10.1016/j.actaastro.2014.08.013 - 20. Fogel, D.B. (2006) Evolutionary Computation: Toward a New Philosophy of Machine Intelligence. John Wiley & Sons, Hoboken.
- 21. Georgiev, G. and Georgiev, I. (2002) The Least Action and the Metric of an Organized System. Open Systems & Information Dynamics, 9, 371-380.
http://dx.doi.org/10.1023/A:1021858318296 - 22. Gray, J., He, Y.-H. and Lukas, A. (2006) Algorithmic Algebraic Geometry and Flux Vacua. Journal of High Energy Physics, 2006, 31.
http://dx.doi.org/10.1088/1126-6708/2006/09/031 - 23. Han, K.H. and Kim, J.H. (2002) Quantum-Inspired Evolutionary Algorithm for a Class of Combinatorial Optimization. IEEE Transactions on Evolutionary Computation, 6, 580-593.
http://dx.doi.org/10.1109/TEVC.2002.804320 - 24. Hartshorne, R. (1977) Algebraic Geometry. In: Graduate Texts in Mathematics, Springer, Berkeley, California.
http://dx.doi.org/10.1007/978-1-4757-3849-0 - 25. Hormozi, L., Bonesteel, N.E. and Simon, S.H. (2009) Topological Quantum Computing with Read-Rezayi States. Physical Review Letters, 103, Article ID: 160501.
http://dx.doi.org/10.1103/PhysRevLett.103.160501 - 26. Kiefer, C. (2012) Quantum Geometrodynamics. In: Quantum Gravity, 3rd Edition, Oxford Science Publications, Oxford, 141-189.
http://dx.doi.org/10.1093/acprof:oso/9780199585205.003.0005 - 27. Koutník, J., Cuccu, G., Schmidhuber, J. and Gomez, F. (2013) Evolving Large-Scale Neural Networks for Vision-Based Reinforcement Learning. Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, Amsterdam, 6-10 July 2013, 1061-1068.
http://dx.doi.org/10.1145/2463372.2463509 - 28. Last, C. (2015) Big Historical Foundations for Deep Future Speculations: Cosmic Evolution, Atechnogenesis, and Technocultural Civilization. Foundations of Science, 1-86.
http://dx.doi.org/10.1007/s10699-015-9434-y - 29. LeCun, Y., Bengio, Y. and Hinton, G. (2015) Deep Learning. Nature, 521, 436-444.
http://dx.doi.org/10.1038/nature14539 - 30. Peldán, P. (1996) A Modular Invariant Quantum Theory from the Connection Formulation of (2 + 1)-Gravity on the Torus. Classical and Quantum Gravity, 13, 221-224.
http://dx.doi.org/10.1088/0264-9381/13/2/010 - 31. Peldán, P. (1996) Large Diffeomorphisms in 2 + 1 Quantum Gravity on the Torus. Physical Review D, 53, 3147-3155.
http://dx.doi.org/10.1103/PhysRevD.53.3147 - 32. Marolf, D.M. (1993) Loop Representations for 2 + 1 Gravity on a Torus. Classical and Quantum Gravity, 10, 2625-2647.
http://dx.doi.org/10.1088/0264-9381/10/12/020 - 33. Meusburger, C. and Noui, K. (2010) Combinatorial Quantisation of the Euclidean Torus Universe. Nuclear Physics B, 841, 463-505.
http://dx.doi.org/10.1016/j.nuclphysb.2010.08.014 - 34. Narain, K.S., Sarmadi, M.H. and Witten, E. (1987) A Note on Toroidal Compactification of Heterotic String Theory. Nuclear Physics B, 279, 369-379.
http://dx.doi.org/10.1016/0550-3213(87)90001-0 - 35. Nielsen, M.A. and Chuang, I.L. (2010) Quantum Computation and Quantum Information. 10th Anniversary Edition, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511976667 - 36. Padgett, M.J., O’Holleran, K., Leach, J., Courtial, J. and Dennis, M.R. (2006) The Topology of Vortex Lines in Light Beams. Topology in Ordered Phases. Proceedings of the 1st International Symposium on TOP, Sapporo, 7-10 March 2005, 287-294.
http://dx.doi.org/10.1142/9789812772879_0046 - 37. Pitkänen, M. (2009) Topological Geometrodynamics Inspired Quantum Model of Living Matter. NeuroQuantology, 7, 338-367.
http://dx.doi.org/10.14704/nq.2009.7.3.238 - 38. Powell, R. and Mariscal, C. (2015) Convergent Evolution as Natural Experiment: The Tape of Life Reconsidered. Interface Focus, 5, Article ID: 20150040.
http://dx.doi.org/10.1098/rsfs.2015.0040 - 39. Rickles, D. (2008) Quantum Gravity: A Primer for Philosophers. Ashgate, Aldershot.
- 40. Rovelli, C. and Smolin, L. (1995) Discreteness of Area and Volume in Quantum Gravity. Nuclear Physics B, 442, 593-619.
http://dx.doi.org/10.1016/0550-3213(95)00150-Q - 41. Smolin, L. (2014) Linking Shape Dynamics and Loop Quantum Gravity. Physical Review D, 90, Article ID: 044070. http://dx.doi.org/10.1103/PhysRevD.90.044070
- 42. Schmidhuber, J. (2015) Deep Learning in Neural Networks: An Overview. Neural Networks, 61, 85-117.
http://dx.doi.org/10.1016/j.neunet.2014.09.003 - 43. Smart, J.M. (2009) Evo Devo Universe? A Framework for Speculations on Cosmic Culture. In: Dick, S.J. and Lupisella, M.L., Eds., Cosmos & Culture: Cultural Evolution in a Cosmic Context, Govt Printing Office, NASA SP-2009-4802, Washington DC, 201-295.
- 44. Smolin, L. (1992) Did the Universe Evolve? Classical and Quantum Gravity, 9, 173-191.
http://dx.doi.org/10.1088/0264-9381/9/1/016 - 45. Smolin, L. (1997) The Life of the Cosmos. Oxford University Press, Oxford, USA.
- 46. Smolin, L. (2004) Cosmological Natural Selection as the Explanation for the Complexity of the Universe. Physica A: Statistical Mechanics and Its Applications, 340, 705-713.
http://dx.doi.org/10.1016/j.physa.2004.05.021 - 47. Sterelny, K., Smith, K.C. and Dickison, M. (1996) The Extended Replicator. Biology and Philosophy, 11, 377-403.
http://dx.doi.org/10.1007/BF00128788 - 48. Thiemann, T. (2003) Lectures on Loop Quantum Gravity. In: Giulini. D.J.W., Kiefer, C. and Lämmerzahl, C., Eds., Quantum Gravity, Springer Berlin Heidelberg, 41-135.
http://dx.doi.org/10.1007/978-3-540-45230-0_3 - 49. Valiant, L. (2013) Probably Approximately Correct: Nature’s Algorithms for Learning and Prospering in a Complex World. Basic Books, New York.
- 50. Vidal, C. (2010) Introduction to the Special Issue on the Evolution and Development of the Universe. Foundations of Science, 15, 95-99.
http://dx.doi.org/10.1007/s10699-010-9176-9 - 51. Vidal, C. (2014) The Beginning and the End: The Meaning of Life in a Cosmological Perspective. Springer International Publishing, Switzerland.
http://dx.doi.org/10.1007/978-3-319-05062-1 - 52. Watson, R.A. (2012) Is Evolution by Natural Selection the Algorithm of Biological Evolution? Artificial Life, 13, 121-128.
- 53. Watson, R.A., Mills, R., Buckley, C.L., Kouvaris, K., Jackson, A., Powers, S.T., Cox, C., Tudge, S., Davies, A., Kounios, L. and Power, D. (2015) Evolutionary Connectionism: Algorithmic Principles Underlying the Evolution of Biological Organisation in Evo-Devo, Evo-Eco and Evolutionary Transitions. Evolutionary Biology, 1-29.
http://dx.doi.org/10.1007/s11692-015-9358-z - 54. Watson, R.A. and Szathmary, E. (2016) How Can Evolution Learn? Trends in Ecology & Evolution, 31, 147-157.
http://dx.doi.org/10.1016/j.tree.2015.11.009 - 55. Watson, R.A., Ficici, S.G. and Pollack, J.B. (2002) Embodied Evolution: Distributing an Evolutionary Algorithm in a Population of Robots. Robotics and Autonomous Systems, 39, 1-18.
http://dx.doi.org/10.1016/S0921-8890(02)00170-7 - 56. Wheeler, J.A. (1957) On the Nature of Quantum Geometrodynamics. Annals of Physics, 2, 604-614.
http://dx.doi.org/10.1016/0003-4916(57)90050-7 - 57. Wheeler, J.A. (1968) Superspace and the Nature of Quantum Geometrodynamics. Topics in Nonlinear Physics, 615-724.
- 58. Zurek, W.H. (2003) Decoherence, Einselection, and the Quantum Origins of the Classical. Reviews of Modern Physics, 75, 715-775.
http://dx.doi.org/10.1103/RevModPhys.75.715 - 59. Zurek, W.H. (2003) Quantum Darwinism and Envariance. arXiv:quant-ph/0308163
- 60. Zurek, W.H. (2009) Quantum Darwinism. Nature Physics, 5, 181-188.
http://dx.doi.org/10.1038/nphys1202 - 61. Bousso, R. (2002) The Holographic Principle. Reviews of Modern Physics, 74, 825-874.
http://dx.doi.org/10.1103/RevModPhys.74.825 - 62. ‘t Hooft, G. (2005) The Holographic Mapping of the Standard Model onto the Black Hole Horizon: I. Abelian Vector Field, Scalar Field and BEH Mechanism. Classical and Quantum Gravity, 22, 4179-4188.
http://dx.doi.org/10.1088/0264-9381/22/20/001 - 63. Susskind, L. (1995) The World as a Hologram. Journal of Mathematical Physics, 36, 6377.
http://dx.doi.org/10.1063/1.531249 - 64. Witten, E. (1998) Anti De Sitter Space and Holography. Advances in Theoretical and Mathematical Physics, 2, 253-291.
http://dx.doi.org/10.4310/ATMP.1998.v2.n2.a2 - 65. Myung, Y.S. (2005) Holographic Principle and Dark Energy. Physics Letters B, 610, 18-22.
http://dx.doi.org/10.1016/j.physletb.2005.02.006 - 66. Bekenstein, J.D. (2003) Information in the Holographic Universe. Scientific American, 289, 58-65.
http://dx.doi.org/10.1038/scientificamerican0803-58 - 67. Turing, A.M. (1950) I.—Computing Machinery and Intelligence. Mind, LIX, 433-460.
http://dx.doi.org/10.1093/mind/LIX.236.433 - 68. Shannon, C.E. (1948) A Mathematical Theory of Communication. The Bell System Technical Journal, 27, 379-423.
http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x - 69. Shannon, C.E. (1948) A Mathematical Theory of Communication. The Bell System Technical Journal, 27, 623-656.
http://dx.doi.org/10.1002/j.1538-7305.1948.tb00917.x - 70. Von Neumann, J. (1996) Mathematical Foundations of Quantum Mechanics. Princeton University Press, Princeton.
- 71. Jaynes, E.T. (1957) Information Theory and Statistical Mechanics. Physical Review, 106, 620-630.
http://dx.doi.org/10.1103/PhysRev.106.620 - 72. Landauer, R. (1961) Irreversibility and Heat Generation in the Computing Process. IBM Journal of Research and Development, 5, 183-191.
http://dx.doi.org/10.1147/rd.53.0183 - 73. Zuse, K. (1993) The Computer—My Life. Springer Verlag, New York.
http://dx.doi.org/10.1007/978-3-662-02931-2 - 74. Bekenstein, J.D. (2005) How Does the Entropy/Information Bound Work? Foundations of Physics, 35, 1805-1823.
http://dx.doi.org/10.1007/s10701-005-7350-7 - 75. Blume-Kohout, R. and Zurek, W.H. (2005) A Simple Example of “Quantum Darwinism”: Redundant Information Storage in Many-Spin Environments. Foundations of Physics, 35, 1857-1876.
http://dx.doi.org/10.1007/s10701-005-7352-5 - 76. Deutsch, D. (1997) The Fabric of Reality: The Science of Parallel Universes—and Its Implications. Penguin Books, Penguin.
- 77. Deutsch, D. (2013) Constructor Theory. Synthese, 190, 4331-4359.
http://dx.doi.org/10.1007/s11229-013-0279-z - 78. Esposito, M., Harbola, U. and Mukamel, S. (2009) Nonequilibrium Fluctuations, Fluctuation Theorems, and Counting Statistics in Quantum Systems. Reviews of Modern Physics, 81, 1665.
http://dx.doi.org/10.1103/RevModPhys.81.1665 - 79. Fredkin, E. (1990) An Informational Process Based on Reversible Universal Cellular Automata. Physica D: Nonlinear Phenomena, 45, 254-270.
http://dx.doi.org/10.1016/0167-2789(90)90186-S - 80. Fredkin, E. (2003) An Introduction to Digital Philosophy. International Journal of Theoretical Physics, 42, 189-247.
http://dx.doi.org/10.1023/A:1024443232206 - 81. Freedman, M.H., Larsen, M. and Wang, Z. (2002) A Modular Functor Which Is Universal for Quantum Computation. Communications in Mathematical Physics, 227, 605-622.
http://dx.doi.org/10.1007/s002200200645 - 82. Freedman, M., Kitaev, A., Larsen, M. and Wang, Z. (2003) Topological Quantum Computation. Bulletin of the American Mathematical Society, 40, 31-38.
http://dx.doi.org/10.1090/S0273-0979-02-00964-3 - 83. ‘t Hooft, G. (1999) Quantum Gravity as a Dissipative Deterministic System. Classical and Quantum Gravity, 16, 3263-3279.
http://dx.doi.org/10.1088/0264-9381/16/10/316 - 84. ‘t Hooft, G. (2014) The Cellular Automaton Interpretation of Quantum Mechanics. A View on the Quantum Nature of our Universe, Compulsory or Impossible? arXiv:1405.1548
- 85. Kitaev, A.Y. (2003) Fault-Tolerant Quantum Computation by Anyons. Annals of Physics, 303, 2-30.
http://dx.doi.org/10.1016/S0003-4916(02)00018-0 - 86. Kitaev, A. (2006) Anyons in an Exactly Solved Model and Beyond. Annals of Physics, 321, 2-111.
http://dx.doi.org/10.1016/j.aop.2005.10.005 - 87. Lloyd, S. (2012) The Universe as Quantum Computer. In: Zenil, H., Ed., A Computable Universe: Understanding and Exploring Nature as Computation, World Scientific Publishing, 567-581. http://dx.doi.org/10.1142/9789814374309_0029
- 88. Mandal, D. and Jarzynski, C. (2012) Work and Information Processing in a Solvable Model of Maxwell’s Demon. Proceedings of the National Academy of Sciences of the United States of America, 109, 11641-11645.
http://dx.doi.org/10.1073/pnas.1204263109 - 89. Nayak, C., Simon, S.H., Stern, A., Freedman, M. and Das Sarma, S. (2008) Non-Abelian Anyons and Topological Quantum Computation. Reviews of Modern Physics, 80, 1083-1159. http://dx.doi.org/10.1103/RevModPhys.80.1083
- 90. Ogburn, R.W. and Preskill, J. (1999) Topological Quantum Computation. In: Williams, C.P., Ed., Quantum Computing and Quantum Communications, Springer, Berlin Heidelberg.
- 91. Pekola, J.P. (2015) Towards Quantum Thermodynamics in Electronic Circuits. Nature Physics, 11, 118-123.
http://dx.doi.org/10.1038/nphys3169 - 92. Sagawa, T. and Ueda, M. (2008) Second Law of Thermodynamics with Discrete Quantum Feedback Control. Physical Review Letters, 100, Article ID: 080403.
http://dx.doi.org/10.1103/PhysRevLett.100.080403 - 93. Sau, J.D., Lutchyn, R.M., Tewari, S. and Das Sarma, S. (2010) Generic New Platform for Topological Quantum Computation Using Semiconductor Heterostructures. Physical Review Letters, 104, Article ID: 040502.
http://dx.doi.org/10.1103/PhysRevLett.104.040502 - 94. Schmidhuber, J. (2000) Algorithmic Theories of Everything. arXiv:quant-ph/0011122
- 95. Toyabe, S., Sagawa, T., Ueda, M., Muneyuki, E. and Sano, M. (2010) Experimental Demonstration of Information-to-Energy Conversion and Validation of the Generalized Jarzynski Equality. Nature Physics, 6, 988-992.
http://dx.doi.org/10.1038/nphys1821 - 96. Wang, Z. (2010) Topological Quantum Computation. CBMS Regional Conference Series in Mathematics.
- 97. von Weizsäcker, C.F., Görnitz, T. and Lyre, H. (2006) The Structure of Physics. Springer, The Netherlands.
- 98. Wheeler, J.A. (1990) Information, Physics, Quantum: The Search for Links. The Proceedings of the 1988 Workshop on Complexity, Entropy, and the Physics of Information, May-June 1989, Westview Press, Santa Fe, New Mexico, Boulder, CO, USA.
- 99. Wolfram, S. (2002) A New Kind of Science. Wolfram Media, Champaign.
- 100. Zenil, H. (2013) A Computable Universe: Understanding and Exploring Nature as Computation. World Scientific, Hackensack, New Jersey.
- 101. Zizzi, P.A. (2006) Space-Time at the Planck Scale: The Quantum Computer View. In: Garola, C., Rossi, A. and Sozzo, S., Eds., The Foundations of Quantum Mechanics, World Scientific Publishing, 345-358.
http://dx.doi.org/10.1142/9789812773258_0030 - 102. Zurek, W.H. (2007) Relative States and the Environment: Einselection, Envariance, Quantum Darwinism, and the Existential Interpretation. Arxiv:0707.2832.
- 103. Barbour, J.B. (1974) Relative-Distance Machian Theories. Nature, 249, 328-329.
http://dx.doi.org/10.1038/249328a0 - 104. Barbour, J. (2003) Scale-Invariant Gravity: Particle Dynamics. Classical and Quantum Gravity, 20, 1543-1570.
http://dx.doi.org/10.1088/0264-9381/20/8/310 - 105. Barbour, J.B. and Bertotti, B. (1982) Mach’s Principle and the Structure of Dynamical Theories. Proceedings of the Royal Society A: Mathematical and Physical Sciences, 382, 295-306.
http://dx.doi.org/10.1098/rspa.1982.0102 - 106. Gryb, S. (2009) Implementing Mach’s Principle Using Gauge Theory. Physical Review D, 80, Article ID: 024018.
http://dx.doi.org/10.1103/PhysRevD.80.024018 - 107. Gomes, H., Gryb, S. and Koslowski, T. (2011) Einstein Gravity as a 3D Conformally Invariant Theory. Classical and Quantum Gravity, 28, Article ID: 045005.
http://dx.doi.org/10.1088/0264-9381/28/4/045005 - 108. Barbour, J., Koslowski, T. and Mercati, F. (2014) Identification of a Gravitational Arrow of Time. Physical Review Letters, 113, Article ID: 181101.
http://dx.doi.org/10.1103/PhysRevLett.113.181101 - 109. Carlip, S. (1998) Quantum Gravity in 2 + 1 Dimensions. Cambridge University Press, Cambridge.
- 110. Thomson, W. and Kelvin, L. (1867) On Vortex Atoms. Proceedings of the Royal Society of Edinburgh, VI, 94-105. (Reprinted in Philosophical Magazine, XXXIV, 15-24)
- 111. Arias, K.I., Zysman-Colman, E., Loren, J.C., Linden, A. and Siegel, J.S. (2011) Synthesis of a D3-Symmetric “Trefoil” Knotted Cyclophane. Chemical Communications, 47, 9588-9590.
http://dx.doi.org/10.1039/c1cc11209k - 112. Atiyah, M. (1995) Quantum Physics and the Topology of Knots. Reviews of Modern Physics, 67, 977-981.
http://dx.doi.org/10.1103/RevModPhys.67.977 - 113. Berry, M. (2001) Knotted Zeros in the Quantum States of Hydrogen. Foundations of Physics, 31, 659-667. http://dx.doi.org/10.1023/A:1017521126923
- 114. Bilson-Thompson, S., Hackett, J. and Kauffman, L.H. (2009) Particle Topology, Braids, and Braided Belts. Journal of Mathematical Physics, 50, Article ID: 113505.
http://dx.doi.org/10.1063/1.3237148 - 115. Bonesteel, N.E., Hormozi, L., Zikos, G. and Simon, S.H. (2005) Braid Topologies for Quantum Computation. Physical Review Letters, 95, Article ID: 140503.
http://dx.doi.org/10.1103/PhysRevLett.95.140503 - 116. Dennis, M.R., King, R.P., Jack, B., O’Holleran, K. and Padgett, M.J. (2010) Isolated Optical Vortex Knots. Nature Physics, 6, 118-121.
http://dx.doi.org/10.1038/nphys1504 - 117. Dimofte, T. (2013) Quantum Riemann Surfaces in Chern-Simons Theory. Advances in Theoretical and Mathematical Physics, 17, 479-599.
http://dx.doi.org/10.4310/ATMP.2013.v17.n3.a1 - 118. Evans, M.E., Robins, V. and Hyde, S.T. (2015) Ideal Geometry of Periodic Entanglements. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 471, Article ID: 20150254.
http://dx.doi.org/10.1098/rspa.2015.0254 - 119. Faddeev, L. and Niemi, A.J. (1997) Stable Knot-Like Structures in Classical Field Theory. Nature, 387, 58-61.
http://dx.doi.org/10.1038/387058a0 - 120. Faddeev, L. and Niemi, A.J. (1999) Partially Dual Variables in SU(2) Yang-Mills Theory. Physical Review Letters, 82, 1624-1627.
http://dx.doi.org/10.1103/PhysRevLett.82.1624 - 121. Finkelstein, R.J. (2013) The Preon Sector of the SLq(2) Model and the Binding Problem. International Journal of Modern Physics A, 29, Article ID: 1450092.
http://dx.doi.org/10.1142/S0217751X14500924 - 122. Finkelstein, R.J. (2015) The SLq(2) Extension of the Standard Model. International Journal of Modern Physics A, 30, Article ID: 1530037.
http://dx.doi.org/10.1142/S0217751X15300379 - 123. Finkelstein, R.J. and Cadavid, A.C. (2006) Masses and Interactions of q-Fermionic Knots. International Journal of Modern Physics A, 21, 4269-4302.
http://dx.doi.org/10.1142/S0217751X06032496 - 124. Gambini, R., Lewandowski, J., Marolf, D. and Pullin, J. (1998) On the Consistency of the Constraint Algebra in Spin Network Quantum Gravity. International Journal of Modern Physics D, 7, 97-109.
http://dx.doi.org/10.1142/S0218271898000103 - 125. Garnerone, S., Marzuoli, A. and Rasetti, M. (2006) Quantum Knitting. Laser Physics, 16, 1582-1594. http://dx.doi.org/10.1134/S1054660X06110120
- 126. Garoufalidis, S., Morton, H. and Vuong, T. (2013) The SL3 Colored Jones Polynomial of the Trefoil. Proceedings of the American Mathematical Society, 141, 2209-2220.
http://dx.doi.org/10.1090/S0002-9939-2013-11582-0 - 127. Gelca, R. (2002) Non-Commutative Trigonometry and the A-Polynomial of the Trefoil Knot. Mathematical Proceedings of the Cambridge Philosophical Society, 133, 311-323.
- 128. Jehle, H. (1981) Topological Characterization of Leptons, Quarks and Hadrons. Physics Letters B, 104, 207-211.
http://dx.doi.org/10.1016/0370-2693(81)90592-X - 129. Katritch, V., Bednar, J., Michoud, D., Scharein, R.G., Dubochet, J. and Stasiak, A. (1996) Geometry and Physics of Knots. Nature, 384, 142-145.
http://dx.doi.org/10.1038/384142a0 - 130. Kauffman, L.H. (2001) Knots and Physics. World Scientific, Singapore.
- 131. Kauffman, L.H. (2015) Rotational Virtual Knots and Quantum Link Invariants. Journal of Knot Theory and Its Ramifications, 24, Article ID: 1541008.
http://dx.doi.org/10.1142/S0218216515410084 - 132. Kauffman, L.H. (2015) Knot Logic: Logical Connection and Topological Connection. Arxiv:1508.06028
- 133. Kauffman, L.H. (2016) Knot Logic and Topological Quantum Computing with Majorana Fermions. In: Chubb, J., Eskandarian, A. and Harizanov, V., Eds., Logic and Algebraic Structures in Quantum Computing, Lecture Notes in Logic Vol. 45, Cambridge University Press, Cambridge, 223-336.
http://dx.doi.org/10.1017/CBO9781139519687.012 - 134. Kauffman, L.H. and Lomonaco Jr., S.J. (2002) Quantum Entanglement and Topological Entanglement. New Journal of Physics, 4, 73.
http://dx.doi.org/10.1088/1367-2630/4/1/373 - 135. Kauffman, L.H. and Lomonaco Jr., S.J. (2004) Braiding Operators are Universal Quantum Gates. New Journal of Physics, 6, 134.
http://dx.doi.org/10.1088/1367-2630/6/1/134 - 136. Kauffman, L.H. and Lomonaco Jr., S.J. (2004) Quantum Knots. Proceedings of SPIE 5436, Quantum Information and Computation II, 268.
http://dx.doi.org/10.1117/12.544072 - 137. Kleckner, D. and Irvine, W.T.M. (2013) Creation and Dynamics of Knotted Vortices. Nature Physics, 9, 253-258.
http://dx.doi.org/10.1038/nphys2560 - 138. Liu, X. and Ricca, R.L. (2016) Knots Cascade Detected by a Monotonically Decreasing Sequence of Values. Scientific Reports, 6, Article No. 24118.
http://dx.doi.org/10.1038/srep24118 - 139. Moffatt, H.K. (1996) Pulling the Knot Tight. Nature, 384, 114.
http://dx.doi.org/10.1038/384114a0 - 140. Pieranski, P. and Przybyl, S. (2001) Ideal Trefoil Knot. Physical Review E, 64, Article ID: 031801.
http://dx.doi.org/10.1103/PhysRevE.64.031801 - 141. Ponnuswamy, N., Cougnon, F.B., Clough, J.M., Pantos, G.D. and Sanders, J.K. (2012) Discovery of an Organic Trefoil Knot. Science, 338, 783-785.
http://dx.doi.org/10.1126/science.1227032 - 142. Ranada, A.F. (1990) Knotted Solutions of the Maxwell Equations in Vacuum. Journal of Physics A: Mathematical and General, 23, L815-L820.
http://dx.doi.org/10.1088/0305-4470/23/16/007 - 143. Sawin, S. (1996) Links, Quantum Groups and TQFTs. Bulletin of the American Mathematical Society, 33, 413-446.
- 144. Stasiak, A., Dubochet, J., Katritch, V. and Pieranski, P. (1998) Ideal Knots and Their Relation to the Physics of Real Knots. In: Kauffman, L.H., Ed., Series on Knots and Everything, Vol. 19, World Scientific Publishing, 1-19.
http://dx.doi.org/10.1142/9789812796073_0001 - 145. Tempone-Wiltshire, S.J., Johnstone, S.P. and Helmerson, K. (2016) Optical Vortex Knots— One Photon at a Time. Scientific Reports, 6, Article No. 24463.
http://dx.doi.org/10.1038/srep24463 - 146. Thompson, A., Swearngin, J. and Bouwmeester, D. (2014) Linked and Knotted Gravitational Radiation. Journal of Physics A: Mathematical and Theoretical, 47, Article ID: 355205.
http://dx.doi.org/10.1088/1751-8113/47/35/355205 - 147. Was, Z. (1998) Trefoil Knot and Ad-Hoc Classification of Elementary Fields in the Standard Model. Physics Letters B, 416, 369-372.
http://dx.doi.org/10.1016/S0370-2693(97)01346-4 - 148. Weisstein, E.W. (2016) Trefoil Knot. From Mathworld—A Wolfram Web Resource.
http://mathworld.wolfram.com/TrefoilKnot.html - 149. Simon, S. (2010) Quantum Computing with a Twist. Physics World, 23, 35-40.
http://dx.doi.org/10.1088/2058-7058/23/09/37 - 150. Lyons, R.E. and Vanderkulk, W. (1962) The Use of Triple-Modular Redundancy to Improve Computer Reliability. IBM Journal of Research and Development, 6, 200-209.
http://dx.doi.org/10.1147/rd.62.0200 - 151. Griffiths, R.B. (2007) Types of Quantum Information. Physical Review A, 76, Article ID: 062320.
http://dx.doi.org/10.1103/PhysRevA.76.062320 - 152. Perez, J., Füzfa, A., Carletti, T., Mélot, L. and Guedezounme, L. (2014) The Jungle Universe: Coupled Cosmological Models in a Lotka-Volterra Framework. General Relativity and Gravitation, 46, 1753.
http://dx.doi.org/10.1007/s10714-014-1753-8 - 153. Leach, J., Dennis, M.R., Courtial, J. and Padgett, M.J. (2005) Vortex Knots in Light. New Journal of Physics, 7, 55.
http://dx.doi.org/10.1088/1367-2630/7/1/055 - 154. Caves, C.M. and Milburn, G.J. (2000) Qutrit Entanglement. Optics Communications, 179, 439-446.
http://dx.doi.org/10.1016/S0030-4018(99)00693-8 - 155. McConnell, R., Zhang, H., Hu, J., Cuk, S. and Vuletic, V. (2015) Entanglement with Negative Wigner Function of Almost 3,000 Atoms Heralded by One Photon. Nature, 519, 439-442.
http://dx.doi.org/10.1038/nature14293 - 156. Turing, A.M. (1937) On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, s2-42, 230-265.
http://dx.doi.org/10.1112/plms/s2-42.1.230 - 157. Dyson, G. (2012) Turing Centenary: The Dawn of Computing. Nature, 482, 459-460.
http://dx.doi.org/10.1038/482459a - 158. Aleksandrova, A., Borish, V. and Wootters, W.K. (2013) Real-Vector-Space Quantum Theory with a Universal Quantum Bit. Physical Review A, 87, Article ID: 052106.
http://dx.doi.org/10.1103/PhysRevA.87.052106 - 159. Garcia-Morales, V. (2015) Quantum Mechanics and the Principle of Least Radix Economy. Foundations of Physics, 45, 295-332.
http://dx.doi.org/10.1007/s10701-015-9865-x - 160. Khalidi, M.A. (2015) Natural Kinds as Nodes in Causal Networks. Synthese, 1-18.
http://dx.doi.org/10.1007/s11229-015-0841-y - 161. Orús, R. (2014) A Practical Introduction to Tensor Networks: Matrix Product States and Projected Entangled Pair States. Annals of Physics, 349, 117-158.
http://dx.doi.org/10.1016/j.aop.2014.06.013 - 162. Goyal, S.K., Simon, B.N., Singh, R. and Simon, S. (2011) Geometry of the Generalized Bloch Sphere for Qutrit. arXiv:1111.4427
- 163. Klimov, A.B., Guzmán, R., Retamal, J.C. and Saavedra, C. (2003) Qutrit Quantum Computer with Trapped Ions. Physical Review A, 67, Article ID: 062313.
http://dx.doi.org/10.1103/PhysRevA.67.062313 - 164. Li, B., Yu, Z.H. and Fei, S.M. (2013) Geometry of Quantum Computation with Qutrits. Scientific Reports, 3, Article No. 2594.
http://dx.doi.org/10.1038/srep02594 - 165. Sarbicki, G. and Bengtsson, I. (2012) Dissecting the Qutrit. Journal of Physics A: Mathematical and Theoretical, 46, Article ID: 035306.
http://dx.doi.org/10.1088/1751-8113/46/3/035306 - 166. Pusey, M.F., Barrett, J. and Rudolph, T. (2012) On the Reality of the Quantum State. Nature Physics, 8, 475-478.
http://dx.doi.org/10.1038/nphys2309 - 167. Colbeck, R. and Renner, R. (2012) Is a System’s Wave Function in One-to-One Correspondence with Its Elements of Reality? Physical Review Letters, 108, Article ID: 150402.
http://dx.doi.org/10.1103/PhysRevLett.108.150402 - 168. Hardy, L. (2013) Are Quantum States Real? International Journal of Modern Physics B, 27, Article ID: 1345012.
http://dx.doi.org/10.1142/S0217979213450124 - 169. Patra, M.K., Pironio, S. and Massar, S. (2013) No-Go Theorems for Psi-Epistemic Models Based on a Continuity Assumption. Physical Review Letters, 111, Article ID: 090402.
http://dx.doi.org/10.1103/PhysRevLett.111.090402 - 170. Leifer, M.S. (2014) Is the Quantum State Real? An Extended Review of Ψ-Ontology Theorems. Quanta, 3, 67-155.
http://dx.doi.org/10.12743/quanta.v3i1.22 - 171. Gao, S. (2015) An Argument for Ψ-Ontology in Terms of Protective Measurements. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 52, 198-202.
http://dx.doi.org/10.1016/j.shpsb.2015.07.006





