Journal of Quantum Information Science
Vol.06 No.03(2016), Article ID:69700,38 pages
10.4236/jqis.2016.63012
Undulatory Theory with Paraconsistent Logic (Part I): Quantum Logical Model with Two Wave Functions
João Inácio Da Silva Filho
Laboratory of Applied Paraconsistent Logic, Santa Cecilia University, Santos, Brazil

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 7, 2016; Accepted: August 9, 2016; Published: August 12, 2016
ABSTRACT
Paraconsistent logic (PL) is a non-classical logic that accepts contradiction in its foundations. It can be represented in the form of paraconsistent annotated logic with annotation of two values (PAL2v). When used to model quantum phenomena, PAL2v is called paraquantum logic (PQL). In this work, the concept of PQL is applied to create a logical model presenting the fundamental principles of quantum mechanics that support particle-wave theory. This study uses the well-known Young’s double-slit experiment, wherein quantum phenomena appear when a monochromatic light beam passes through the two slits. We focused on a reference point located between the slits, where we observed the effects of two types of wave interferences in a region defined as a two-wave region (2W region). Considering that the effect in this 2W region is very similar to that studied by Huygens, we adopt a paraquantum logical model in which a particle (or quantum) is represented by two wave functions. The two wave functions result in four State Vectors (Ket, Bra, ⌐Ket, ⌐Bra) in the PQL Lattice that express the symmetry and the entanglement of Quantum Mechanics. The constructed model adapts well to the quantum phenomena, is strongly consistent, and can be considered as an innovative form of analysis in the field of quantum mechanics. Based on this model, we present in two parts (Part I and Part II) the comparative analysis of values found in Schrödinger’s equation and probabilistic models of wave-particle theory using Bonferroni inequality.
Keywords:
Paraconsistent Logic, Quantum Mechanics, Paraquantum Logic, Undulatory Theory, Quantum Model

1. Introduction
By the end of the 17th century, several scientists supported the wave theory of light that affirmed the pure wave character of light. However, Newton’s corpuscular theory describing light as a particle already existed and was well accepted within the scientific community [1] . In 1801, the English physicist and physician Thomas Young demonstrated the phenomena of interference of light with solid experimental results that further supported the wave theory of light [2] . It was found that, while light appeared to behave as a particle flow, there were cases where it exhibited wave characteristics, such as in an interference phenomenon. This contradiction between corpuscular and wave theory was addressed by other scholars, culminating in the development of quantum mechanics from 1900 to 1925 [3] . One of the most important theories in Physics today, quantum mechanics has its main concepts based on postulates of difficult adaptability to the classical models observed in our Newtonian reality [3] [4] .
1.1. Paraconsistent Logic (PL)
Classical or Aristotelian logic, which today supports our technology, was created in ancient Greece as a tool to describe a perfect world; its strictly binary laws exclude situations that occur in reality, such as contradictory, incomplete, or uncertain information. Over time, an alternative logic to the classical logic, known as non-classical logic, was developed for obtaining models that better suited such situations. Therefore, non-clas- sical logics oppose the rigid binary laws that support classical logic and were created to better express our reality, especially at measurement limits and borders where, for various reasons, ambiguous, contradictory, and incomplete values render the classical logic inoperative. Among non-classical, non-binary logics, paraconsistent logic (PL) has shown to be promising for applications in physical science.
The precursors of Paraconsistent Logic are the Polish logician J. Lukasiewicz and the Russian philosopher N.A. Vasilev that independently suggested the possibility of a logic that restricts, for example, the principle of contradiction [5] . The initial systems of Paraconsistent Logic containing all logical levels, involving propositional calculations, of predicate and descriptions, as well as logic from superior order are due to N. C. A. Da Costa (1954 onwards) [6] - [8] .
1.2. Paraconsistent Logic Definitions
In formal way [5] [8] , we can define Paraconsistent Logic as any deductive theory. T is based on a given logic L, and we suppose that all logics considered here contain a connective for negation, symbolized. If two formulas of the language of T, one of which is the negation of the other, are both theorems of T (i.e. for some formula A, both A and Aare theorems of T), then T is said to be inconsistent, otherwise T is consistent. If all formulas of the language of T (or all closed formulas) are theorems of T, then T is called trivial; otherwise it is said to be non-trivial. A logic L is paraconsistent if it can be the underlying logic of inconsistent, but non-trivial theories. If the theory T is inconsistent and non-trivial, then T is called a paraconsistent theory [5] [8] . The usual systems of logic, for instance classical and intuitionistic logics, are not paraconsistent.
As shown in [5] [6] , PL’s main characteristic is its revocation of the classical logic principle of non-contradiction, allowing it to deal with inconsistencies without trivialization. Further, we will show that PL can be applied to the analysis of physical systems via a special setting called the paraconsistent annotated logic (PAL) [6] - [8] .
The aim of this paper is to present a new way of modeling quantum mechanics concepts in its wave-particle theory through the PL, a non-classical logic that tolerates contradictions in its foundations. To this effect, we present a model supported by Young’s double-slit experiment, where quantum phenomena appear when a monochromatic light beam is focused on two slits [9] .
We applied Huygens’ principle―proposed in the late 17th century by Christiaan Huygens as the wavefront method―where every point on a wavefront may be considered as a source of elementary waves that propagate at the same frequency beyond the region previously hit by the original wave [2] [4] . In the double-slit experiment, we highlighted a reference point located between the two slits where the effects of two types of wave interference are observed in a region defined as a two-wave region (2W region). The later resulted in a paraquantum logical model, where a particle or quantum is represented by two wave functions.
The first of part of our work is described below.
In Section 2, we present the fundamental principles of paraconsistent annotated logic with annotation of two values (PAL2v) for applications in physical phenomena, called paraquantum logic (PQL), from which a logic model is derived. In Section 3, we show the study and interpretation of Young’s experience and the relation of equations on the phenomena of wave interferences. As a result, we obtain equations of PQL evidence degree and a paraquantum logical model for quantum. In Section 4, we study the quantum paraquantum logical model in one spatial dimension using quantum mechanics concepts. In Section 5, we elaborate conclusions about the obtained model. In Part II, we test this model in relation to Schrödinger’s equation values and compare values using both probability theory and Bonferroni inequality.
2. Paraconsistent Annotated Logic with Annotation of Two Values (PAL2v)
Paraconsistent Logic (PL) is a propositional and evidential non-classical logic which revokes the principle of non-contradiction and admits the treatment of contradictory signals in its theoretical structures [5] . The characteristics of an evidential logic are suitable for treating Uncertain Knowledge, mainly because, in an analysis, the argumentations are restrained to assert that the premises constitute only partial evidences for their conclusions [6] .
When used to model quantum phenomena, the Paraconsistent Logic (PL) is called paraquantum logic (PQL) [10] - [14] . PQL is based on a special type of PL called Para- consistent Annotated Logic with annotation of two values (PAL2v). Based on these considerations, we present PAL2v and the basics of paraquantum logical model [15] .
The paraconsistent annotated logic (PAL) is an evidential logic (ετ) that can be represented by a lattice of four vertices (Lattice FOUR) [7] [8] . Intuitively, the annotation constant in its vertex provides the connotation of the logical state related to proposition P [10] .
An atomic proposition of PAL logic language can be represented by P(μ, λ), where μ and λ are elements in a closed interval [0, 1] belonging to a set of real numbers. When applied, these two values are considered information signals and represent evident measures of proposition P, thus called evidence Degree. Among several intuitive readings, P(μ, λ) can be read as (μ), a favorable evidence to proposition P, and λ, an unfavorable evidence to it. Therefore, the annotation represented in the lattice associated to PAL2v is formed by pairs of values (μ, λ) [10] [11] . Each degree of evidence is extracted from different sources and independent, but both sources are related to the same proposition P, and are therefore considered as Observable Variables in the physical world [8] .
In this representation, an operator is fixed ~: |τ| → |τ| where: t = {(m, λ)|m, λ Î [0, 1]} Ì Â.
The pair consisted of favorable evidence Degree (μ) and unfavorable evidence Degree (λ) provides logic connotation to proposition P [5] [8] - [10] .
For the PAL2v Lattice, extreme logical states represented in the four vertices are: True (t), False (F), Inconsistent (T), and Undetermined (┴). Additionally, the equidistant point between vertices is considered an undefined logical state (I). Figure 1 illustrates the PAL2v lattice with logical states represented by each of its four vertices related to pair values, favorable evidence Degree (μ) and unfavorable evidence Degree (λ).
2.1. Paraconsistent Transformations
Paraconsistent Transformations (PT) are linear transformations conducted between a Unitary Square in the Cartesian Plane USCP-Lattice κ (Figure 2(a)) and another lattice similar to a four-vertex PAL2v (PAL2v-τ Lattice). Through PTs, logic values represented
Figure 1. Lattice FOUR with PAL2v logical states (Hasse Diagram).
Figure 2. (a) Unit square on Cartesian plane USCP―Lattice κ; (b) Scale expansion with 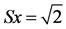 and
and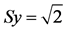 .
.
in PAL2v-τ Lattice can be obtained from USCP-Lattice κ [10] [11] . Three stages are required to obtain paraconsistent transformations: 1) scale expansion, 2) rotation; 3) axis y rotation [11] .
2.1.1. Expansion
Expansion consists of a scale change that allows resizing objects from a reference point.
Consider point P(x, y) and P'(X, Y) as being point coordinates after scaling. Scaling entails multiplying each point Pi of an object by both a horizontal (Sx) and a vertical (Sy) scale factor.
Function T is defined as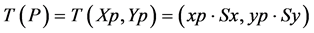 .
.
In paraconsistent transformations, scale is increased in USCP-Lattice κ, as shown in Figure 2, so that: 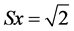 and
and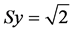 . Therefore, with:
. Therefore, with:  and
and , the scale increase of USCP-Lattice κ is given by the first transformation:
, the scale increase of USCP-Lattice κ is given by the first transformation:
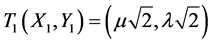 (1)
(1)
From Equation (1) we have: 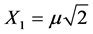 and
and 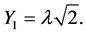
2.1.2. Rotation
The mathematical expression for an object’s rotation from its origin to angle θ, is considered from a point P(xp, yp), such as the point P’(Xp, Yp) is obtained by:
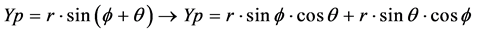 .
.
Function T can thus be defined as follows:
Figure 3 shows a 45˚ rotation in relation to the origin.
For paraconsistent transformation, 45˚ rotation is made in the USCP-Lattice κ from its origin, therefore:
 (2)
(2)
Figure 3. (a) Expanded Lattice; (b) 45˚ Rotation from origin.
From Equation (2) we have:

For a 45˚ rotation:

From Equation (1), we have:






2.1.3. Translation
Consider a geometric object represented by a set of points Pi belonging to R2. The translation is made by adding all quantities to the coordinates. With a translation performed from a point P(x, y) and P’ being the point coordinates after translation, function T is defined as follows:
where: total amounts are dx and dy.
For paraconsistent transformations, a translation in USCP-Lattice κ is made on its axis y, as follows:


With: 


Therefore, 

Equation (4) converts USCP-Lattice κ points into PAL2v τ Lattice points (Hasse diagram), which also represents the lattice associated with PQL [10] [12] . Figure 4 shows the steps needed for this last paraconsistent transformation.
Figure 4. (a) Rotation around origin (45˚); (b) Translation, Lattice is associated with PAL2v.
The first term X3 of the ordered pair obtained in the final transformation represented in Equation (4) is called certainty degree (DC), and calculated by:

where: μ is a Favorable evidence Degree.
λ is an Unfavorable evidence Degree.
Their values belong to a set of real numbers Â, vary in the closed interval −1 to +1, and are located on the horizontal axis of the PAL2v Lattice τ, called Certainty Degree Axis [4] .
The second term Y3 obtained in the ordered pair of the final transformation Equation (4) is called contradiction degree (Dct), and is calculated by:

Values resulted from Dct belong to a set of real numbers Â, vary in the closed interval +1 and −1, and are located on the vertical axis of the PAL2v Lattice τ, called Contradiction Degrees Axis [10] .
In the Lattice τ of the PAL2v, when DC equals +1, the Paraconsistent logical state (ετ) resulting from the Paraconsistent analysis is True (t); when DC equals −1, the logical state is False (F). Likewise, if Dct equals +1, the Paraconsistent logical state (ετ) resulting from the Paraconsistent analysis is inconsistent (T), and if Dct equals −1, it is Undetermined (⊥).
Paraconsistent transformations establish two paraconsistent mathematical operators for measurements of the observable physical environment [10] [12] . The first, 

The performance of both Operators on Observable measurements of the physical world allows standardization and containment in a [0, 1] interval of measurements taken from real numbers.
With geometric change introduced through paraconsistent transformations, values formerly represented by two-dimension Unitary Squares are now represented in one- dimension Open Unitary Square on the Cartesian Plane (USCP Open), where its representative line separates the physical world from the paraconsistent universe (see Figure 5).
2.2. Logical Negation
In PAL2v annotation, the first evidence Degree is represented by μ, which favors proposition P, and the second evidence Degree is represented by λ, which is unfavorable to preposition P. Therefore, the logical negation is achieved by changing evidence Degrees in annotation [4] [6] such that:

Through Equation (5) and Equation (9) we observe that the effect of the Logic Negation Operator on the Lattice of the PAL2v is the change in sign of the Certainty Degree (DC).
2.3. Logical Reversibility Property
Another important application of logic models in quantum mechanics is PAL2v’s reversibility [10] [11] . From the Certainty Degree (DC) and the Contradiction Degree (Dct), we obtain each annotation values represented by a pair, Favorable evidence Degree (μ) and Unfavorable evidence Degree (λ). This is done as follows:
From Equation (5) and Equation (6) we obtain the system
Figure 5. PAL2v lattice with values and line separates the physical world from the paraconsistent universe.
Solving S1, we obtain evidence Degree from both Certainty and Contradiction Degrees:

and

Paraconsistent transformations can then convert Lattice of the PAL2v annotations into USCP annotations. With Equation (5) and Equation (6) it is possible to relate physical environment measurements to behaviors of logical states of the Lattice of the PAL2v, the paraconsistent universe.
The reversibility of PAL2v expressed by Equation (8) and Equation (9) allows, through behaviors predicted from logical states in the Paraconsistent Universe, the forecast of amplitude values represented in USCP. They are obtained from Observable measurements in the physical world and for our study we will name Paraconsistent logic (PAL2v) of Paraquantum Logic (PQL). Figure 6 depicts reversibility conditions of PQL.
3. Paraquantum Logic and Wave Theory
A paraquantum logical state (ψ) is created in the Lattice of the PQL as a pair of values formed by a certainty degree (DC) and contradiction degree (Dct). Both values depend on measurements of variables observed in the physical environment, represented by μ and λ.
Equation (5) and Equation (6) can be can expressed in terms of μ and λ, obtaining a paraquantum logical state (ψ) [11] - [14] such as

Figure 6. Conversion of values between USCP and Lattice of the PQL.
For each measurement of μ and λ conducted in the physical world, we obtain a single pair 
We can represent the Vector of State P(ψ) in a Lattice of the PQL, with its origin in one of the two vertices that compose the horizontal axis of Certainty Degrees. In the vertex of the Vector of State P(ψ), we have a point formed by the pair indicated by the paraquantum function [13] - [15] .
Vector of State P(ψ) will always be equal to the sum of its two vectors:


Given a paraquantum logical state (ψcur) defined by the pair

where: 

Figure 7 shows the point (DCψ, Dctψ) where 

In the Lattice of the PQL, the angle formed by the module of Vector of State M(ψ) and axis x of the Certainty Degree is equal to the Vector of State inclination angle (αψ), which is calculated by:
Figure 7. Vector of state P(ψ) representing a paraquantum logical state (ψ) on the paraquantum Lattice of states on point (DCψ, Dctψ). Therefore, DC > 0.

and:


The increase or decrease of the inclination angle αψ triggers the appearance of logical states along the vertex of Vector of State P(ψ) within the limits of the PQL Lattice. We may say that these paraquantum logical states are superposed (ψsup) [13] - [15] .
When the Vector of State P(ψ) has a unit module (MP(ψ) = 1), the superposed paraquantum logical states have a defined trajectory in which the logical state will be at the equidistant lattice point given a null inclination angle, with Certainty and contradiction degrees equals to zero.
3.1. Wave Interferences
The wave theory of light resulted in several studies that relate wave interference phenomena with phenomena that occur in quantum mechanics. We will use quantum phenomena information to interpret experimental results that consider the duality wave-particle. This will allow us to apply the paraquantum logic analysis [16] - [18] to those studies.
We start by classifying two types of interference [15] [16] , as described below.
3.1.1. Type I Interference―Phenomenon with Two Waves in the Same Direction
We considered two waves traveling in the same direction and with the same frequency, same wavelength, same amplitude, but a lag. The first wave has phase constant equal to zero and the second wave has phase constant equal to φ [16] - [18] . For a particular wave case in which both are typified as progressive harmonic of sinusoid shaped, we obtain the respective wave equations:


where the wave number K is defined as 

The angular frequency is defined as


The relationship 

Therefore, interference is constructive if phase

3.1.2. Type II Interference―Phenomenon with Two Waves in Opposite Directions
If both waves have the same frequency, same wavelength and same amplitude, then for a particular wave case where both are progressive harmonics and sinusoid shaped, we have [12] - [18] :

The relationship 

The resulting wave equation originated from the interference phenomenon of interaction between two waves propagating in opposite directions, indicates that the resulting pulse is made of a static wave where each medium particle oscillates in Simple Harmonic Motion (SHM), with an amplitude whose magnitude depends solely on position, meaning, x [17] - [21] .
3.1.3. Two-Wave Region (2W Region) in Young’s Double Slit Experiment
When approaching the quantum phenomena with PQL, studies and analysis will be made considering the events that occur in a given area, located in the region between the two slits and the screen, as in Young’s experiment [9] [22] .
The reference point is located between the two slits, which is the origin of the reference line that cuts and separates the regions of interest between the two slits and the screen, given that the limits of final dimensions are set by Range of Interest, or Discourse Universe used in the analysis.
The wave interference phenomena that will be analyzed by the PQL occur beyond the two slits, called two-wave region (2W region).
In Figure 8 the 2W region, the focus of the analysis by the paraquantum logical model, is signaled in a representation of Young’s experiment.
3.1.4. Interference Phenomena in the 2W Region
Based on Figure 8, we can consider that when the wavefront pulse generated by a monochromatic light source is projected onto the two slits, they behave as two punctiform wave sources in relation to 2W region. Likewise, each slit presents a new pulse in which a wavefront propagates uniformly, inflationarily expanding within the 2W region.
Each pulse generated by monochromatic light source produces two identical twin pulses when it hits the slits, therefore indistinguishable and of identical physical properties. After the two slits, the identical twin pulses that were generated simultaneously will have their waves, or wavefronts, propagating as in an inflation process. During propagation, pulses interact with each other, as well as with wavefronts of remaining pulses within the 2W region.
The interaction between composed forces of wavefront particles in different pulses
Figure 8. Young experiment (double-slit) with emphasis on the propagating waves originated from the two slits in the 2W region.
generates Type I and Type II Interference phenomena. The closer the amplitudes of the two pulses in interaction, the greater the influence of Type II Interference. On the other hand, the greater the amplitude difference, the larger is the gap between interacting pulses, and as a consequence, the greater the effect of Type I Interference.
3.1.5. Generation of Oscillation Energy Pocket (Quantum) in the 2W Region
Figure 8 and Figure 9 show that Type II Interference occurs when two identical and indistinguishable twin pulses, generated by two slits, meet. This phenomenon results from the interaction of two waves propagating in opposite directions. Simultaneous generation places the meeting point of identical twin pulses of Type II Interference along the axis of the reference line located in the average distance between the two slits.
The addition the effect of Type II Interference to the inflationary effect in identical twin pulses results in oscillatory wave pulse propagation in 2W region.
The resulting wave pulse concentrates oscillatory energy and, as a consequence, behaves like an energy “pocket” or particle traveling, in a straight line, along the reference line axis. It is mathematically represented by the stationary wave in Equation (16). Using quantum mechanics nomenclature [2] [9] [23] - [27] , this pulse of concentrated energy moving along the 2W region is called Quantum.
Due to the effect of composing two types of interference phenomena, energy quanta (resulting from such composition) do not move in a straight line; instead, they move away from the reference axis as the lag increases. Details are shown in Figure 9.
Figure 9. Two types of interference occur in the 2W region resulting in inflationary behavior due to pulse propagation generated by double slit.
Figure 9 shows that for the largest phase difference, the effect of Type I interference is greater than that of Type II interference. This indicates that the smaller the phase difference between identical and indistinguishable twin pulses, the greater is the amount of wavefront and remaining pulses propagating in the 2W region. No phase difference indicates that the same wave is spreading in the 2W region.
4. Paraquantum Logical Model for Wave Theory
The application of PL in its special form that uses two annotation values (PAL2v) allows the determination of evidence Degrees extracted from measurements in the Observable in the real world [12] [13] .
Measured and Normalized values allow for the determination of the paraquantum logical state represented in its associated lattice (lattice of the PQL) that may be related to the Quantum. Therefore, paraquantum logical states are represented in the lattice of quanta’s paraquantum universe, or wave pulses of concentrated oscillation energy, that propagate in the 2W region of Young’s experiment.
4.1. Extraction of Evidence Degrees from the Interference Phenomenon in the 2W Region
In the Paraquantum Logical Model we will consider that the Observable is already represented in Type I and Type II Interference equations.
4.1.1. Evidence Degrees Extraction from Type I Interference
We can analyze the case in which function variations of evidence Degrees are always equal or above 0.5. The analysis will thus focus only on the upper right triangle of Lattice of the PQL (Quadrant I). Hence, Equation (15) is divided by 4, and then accrued by 1/2. Therefore, a favorable evidence Degree represented by the wave function when only Type I Interference occurs is obtained by Equation (17):

Comparing Equation (8) to Equation (17), we note that since two waves propagate in identical directions, this equation is valid only if the conflict degree is zero:
Equation (17) adapts perfectly to the Paraquantum Logical Model in cases where only Type I interference, which is related to two waves in the same direction, is studied.
Comparing the unit magnitude Ym to Equation (8), the certainty degree of its wave equation for a Contradiction Degree equals zero is calculated as follows:

For imposition

Figure 10 shows the division between the Paraquantum and physical universes, using the favorable evidence Degree in the upper right triangle of Lattice of the PQL (Quadrant I) with extraction of evidence Degrees from type I Interference.
Figure 10. Extraction of evidence degrees from Type I interference within the PQL Lattice (Quadrant I).
It is noted that for 
The Favorable evidence Degree obtained through Equation (17) is
The Unfavorable evidence Degree obtained through Equation (19) is
The Certainty Degree obtained through Equation (18) is
when:
The Favorable evidence Degree obtained through Equation (17) is
The Unfavorable evidence Degree obtained through Equation (19) is
The Certainty Degree obtained through Equation (18) is
For the wave equation with type I interference characteristics, where the function has
a lag angle of


indicates that this lag will only occur in Quadrant I of the Lattice of the PQL.
4.1.2. Evidence Degrees Extraction from Type II Interference
As before, the analysis is conducted in such way that the function variation always remains equal or above 0.5, so that the results will focus only on the upper right triangle of the lattice of the PQL [7] [12] (Quadrant I). For this to happen, Equation (16) is divided by 4 and then accrued by 0.5. Therefore, the favorable evidence Degree, represented by a wave function only for Type II Interference, is obtained by the equation:

In Type II Interference, quantum propagates only along the axis of the Contradiction Degree, with a certainty degree of zero. In this condition, comparing Equation (8) to Equation (17), we have:
Since we are studying only Type II Interference (two waves in opposite directions), Equation (20) perfectly adapts to the Paraquantum Logical Model. Thus, considering Equation (8) and the unit magnitude Ym, we define the Contradiction Degree for Type II Interference wave function as

For this condition, the unfavorable evidence degree is obtained by Equation (9), on the condition that the certainty degree is zero and the contradiction degree is given by Equation (21).

Figure 11 shows the split between the Paraquantum and the physical universes with a favorable evidence degree on the upper right triangle of the Lattice of the PQL (Quadrant I) with the extraction of evidence degrees from Type II Interference.
Imposing the condition
For
The favorable evidence degree obtained through Equation (19) is
The unfavorable evidence degree obtained through Equation (22) is
The contradiction degree obtained through Equation (21) is
when
The favorable evidence degree obtained through Equation (19) is
The unfavorable evidence degree obtained through Equation (22) is
The contradiction degree obtained through Equation (21) is
Figure 11. Extraction of evidence degrees from Type II interference within Lattice of the PQL (Quadrant I).
Therefore, for a wave equation with Type II Interference, where the function has a Kx value between


With such variation range of Kx, the Paraquantum Logical Model occurs only in Quadrant I of the Lattice of the PQL.
4.1.3. Extraction of Evidence Degrees from Type I and Type II Interference Phenomenon
In the composition of Type I and Type II Interference phenomena, there will be concentrated oscillation energy pulses. Quanta will thus exist traveling both along the 2W region beyond the reference line axis, as well as along non-rectilinear trajectories. This indicates that, under non-extreme conditions in the Paraquantum Logical Model, contradiction and certainty degrees coexist. By combining Equation (5) and Equation (6) with Equation (18) and Equation (20), we obtain equations of the two observables, which provide evidence degrees for Paraquantum analysis in the physical world. As a result, the two wave functions observed in the 2W region of the double-slit experiment will be mixed. Equation (17) must then be shown in its complete form that covers Type I and Type II Interferences, accounting now the contradiction degree:

The unfavorable evidence degree involving the two Quantum-wave equations propagating in the 2W region is

In Equation (23) and Equation (24), evidence degrees are determined by two wave functions characteristic of Quantum. In Paraquantum analysis, these two wave functions allow the representative values of the observable behavior to produce results that will be displayed in the Lattice of the PQL. Figure 12 shows the evidence degrees in the upper right triangle of the PQL (Quadrant I) where the two wave functions were extracted from the composition of Type I and Type II Interference in the 2W region.
4.2. Vector of State P(ψ) of Unitary Module Related to Two Wave Functions
Considering the two wave functions, the Vector of State of module P(ψ) represented in Equation (11) is calculated by:

Figure 12. Extraction of degrees of evidence from the composite Type I and Type II interferences within PQL Lattice (Quadrant I).
4.3. The Tangent of the Inclination Angle 
Equation (12), Equation (18) and Equation (21), calculate the tangent to the Vector of State P(ψ) inclination angle:
where, for:

Therefore, through Equation (21) we have:
By using the complement of the certainty degree, the phase difference angle of the two waves in the 2W region is

The contradiction degrees equated in Equation (21) can be expressed in the Lattice of the PQL solely by the inclination angle of Vector of State P(ψ), such that:

Therefore, under the condition of a Vector of State of unitary module, we can calculate, using the phase angle, the contradiction degree on the wave pulse of the concentrated oscillation energy that propagates through the 2W region.
In the two wave functions that characterize the Quanta in the 2W region, the certainty degree must be complemented. Therefore, Equation (23) and Equation (24) can be formulated as


The phase difference angle of the waves in Type I and Type II Interferences equals twice the inclination angle 

where: 

4.4. Superposed Paraquantum Logical States in the Paraquantum Logical Model
The trajectory of a wave pulse with concentrated oscillation energy, what we call Quantum, through the 2W region, where Type I and Type II Interferences phenomena occur, can be related to the vertex trajectory of Vector of State P(ψ) in the Lattice of the PQL. With some restrictions, the forecast of Paraquantum logical states (ψPQL) locations in PQL may correspond to the behavior of Quanta propagation in the 2W region.
Paraquantum logical states (ψPQL), represented by the Vector of State P(ψ) vertex of unitary module, are superimposed and their locations are related to Quantum characteristics through two wave functions shown in Equation (28) and Equation (29). Superposed Paraquantum logical states can be represented through Equation (10), such that:

where the Vector of State P(ψ) module must be a unit.
In Figure 13 we observe the vertex trajectory of Vector of State P(ψ) of unitary module, indicating superposed Paraquantum logical states (ψPQL).
Paraquantum Logical Model equations are defined in the upper triangle of Lattice of the PQL (Quadrant I). The analysis in these two Observables, whose values are added in equations of interference phenomena, will result in Paraquantum logical states (ψ) in the Lattice of the PQL located in Quadrant I. Their variations are defined in Equation (23) and Equation (24) and can be studied using Equation (28) and Equation (29). From the two intrinsic functions of wave equations, we can detect the effect of such measurements through the behavior of Logical states in Lattice of the PQL by representing the particles, or Quanta, that propagate in the 2W region.
4.5. Paraquantum Symmetry in PQL Model
The Paraquantum symmetry can be mathematically expressed by wave functions Equation (23) and Equation (24), regarded as evidence degrees, such that:
Figure 13. Trajectory of the Paraquantum logical states and values involved in the upper-right corner of the PQL Triangle Lattice.
a) Given the equation for the favorable evidence degree in Quadrant I of the Lattice of the PQL;
the certainty degree can be isolated such that:

Comparing Equation (5) to (32), we have for Quadrant I:



The Paraquantum logical state will be 


Therefore, a Paraquantum logical state with positive certainty degree indicates that the latter is within quadrant I of the Lattice of the PQL.
b) Given the equation of the unfavorable evidence degree in Quadrant I of the Lattice of the PQL;

the certainty degree can be isolated, such that:

Comparing Equation (5) to Equation (33), we have for Quadrant I:



The Paraquantum logical state is 

In this case, the favorable evidence degree (µ(x,t)) was exchanged by the unfavorable evidence degree (λ(x,t)) which sets a logical negation operation in PQL, as defined by Equation (7).
The Paraquantum logical state with a negative certainty degree obtained in analysis b indicates that it is located within Quadrant II of the Lattice of the PQL, which configures a symmetry (mirror) Paraquantum logical state in the model.
This analysis indicates how the entanglement of several concentrated energy pockets, or quanta, is modeled by PQL in the 2W region in the double slit experiment. When a logical state of two-wave functions is created, a mirror logical state occurs, thus creating an intertwine of models by evidence degrees represented in the two wave functions.
4.6. Complete Paraquantum Logical Model Represented in One Spatial Dimension
When studying the Quantum, the Paraquantum Logical Model is considered complete in a one spatial dimension when the quantum interference phenomenon is represented in all four quadrants of the PQL.
As seen in the previous figure, Vector of State P(ψ), represented by its inclination angle αψ ranging from 0 to π/4 according to the variation of two wave functions, was restricted to Quadrant I (upper triangle located to the right of PQL). However, the analysis can be done in one spatial dimension, but in a reference line that bisects the 2W region and creates another Vector of State P(ψ)II, of unitary module, whose origin in PQL coincides with the False Paraquantum logical state vertex. This Vector of State is formed in Quadrant II (upper triangle to the left of PQL).
For the complete model, we consider a particle, or Quantum, with inflationary expansion to be represented in four directions (up, down, right, left) of a geometric plane. Thus, in PQL, for each Vector of State P(ψ)I created in the upper right triangle, there will be another Vector of State P(ψ)IV formed in the lower right triangle. Likewise, for each Vector of State P(ψ)II created in the upper left triangle, there will be another Vector of State P(ψ)III formed in the lower left triangle.
To obtain the values corresponding to these mirror Vector of States P(ψ) (located in the lower triangles), an operator must be created to multiply the contradiction degree by −1. Therefore, this representation of a Paraquantum state in PQL can be described using Dirac’s bra-ket notation [23] , in which while creating a Ket, the Vector of State P(ψ)I in Quadrant I imposes the creation of its vertex bra, Vector of State P(ψ)IV, through a Paraquantum Logical Operator. Figure 14 shows the Paraquantum Logical Model of concentrated oscillation energy pulse wave, called Quantum, with the Vector of States and representations of their two wave functions.
4.7. PQL Lattice Representation in the Set of Complex Numbers
Complex numbers have infinite applications and may, in many cases, facilitate calculations and shorten notations. To adapt PQL concepts to quantum mechanics, it is possible to use complex numbers to represent values in Lattice of the PQL. This work only summarizes the key properties necessary for one spatial dimension Paraquantum Logical Models.
A complex number is expressed as

Number 

Following the Paraquantum Logical Model, in the representation of complex numbers via PQL Lattice, the real part z is related to the certainty degree (DC), and the imaginary part is related to the contradiction degree (Dct). Therefore, complex number expressions such as 

Given two Paraquantum complex numbers


Figure 14. Paraquantum Logical Model of Oscillation energy pulse-quantum relations between the PQL Lattice triangles and the 2W regions locations represented in 4 directions on the geometric plane.
the sum is given by
with the restriction that the values stay within the Lattice.
The product of z1 and z2 is given by:
If 



The norm of Z is 

The norm of a Paraquantum complex number is
The norm of a complex number is always a non-negative real number.
Complex numbers can be geometrically represented using a Cartesian plane.
The complex number 

In the geometric representation of complex numbers, we obtain the polar representation:
The Paraquantum complex numbers can thus be represented only by:
Representing the lattice of the PQL by a set of complex numbers, contradiction degrees, which are arranged along the vertical axis, are represented by imaginary numbers (i); and degrees of certainty, which are arranged along the horizontal axis, are represented by real numbers. The function of superposed Paraquantum logical states is represented in Equation (31) can be described as

The Paraquantum logical state represented in Equation (10) is now represented by a complex number:

Through Equation (7) we obtain the logic negation of the Paraquantum logical state, such that:

Similarly, for the Paraquantum logical state 

the PQL for a set of complex numbers, we can find ψPQ4, using a complex conjugate operator, which is its symmetrical in ψPQ1 in relation to the contradiction degree.
The amplitude of Vector of States P(ψ)I and P(ψ)I components are represented by the contradiction degree in both the imaginary vertical axis 

The set of complex numbers of Vector of State P(ψ)I in Quadrant I, is represented by its horizontal component 


with: 
By similar reasoning, the representation in the set of complex numbers of Vector of State P(ψ)IV in Quadrant IV is given by its complex conjugate; thus by its horizontal component 


where:
4.8. Vector Representation in the PQL Lattice in a Set of Complex Numbers
Using the set of complex numbers applied in the Lattice of the PQL, we can obtain a complete Quantum model with a one spatial dimension representation. Thus, we use the Bra-ket notation, or Dirac’s notation [24] to represent Vector of State―the closest nomenclature in quantum mechanics [2] [3] .
4.8.1. The Bra-ket Notation
In quantum mechanics, the physical state of a system is identified as a unitary radius in a separable Hilbert space complex H, or equivalently, by a point in Hilbert’s space projected by a system. Each vector within the radius is called a “ket” and represented


Using Dirac’s notation [24] in the fundamentals of PQL, we consider in the first quadrant:
which is the vector
Normalized values corresponding to this Vector of State P(ψ)I for an inclination angle 
Evidence degrees: 
Paraquantum logical state:
Complex Paraquantum logical state:
Vector Ket 


Normalized values corresponding to a Vector of State P(ψ)IV for inclination angle 
Evidence degrees: 
Paraquantum logical state:
Complex Paraquantum logical state:
Vector Bra 


Normalized values corresponding to this Vector of State P(ψ)II, for inclination angle 

Paraquantum logical state:
Complex Paraquantum logical state:
Vector ⌐Ket 


Normalized values corresponding to this Vector of State P(ψ)III, for inclination angle 
Evidence degrees: 
Paraquantum logical state:
Complex Paraquantum logical state:
The vector ⌐Bra 
Figure 15 shows the representation of the Lattice of the PQL, with Paraquantum logical states defined by complex numbers. The same graph shows the amplitude variation of wave functions as well as lag angles resulting from inclination variations αψ of four Vector of States.
A complete model of a Quantum is represented in one dimensional space, where correlations are conducted between variations of the two representative wave functions of the Quantum in the 2W region and the corresponding variation of lag angle ϕ and inclination angle αψ of Vector of States.
With this correlation we can determine numerical values in the Lattice of the PQL, which enables to identify logical states and to draw analogies with energy levels and probabilities regarding particles location in the 2W region. Figure 15 shows that for the point where wave functions meet, the lag angle is zero (ϕ = 0) and the vectors with inclination angle αψ = 0 have all their vertices on the point equidistant from the four corners of the Lattice of the PQL, what is considered an Undefined Logical state (I).
A vectors exchange then takes place―vector Ket becomes a Bra vector; the latter in turn, becomes a Ket. The same behavior applies to vectors under logic negation. This change, however, refers to an observation from Quadrant I, but what occurs is a transition which establishes that both vectors (Ket and Bra), suffer a 90˚ variation in their inclination angle.
4.8.2. The Paraquantum Correlation
Paraquantum interlace is represented through the two wave functions that generate the Logical State of each State vector, therefore also the superposed logical States that appear in its vertices. As can be seen in Figure 15, each State vector in the quadrants
Figure 15. Representation of Vector of States in the PQL Lattice; and variations of evidence degrees characteristic of the two Quantum- wave functions.
of the PQL Lattice presents in its vertex the Logical State that is the result of the paraquantum correlation between two wave functions. Representing the symbol ◊ as paraquantum correlation we have to:
The logical State 


The logical State 


The logical State 


The logical State 


We can see that at equilibrium:
a) For the vectors 


b) For the vectors 


The symmetry between the four Vectors of States at equilibrium results in equality of wave functions:
In this way, all the functions of the waves Energy package are in paraquantum interlace and maintains the equilibrium of the four State vectors in the Lattice of LPQ.
The collapse of the wave functions happens when there is a disturbance in the equilibrium of the system and thus leads to destruction of vectors. This imbalance causes the cancellation of the degree of contradiction and results in the logical State in two related vertex points t (true) and F (false) the Lattice of LPQ. The symmetry and entanglement are not maintained and the occurrence of the collapse of the Wavefunction.
For condition true (t):




For condition false (F):




4.9. Frequency f of Wave Functions in Paraquantum Analysis
In a physical medium, the increase in frequency f on wave functions implies a decrease in lag angle ϕ and, consequently, the maximum inclination angle αψmax of Vector of States will be smaller than the fundamental, as shown in Figure 15. This increased frequency in wave functions causes the Vector of States to vibrate closer to the equidistant point between the Lattice of the PQL vertices, where we find the Undefined Logical state (I).
This means that the smaller the slope angle αψmax―the closer the vertex of Vector of State P(ψ) is to the Undefined Logical state I represented by PQL―the greater energy E; however, the lower will be its definition represented by a lower certainty degree (DC). In Equation (15) and Equation (16), which express Type I and Type II Interference phenomena, it is possible to observe that while frequency f increases, wavelength λ decreases, wave number K increases, period T reduces, and angular frequency w increases [25] [26] . In terms of PQL concepts, this means that in the Paraquantum Logical Model, Quantum Energy E is related to the increased intensity of the contradiction degree and to the uncertainty of its route or location; its Momentum thus relates to the intensity of the certainty degree. Therefore, energy can be related to the contradiction degree, such that:

And a relation between momentum and certainty degree, such that:

The two previous equations are confirmed by the fact that, due to characteristics of the two wave functions that form the concentrated oscillation energy pulse (quantum), vibrations of the Vector of State P(ψ) around an Undefined I logical state can happen only with certain maximum inclination angles αψmax. This gives intensities contradiction and certainty degrees their discrete characters, respectively related to its energy E and Momentum M.
Evidence degrees represented by the two wave functions in the physical medium (2W region) have values reduced by a fraction determined by wavelength λ, therefore from wave frequencies within the envelope, which in turn, is considered fundamental and has its own wavelength λF. After the fundamental frequency―of evidence degree equal to a unit (μ = 1.0) and the maximum inclination angle αψmax = π/4―the only possible frequency f of an internal wave will be the one with an evidence degree of µ = 0.75. Similarly, the only possible following frequency will be the one with a evidence degree of µ = 0.625. This evidence degree decreases as the internal wave frequency increases within the fundamental frequency’s envelope. Figure 16 depicts this condition in which signals having higher frequencies and higher energy produce smaller evidence degrees when introduced into a concentrated oscillation energy pulse.
Figure 16. Representation of the two wave functions in the physical environment, where higher frequency signals produce smaller evidence degrees determined by wavelengths.
4.10. Energy (E) and Momentum (M) in the Lattice of the PQL
As seen in Figure 16, given a certain wave length λ in the Paraquantum Logical Model, the next possible larger wave length within the concentrated oscillation energy envelope may only be twice the value of λf. Similarly, the next possible lower wavelength can only be half of λf.
For increased frequency f, with a unit favorable evidence degree and its next maximum value of μ = 0.75, we can calculate through Equation (23) the certainty degree (DC) given a contradiction degree Dct = 0:
In the Lattice of the PQL, the diagonal angle 
diction degrees at Dct = 0.5. The line equation is
gree function is given by:

The intensity of the contradiction degree that relates to energy is found through the Lattice of the PQL analysis, as shown in Figure 17.
The relation between a circumference equation 


As seen in Figure 17, by intersecting the straight line Equation (41) with the circle Equation (42), we obtain the coordinates of the point where the new maximum Para- quantum logical state ψ(max2) is located in the Lattice of the PQL, for this frequency. We thus have Dct = 0.089820278.
Inputting this value into Equation (42), we find:

For the wave function in the physical environment, shown in the Lattice of the PQL, the favorable evidence degree is now calculated by Equation (28):
Figure 17. Representation of Energy standardized in the Lattice of the PQL, related to intensity of the contradiction degree.
which reflects the expected value. Likewise, an unfavorable degree evidence is now calculated by Equation (29):
Normalized energy value is calculated by Equation (39):
Normalized Momentum value is calculated by Equation (40):
The Paraquantum logical state, in the vertex of the Vector of State for the maximum inclination angle, is represented by Equation (10), which in Quadrant I is given by:

Represented through a set of complex numbers
Represented in the Lattice of the PQL by the Vector of State unit module
The same procedure is used to determine the remaining three quadrants.
4.11. Quantum Leap in the Lattice of the PQL
We can further conduct an analogy between the intensity of the contradiction degree (Dct)―a standard value in the imaginary axis of the Lattice of the PQL―and the Quan-
tum energy. The value shifted from 


ues found in the equations.
For further increase in frequency, given the previous favorable evidence degree of μ = 0.75, its next possible maximum value must be μ = 0.625. Calculating the favorable evidence degree through Equation (27), with a contradiction degree Dct = 0, we have:
From where the certainty degree is obtained:
The straight line equation is then:

By intersecting the straight line Equation (43) with the circle equation Equation (42) we obtain the point coordinates for the new maximum Paraquantum logical state (ψmax3) at this frequency. Thus:
Inputting this value in Equation (43) gives

Figure 18. Paraquantum Logical Model of the Quantum for an initial frequency below the fundamental.
reflects the expected value.
Likewise, the unfavorable evidence degree is now calculated by Equation (29):
Normalized energy value is calculated by Equation (39):
Normalized Momentum value is calculated by Equation (40):
The Paraquantum logical state at the vertex of the Vector of State for the maximum inclination angle is represented by Equation (10), which in Quadrant I is



The same procedures apply to the remaining three quadrants of the Paraquantum Logical Model.
Similarly, drawing an analogy between the intensity of contradiction degree (Dct)―a standard value along the Lattice of the PQL imaginary axis―and the Quantum energy, this value increases from 


This condition is shown in Figure 19, where the equation values are verified.
The intensity of the contradiction degree (Dct) and its Normalized value compared to Quantum energy can be studied in comparison to analysis conducted using Schrödinger’s equation. Such procedures will be discussed in Part II of this work.
5. Conclusion
This first part presents a model based on Paraquantum Logic (PQL) where concentrated oscillation energy particle, an energy Quantum, can be represented by two wave functions. Under this approach, the Quantum was able to be represented both in the physical world―through quantum phenomena observed and governed by two wave functions―as well as in the Paraquantum universe represented by a Lattice of the PQL―where wave theory concepts can be better understood. We hereby present a complete Quantum model in a geometric plan where we identified logical states and Vector of States similar to those studied by quantum mechanics theory and broached by Dirac. The Paraquantum Logical Model presented here has advantages, shown mostly in its logic reversibility properties, a premise for conducting studies on particle-wave theory in two universes, Paraquantum and physical. The PQL Model where they operate four State Vectors (Ket, Bra, ⌐Ket, ⌐Bra) with symmetrical features and entanglement, is quite interesting for the subsequent studies related to quantum computing. This premise is important to the study of quantum phenomena that allows calculation and observation of the effects as states and energy levels encompassing all the terms in Schrödinger’s equation and expanding to probabilistic analysis. These procedures will be studied in Part II of this work.
Figure 19. Quantum’s Paraquantum Logical Model, for a second frequency below the fundamental.
Acknowledgements
We thank Newton C. A. Da Costa (PhD) who was one of the creators of Paraconsistent Logic.
We thank Crimson Interactive Pvt. Ltd. (Ulatus)―www.ulatus.com.br for their assistance in manuscript translation.
Cite this paper
Da Silva Filho, J.I. (2016) Undulatory Theory with Paraconsis- tent Logic (Part I): Quantum Logical Model with Two Wave Functions. Journal of Quantum Information Science, 6, 143-180. http://dx.doi.org/10.4236/jqis.2016.63012
References
- 1. Faraday, M. (1831) On the Forms and States of Uids on Vibrating Elastic Surfaces. Philosophical Transactions of the Royal Society London, 52, 299-340.
http://dx.doi.org/10.1098/rstl.1831.0018 - 2. Barr, E.S. (1963) Men and Milestones in Optics II. Thomas Young. Applied Optics, 2, 639-647.
http://dx.doi.org/10.1364/AO.2.000639 - 3. Griffiths, D. (1995) Introduction to Quantum Mechanics. Prentice Hall, Upper Saddle River, New Jersey.
- 4. Sakurai, J.J. (1994) Modern Quantum Mechanics. Revised Edition, Addison-Wesley Publishing Company, Reading, MA.
- 5. Da Costa, N.C.A. (1974) On the Theory of Inconsistent Formal Systems Notre Dame. Journal of Formal Logic, 15, 497-510.
http://dx.doi.org/10.1305/ndjfl/1093891487 - 6. Blair, A.H. and Subrahmanian, V.S. (1987) Paraconsistent Logic Programming. 7th Conference on Foundations of Software Technology and Theoretical Computer Science, Pune, 17-19 December 1987, 340-360.
http://dx.doi.org/10.1007/3-540-18625-5_59 - 7. Da Costa, N.C.A., Subrahmanian, V.S. and Vago, C. (1991) The Paraconsistent Logic PJ. Mathematical Logic Quarterly, 37, 139-148.
http://dx.doi.org/10.1002/malq.19910370903 - 8. Da Silva Fiho, J.I., Lambert-Torres, G. and Abe, J.M. (2010) Uncertainty Treatment Using Paraconsistent Logic: Introducing Paraconsistent Artificial Neural Networks. IOS Press, Amsterdam, 328.
- 9. Qureshi, T. (2012) Modified Two-Slit Experiments and Complementarity. Journal of Quantum Information Science, 2, 35-40.
http://dx.doi.org/10.4236/jqis.2012.22007 - 10. Da Silva Filho, J.I. (2011) Algorithms Based on Paraconsistent Annotated Logic for Applications in Expert Systems. In: Segura, J.M. and Reiter A.C., Eds., Expert System Software: Engineering, Advantages and Applications, Nova Science Publishers, Hauppauge, 1-40.
- 11. Da Silva Filho, J.I. (2014) An Introduction to Paraconsistent Integral Differential Calculus: With Application Examples. Applied Mathematics, 5, 949-962.
http://dx.doi.org/10.4236/am.2014.56090 - 12. Da Silva Filho, J.I. (2011) Paraconsistent Annotated Logic in Analysis of Physical Systems: Introducing the Paraquantum Factor of Quantization hψ. Journal of Modern Physics, 2, 1397-1409.
http://dx.doi.org/10.4236/jmp.2011.211172 - 13. Da Silva Filho, J.I. (2011) Analysis of Physical Systems with Paraconsistent Annotated Logic: Introducing the Paraquantum Gamma Factor γψ. Journal of Modern Physics, 2, 1455-1469.
http://dx.doi.org/10.4236/jmp.2011.212180 - 14. Da Silva Filho, J.I. (2012) Analysis of the Spectral Line Emissions of the Hydrogen Atom
with Paraquantum. Journal of Modern Physics, 3, 233-254.
http://dx.doi.org/10.4236/jmp.2012.33033 - 15. Da Silva Filho, J.I. (2012) An Introductory Study of the Hydrogen Atom with Paraquantum Logic. Journal of Modern Physics, 3, 312-333.
http://dx.doi.org/10.4236/jmp.2012.34044 - 16. Tipler, P.A. and Llewellyn, R.A. (2007) A Modern Physics. 5th Edition, W. H. Freeman and Company, New York.
- 17. Mckelvey, J.P. and Grotch, H. (1978) Physics for Science and Engineering. Harper and Row, Publisher, Inc., New York, London, 426 p.
- 18. Peres, A. (1993) Quantum Theory: Concepts and Method. Kluwer Academic Publishers, Dordrecht, The Netherland.
- 19. Tipler, P.A. and Tosca, G.M. (2007) Physics for Scientists. 6th Edition, W. H. Freeman and Company, New York.
- 20. Ference Jr., M., Lemon, H.B. and Stephenson, R.J. (1956) Analytical Experimental Physics 2nd Edition, University of Chicago Press, Chicago, USA.
- 21. Bernstein, J., Fishbane, P.M. and Gasiorowicz, S.G. (2000) Modern Physics. Prentice-Hall, Upper Saddle River, New Jersey, 624 p.
- 22. Feynman, R.P., Leighton, R.B. and Sands, M. (1965) The Feynman Lectures on Physics. Addison-Wesley, Reading, Massachusetts-London.
- 23. SchrÖdinger, E. (1926) An Undulatory Theory of the Mechanics of Atoms and Molecules. The Physical Review, 28, 1049-1070.
http://dx.doi.org/10.1103/PhysRev.28.1049 - 24. Dirac, P.A.M. (1958) The Principles of Quantum Mechanics. 4th Edition, Oxford University Press, Oxford, UK.
- 25. Narasimhachar, V., Poostindouz, A. and Gour, G. (2016) Uncertainty, Joint Uncertainty, and the Quantum Uncertainty Principle. New Journal of Physics, 18, Article ID: 033019.
http://dx.doi.org/10.1088/1367-2630/18/3/033019 - 26. Dammeier, L., Schwonnek, R. and Werner, R.F. (2015) Uncertainty Relations for Angular Momentum. New Journal of Physics, 17, Article ID: 093046.
http://dx.doi.org/10.1088/1367-2630/17/9/093046 - 27. Zhang, W.R. (2016) G-CPT Symmetry of Quantum Emergence and Submergence—An Information Conservational Multiagent Cellular Automata Unification of CPT Symmetry and CP Violation for Equilibrium-Based Many-World Causal Analysis of Quantum Coherence and Decoherence. Journal of Quantum Information Science, 6, 62-97.
http://dx.doi.org/10.4236/jqis.2016.62008




















































































































