Received 15 April 2015; accepted 30 August 2015; published 2 September 2015

ABSTRACT

This report describes an approach for representation of quantum operators through rotations and rotation through quantum operators. The approach of the proposed method transforms rotation in a kind of a unitary matrix that corresponds to the rotation. Operations with qubits are very similar to the rotation, but with an added phase coefficient. This fact is used to create a process for rotation between unitary matrices. This approach could be used to modifying the controls to apply in a different basis.

Keywords:

Quantum Operators, Rotations, Phase Space, Quantum Circuit

1. Introduction

The fundamental concept for realization of the transitions is based on the fact that the quantum operation is always just a unitary matrix, which may be a linear interpolation between the matrices: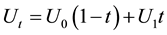. The operations with single qubits are very similar to the rotations, but with an added coefficient of the phase. This fact will be used to create a method for transformation of rotational into qubit operations.

Rotations of the eigenvector of qubit could be viewed as operations in a single Bloch sphere [1] -[3] . A more formal approach is to provide two or three fixed orthogonal axes of rotation. This allows arbitrary rotations in three or less steps, for example, by using the angle of the construction of Euler. Logical qubits, composed of two or more physicalturns, are possible physically different binding mechanisms to control different axes of rotation of the field unit. For example, logical qubits formed in double quantum dots use local gradients for generating rotations around an axis, and switched interactions generate rotations around an orthogonal axis [4] [5] . In this paper, cases of intermediate situations between these two extremes are investigated, where rotations can be performed around an arbitrary axis constrained to lie in one plane. The main motivation for our work is the example of single exchange of logical Qubit in triple quantum dot [6] [7] . We will build on the known results [8] that the internal connections between the physical spins in one exchange-only qubit can be used to generate a consistent set of rotations in the XZ basis of qubit [9] .

In the development process of a circuit, quantum simulator [10] - [15] was required to seek solutions to approximate the results of the quantum operations, in order to animate what occurs without any sharp jumps. More generally, a transition was necessary between the two operations without any jumps. This paper will show that such rotations in a single plane reduce the total number of steps required for Qubit operations. For example, a transformation of a state that converts specific baseline to a certain final state can be carried out in one stage, random rotation single-Qubit can be done in two stages. We offer constructive solutions to these problems. Given that the space of the unit matrix is very similar to the space of rotations, it is useful to turn into a kind of rotation of the unit matrix which corresponds to the rotation in some useful way. The simplest method of achieving this is to provide such a rotation as a quaternion, and then replace the quaternion components with the relevant times of Pauli matrices:

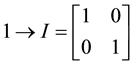
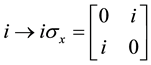
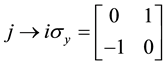
If the input rotation is a vector v, where the direction of v is the axis of rotation and the length 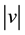is the number of rotations in radians, then the unitary matrix will turn this rotation in:

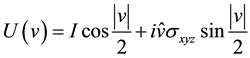
where 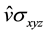gives the vector of Pauli in v.

The problem with the linear transformation is that the intermediate matrices may not be valid operations. The linear transformation tends to create a matrix entries, which are too close to zero, i.e. the resulting matrices will shrink the values instead of retaining their length (which is not a desired effect, as the whole point of using unitary matrices is to preserve the length). Actually, the goal is to be made a transformation without leaving the space of the unitary matrices. A compact way for the parameterization of the space of the unitary matrices is:

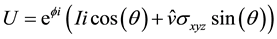
The above equation includes four constants and three variables. The constants are the identity matrix (I), the square root of −1 (i), the constant of Euler (e) and the vector of Pauli matrices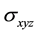. The three variables are the angle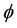, the angle 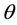and the single vector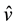. Each of the variables plays a different role. 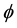is a global phase coefficient. It’s what distinguishes the group of unitary matrices U(2) from “the special unitary group SU(2)”. 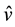and 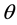correspond to a rotation. is like an axis to rotate around, and is how much to rotate around the said axis. What does it mean that and are like a rotation? It becomes a bit clearer when the compact parameterization from above is expanded. Through incorporation of the Pauli matrices and splitting of in, the following is obtained:

This is not yet clear enough. The following part is omitted: the equation to convert from an axis-angle style rotation to a single quaternion style rotation:

The resemblance is visible. Without paying attention to the mysterious division by 2 of the angles, the Pauli matrices actually play the role of quaternion constants: i, j and k. If each of the Pauli matrices is multiplied by i, the following is obtained:

This, in turn, looks very similar to the way in which the quaternions are defined:. Why is this similarity with the rotations important? Because it will be used for linear transformation. There are already existing methods for smooth linear transformation between quaternions and they will be applied in order to be handle the rotation part of the unitary operation. Then the remaining phase part simply must be inter- polated between two angles.

The main contribution of this paper is the proposed method of mapping rotations in unitary matrices.

2. Converting Rotation into Qubit Operations

The general comparison has got many good features, but also two flaws that, if possible, should be avoided. The first flaw is that the angles are divided by 2. Therefore, a rotation of 360˚ does not return to the starting position, but to. If we use this mapping, the rotation should be of 720˚, which is confusing. The second flaw is that there is no rotation, which corresponds to Pauli matrices. Rotation of 180˚ around the X axis gives instead of. This means that when using these rotations to define operations for quantum computer, a NOT exit cannot be even made! It is possible these flaws to be avoided, but this will be at the expense of something else.

2.1. Phase Correction

Both of the aforementioned flaws are caused by one problem: the global phase coefficient is wrong. In order to fix it, we have to add a specially prepared coefficient of the counter-phase. Currently a half-turn around the X axis gives. To turn it into, a phase correction factor of will be needed. Similarly, a coefficient with phase correction of −1 for one full turn is also needed. After three half rotations around the X axis (or one half turn around the negative X axis) a coefficient with phase correction of i is needed. The coefficients with phase correction are the same for the Y and Z axes with respect to the amount of turning. Given the above in-

formation, it’s clear that is needed a correction coefficient such as, where s is either +1, or −1, depending

on the direction of rotation. Choosing s is a delicate moment, which will be discussed later. For now, it will be used in the mapping as taken for granted:

Because the mapping formula already has two coefficients involving half-angles being multiplied together, there are possibilities for their simplification. Let us first reveal in the trigonometric functions:

Then it will be divided, while the trigonometric multiplications are simple, but the elements are not yet grouped based on the matrix coefficients:

Let’s make the trigonometric coefficients more similar by subtracting the sign coefficients in relation to the parity (i.e. and):

Double-Angle formulas expressing trigonometric functions of an angle 2x in terms of functions of an angle x,

Simplification of the coefficients:

Subtraction of from the component on the right side:

The coefficient of s is moved into the trigonometric functions, so they can be merged in the exponential functions:

This is already simple enough. The fact that the angles are no longer being divided by two 2, shows, that the problem with 720˚ is solved. Evaluating the mapping at, and does not give back, , and respectively. These are the correct results, with the exception of the detail that should be canceled in the results by selecting s in an appropriate manner.

How should be selected whether s must be +1 or −1? A naive solution would be to always use s = 1 or −1, but

that would cause (for example) to differ from despite starting from equivalent

rotations. Negating a vector has to negate s, because, otherwise, repeatedly doing and undoing a rotation would give matrices that were not inverses of each other. This in turn will cause an increase in the phase coefficient instead of its change together with the rotations. The reversal of s without introducing a discontinuity in the phase correction requires to be an integer from half of the turns, as this is the only time when. However, s must be reversed for all pairs, including those, which are not half rotations, and the axis, can be rotated so as to correspond to reversals. Thus, regardless of the actions, there always will be a discontinuity in the phase correction angle (Figure 1).

The plane, in which the discontinuity occurs, can be rotated so that no rotational axes are used on it. Note that, even if you avoid rotation axes along the bad plane, you will still run into problems when combining multiple rotations. This is a consequence of wanting half turns to correspond to the Pauli matrices. There's no way to avoid accumulating a global phase factor via multiple rotations because, although rotating a half turn around the X then Y then Z axis does not give a final rotation, and. In the end, despite the elimination of the two flaws from the original mapping (the rotation at 720˚ and the inability to obtain the Pauli matrices) now there is a discontinuity, where the sign of the result is switched when the rotational axis is swiveled, and there is a problem with the phase accumulation at multiple rotations. Whether or not these disadvantages are preferable over the initial ones depends on the particular application.

2.2. Implementation

Here is python code implementing the final mapping from above:

# Warning: with disadvantage; see below

defq_rotation_to_matrix(x=0, y=0, z=0):

# Discontinuance of the phase correction in an inconvenient plane

s = math.copysign(1, −11*x + −13*y + −17*z)

theta = math.sqrt(x**2 + y**2 + z**2)

v = x * np.mat([[0, 1], [1, 0]]) +y * np.mat([[0, −1j], [1j, 0]]) + z * np.mat([[1, 0], [0, −1]])

ci = 1 + cmath.exp(1j * s * theta)

# Potential division by zero!

cv = s * (1 − cmath.exp(1j * s * theta))/theta

return (np.identity(2) * ci − v * cv)/2

A notable problem in the above code is the division of the rotation angle in order to compute the unit vector

along the axis of rotation. This will cause problems at small rotations. Thus, the part must be rewritten so it does not involve a division. To avoid the division can be used the sine function. Let’s

first reveal the exponential functions into trigonometric, then they should be simplified and the half-angle identities should be used and they should be simplified again:

Although the sine also has a division by zero, it can be used the fact that acts as x near zero in order to

eliminate the problem. Upon approaching to zero, the series, divided by x, gives a good enough approximation. If we switch from direct computing of to using the approximation around the time where starts being rounded to 1. Given the stable sine function, and

the arbitrarily chosen plane-of-terribleness we can write the function rotation_to_matrix: defquantum_ rotation_to_matrix (x=0, y=0, z=0):

It returns a unitary matrix that corresponds, in a useful, but not unique way, to a rotation around the axis by sqrt(x^2 + y^2 + z^2) radians.

# Discontinuance of the phase correction in an inconvenient plane

s = math.copysign(1, −11*x + −13*y + −17*z)

theta = math.sqrt(x**2 + y**2 + z**2)

v = x * np.mat([[0, 1], [1, 0]]) +y * np.mat([[0, −1j], [1j, 0]]) +z * np.mat([[1, 0], [0, −1]])

ci = 1 + cmath.exp(1j * s * theta)

cv = math.sin(theta/2) * sinc(theta/2) - 1j * s * sinc(theta)

return (np.identity(2) * ci - s * v * cv)/2

defsinc(x):

It returns sin(x)/x, but computed in a way that does not explode when x is equal to or near zero.

sinc (0) is 1.

sinc(0) is 1.

if abs(x) < 0.0002:

return 1 − x**2/6

return math.sin(x)/x

It could be double-checked, whether the function is working correctly by printing out a few test values:

np. q_setup_printoptions(precision=5, suppress=True)

print "I", q_rotation_to_matrix()

print "I_2", q_rotation_to_matrix(x=2*math.pi)

print "X", q_rotation_to_matrix(x=math.pi)

print "Y", q_rotation_to_matrix(y=math.pi)

print "Z", q_rotation_to_matrix(z=math.pi)

print "H", q_rotation_to_matrix(x=math.pi / math.sqrt(2), z = math.pi / math.sqrt(2))

print "sqrt_1(X)", q_rotation_to_matrix(x=math.pi/2)

print "sqrt_2(X)", q_rotation_to_matrix(x=−math.pi/2)

Which prints out:

I [[ 1.+0.j 0.+0.j]

[ 0.+0.j 1.+0.j]]

I_2 [[ 1.+0.j 0.−0.j]

[ 0.−0.j 1.+0.j]]

X [[ 0.−0.j 1.+0.j]

[ 1.+0.j 0.−0.j]]

Y [[ 0.−0.j 0.−1.j]

[−0.+1.j 0.−0.j]]

Z [[ 1.+0.j 0.+0.j]

[ 0.+0.j −1.−0.j]]

H [[ 0.70711−0.j 0.70711+0.j]

[ 0.70711+0.j −0.70711−0.j]]

sqrt_1(X) [[ 0.5−0.5j 0.5+0.5j]

[ 0.5+0.5j 0.5−0.5j]]

sqrt_2(X) [[ 0.5+0.5j 0.5−0.5j]

[ 0.5−0.5j 0.5+0.5j]]

Those values look good to me (modulo the rounding error introduced by the involvement of π and). The half-turns along each axis give the corresponding Pauli matrix, rotating one full turn gets us back to the identity matrix, the quarter turns are square roots of the half turns. The Hadamard matrix is obtained by rotating a half turn around the X + Z axis.

3. Converting the Transitions between Quantum Gates in Rotary Operations

First the unitary operation must be broken down into its quaternion and phased parts. Let’s start by braking down the previous parameterization of the unitary group into a single matrix:

The values for extraction are the phase f and the quaternion components It must be observed that and contribute only for the upper right and lower left part of the matrix. In addition, contributes symmetrically, while - asymmetrically. This allows to be solved their values, although they are still mixed with the phase, by taking the sum and the difference along the diagonal. The same applies for and along the other diagonal. To eliminate the coefficient from the extracted values, is used the fact that it should be the only contributor of the complex values. Any component from the extracted four quaternion components can be selected (as long as it's not zero) and pick a phase coefficient, which will make the chosen component real. Since the given matrix certainly is unitary, the same coefficient of the phase should make the remaining quaternion components real. Below is given a code, written in python, which carries out the described factorization:

defquantum_unitary_breakdown(m):

Breaks an unitary matrix in quaternion and phase components.

# Extract rotation components

a, b, c, d = m[0, 0], m[0, 1], m[1, 0], m[1, 1]

t = (a + d)/2j

x = (b + c)/2

y = (b − c)/−2j

z = (a − d)/2

# Extracts common phase coefficient

p = max([t, x, y, z], key=lambda is: abs(e))

p /= abs(p)

pt, px, py, pz = t/p, x/p, y/p, z/p

q = [pt.real, px.real, py.real, pz.real]

return q, p

After the problem can be broken down into factors in the rotation and phase parts, and they can be inter- polated separately. For the rotation part will be used a spherical transformation. In order to be interpolated spherically between two points―and must be found an angle, satisfying, and then the result is:

The obstacle here is the division by zero, when is zero. Fortunately, because the numerator is approaching zero generally in the same way as the denominator, this is a case in which the obtained value does not deviate. A

function can be defined, which calculates, but switches to an approximation, that does not divide by

zero or increase the errors at floating point numbers, when they are close to zero:

defquantum_sin_scale_ratio(theta, factor):

Returns sin(theta * factor) / sin(theta) with care around the origin to avoid dividing by zero.

# Near zero, transition to an approximation, to avoid an increase from error at floating point numbers.

if abs(theta) < 0.0001:

# sin(x) = x − x^3/3! + ...

# sin(f x) / sin(x)

# = ((fx) − (fx)^3/3! + ...) / (x − x^3/3! + ...)

# ~= ((fx) − (fx)^3/3!) / (x − x^3/3!)

# = (f − f(fx)^2/3!) / (1 − x^2/3!)

# = f (1 − f^2 x^2/6) / (1 − x^2/6)

d = theta * theta / 6

return factor * (1 − d * factor * factor) / (1 − d)

return math.sin(theta * factor) / math.sin(theta)

The above method will be applied at the method for full transformation, when a spherical transformation is being carried out. In order to make an angular interpolation the obvious shall be carried out: the difference between the two angles is learned, care should be taken to recourse to a roundabout way and then a linear transformation should be made. To take correctly the sign of the difference is a difficult task, but it is already explained. When everything is put together, we obtain:

defquantum_unitary_lerp(u1, u2, t):

Interpolates between two 2x2 unitary NumPy matrices.

# Split into rotation and phase parts

q1, p1 = quantum_unitary_breakdown(u1)

q2, p2 = quantum_unitary_breakdown(u2)

# Spherical transformation of the rotation

dot = sum(v1*v2 for v1,v2 in zip(q1, q2))

if dot < 0:

# Not to be made in the long way around...

q2 *= −1

p2 *= −1

dot *= −1

theta = math.acos(min(dot, 1))

c1 = sin_scale_ratio(theta, 1−t)

c2 = sin_scale_ratio(theta, t)

u3 = (u1 * c1 / p1 + u2 * c2 / p2)

# Angular transformation of the phase

a1 = np.angle(p1)

a2 = np.angle(p2)

# The smallest angular distance with a sign (mod 2pi)

da = (a2 − a1 + math.pi) % (math.pi * 2) − math.pi

a3 = a1 + da * t

p3 = math.cos(a3) + 1j * math.sin(a3)

return u3 * p3

Demonstration

Below is given a demonstration of the described above method with the developed by the author of the article quantum simulator (Figure 2). Matrices for start and end can be entered in the text boxes and (after the entered

matrices are adjusted, they should be unitary) a continuous transition between the two matrices is shown. It is difficult to be checked ostensibly, whether the intermediate matrices are unitary, but it can be seen that the movement is smooth and the colored area remains relatively constant.

4. Conclusion

Single qubit operations are a lot like rotations, but with an added phase coefficient. This fact can be used to create a method for linear transformation between 2 unitary matrices. The method described above, works, but is not optimal. For example, it does not ensure a constant angular speed. Also, in some cases it doesn’t take the shortest possible path. The common method for mapping rotations into unitary matrices is smooth, but cannot generate the Pauli matrices and requires a 720˚ turn to get back to the starting point. By applying a phase correction, we can fix those issues, but we are forced to introduce a phase discontinuity with the respect to the axis of rotation.

Cite this paper

NikolayRaychev, (2015) Bilaterally Symmetrical Transformation between Independent Operators and Rotations. Journal of Quantum Information Science,05,79-88. doi: 10.4236/jqis.2015.53010

References