Journal of Quantum Information Science
Vol.04 No.04(2014), Article ID:52398,5 pages
10.4236/jqis.2014.44018
Reply to “Comments on ‘There Is No Axiomatic System for the Quantum Theory’”
Koji Nagata
13-3 West 6 South 27, Obihiro, Hokkaido, Japan
Email: ko_mi_na@yahoo.co.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 October 2014; revised 15 November 2014; accepted 3 December 2014
ABSTRACT
Barros discusses that [Jose Acacio de Barros, Int. J. Theor. Phys. 50, 1828 (2011)] Nagata derives inconsistencies from quantum mechanics [K. Nagata, Int. J. Theor. Phys. 48, 3532 (2009)]. Barros considers that the inconsistencies do not come from quantum mechanics, but from extra assumptions about the reality of observables. Here we discuss the fact that there is a contradiction within the quantum theory. We discuss the fact that only one expected value in a spin-1/2 pure state 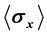 rules out the reality of the observable. We do not accept extra assumptions about the reality of observables. We use the actually measured results of quantum measurements (raw data). We use a single Pauli observable. We stress that we can use the quantum theory even if we give up the axiomatic system for the quantum theory.
rules out the reality of the observable. We do not accept extra assumptions about the reality of observables. We use the actually measured results of quantum measurements (raw data). We use a single Pauli observable. We stress that we can use the quantum theory even if we give up the axiomatic system for the quantum theory.
Keywords:
Quantum Measurement Theory, Quantum Computer, Formalism

1. Introduction
Barros discusses that [1] Nagata derives inconsistencies from quantum mechanics [2] . Barros considers that the inconsistencies do not come from quantum mechanics, but from extra assumptions about the reality of observables. More clearly, since quantum mechanics forbids the simultaneous measurements of non-commuting observables, as they do not commute, it does not allow us to simultaneously assign values to them. The contradiction does not come from quantum mechanics, but from the assumption that we can assign values to measurements that were not performed.
Here we discuss the fact that there is a contradiction within the quantum theory. We discuss the fact that only one expected value of a spin-1/2 pure state 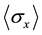 rules out the reality of the observable. We do not accept extra assumptions about the reality of observables. We use the actually measured results of quantum measurements (raw data). We use a single Pauli observable. We stress that we can use the quantum theory even if we give up the axiomatic system for the quantum theory.
rules out the reality of the observable. We do not accept extra assumptions about the reality of observables. We use the actually measured results of quantum measurements (raw data). We use a single Pauli observable. We stress that we can use the quantum theory even if we give up the axiomatic system for the quantum theory.
On the other hand, the double-slit experiment [3] is an illustration of wave-particle duality. In it, a beam of particles (such as photons) travels through a barrier with two slits removed. If one puts a detector screen on the other side, the pattern of detected particles shows interference fringes characteristic of waves; however, the detector screen responds to particles. The system exhibits the behavior of both waves (interference patterns) and particles (dots on the screen).
If we modify this experiment so that one slit is closed, no interference pattern is observed. Thus, the state of both slits affects the final results. We can also arrange to have a minimally invasive detector at one of the slits to detect which slit the particle went through. When we do that, the interference pattern disappears [4] . An analysis of a two-atom double-slit experiment based on environment-induced measurements is reported [5] .
We assume implementation of the double-slit experiment. There is a detector just after each slit. Thus interference figure does not appear, and we do not consider such a pattern. The possible values of the result of measurements are 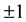 (in
(in 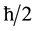 unit). If a particle passes one side slit, then the value of the result of measurement is +1. If a particle passes through another slit, then the value of the result of measurement is −1. This model is an easy detector model for Pauli observable.
unit). If a particle passes one side slit, then the value of the result of measurement is +1. If a particle passes through another slit, then the value of the result of measurement is −1. This model is an easy detector model for Pauli observable.
Projective measurement theory does not meet Deutsch’s algorithm [6] . In this reference, the expected values of the two spin observables 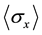 and
and 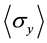 cannot be measured by using projective measurement theory. And new measurement theory covers the problem. Let us follow the argumentations. Assume a pure spin-1/2
cannot be measured by using projective measurement theory. And new measurement theory covers the problem. Let us follow the argumentations. Assume a pure spin-1/2
state lying in the 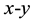 plane. We have
plane. We have 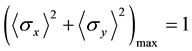 from the wave functional analysis of quantum mechanics. On the other hand, we have
from the wave functional analysis of quantum mechanics. On the other hand, we have 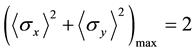 if projective measurement theory is true. This fact cannot coexist with quantum formula
if projective measurement theory is true. This fact cannot coexist with quantum formula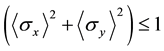 . Hence the expected values of two spin ob-
. Hence the expected values of two spin ob-
servables 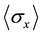 and
and 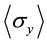 cannot be measured by using projective measurement theory. But, we have
cannot be measured by using projective measurement theory. But, we have
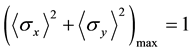 when the new quantum measurement theory is true. The values of the result of quantum
when the new quantum measurement theory is true. The values of the result of quantum
measurements are . We consider whether an expected value of one spin observable
. We consider whether an expected value of one spin observable 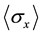 can be measured by using projective measurement theory. So, we investigate the relation between an easy detector model for Pauli observable and projective measurement theory.
can be measured by using projective measurement theory. So, we investigate the relation between an easy detector model for Pauli observable and projective measurement theory.
We consider whether projective measurement theory meets an easy detector model for Pauli observable. We try to implement double-slit experiment. There is a detector just after each slit. Thus interference figure does not appear, and we do not consider such a pattern. We assume that a source of spin-carrying particles emits them in a state, which can be described as an eigenvector of Pauli observable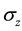 . We consider a single expected value of Pauli observable
. We consider a single expected value of Pauli observable 

At this stage we are in the following situation.
・ We cannot measure an expected value of a single spin observable in a state by using projective measurement theory.
2. There Is a Contradiction within the Quantum Theory by Using Joint Probability
First we discuss a contradiction within the quantum theory as follows [7] .
Matrix theory is not compatible with probability theory. Matrix theory has axioms. Probability theory has axioms. These have axioms without a contradiction. Can we construct axioms for matrix theory and probability theory without a contradiction?
Let us consider joint probability. 




We consider as follows: First we measure observable 






On the other hand, the joint probability is depictured in terms of conditional probabilities:

From axioms of probability theory, we have

We cannot assign truth value “1” for the proposition (2) and for the proposition (4), simultaneously. We are in a contradiction. We cannot construct axioms for matrix theory and probability theory without the contradiction. There is a contradiction within the quantum theory.
The first point is actually that, conventional Quantum Mechanics discussions typically do not employ conditional probabilities correctly if at all. This is the central issue with Bell’s analysis leading to the idea that Quantum Mechanics requires non-locality or irreality and wave packet collapse and what not!
3. Does Pauli Observable in a Quantum State Have a Counterpart in Physical Reality?
The two expected values of a spin-1/2 pure state 

In this section, we discuss the fact that only one expected value of a spin-1/2 pure state 
We assume implementation of the double-slit experiment [3] . There is a detector just after each slit. Interference figure does not appear, and we do not consider such a pattern. Let 


We consider a quantum expected value 

We introduce a hidden-variables theory for the quantum expected value of the Pauli observable

where 







In what follows, we discuss the fact that we cannot assign the truth value “1” for the proposition (6). Assume the proposition (6) is true. We have the same proposition

An important note here is that the value of the right-hand-side of (6) is equal to the value of the right-hand- side of (7) because we only change a label.
We derive a necessary condition for the quantum expected value given in (6). We derive the possible value of the product 


Here we use the fact

since the possible values of 


We derive a necessary condition for the quantum expected value for the system in a pure spin-1/2 state 




We do not assign the truth value “1” for two propositions (10) and (12), simultaneously. We are in a contradiction. We have to give up a hidden-variables theory for the expected value of the Pauli observable

4. There Is a Contradiction within the Quantum Theory by Using a Single Pauli Observable
Next we discuss the fact that there is a contradiction within the quantum theory by using a single Pauli observable [8] . In this case, there is no need to argue that observables under consideration are commuting or non-com- muting. Especially, we systematically describe our assertion based on more mathematical analysis using raw data (the actually measured results of quantum measurements). In this case, there is no need to argue the reality of observables. There exists raw data because we have seen it.
We consider the relation between double-slit experiment and projective measurement. We try to implement double-slit experiment. There is a detector just after each slit. Thus interference figure does not appear, and we do not consider such a pattern. The actually measured results of quantum measurements are 

4.1. A Wave Function Analysis
Let 




The above quantum expected value is zero if we consider only a wave function analysis.
We derive a necessary condition for the quantum expected value for the system in the pure spin-1/2 state 



4.2. Projective Measurement
On the other hand, a mean value 

where 





Assume the quantum mean value with the system in an eigenvector 


We can assume as follows by Strong Law of Large Numbers1,

In what follows, we show that we cannot assign the truth value “1” for the proposition (16) concerning projective measurement.
Assume the proposition (16) is true. By changing a label 


An important note here is that the actually measured value of the right-hand-side of (16) is equal to the actually measured value of the right-hand-side of (18) because we only change the label. We have

Here 

Thus we derive a proposition concerning the quantum mean value under an assumption that projective measurement is true (in a spin-1/2 system), that is

From Strong Law of Large Numbers, we have

Hence we derive the following proposition concerning projective measurement

We do not assign the truth value “1” for two propositions (14) (concerning a wave function analysis) and (23) (concerning projective measurement), simultaneously. We are in a contradiction.
We cannot accept the validity of the proposition (16) (concerning projective measurement) if we assign the truth value “1” for the proposition (14) (concerning a wave function analysis). In other words, such projective measurement does not meet the detector model for spin observable
We note here that there is much nonsense in the Physics literature regarding the theoretical formality for Spin. The formalism is correct so long as only one dimension is under consideration---a restriction that is fully acceptable in view of the fact that to engage spin empirically a Magnetic (B) field is required and it can have only one direction at the point of interacting with a charge. All formal talk of the spin of a particle in both the 


5. Conclusion
In conclusions, Barros has discussed that Nagata has derived inconsistencies from quantum mechanics. Barros has considered that the inconsistencies do not come from quantum mechanics, but from extra assumptions about the reality of observables. Here we have discussed the fact that there is a contradiction within the quantum theory. We have discussed the fact that only one expected value of a spin-1/2 pure state 
Acknowledgements
The author thanks Professor Tadao Nakamura.
References
- Acacio de Barros, J. (2011) Comments on “There Is No Axiomatic System for the Quantum Theory”. International Journal of Theoretical Physics, 50, 1828-1830. http://dx.doi.org/10.1007/s10773-011-0696-z
- Nagata, K. (2009) There is No Axiomatic System for the Quantum Theory. International Journal of Theoretical Physics, 48, 3532-3536. http://dx.doi.org/10.1007/s10773-009-0158-z
- Wikipedia (2014) Double-Slit Experiment. http://en.wikipedia.org/wiki/Double-slit_experiment
- Wikipedia (2014) De Broglie-Bohm Theory.http://en.wikipedia.org/wiki/De_Broglie%E2%80%93Bohm_theory
- Schon, C. and Beige, A. (2001) Analysis of a Two-Atom Double-Slit Experiment Based on Environment-Induced Measurements. Physical Review A, 64, Article ID: 023806. http://dx.doi.org/10.1103/PhysRevA.64.023806
- Nagata, K. and Nakamura, T. (2010) Can von Neumann’s Theory Meet the Deutsch-Jozsa Algorithm? International Journal of Theoretical Physics, 49, 162-170. http://dx.doi.org/10.1007/s10773-009-0189-5
- Nagata, K. and Nakamura, T. (2013) An Additional Condition for Bell Experiments for Accepting Local Realistic Theories. Quantum Information Processing, 12, 3785-3789. http://dx.doi.org/10.1007/s11128-013-0635-4
- Nagata, K. and Nakamura, T. (2013) Von Neumann’s Theory Does Not Meet Deutsch’s Algorithm. Precision Instrument and Mechanology, 2, 104.
NOTES
1In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed. The strong law of large numbers states that the sample average converges almost surely to the expected value.




