Journal of Quantum Information Science
Vol.4 No.1(2014), Article ID:42930,17 pages DOI:10.4236/jqis.2014.41001
Effect of the Spin-Orbit Interaction (Heisenberg XYZ Model) on Partial Entangled Quantum Network
Abdel-Haleem Abdel-Aty1, Nordin Zakaria1, Lee Yen Cheong2, Nasser Metwally3
1Computer and Information Science Department, Universiti Teknologi Petronas, Tronoh, Malaysia
2Fundamentals and Applied Science Department, Universiti Teknologi Petronas, Tronoh, Malaysia
3Mathematics Department, College of Science, University of Bahrain, Sakhir, Kingdom of Bahrain
Email: amahmedit@yahoo.com, ah.mohamed_g01719@utp.edu.my
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 16 November 2013; revised 6 January 2014; accepted 28 January 2014
ABSTRACT
Dzyaloshiniskii-Moriya (DM) interaction in three directions (Dx, Dy and Dz) is used to generate entangled network from partially entangled states in the presence of the spin-orbit coupling. The effect of the spin coupling on the entanglement between any two nodes of the network is investigated. The entanglement is quantified using Woottores concurrence method. It is shown that the entanglement decays as the coupling increases. For larger values of the spin coupling, the entanglement oscillates within finite bounds. For the initially entangled channels, the upper bound does not exceed its initial value, whereas the entanglement reaches its maximum value for the channels generated via indirect interaction.
Keywords:Quantum Network; Entanglement; Spin-Orbit Interaction

1. Introduction
Quantum Information Technology (QIT) promises faster and more secure means of data manipulation by making use of the quantum properties of matter [1] -[5] . The quantum network is a fast growing field in quantum information Technology. Specifically, a quantum network consists of quantum nodes connected by quantum channels [6] . The quantum nodes generate, process, and store information encoded in the quantum states of a physical system [7] . The information is exchanged through quantum channels by way of sending photons from one node to the other, or through quantum entanglement shared by the nodes [8] -[10] . The importance of the quantum networks increased in the past few years in regards to the problems in the classical networks like the security of the information, privacy and the speed of the transmission of information. Quantum networks have been implemented experimentally [11] -[14] and theoretically [15] -[19] .
The Dzyaloshiniskii-Moriya (DM) interaction is a natural phenomena discovered in 1960 by Moriya Dzyaloshinskii-Moriya (DM) as an antisymmetric and anisotropic exchange coupling between two spins) [20] [21] . It is found that the DM interaction strengthen the entanglement among particles implies that the DM interaction plays an important role in the generation of the quantum entanglement in the field of quantum networks [22] . The quantum correlation as a result of the DM interaction between two particles is investigated by many authors (see for examples [23] -[25] ). The thermal entanglement between two qubits in the Heisenberg XYZ model and the effect of the DM interaction and its strength are discussed by Da Chuang and Z. Liang Cao [26] . The effect of the intrinsic decoherence in the teleportation of two qubits XYZ model is studied in the presence of DM interaction [27] . Entanglement sudden death and birth of the qubit-qutrit pair under DM interaction [28] and the effect of the spin-orbit interaction in the dynamics of the entanglement in the presence of DM interaction [29] -[31] are investigated recently.
Metwally [15] introduced a theoretical protocol to generate multi-nodes quantum network by using maximum entangled states, where the terminals of each disconnected node are connected via DM interaction. Theoretical quantum network model with “d” level system is constructed and gives important results in many useful applications in quantum network environment [32] . The possibility of generating entangled network by using a class of partially entangled network is discussed by Abdel-Aty et al. [16] . Also, as a development of our last quantum network we studied the possibility of the generation of quantum network with the DM interaction is switched to more than one direction. The quantum teleportation is investigated over this quantum network as well [17] . Therefore, we are motivated to investigate the effect of the spin-orbit and the efficiency of the generated entangled network in the presence of DM interaction.
In this paper, we introduce the model and its evolution in Section 2. The entanglement between different nodes is quantified for different values of the spin-orbits coupling and the DM’s strength is discussed in Section 3. We then summarize our results and discussion in Section 4.
2. The Model
It is assumed that entangled network consists of four nodes is generated by using partial entangled states of Werner type [16] [33] . In the suggested quantum network the node “1” and node “2” is initially connected as well as node “3” and “4” (solid line). The dash line between the node “2” and node “3” represents the connections which generated by the DM (x, y and z) interaction with the effect of the spin orbit coupling Jx, Jy and Jz as seen in Figure 1.
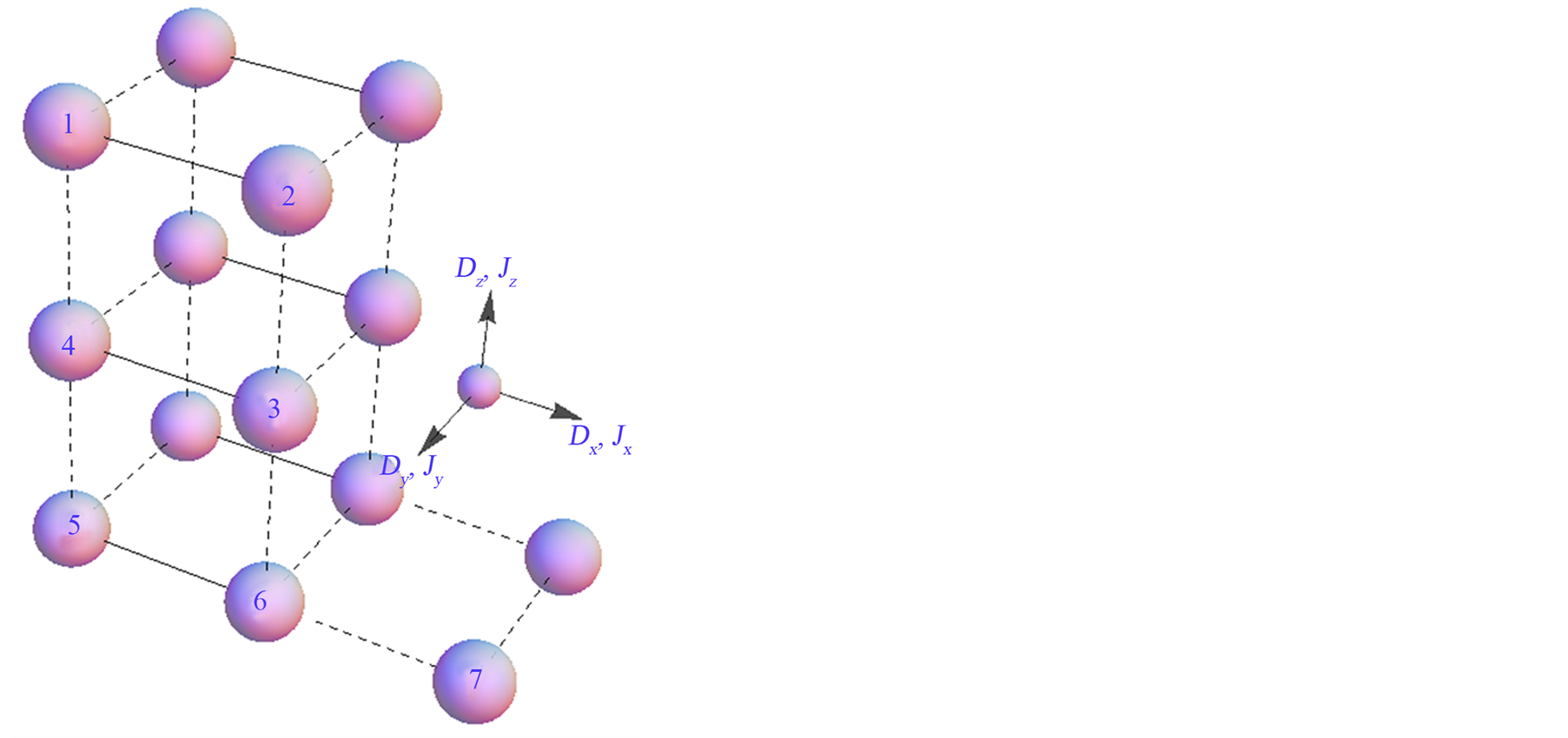
Figure 1. Our suggested quantum network.
Consider a partial entangled state generated by a source of the form
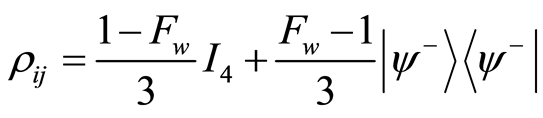 (1)
(1)
where  is the singlet Bell state and Fw is the maximum fraction corresponding to the Werner-state.
is the singlet Bell state and Fw is the maximum fraction corresponding to the Werner-state.
The initial state of the total system is given by
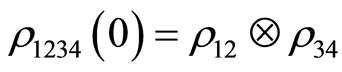 (2)
(2)
The evolution of the initial state (2) is given by,
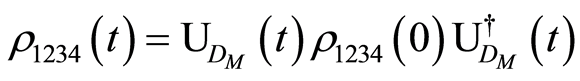 (3)
(3)
where 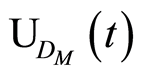 is the unitary operator and can be written as
is the unitary operator and can be written as
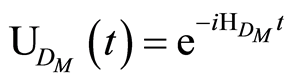 (4)
(4)
where 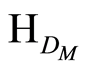 is the Hamiltonian of the DM (x, y and z) interaction which rules the interactions as you will see in Sections (2.1, 2.2 and 2.3).
is the Hamiltonian of the DM (x, y and z) interaction which rules the interactions as you will see in Sections (2.1, 2.2 and 2.3).
2.1. Heisenberg XYZ Model with Dx
The Hamiltonian describing the evolution of the system for a two-qubit spin-orbit chain with the DM interaction is switched on the x-axis can be written as
 (5)
(5)
where k, l represent the nodes which are connected together via DM interaction with x-component of strength Dx; Jx, Jy and Jz are the x, y and z-component of the real coupling coefficients, respectively, and the  is the Pauli matrices
is the Pauli matrices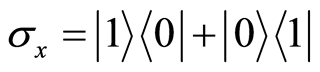 ,
,  and
and 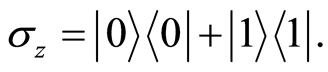 In our case k and l represent the second and third qubit, respectively.
In our case k and l represent the second and third qubit, respectively.
The final density operator of the network is given by
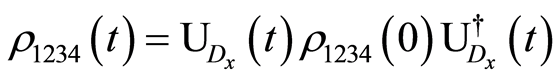 (6)
(6)
where
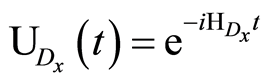 (7)
(7)
is the unitary operator which can be written explicitly in the basis 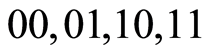 as
as
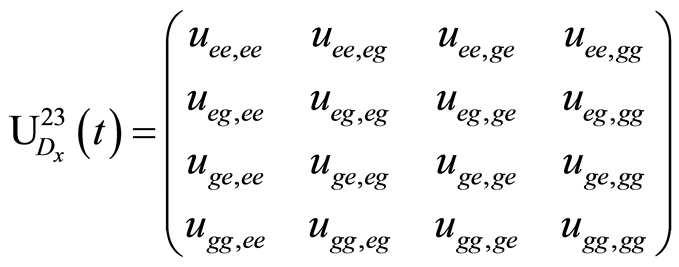 (8)
(8)
where
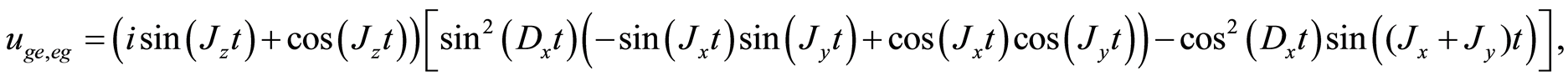

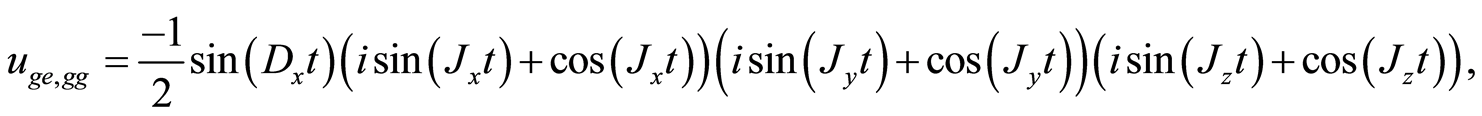

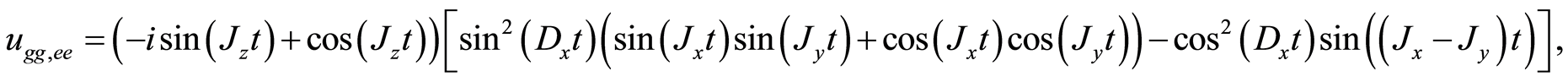

And the rest of the components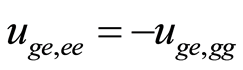 ,
, 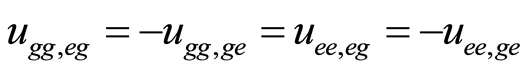 ,
,  ,
,  ,
, 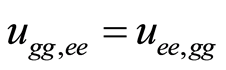 and
and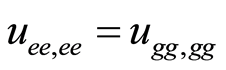 . Using Equations (6) and (8), one obtains the final entangled network between four nodes. Since that we are interested to quantify the degree of entanglement between different nodes, one can obtain the required density operator between each pair of nodes by tracing out the other two. For example, the density operator between the first and the second node is given by
. Using Equations (6) and (8), one obtains the final entangled network between four nodes. Since that we are interested to quantify the degree of entanglement between different nodes, one can obtain the required density operator between each pair of nodes by tracing out the other two. For example, the density operator between the first and the second node is given by 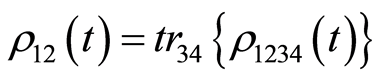 and so forth.
and so forth.
2.2. Heisenberg XYZ Model with Dy
Similarly, the Hamiltonian describing the evolution of the system when the interaction is switched to the y-direction can be written as.
 (9)
(9)
In this case, the unitary operator is given by
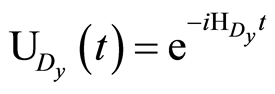 (10)
(10)
In matrix form, the unitary operator Equation (10) can be written as a matrix Equation (8) and the elements of the matrix are:



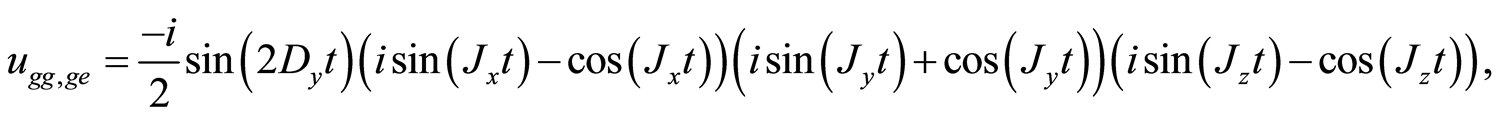


And the rest of the components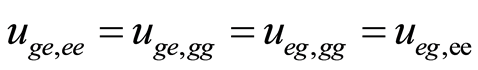 ,
,  ,
,  ,
,  ,
,  and
and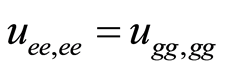 .
.
2.3. Heisenberg XYZ Model with Dz
Similarly, the Hamiltonian describing the evolution of the system when the interaction is switched to the z-direction can be written as.
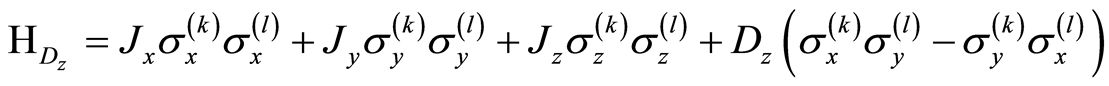 (11)
(11)
In this case, the unitary operator is given by
 (12)
(12)
Is the unitary operator which used to connect between particle “2” and “3” when the interaction is switched on y-axis and defined by
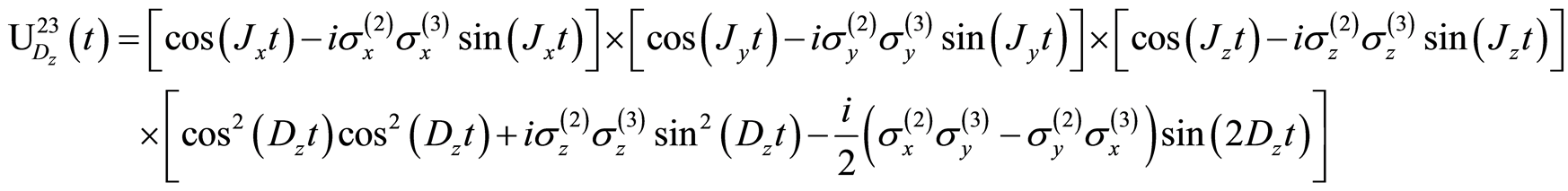 (13)
(13)
In matrix form, the unitary operator Equation (13) can be written as in Figure 8.
Where the elements of the matrix are:


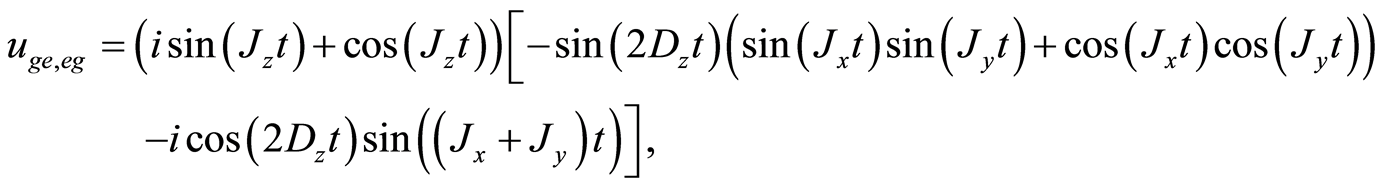
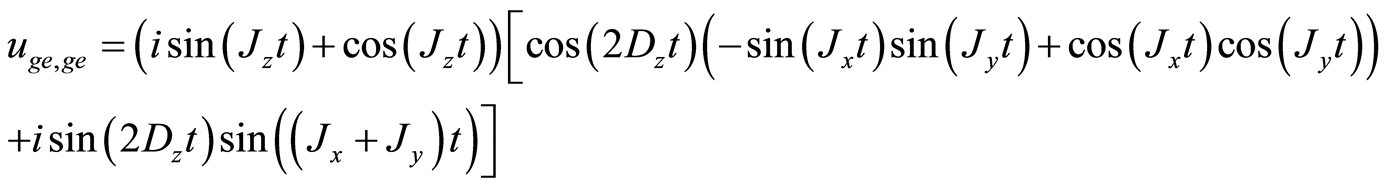
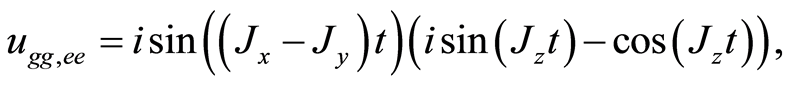

And the rest of the components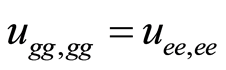 ,
,  and
and 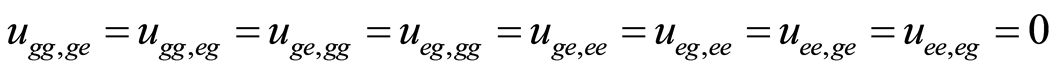
3. Results and Discussion
In this section, we quantify the entanglement between each pair of nodes. Practically, we consider the channels , where ij = 12, 13 and 14. For this purpose, we use Wootters’s concurrence as a measure for the entanglement [34] which is defined by
, where ij = 12, 13 and 14. For this purpose, we use Wootters’s concurrence as a measure for the entanglement [34] which is defined by
 (14)
(14)
where 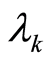 (k = 1, 2, 3, 4) is the eigen values of the matrix
(k = 1, 2, 3, 4) is the eigen values of the matrix 
The entanglement behavior (concurrence) of the entangled state between nodes “1” and “2”,  , is described in Figure 2 for different coupling values Ji (i= x, y, z), and the strength of DM is assumed to be fixed, Dx = 0.2. Figure 2(a) depicted the evolution of the concurrence C in the presence of zero coupling or one and only one non-zero coupling. In this case, the hamiltonian will be convert to
, is described in Figure 2 for different coupling values Ji (i= x, y, z), and the strength of DM is assumed to be fixed, Dx = 0.2. Figure 2(a) depicted the evolution of the concurrence C in the presence of zero coupling or one and only one non-zero coupling. In this case, the hamiltonian will be convert to . It is clear that for Jx=Jy=Jz, the concurrence decays gradually to its minimum bound (C = 0.4) and then increased to maximum bound without exceeding the initial bounds. This shows that the decay is coming from the interaction be-
. It is clear that for Jx=Jy=Jz, the concurrence decays gradually to its minimum bound (C = 0.4) and then increased to maximum bound without exceeding the initial bounds. This shows that the decay is coming from the interaction be-
 (a)
(a) (b)
(b) (c)
(c)
Figure 2. The entanglement, C12, between node “1” and node “2” (a) the solid red line for Jx = Jy =Jz = 0 without the effect of spin), the black dotted line for (Jx = 0.5 and Jy = Jz = 0,) green line for (Jy = 0.5 and Jx = Jz = 0), blue dashed line for ( Jx = Jy =0 and Jz = 0.5) and Dx = 0.2. (b) Similar to (a) but the solid red line for (Jx = Jy = 0.5 and Jz = 0), black dotted for (Jx = Jy = 0.5 and Jz = 0), green line for (Jx = 0 and Jy = Jz = 0.5), blue dashed for (Jx = Jy = Jz = 0.5) and Dx = 0.2. (c) The red line represents the entanglement for (Jx = Jy = Jz = 0.1), green dashed for (Jx = Jy = Jz = 0.3) and the blue dashed line for (Jx = Jy = Jz = 0.5) and Dx = 0.2.
tween the second and third node, and consequently some correlations are lost. However, the upper and lower bounds will depend on the non-zero coupling when it is switched on. This behavior shows that the minimum bound of C for Jx ¹ 0 is always larger than that depicted for Jy ¹ 0 or Jz ¹ 0. On the other hand, the concurrence vanishes completely for Jy ¹ 0 or Jz ¹ 0, i.e., C = 0 as the scaled time increased without exceeding the initial upper limit [13] [14] . In Figure 2(c), we investigate the behavior of the concurrence for Jx = Jy = Jz ¹ 0. It can be seen that when the coupling parameters are small, Jx = Jy = Jz = 0.1, the concurrence C decays gradually and vanishes when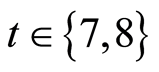 . For larger values of Ji (i = x, y, z), the concurrence decays comparably faster.
. For larger values of Ji (i = x, y, z), the concurrence decays comparably faster.
Figure 2(b) describes the behavior of the concurrence for the entangled state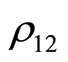 , where two non-zero couplings are considered. The general behavior is similar to the one that is depicted in Figure 2(a), but the number of oscillation increased within the bounds. If we compare the solid curves in the Figures 2(a) and (b), we see that the presence of the coupling causes the concurrence to decay quicker.
, where two non-zero couplings are considered. The general behavior is similar to the one that is depicted in Figure 2(a), but the number of oscillation increased within the bounds. If we compare the solid curves in the Figures 2(a) and (b), we see that the presence of the coupling causes the concurrence to decay quicker.
Figure 3 describes the behavior of the concurrence for the entangled state which is generated between nodes “1” and “3” via indirect interaction. Figure 3(a) describes the behavior of C for non-zero coupling where the same values of the coupling and DM’s strength as considered in Figure 2 are being used. Since the two nodes are initially disentangled, the concurrence C = 0 at t = 0. As soon as the interaction is switched on and the entangled state is generated between the first and the third node, the concurrence increased towards the upper bound (C = 0.4). As t continues to elapse, the concurrence decays and vanishes completely. This behavior is repeated periodically.
The dynamics of concurrence, C, for the channel , when two non-zero couplings are considered is depicted in Figure 3(b). The values of Ji, where i = x, y, z are the same as in Figure 2(b). This figure shows that the concurrence oscillates between bounded limits. The phenomena of the sudden-death and sudden-birth appeared in the entanglement are shown clearly.
, when two non-zero couplings are considered is depicted in Figure 3(b). The values of Ji, where i = x, y, z are the same as in Figure 2(b). This figure shows that the concurrence oscillates between bounded limits. The phenomena of the sudden-death and sudden-birth appeared in the entanglement are shown clearly.
Figure 3(c) describes the behavior of C for the state 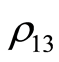 when Jx = Jy = Jz ¹ 0 have the same values as in Figure 2(c). It is clear that the general behavior is similar to that as depicted in Figure 3(b), but the number of oscillation increased as the value of the coupling increased. We note that the upper bound is slightly larger when Ji is large.
when Jx = Jy = Jz ¹ 0 have the same values as in Figure 2(c). It is clear that the general behavior is similar to that as depicted in Figure 3(b), but the number of oscillation increased as the value of the coupling increased. We note that the upper bound is slightly larger when Ji is large.
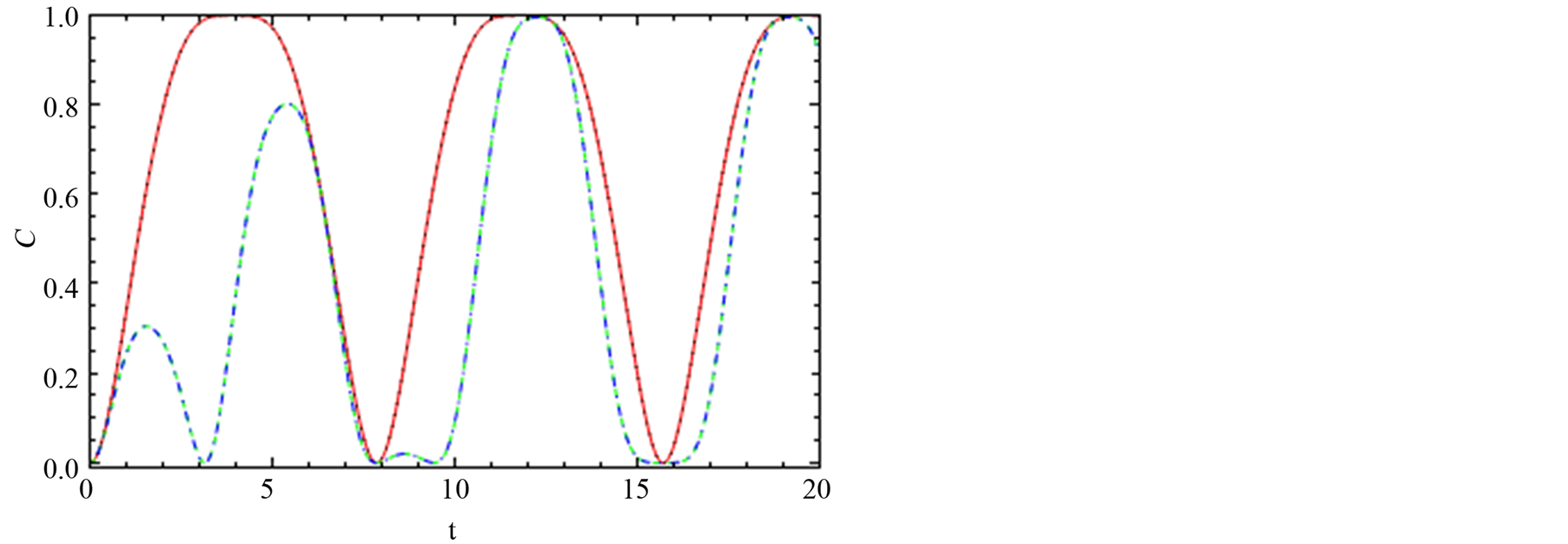
We investigate the behavior of the entanglement for state 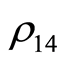 generated via indirect interaction, is shown in Figures 4(a)-(c). It is clear that the behavior of C is similar to that displayed for
generated via indirect interaction, is shown in Figures 4(a)-(c). It is clear that the behavior of C is similar to that displayed for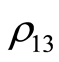 . However, the upper bound for the state
. However, the upper bound for the state 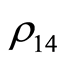 is much larger and reaches maximum value at C = 1. The number of oscillation of the concurrence increased as the spin-orbit coupling increased.
is much larger and reaches maximum value at C = 1. The number of oscillation of the concurrence increased as the spin-orbit coupling increased.
On the other hand, the oscillation increased if all the couplings have non-zero values.
The dynamics of the entanglement in the quantum network when the interaction is switched on y-direction is shown in Figures 5-7. Figure 5 represents the entanglement over channel “12” with different values of the spin-orbit coupling. The parameters used in Figure 5(a) are identical to the one used in Figure 2(a) but the interaction is switched on y-axis with fixed Dy = 0.2. It is shown that when Jx = Jy = Jz = 0, the Hamiltonian represents the normal case without the effect of spin-orbit coupling has the form  is represented by the solid red line [16] . The black dotted line illustrates the effect of the spin-orbit at Jx = 0.5 and Jy = Jz = 0. It is shown that the concurrence started from the maximum value at C = 0.62 and the entanglement decreased quickly as time goes on. The effect of spin-orbit Jz = 0.5 is shown by the dotted blue line which is similar to the black dotted line. The green dashed line represents the effect of Jy = 0.5 and Jx = Jz = 0. The entanglement shows similar behavior to the case when spin-orbit effect is ignored but a slight different to the amplitude of the entanglement.
is represented by the solid red line [16] . The black dotted line illustrates the effect of the spin-orbit at Jx = 0.5 and Jy = Jz = 0. It is shown that the concurrence started from the maximum value at C = 0.62 and the entanglement decreased quickly as time goes on. The effect of spin-orbit Jz = 0.5 is shown by the dotted blue line which is similar to the black dotted line. The green dashed line represents the effect of Jy = 0.5 and Jx = Jz = 0. The entanglement shows similar behavior to the case when spin-orbit effect is ignored but a slight different to the amplitude of the entanglement.
Figure 5(b) shows the effect of the spin-orbit interaction in two different directions. In this figure, the curves is initially started from its maximum and then the entanglement decreased to zero at t = 1. Then, the entanglement is increased again and reaches C = 0.4 at t = 2.5. One observes that the entanglement is influenced by the spin-orbit and the number of oscillations is increased.
The effect of Jx, Jy and Jz in the dynamics of the entanglement over channel “12” is depicted in Figure 5(c). This figure shows that the dynamics of the entanglement can be influenced by the values of the total spin-orbit interaction where the oscillation is increased by increasing the value of the spin-orbit. Here the solid red line represents the dynamics of the entanglement for Jx = Jy = Jz = 0.1, the dashed green line is produced by Jx = Jy = Jz = 0.3 and the dotted blue line is produced by Jx = Jy = Jz = 0.5.
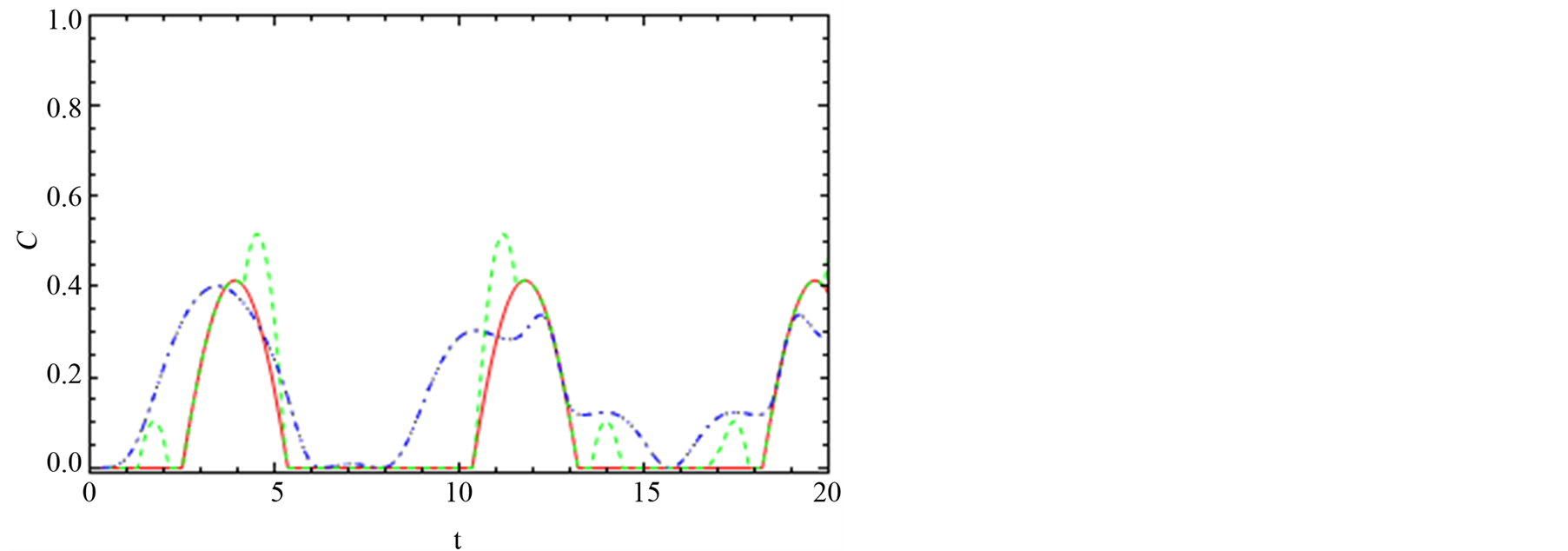
The dynamics of the entanglement on channel “13” with the effect of the spin-orbit interaction when DM interaction is switched on the y-axis. Figure 6(a) is similar to Figure 3(a) without the effect of the spin-orbit inte-
 (a)
(a)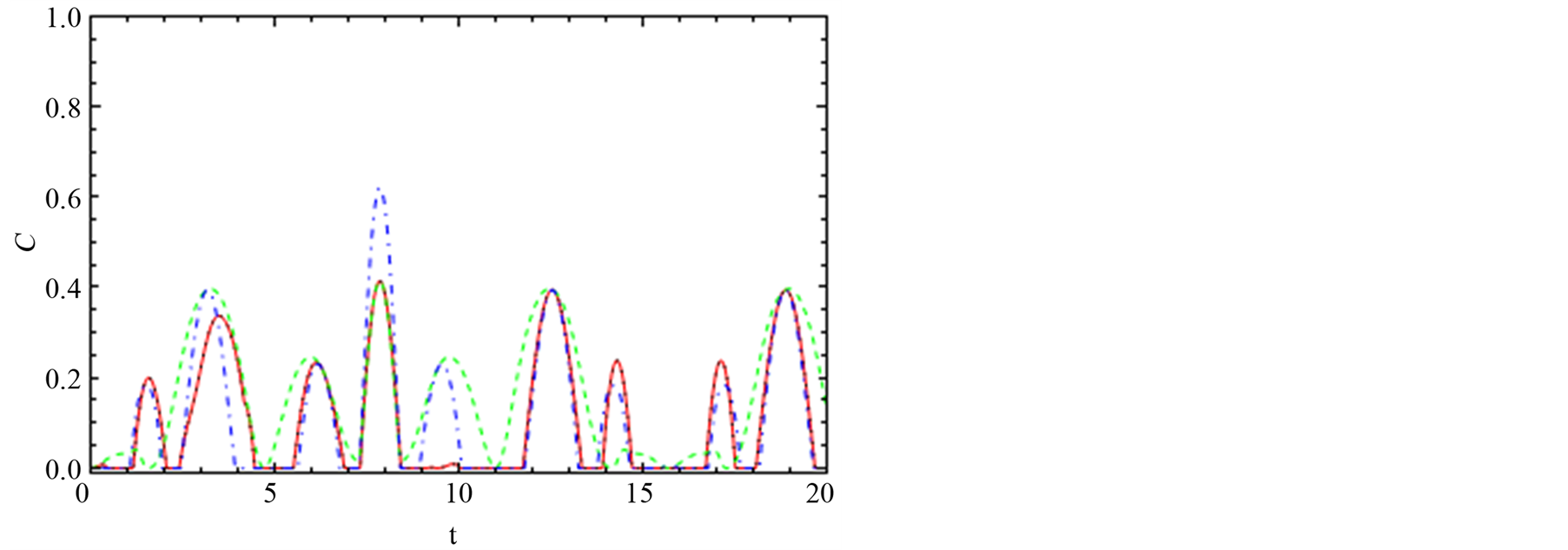 (b)
(b) (c)
(c)
Figure 3. The dynamics of the entanglement, C13, between node “1” and node “3”. Figures (a), (b) and (c) have the same feature with Figure 2 but reside in channel “13”.
raction. It is clear that there is no entanglement at the initial stage during the interaction period. The entanglement appeared at t = 2.5 and reaches its maximum at t = 3.75 and then vanishes after t = 5. It remains zero there until t = 10 and the same behavior is repeated periodically. The effect of x-spin-orbit is depicted by the dotted black line which has the same effect as the z-spin-orbit interaction to which the generation of the entanglement started at t = 1, and the generation of entanglement without spin-orbit is started at t = 2.5. The maximum value of the entanglement is 0.4 at t = 3. It decreased to zero at t = 6 and increased again after t = 8 up to maximum at t = 12. The effect of the y-spin orbit interaction is represented by the dashed green line.
 (a)
(a) (b)
(b)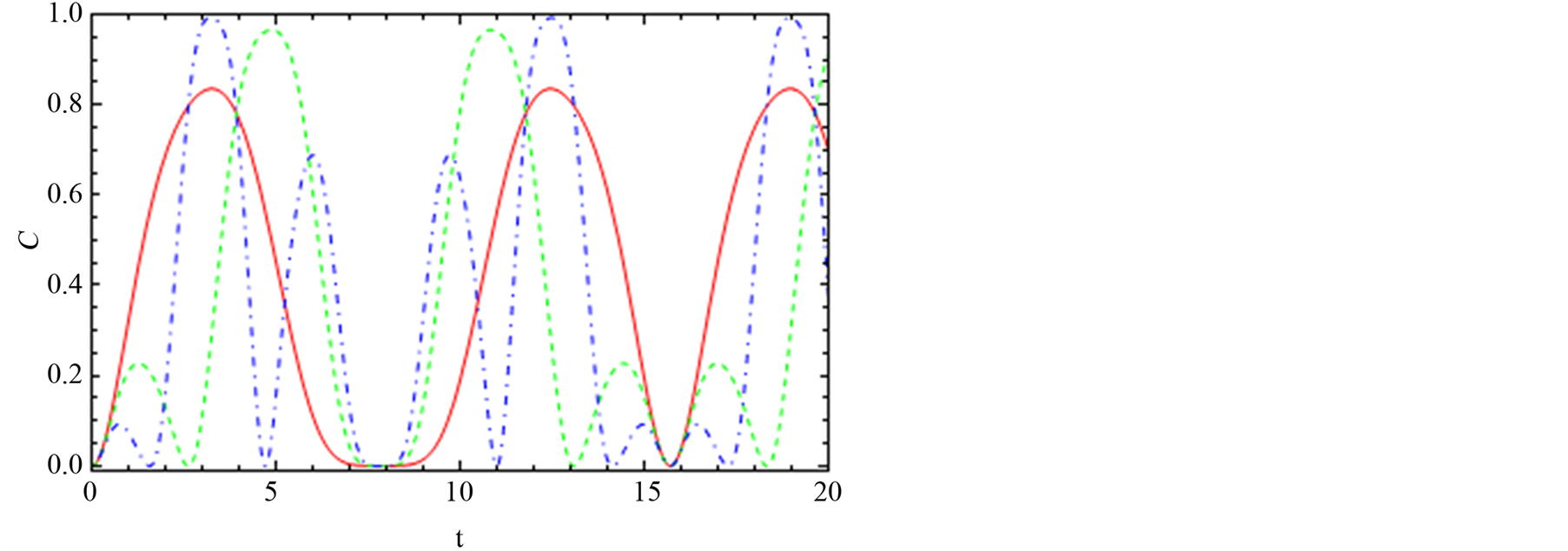 (c)
(c)
Figure 4. The dynamics of the entanglement, C14, between node “1” and node “4”. Figures (a), (b) and (c) have the same feature with Figure 2 but reside in channel “14”.
Figure 6(b) is similar to Figure 5(b) for the channel “13”. This figure shows that the effects of Jx = Jy = 0.5 (solid red line) and of Jy = Jz = 0.5 (dashed green line) are same where the entanglement increased from zero after t = 1 and reaches 0.2 at t = 1.5. It then decays exponentially. The effects of the Jy = Jz = 0.5 (dotted black line) and of the Jx = Jy = Jy = 0.5 (dashed blue line) are similar where the entanglement started to generate at t = 0.5 and increased to maximum at t = 2. It then decreased to zero at t = 6. One observes that the shape of the entanglement becomes different due to different values of the spin-orbit interaction. Figure 6(c) shows the effect the total spin in the dynamics of entanglement on channel 13.
 (a)
(a)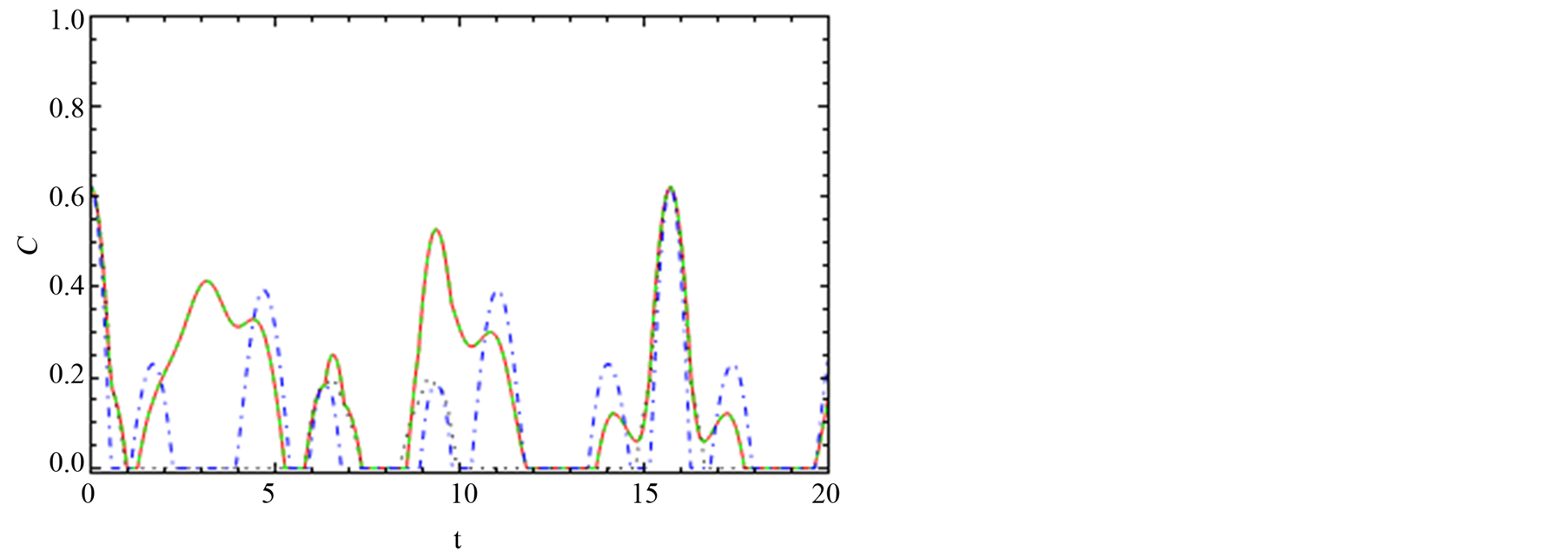 (b)
(b)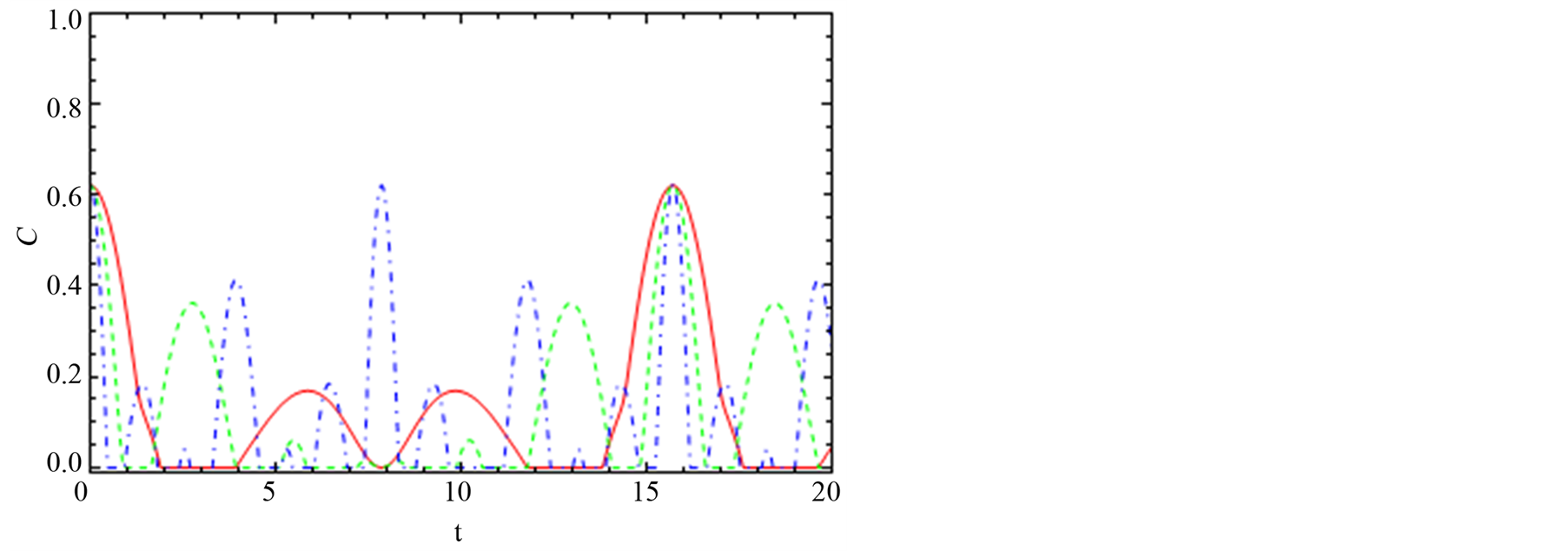 (c)
(c)
Figure 5. The dynamics of the entanglement, C12, between node “1” and node “2”. (a), (b) and (c) are the same with Figure 2 but the interaction switched on y-axis Dy = 0.2.
This figure shows the new feature is observed as the spin-orbit and the number of oscillations increased.
Figures 7(a)-(c) show the entanglement dynamics between node “1” and node “4”. In Figure 7(a), we see that the spin-orbit interaction contributes to the xand z-direction where the maximum value without the effect of the spin interaction is 4 × 1016 (solid red line), and with effect of the xand z-spin-orbit the entanglement reaches a maximum of 1 at t = 3.
The dotted green line shows no effect on the spin-orbit interaction in y-axis. Figure 7(b) is same as in Figure 6(b) but resides in channel “14” where the entanglement is not influenced by the spin-orbit in y-direction as one
 (a)
(a) (b)
(b)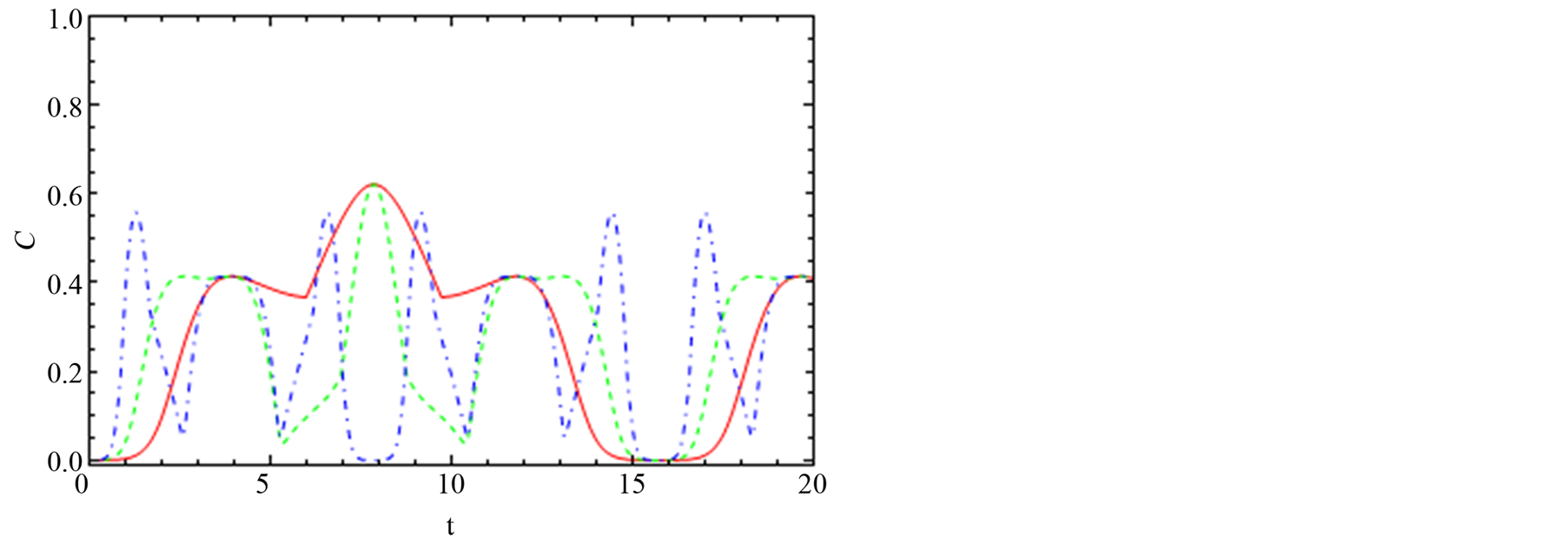 (c)
(c)
Figure 6. The dynamics of the entanglement, C13, between node “1” and node “3”. (a), (b) and (c) are the same with Figure 3 but the interaction switched on y-axis Dy = 0.2.
can see in the red and dashed green lines for Jx = Jy = 0.5 and Jy = Jz = 0.5, respectively. The dotted black line and dotted blue line are the combination of the spin-orbit interaction in xand z-direction which leads to the increasing in the entanglement oscillations. The effect of the spin-orbit affects the entanglement dynamics on channel “14” (see Figure 7(c)) where increasing the spin-orbit value leads to the number of oscillations increased.
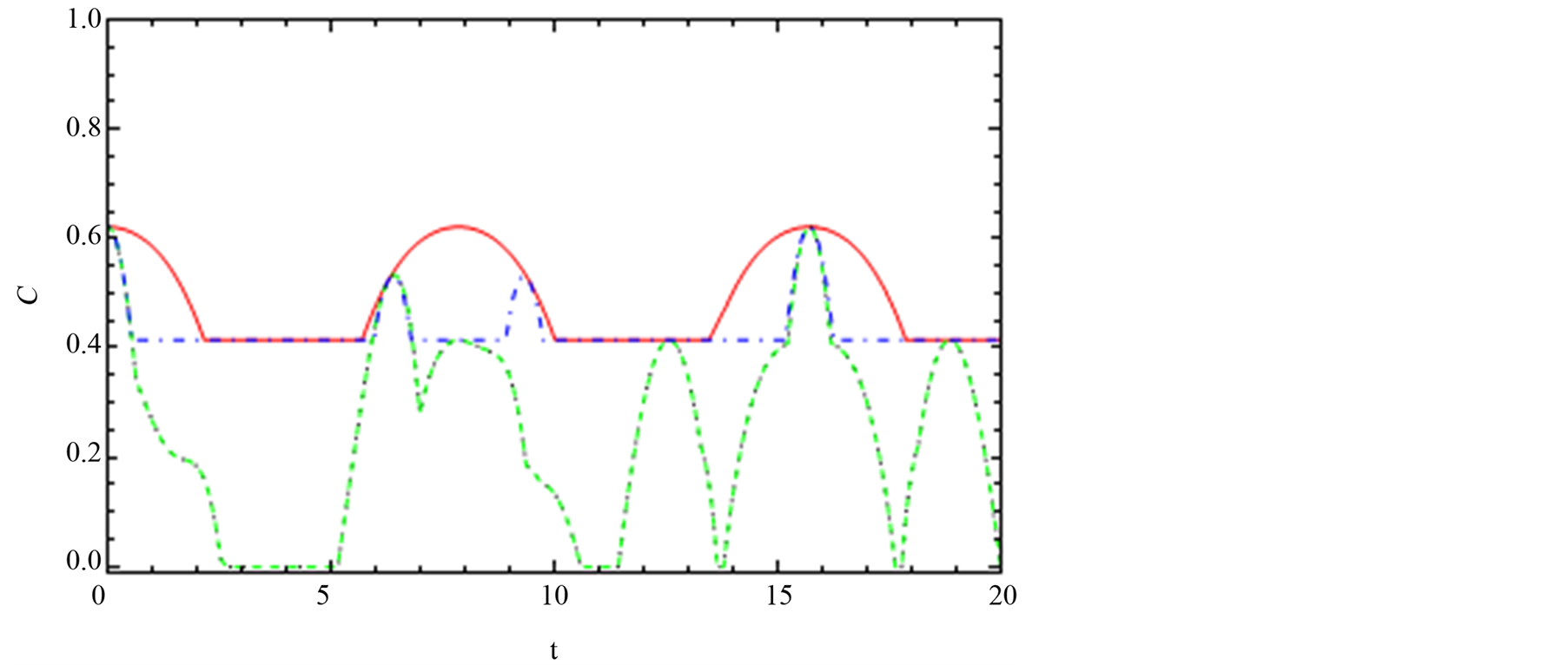
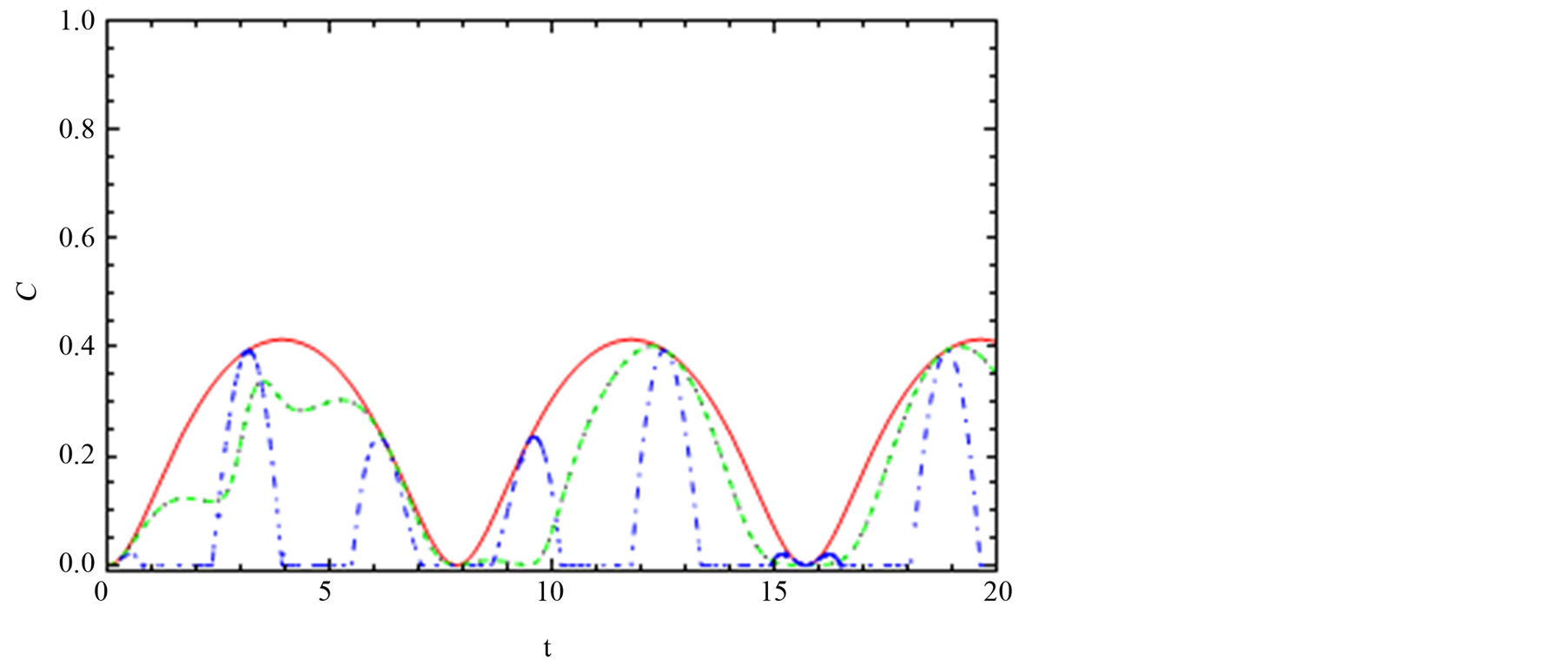
The effect of the spin-orbit interaction on the dynamics of the entanglement for the channel “12”, “13” and “14” with DM interaction is switched on the z-axis is depicted in Figures 8-10. Figure 8(a) shows the effect
 (a)
(a) (b)
(b)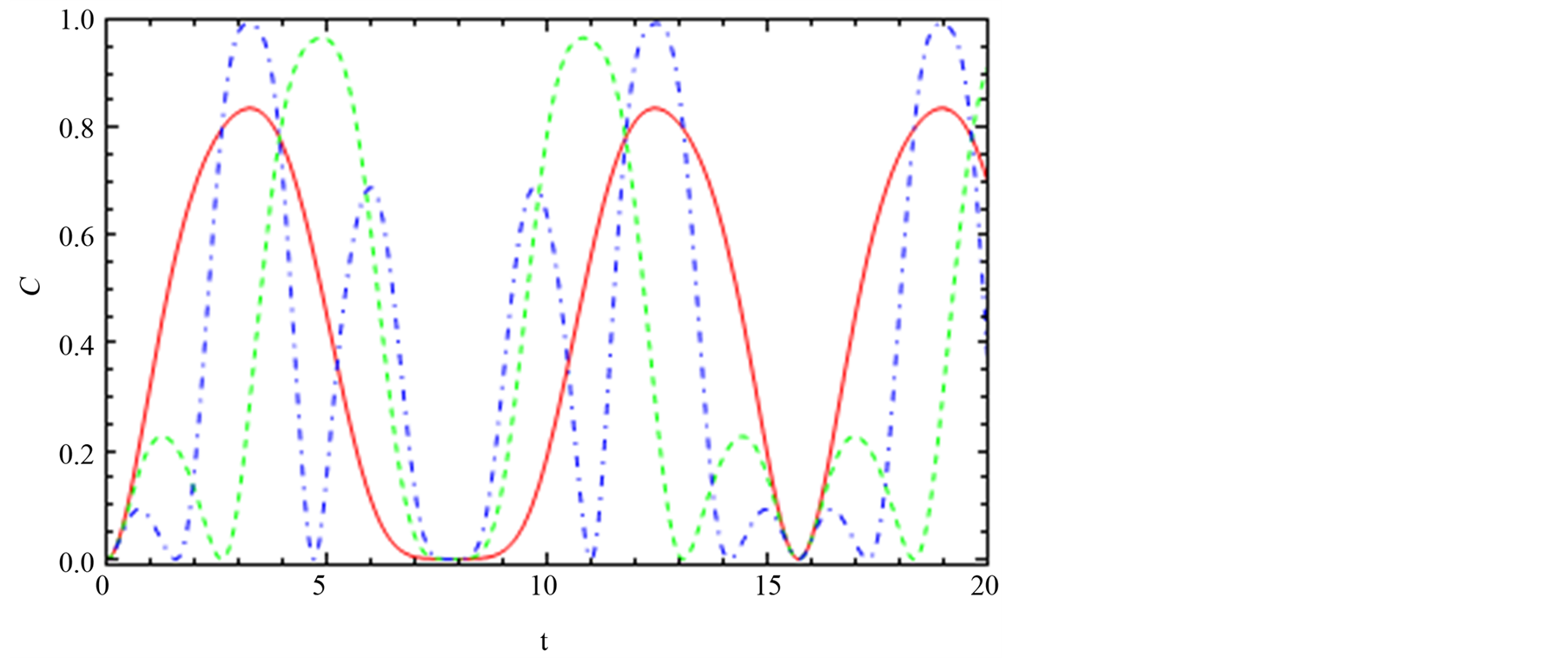 (c)
(c)
Figure 7. The dynamics of the entanglement, C14, between node “1” and node “4”. (a), (b) and (c) are the same feature with Figure 4 but the interaction switched on y-axis Dy = 0.2.
 (a)
(a)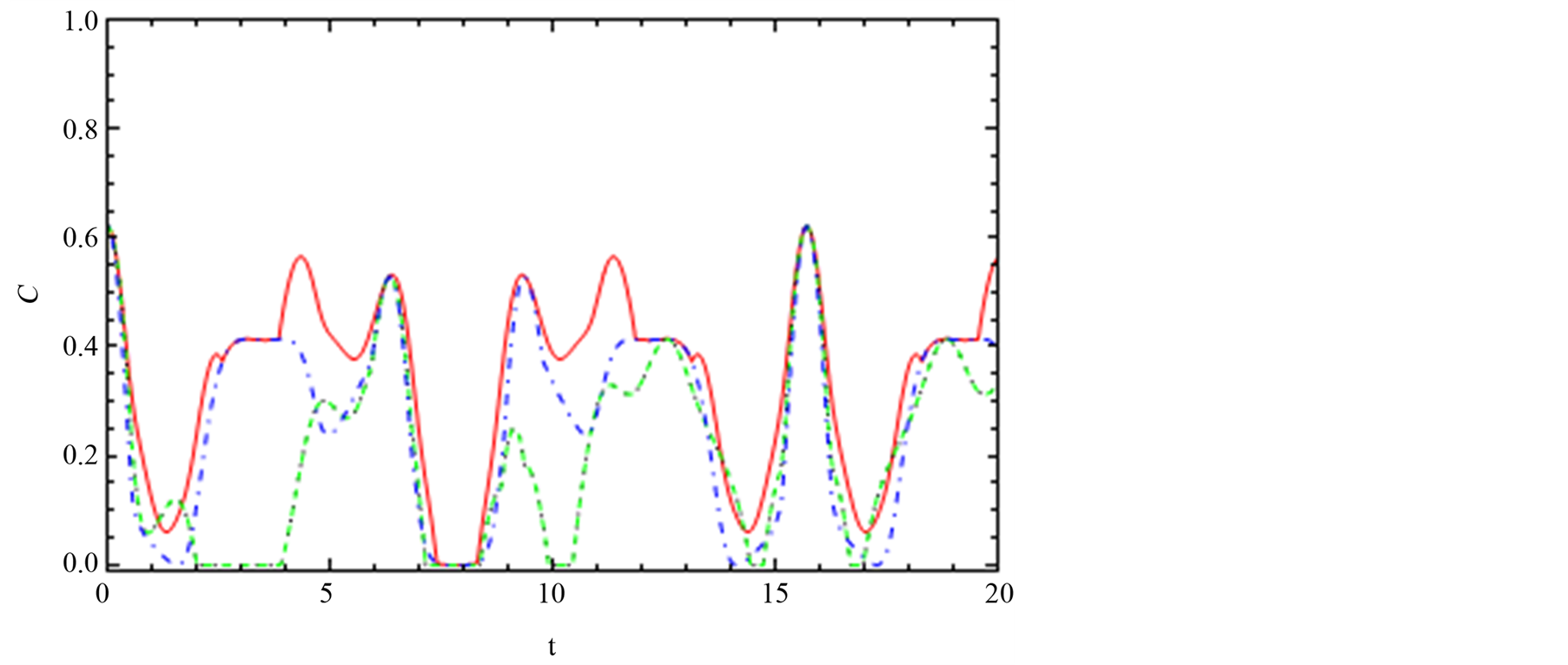 (b)
(b)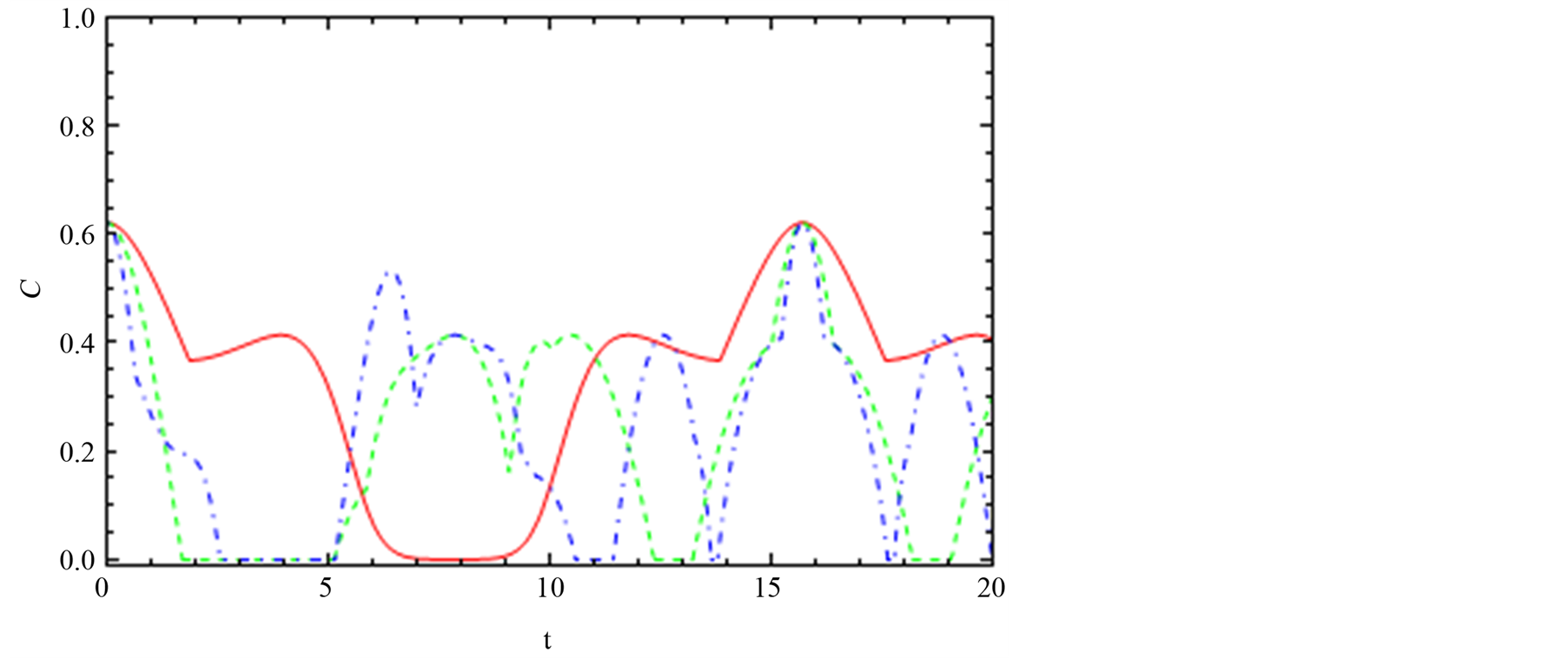 (c)
(c)
Figure 8. The dynamics of the entanglement, C12, between node “1” and node “2”. (a), (b) and (c) are the same feature with Figure 2 but the interaction switched on z-axis Dz = 0.2.
 (a)
(a) (b)
(b)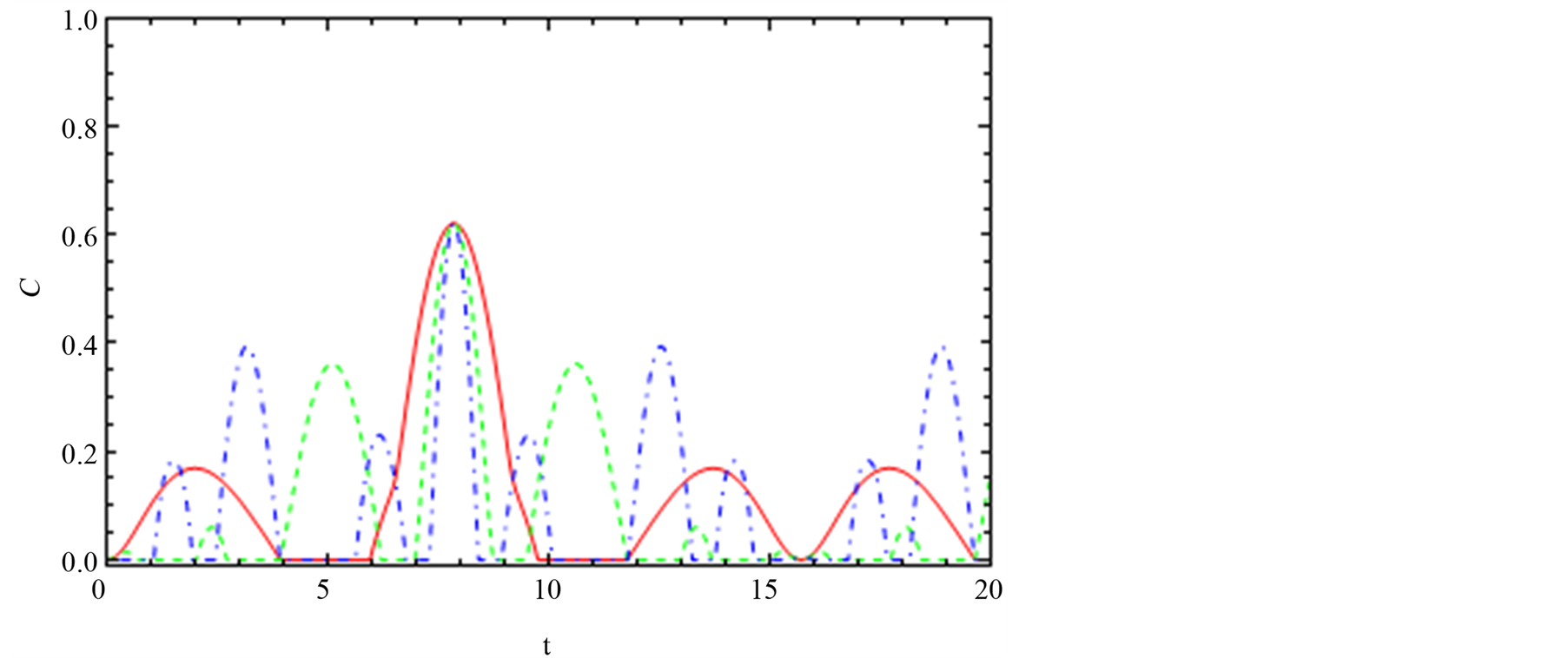 (c)
(c)
Figure 9. The dynamics of the entanglement, C13, between node “1” and node “3”. (a), (b) and (c) are the same with Figure 3 but the interaction switched on z-axis Dz = 0.2.
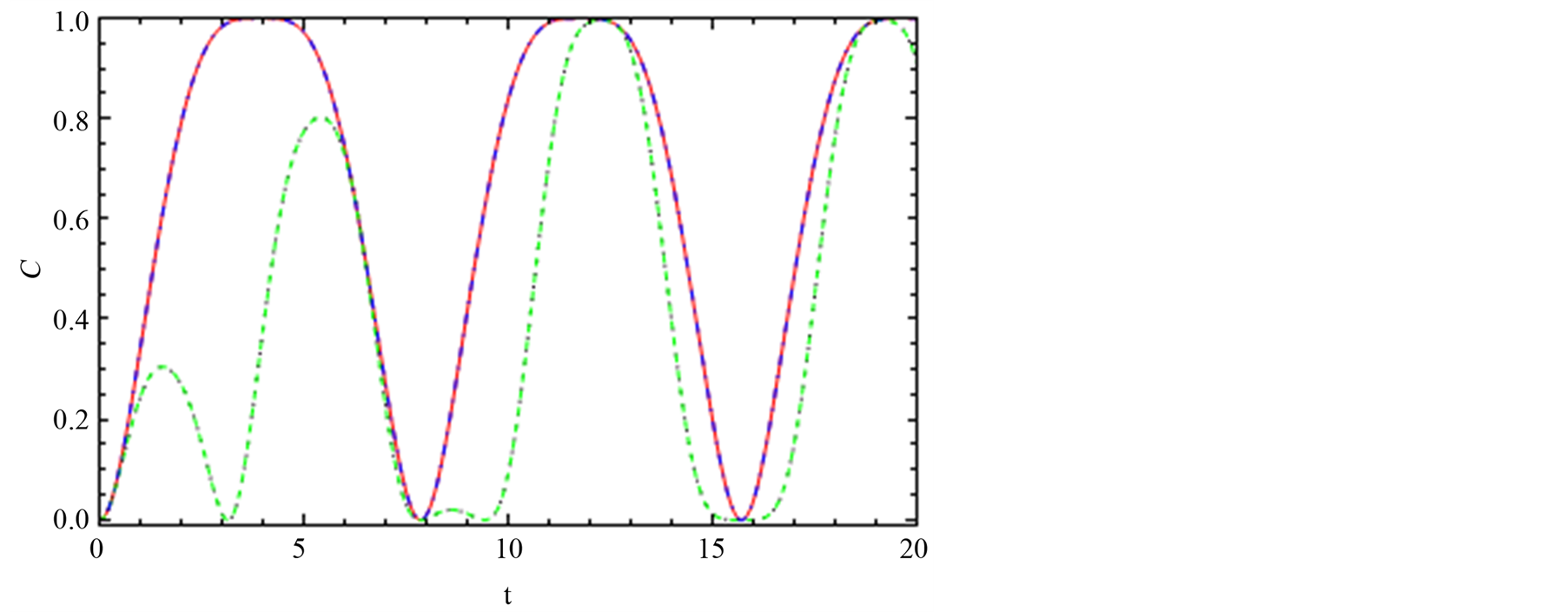 (a)
(a)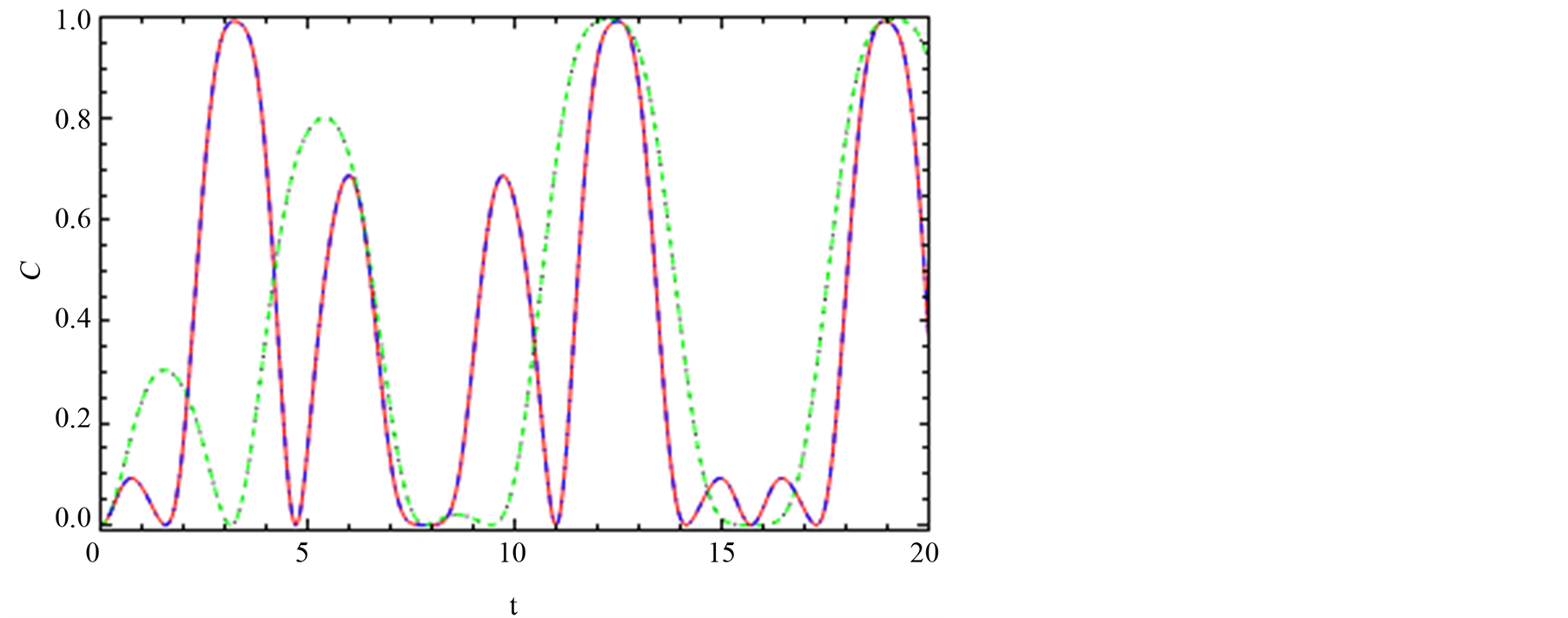 (b)
(b) (c)
(c)
Figure 10. The dynamics of the entanglement, C14, between node “1” and node “4”. (a), (b) and (c) are the same feature with Figure 4 but the interaction switched on y-axis Dz = 0.2.
of the spin-orbit interaction in one directional Jx, Jy and Jz. By comparison between Figure 8(a) and Figure 2(a), we find that the differences appeared on the effect of Jx in Figures 2-4 and Jz in Figures 8-10.
4. Conclusions
We discussed the effect of the spin-orbit (Heisenberg XYZ model) coupling to the entanglement between different nodes in the quantum network. It is shown that the entanglement decays for nonzero coupling. The phenomena of the entanglement sudden-death and sudden-birth appeared for larger coupling values. It shows that the coupling constant of the entangled channel initially has no effect on the upper bound of the entanglement. However, the lower bound of the entanglement does not vanish for non-zero couplings. The number of oscillations is increased as the coupling is increased. For entangled channels which are generated either via direct or indirect interactions, the concurrence and the number of oscillations are increased as the coupling is increased.
Finally, it is shown that the generated entangled channel between any two nodes via indirect interaction has a large degree of entanglement and the upper bound exceeds the initial entangled state. Therefore, one may generate maximum entangled state from the less entangled state by controlling the spin-orbit coupling. This means that terminals of the generated entangled network can be used to perform quantum information task with high efficiency.
References
- Chuang, I.L. and Nielsen, M.A. (2000) Quantum Computation and Quantum Information. Cambridge University Press, Cambridge.
- Prevedel, R., Walther, Ph., Tiefenbacher, F., Böhi, P.L., Kaltenbaek, R., Jennewein, Th. and Zeilinger, A. (2007) High-Speed Linear Optics Quantum Computing Using Active Feed-Forward. Nature, 445, 65-69.
- Gottesman, D. and Lo, H.-K. (2003) Proof of Security of Quantum Key Distribution with Two-Way Classical Communications. IEEE Transactions on Information Theory, 49, 457-475.
- Perseguers, S., Lapeyre Jr., G.J., Cavalcanti, D., Lewenstein, M. and Acín, A. (2013) Distribution of Entanglement in Large Scale Quantum Networks. Reports on Progress in Physics, 76, Article ID: 096001.
- Ahmed, A.-H.M., Cheong, L.Y., Zakaria, N. and Metwally, N. (2013) Dynamics of Information Coded in a Single Cooper Pair Box. International Journal of Theoretical Physics, 52, 1979-1988. http://dx.doi.org/10.1007/s10773-012-1399-9
- Weberruß, V.A. and Mahler, G. (1998) Quantum Networks. Springer, Berlin.
- Briegel, H.-J., Enk, S.J., Cirac, J.I., Zoller, P., Bouwmeeester, D., Pan, J.-W., Daniell, M., Weinfurter, H., Zeilinger, A., Vedral, V., Plenio, M.B. and Knight, P.L. (2000) Quantum Networks and Multi-Particle Entanglement. In: Bouwmeester, D., Ekert, A. and Zeilinger, A., Eds., The Physics of Quantum Information, Springer, Berlin Heidelberg 191-220.
- Gao, G. (2013) Cryptanalysis of a Multi-User Quantum Network System and Quantum Communication Using W-Type Entangled States. Journal of the Korean Physical Society, 62, 1093-1096. http://dx.doi.org/10.3938/jkps.62.1093
- Scheidl, Th., Wang, D., Kropatschek, S., Naylor, W., Wittmann, B., Mech, A., Kofler, J., Anisimova, E., Makarov, V., Jennewein, Th., Ursin, R., Zeilinger, A., Ma, X.-S. and Herbst, Th. (2012) Quantum Teleportation and Entanglement Distribution over 100-Kilometre Free-Space Channels. Nature, 489, 269-253.
- Laing, L.A. and O’Brien, J. L. (2012) Experimental Realization of Shor’s Quantum Factoring Algorithm Using Qubit Recycling. Nature Photonics, 6, 773-776. http://dx.doi.org/10.1038/nphoton.2012.259
- Elliott, Y.C. (2002) Building the Quantum Network. New Journal of Physics, 4, 46-53. http://dx.doi.org/10.1088/1367-2630/4/1/346
- Mink, A., Hershman, B.J., Nakassis, A., Tang, X., Lu, R., Su, D.H., Clark, C.W., Williams, C.J., Hagley, E.W., Wen, J., Bienfang, J. and Gross, A.J. (2004) Quantum Key Distribution with 1.25 gbps Clock Synchronization. Optics Express, 12, 2011-2016. http://dx.doi.org/10.1364/OPEX.12.002011
- Buntschu, F., Clausen, B., Felber, N., Gisin, N., Henzen, L., Junod, P., Litzistorf, G., Monbaron, P., Monat, L., Perroud, D., Ribordy, G., Rochas, A., Robyr, S., Tavares, J, Thew, R., Trinkler, P., Ventura, S., Voirol, R., Walenta, N., Stucki, D., Legr, M. and Zbinden, H. (2011) Long-Term Performance of the Swissquantum Quantum Key Distribution Network in a Field Environment. New Journal of Physics, 13, Article ID: 123001. http://dx.doi.org/10.1088/1367-2630/13/12/123001
- Ishizuka, H., Klaus, W., Wakui, K., Takeoka, M., Tanaka, A., Yoshino, K., Nambu, Y., Takahashi, S., Tajima, A., Tomita, A., Domeki, T., Hasegawa, T., Sakai, Y., Kobayashi, H., Asai, T., Shimizu, K., Tokura, T., Tsurumaru, T., Matsui, M., Honjo, T., Tamaki, K., Takesue, H., Tokura, Y., Dynes, J.F., Dixon, A.R., Sharpe, A.W., Yuan, Z.L., Shields, A.J., Uchikoga, S., Legre, M., Robyr, S., Trinkler, P., Monat, L., Page, J.-B., Ribordy, G., Poppe, A., Allacher, A., Maurhart, O., Langer, T., Peev, M., Zeilinger, A., Sasaki, M. and Fujiwara, M. (2011) Field Test of Quantum Key Distribution in the Tokyo QKD Network. Optics Express, 19, 10387-10409.
- Mtwallay, M. (2011) Entangled Network and Quantum Communications. Physics Letters A, 375, 4268. http://dx.doi.org/10.1016/j.physleta.2011.10.026
- Abdel-Aty, A.-H., Cheong, L.Y., Zakaria, N. and Metwally, N. (2013) Quantum Network via Partial Entangled State. The 3rd International Conference on Fundamental and Applied Sciences (ICFAS2014), Universiti Teknologi Petronas, Malaysia, (Accepted) to be appear in AIP Conference Proceedings.
- Abdel-Aty, A.-H., Cheong, L.Y., Zakaria, N. and Metwally, N. (2013) Entanglement and Teleportation via Partial Entangled-State Quantum Network. Quantum Information Processing (Submitted).
- Darwish, M., Obada, A.-S.F. and El-Barakaty, A. (2011) Purity Loss for a Cooper Pair Box Interacting Dispersively with a Nonclassical Field under Phase Damping. Applied Mathematics & Information Sciences, 5, 122.
- Abdel-Khalek, S. and Ahmed, A.M. (2011) Information Entropy of a Superconducting Charge Qubit Interacting with Two Cavity Fields. Applied Mathematics & Information Sciences, 5, 263S-273S.
- Moriya, T. (1960) New Mechanism of Anisotropic Superexchange Interaction. Physical Review Letters, 4, 228. http://dx.doi.org/10.1103/PhysRevLett.4.228
- Friesen, M., Chutia, S. and Joynt, R. (2006) Detection and Measurement of the Dzyaloshinskii-Moriya Interaction in Double Quantum Dot Systems. Physical Review B, 73, Article ID: 241304. http://dx.doi.org/10.1103/PhysRevB.73.241304
- Zhang, G.-F. (2007) Thermal Entanglement and Teleportation in a Two Qubit Heisenberg Chain with DzyaloshinskiMoriya Anisotropic Antisymmetric Interaction. Physical Review A, 75, Article ID: 034304. http://dx.doi.org/10.1103/PhysRevA.75.034304
- Li, S.-S., Ren, T.-Q., Kong, X.-M. and Liu, K. (2012) Thermal Entanglement in the Heisenberg (XXZ) Model with Dzyaloshinskiimoriya Interaction. Physica A, 391, 35-41.
- Yeo, Y. (2002) Teleportation via Thermally Entangled States of a Two-Qubit Heisenberg XX Chain. Physical Review A, 66, Article ID: 062312. http://dx.doi.org/10.1103/PhysRevA.66.062312
- Ye, M.-Y., Jiang, W., Chen, P.-X., Zhang, Y.-S., Zhou, Z.-W. and Guo, G.-C. (2007) Local Distinguishability of Orthogonal Quantum States and Generators of su(N). Physical Review A, 76, Article ID: 032329. http://dx.doi.org/10.1103/PhysRevA.76.032329
- Li, D.-C. and Cao, Z.-L. (2009) Thermal Entanglement in the Anisotropic Heisenberg (XYZ) Model with Different Inhomogeneous Magnetic Fields. Optics Communications, 282, 1226-1230. http://dx.doi.org/10.1016/j.optcom.2008.11.087
- He, Z., Xiong, Z. and Zhang, Y. (2006) Influence of Intrinsic Decoherence on Quantum Teleportation via Two-Qubit Heisenberg (XYZ) Chain. Physics Letters A, 354, 79-83. http://dx.doi.org/10.1016/j.physleta.2006.01.038
- Sharma, K.K., Awasthi, S.K. and Pandey, S.N. (2013) Entanglement Sudden Death and Birth in Qubitqutrit Systems under Dzyaloshinskiimoriya Interaction. Quantum Information Processing, 12, 3437-3447.
- Rafiee, M., Soltani, M., Mohammadi, H. and Mokhtari, H. (2011) Entanglement Transfer via xxz Heisenberg Chain with dm Interaction. The European Physical Journal D, 63, 473-482. http://dx.doi.org/10.1140/epjd/e2011-20032-5
- You, W.L. and Dong, Y.L. (2010) The Entanglement Dynamics of Interacting Qubits Embedded in a Spin Environment with Dzyaloshinsky-Moriya Term. The European Physical Journal D, 57, 439-445. http://dx.doi.org/10.1140/epjd/e2010-00056-1
- Obada, A.S.F. and Shaheen, M.E. (2013) Effect of the Thermal Photons on Fischr Information Dynamics for a Dispersive Jeans-Commings Model. Information Sciences Letters, 2, 165-171.
- Luo, S.S., Wang, M.M., Chen, X.B. and Yang, Y.X. (2012) Efficient Entanglement Channel Construction Schemes for a Theoretical Quantum Network Model with d Level System. Quantum Information Processing, 11, 1715-1739. http://dx.doi.org/10.1007/s11128-011-0325-z
- Majumdar, A.S., Adhikari, S., Ghosh, B., Nayak, N. and Roy, S. (2010) Teleportation via Maximally and Non-Maximally Entangled Mixed States. Quantum Information & Computation, 10, 398-419. http://dl.acm.org/citation.cfm?id=2011362.2011365
- Hill, S. and Wootters, W.K. (1997) Entanglement of a Pair of Quantum Bits. Physical Review Letters, 78, 5022-5025. http://dx.doi.org/10.1103/PhysRevLett.78.5022

