Journal of Quantum Information Science
Vol.2 No.2(2012), Article ID:20127,8 pages DOI:10.4236/jqis.2012.22004
Entanglement Generation in Spatially Separated Systems Using Quantum Walk
1Optics & Quantum Information Group, the Institute of Mathematical Sciences, Chennai, India
2Department of Physics, University College Cork, Cork, Republic of Ireland
3Indian Institute of Technology, Jodhpur, India
Email: *cmadaiah@phys.ucc.ie, goyal@imsc.res.in, subhashish@iitj.ac.in
Received January 20, 2012; revised March 9, 2012; accepted March 30, 2012
Keywords: Quantum Walk; Entanglement Generation; Localization
ABSTRACT
We present a scheme for generating entanglement between two spatially separated systems from the spatial entanglement generated by the interference effect during the evolution of a single-particle quantum walk. Any two systems which can interact with the spatial modes entangled during the walk evolution can be entangled using this scheme. A notable feature is the ability to control the quantum walk dynamics and its localization at desired pair lattice sites irrespective of separation distance resulting in a substantial control and improvement in the entanglement output. Implementation schemes to entangle spatially separated atoms using quantum walk on a single atom is also presented.
1. Introduction
Entanglement is an indispensable resource for performing various quantum tasks (see [1] for a recent review, [2] and reference therein for entanglement preparation). Several schemes have been proposed [3-6] for the generation and distribution of entanglement between different systems, most of which involve an initial entangling of the two systems followed by spatial separation. Such spatially separated and entangled states can be used for quantum communication protocols, for example, quantum cryptography [7] and quantum teleportation [8]. Amount of entanglement degrades with increase in spatial separation because of physical limitations and noise effect. One way of circumventing this problem would be to generate entanglement when the two systems are spatially separated.
In this article, we present a new scheme to efficiently generate entanglement between two spatially separated systems from a single particle system [9]. It has been shown by two of the present authors that a quantum walks evolution of a particle in a one-dimensional lattice results in the entanglement of the lattice sites after a sufficient number of walk steps [10]. Although this spatial entanglement by itself does not have much physical significance, we nevertheless make use of it in entangling two initially unentangled systems that are spatially separated. Direct control over the quantum coin operation makes it possible to control the dynamics of the evolution of the quantum walk [11,12] which in turn allows us to optimize the entanglement output. The ability to localize the evolution at different lattice sites simultaneously, a novel phenomenon which has been discussed for the first time in this article, leads to a substantial improvement in the entanglement generated. This is a generic scheme that can be implemented to entangle any two systems that interact with the modes entangled due to quantum walk. Experimental implementation of quantum walk has been reported with samples in nuclear magnetic resonance (NMR) systems [13-15]; in the form of optical Galton board [16] and quantum quincunx [17]; in the continuous tunneling of light fields through waveguide lattices [18]; in the phase space of trapped ions [19, 20]; with single optically trapped atoms [21]; and with single photon [22,23]. There are various other schemes proposed to implement quantum walk in other systems [24-26]. Using our scheme, all these systems have the potential to generate entanglement between two spatially separated, uncorrelated systems.
This article is arranged as follows. In Section 2 we describe a toy model which has the basic ingredients of our proposal: 1) two entangled modes are generated and distributed to the distant locations of two uncorrelated systems A and B; 2) the entanglement of these modes is then transferred to A and B via some interaction. In Section 3 we describe the discrete-time quantum walk model and the entanglement between its spatial degrees of freedom. Section 4 discusses how to use this spatial entanglement to entangle two uncorrelated, spatially separated systems A and B. The Hamiltonian modelling the interaction of these systems with the lattice sites is motivated by two examples: quantum walk with single photons and quantum walk in a spin chain; in both cases A and B are taken to be two-level systems. In Section 5 we explain how to localize the quantum walk distribution around desired lattice sites, in such a way that the entanglement between these sites is maximized. We then show how this affects the entanglement transferred to systems A and B. In Section 6 we propose experimental implementtations of our proposal to entangle two uncorrelated atoms in an optical lattice. We conclude in Section 7.
2. Toy Model
Before proceeding to our scheme, we will introduce the basic idea using a simple model involving a beam splitter, a photon, and two two-level atoms. The aim is to generate entanglement between the uncorrelated atoms, labeled by A and B, which are placed in distant locations (see Figure 1). First, a photon in the initial state  is passed through the beam splitter. The state of the photon passing through the beam splitter are spatially separated into the horizontal(h) and vertical(v) modes and it can be written as
is passed through the beam splitter. The state of the photon passing through the beam splitter are spatially separated into the horizontal(h) and vertical(v) modes and it can be written as
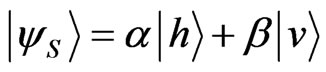 (1)
(1)
such that , where
, where 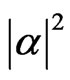 and
and 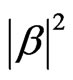 represent the probability of finding the photon in the h and v modes, respectively. For convenience, we can rewrite the state of the photonic modes in terms of the number of photons in each polarization mode:
represent the probability of finding the photon in the h and v modes, respectively. For convenience, we can rewrite the state of the photonic modes in terms of the number of photons in each polarization mode:
 . (2)
. (2)
The state 
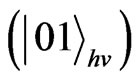 represents one photon in the h(v) mode and no photon in v(h) mode. This state is entangled unless α or β is zero. This entanglement between the polarization modes can be used to entangle A and B. This is done by placing atoms A and B initially in the ground state
represents one photon in the h(v) mode and no photon in v(h) mode. This state is entangled unless α or β is zero. This entanglement between the polarization modes can be used to entangle A and B. This is done by placing atoms A and B initially in the ground state 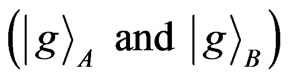 at the two exit points of the photon coming from the beam splitter. The conditions are such that if the photon is in v(h) mode, atom A(B) will get excited, that is,
at the two exit points of the photon coming from the beam splitter. The conditions are such that if the photon is in v(h) mode, atom A(B) will get excited, that is,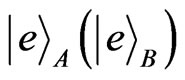 . The final collective state of these two atoms can be written as:
. The final collective state of these two atoms can be written as:
 . (3)
. (3)
This provides a very simple model of generating entanglement between two distant systems from the entanglement between the photonic modes. Its pictorial representation is as in Figure 1. As we commented at the end of the Introduction, the new scheme we propose below has the ingredients of the preceding toy model; which we now describe.
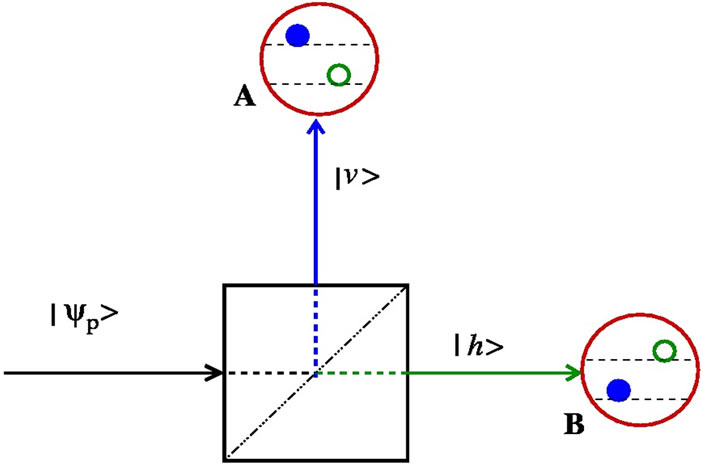
Figure 1. Photon in state when  passed through the beam splitter gets separated making h and v modes which are entangled. Two, initially uncorrelated, two-level atoms (A and B) in ground state can be entangled by interacting them with the two modes separately.
passed through the beam splitter gets separated making h and v modes which are entangled. Two, initially uncorrelated, two-level atoms (A and B) in ground state can be entangled by interacting them with the two modes separately.
3. Spatial Entanglement Using Single-Particle Quantum Walk
Discrete-time quantum walk is defined on a coin Hilbert space Ηc and position Hilbert space ΗP. In one dimension, Ηc is spanned by the basis states 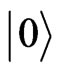 and
and  and ΗP. is spanned by the basis state
and ΗP. is spanned by the basis state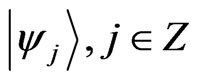 . Each step of the quantum walk on a particle initially in superposition of the coin states at origin (j = 0) given by,
. Each step of the quantum walk on a particle initially in superposition of the coin states at origin (j = 0) given by,
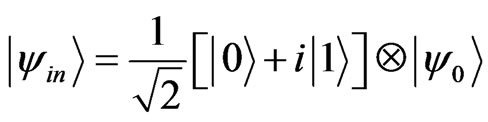 (4)
(4)
is implemented by applying a conditional shift operation S followed by the quantum coin operation C. The operation S can be defined such that the state 
 moves to the left (right),
moves to the left (right),
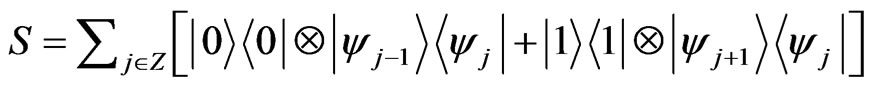 . (5)
. (5)
The operation C follows the operation S and evolves the coin basis states [11,27,28]. It was shown in [12] that complete control over the dynamics of the walk can state at the new position into a superposition of the be accomplished by choosing C as a three parameter SU(2) group element; here, however, we take, for simplicity, the widely used Hadamard operator, that is,
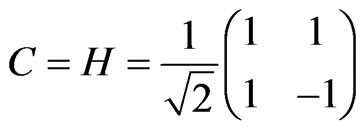 , (6)
, (6)
which is an element of U(2) group. In order to show the analytics of spatial entanglement, we consider only three steps of the walk, after which the state of the particle can be written as:
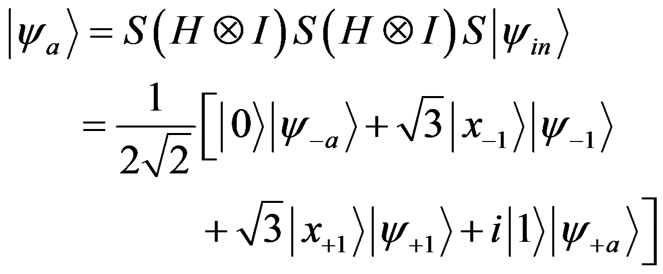 (7)
(7)
where

and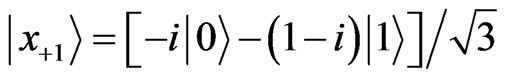 . Let us concentrate on the lattice sites −1 and +1 only, and denote its position states as
. Let us concentrate on the lattice sites −1 and +1 only, and denote its position states as 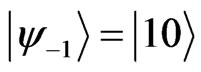 and
and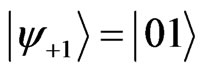 . The reduced density matrix, after tracing out the other lattice sites and the coin degrees of freedom, is:
. The reduced density matrix, after tracing out the other lattice sites and the coin degrees of freedom, is:
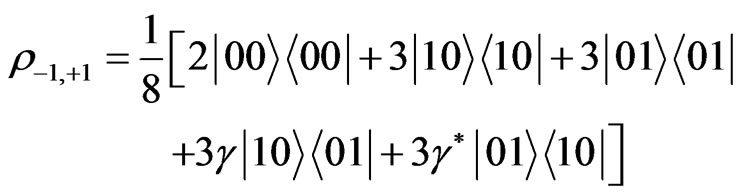 (8)
(8)
where  and
and 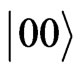 refers to the state when the walker is neither in the +1 nor in the −1 site. The partial transpose of the above matrix will always be nonpositive. Therefore, the reduced density matrix
refers to the state when the walker is neither in the +1 nor in the −1 site. The partial transpose of the above matrix will always be nonpositive. Therefore, the reduced density matrix 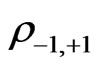 represents an entangled state showing that the lattice sites −1 and +1 are entangled (cf. [29]). The next task is to use this spatial entanglement to generate entanglement between two uncorrelated systems which we will call A and B in the following.
represents an entangled state showing that the lattice sites −1 and +1 are entangled (cf. [29]). The next task is to use this spatial entanglement to generate entanglement between two uncorrelated systems which we will call A and B in the following.
4. Generation of Entanglement between Two Spatially Separated Systems from Spatially Entangles Modes
It was shown some years ago that two distant spins A and B become entangled after interacting with the spins of an entangled pair through a beam-splitter-like Hamiltonians [30]. The protocol, we propose, to generate entanglement between systems A and B is to: (1) evolve the desired number of quantum walk steps on a particle in lattice to generate entanglement between two spatial modes without having A and B interacting with the lattice, and (2) stop the quantum walk evolution and switch on the interaction between A and B at the desired lattice sites which are spatially entangled. The interaction of systems A and B with the entangled lattice sites depends upon the nature of the system, on which quantum walk is being performed and the properties of the system A and B. In this section, we will consider entangling two distant spins, fermions using quantum walk on a one-dimensional lattice consisting of spin-1/2 particles and this can be extended to bosonic system as shown in Section 6.
For a spin-1/2 system, the spin hops from one lattice site to another in a quantum walk evolution. By using Jordon-Wigner transformation [31] a spin-1/2 system can be mapped to a spinless fermionic system. Therefore, a one-dimensional spin-1/2 lattice with all spins but one, pointing downward can be viewed as a system consisting of a single spinless fermion. By attaching an extra coin degree of freedom with the fermion one can perform quantum walk. Now if systems A and B are also spin-1/2 particles, spanned by the basis  interacting with the spins at ±l lattice sites, the interaction Hamiltonian can be written as
interacting with the spins at ±l lattice sites, the interaction Hamiltonian can be written as
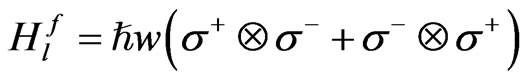 . (9)
. (9)
In the preceding Hamiltonian, 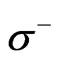 and
and 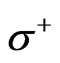 stands for the lowering,
stands for the lowering, 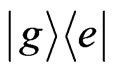 and raising,
and raising,  operator for spin respectively. After letting A interact with spatial mode of spin at –l and B with spatial mode of spin at –l for time t given by the evolution operator
operator for spin respectively. After letting A interact with spatial mode of spin at –l and B with spatial mode of spin at –l for time t given by the evolution operator
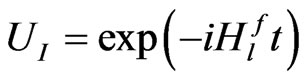 , (10)
, (10)
and the state of the system AB can be written as:
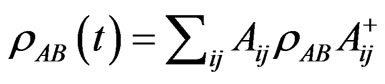 . (11)
. (11)
Here 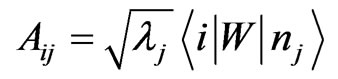 are Kraus operators and:
are Kraus operators and:
 is an orthonormal basis in
is an orthonormal basis in 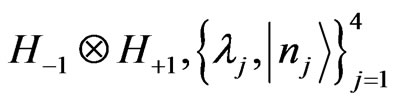
forms the set of eigenvalues and eigenvectors for 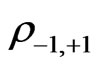 and ρAB is the initial state of the system AB. The unitary operator W, responsible for the joint evolution is:
and ρAB is the initial state of the system AB. The unitary operator W, responsible for the joint evolution is:
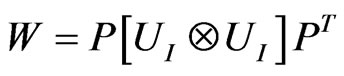 (12)
(12)
where P is a permutation operator such that
 . (13)
. (13)
More detailed description of the process of transferring the entanglement in spin system can be seen in Ref. [32] where quantum walk has been used for state transfer in a spin system.
In Figure 2, we show the evolution of entanglement between systems and for different initial states, using concurrence [33] as the measure. Following the previous section, we have considered the interaction of and with the −1 and +1 lattice sites, respectively, after three steps of the walk. We observe that the amount of entanglement depends on the initial state of the system and different

Figure 2. The evolution of generated entanglement between A and B, spanned by the basis 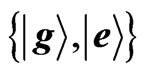 with different initial states under the influence of interaction with entangled lattice sites ±1 after three step of quantum walk. (a)
with different initial states under the influence of interaction with entangled lattice sites ±1 after three step of quantum walk. (a)
 , (b)
, (b)  and (c)
and (c)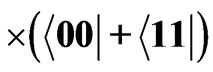
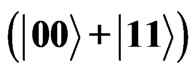
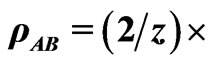 .
.
separable states achieve maxi-mum entanglement at the same time.
5. Localization of Quantum Walk at Different Lattice Sites
The degree of spatial entanglement between two lattice sites depends largely on two points [10]: 1) the degree of interference during the quantum walk, and 2) the value of the probability amplitude at the particular lattice sites. Both of these can be achieved by evolving and localizing the quantum walk around the desired lattice sites with some degree of interference. To further understand the contribution of localization of quantum walk to increase the degree of spatial entanglement, we will consider the lattice state after t steps of quantum walk that can be written as
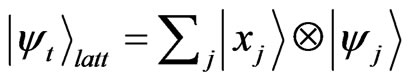 , (14)
, (14)
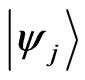 represents a state where lattice site j is occupied with other sites being empty and
represents a state where lattice site j is occupied with other sites being empty and 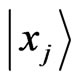 represents the corresponding coin state. Let us say we are interested in particular lattice sites ±l. Then in the reduced density matrix
represents the corresponding coin state. Let us say we are interested in particular lattice sites ±l. Then in the reduced density matrix  which is of the form given by Equation (8), with off diagonal terms
which is of the form given by Equation (8), with off diagonal terms 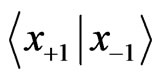 and diagonal terms depending on the amplitude of all
and diagonal terms depending on the amplitude of all  states, the states other than
states, the states other than 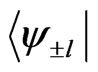 will also contribute to
will also contribute to 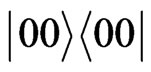 If the amplitude of all the
If the amplitude of all the 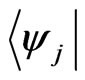 states except for
states except for 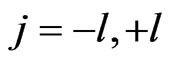 is zero then the coefficient of
is zero then the coefficient of  will be zero resulting in the maximum value of
will be zero resulting in the maximum value of  which contributes for spatial entanglement. Therefore, in localized states, that is, the states in which the amplitude is localized in a very narrow lattice space, the coefficient of
which contributes for spatial entanglement. Therefore, in localized states, that is, the states in which the amplitude is localized in a very narrow lattice space, the coefficient of 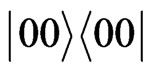 will be very small resulting in maximizing
will be very small resulting in maximizing 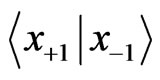 and hence the amount of spatial entanglement will be more.
and hence the amount of spatial entanglement will be more.
To realize this using quantum walk, we will begin by generalizing the previous discussions on quantum walk evolution by taking a more general coin operator
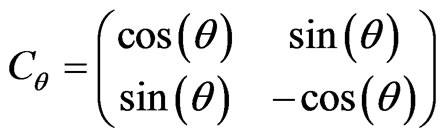 . (15)
. (15)
During the walk evolution, if θ = 0 the amplitude of the two basis states move away from each other and for θ = π/2 the amplitude shifts between the origin (j = 0) and its neighboring positions (±1). In both these cases the walk evolves without resulting in any interference [12]. Even for θ close to 0 and π/2 the interference effect will be very small resulting in very small or zero spatial entanglement. When θ = π/24 the walk evolves with good degree of interference but with a spread of the amplitudes in position space (asymptotically, the distribution is homogeneous) resulting in a very low amplitude for lattice sites ±l far away from each other. Therefore, to maximize the amount of spatial entanglement between lattice sites irrespective of the separation distance, one needs to control the quantum walk evolution in such a way that its amplitude is localized, with a good degree of interference for any lattice site separation distance.
Localization of quantum walk at the origin has been discussed in Refs. [34-38]. Here, we briefly discuss a way to localize the walk around the desired lattice sites such that, it is scalable for site ±l far away from each other. This can be done by first delocalizing the walk to sites ±l with minimum interference resulting in large 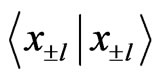 and very small
and very small  followed by localization around sites ±l to improve
followed by localization around sites ±l to improve  at the cost of
at the cost of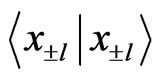 . As discussed earlier, choosing θ very close to zero will result in two peaks at lattice sites ±l = ±tcos(θ) moving away from each other with minimal interference, where t is the number of steps of the walk [12]. Therefore, even for very large t steps, of walk delocalize at ±l position with very small
. As discussed earlier, choosing θ very close to zero will result in two peaks at lattice sites ±l = ±tcos(θ) moving away from each other with minimal interference, where t is the number of steps of the walk [12]. Therefore, even for very large t steps, of walk delocalize at ±l position with very small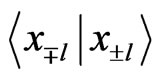 . In Ref. [36] it was shown that choosing a value of θ randomly picked from the interval {π/4, π/2} at each step of the walk, localizes the quantum walk distribution around the initial position and the localization is a result of interference. Therefore, choosing θ randomly from the interval {π/4, π/2} for each step of the after the walk is delocalized at ±l results in some improvement of
. In Ref. [36] it was shown that choosing a value of θ randomly picked from the interval {π/4, π/2} at each step of the walk, localizes the quantum walk distribution around the initial position and the localization is a result of interference. Therefore, choosing θ randomly from the interval {π/4, π/2} for each step of the after the walk is delocalized at ±l results in some improvement of  at the cost of
at the cost of  which in turn contributes for spatial entanglement.
which in turn contributes for spatial entanglement.
Figure 3, shows the localization of the amplitudes at positions −95 and +95 after 100 and 200 steps of the walk; for the first 95 steps we choose θ ≈ π/36 followed by θ Î{π/4, π/2} for remaining steps. Note that the peaks do not move away even after 200 steps of the walk. This protocol for localization at desired sites will hold even for a very large spatial separation of lattice sites making it scalable. One should avoid using θ = 0 during the first part of the evolution, because as commented above, the walk, in this case, evolves without interference. As for the entanglement transferred to the uncorrelated systems A and B (see the previous section), in Figure 4, we show the evolution of their concurrence when they interact with lattice sites ±95 after 200 steps of the walk. Although the amount of entanglement in this case is smaller than that of Figure 2, qualitatively both evolutions are identical. The decrease in amount of entanglement is mainly due to the delocalization and localization of the walk which was not required for a 3-step walk used to obtain Figure 2.
6. Implementation Scheme in a Physical System
Until last year, very few experimental implementations of discrete-time quantum walk [14,16,17] were reported.
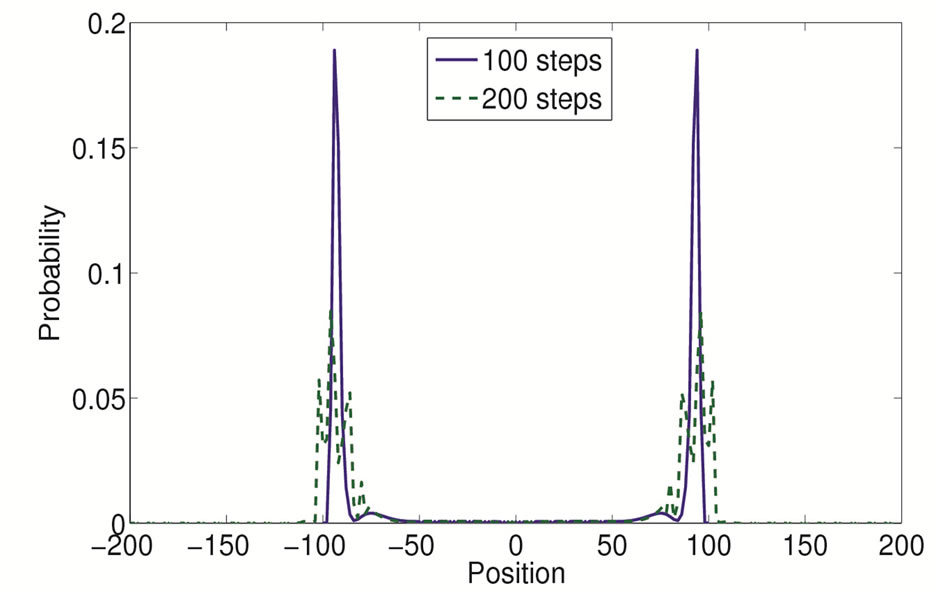
Figure 3. Localization of quantum walk around lattice sites ±95. Localization contributes to the increase in the degree of spatial entanglement which can be used to entangle two spatially separated uncorrelated systems.
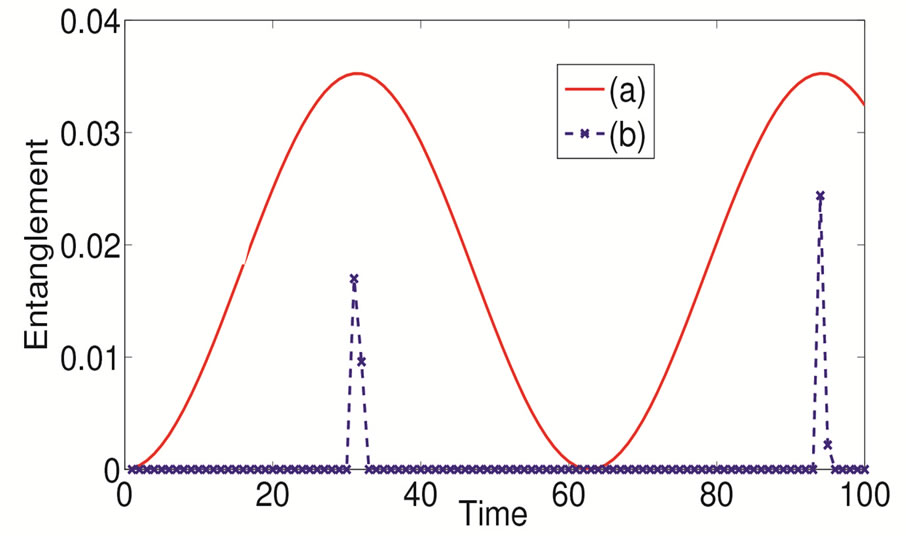
Figure 4. The evolution of generated entanglement between A and B with different initial states under the influence of interaction with entangled lattice sites ±95. Entanglement was generated after the walk was localized at site ±95. (a)  and (b)
and (b) .
.
However, in the last one year, many implementations of few steps of discrete-time quantum walk at single particle level, using trapped ions [19,20]; with optically trapped atoms [21]; and with photons [22,23] have been achieved. Along with experimental implementation, precise levels of control over the single particle quantum walk evolution by controlling the quantum coin parameters have been demonstrated. These developments suggest that our scheme is directly implementable in the presently available quantum walk setups. Among the experimental setups mentioned above, we discuss a couple of them: quantum walk with atoms and photons, in detail. For bosonic systems like atoms and photon, the interaction Hamiltonian is:
 , (16)
, (16)
where 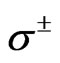 are the spin raising and lowering operators and
are the spin raising and lowering operators and  are the creation and annihilation operators, respectively. Using the time evolution operator
are the creation and annihilation operators, respectively. Using the time evolution operator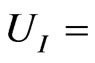 ,
, 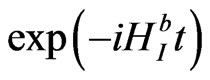 atoms A and B can be entangled as discussed for the case of the spin system.
atoms A and B can be entangled as discussed for the case of the spin system.
6.1. Entangling Atoms A and B from Spatial Modes of Quantum Walk with Atom
In a recent experimental implementation of discrete-time quantum walk using neutral atoms, single laser cooled Cesium (Cs) atoms were deterministically delocalized over the sites of a one-dimensional spin-dependent optical lattice [21]. Initially, the atoms distributed among the axial vibrational state were prepared in the 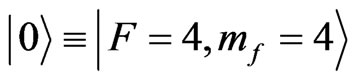 hyperfine state by optical pumping, where F is the total angular momentum, and mf its projection onto the quantization axis along the dipole trap axis. A resonant microwave radiation, consisting of a π/2 pulse was used to coherently couples this state to the
hyperfine state by optical pumping, where F is the total angular momentum, and mf its projection onto the quantization axis along the dipole trap axis. A resonant microwave radiation, consisting of a π/2 pulse was used to coherently couples this state to the 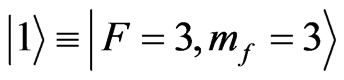 state and initialize the system in the superposition,
state and initialize the system in the superposition,  that is,
that is,
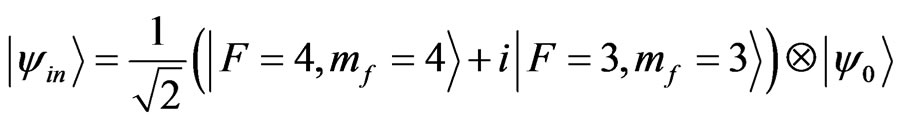 .(17)
.(17)
The state-dependent shift operation (S) is performed by continuous control of the trap polarization, moving the spin state 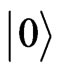 to the left and state
to the left and state 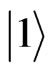 to the right adiabatically along the lattice axis. After t steps of the quantum walk, that is, a coin operation consisting of a (π/2) pulse and a state-dependent shift operation (S), the final atomic distribution is probed by fluorescence imaging. From these images, the exact lattice site of the atom after the walk is extracted and compared to the initial position of the atom. The final probability distribution to find an atom at position x after t steps is obtained from the distance each atom has walked by taking the ensemble average over several hundreds of identical realizations of the sequence.
to the right adiabatically along the lattice axis. After t steps of the quantum walk, that is, a coin operation consisting of a (π/2) pulse and a state-dependent shift operation (S), the final atomic distribution is probed by fluorescence imaging. From these images, the exact lattice site of the atom after the walk is extracted and compared to the initial position of the atom. The final probability distribution to find an atom at position x after t steps is obtained from the distance each atom has walked by taking the ensemble average over several hundreds of identical realizations of the sequence.
Experimental complexity aside, the preceding protocol can be adapted to other species of ultracold atoms. For example, in Rubidium (87Rb) atoms in an optical trap, states  and
and 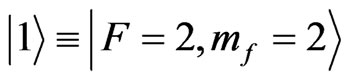 can be coherently coupled to implement quantum walk. To observe localization at a desired lattice site as discussed in Section 5, a π/2 pulse used as quantum coin operation during each step of the walk in the preceding protocols is replaced by a pulse with a very small value followed by a pulse randomly picked from the range {π/4, π/2}. The above evolution will direct the constructive interference towards the desired lattice sites.
can be coherently coupled to implement quantum walk. To observe localization at a desired lattice site as discussed in Section 5, a π/2 pulse used as quantum coin operation during each step of the walk in the preceding protocols is replaced by a pulse with a very small value followed by a pulse randomly picked from the range {π/4, π/2}. The above evolution will direct the constructive interference towards the desired lattice sites.
Once the walk is localized, the optical lattice on which the walk is implemented is made to overlap with another optical lattice on which the spatially separated atoms, to be entangled, are placed. After overlapping the two lattices, radio frequency pulses can be used to couple states in the different lattices [39] and entangle atoms A and B. In Figure 5, we have shown the schematic picture of the setup. In many schemes referred in [39], to entangle two atoms, A and B which cannot have any direct interaction between each other, they have to be made to interact via interaction Hamiltonian with two other entangled atoms. In our scheme, all we need is a single atoms in optical lattice and we can generate entanglement between two uncorrelated atoms in other system.
6.2. Entangling Atoms from Spatial Modes of Quantum Walk with Photon
All three implementations of discrete-time quantum walk on photons [18,22,23] known till date can be conveniently used to localize the quantum walk at the desired lattice site and entangle spatially separated, non-interacting atoms in an optical lattice. We consider a particular implementation using a single photon [23] to illustrate this further. A single photon created via parametric down conversion was initialized to a state of left-circular polarization,
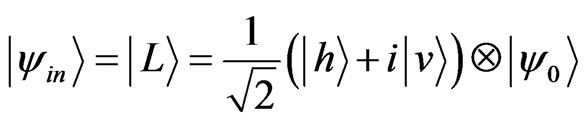 (18)
(18)
where  and
and 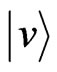 are horizontal and vertical polarization modes. Initialization leading to symmetric superposition state, as in Equation (4), was done using a quarterand a half-wave plate. Shift operator (S) was realized using birefringent calcite beam displacer and the coin operations used were Hadamard operation H, realized using half-wave plate with axis at π/8 to the polarization plane. The above setup can be modified to localize the quantum walk at a desired lattice site by replacing the Hadamard coin operation by a more general coin operation of the form Cθ discussed in Section 5. The coin operation Cθ to localize the walk can be realized using a half-wave plate with axis at θ/2 to the polarization plane. Once the walk is configured to localize at desired positions, the output can be directed towards spatially separated, non-interacting atoms in the optical lattice. When the photon on which the quantum walk is implemented is carefully chosen to match the transition energy level of atoms, spatially delocalized photons are absorbed by spatially separated atoms and generate entanglement between the “Equation (16)”. In this paper we have only
are horizontal and vertical polarization modes. Initialization leading to symmetric superposition state, as in Equation (4), was done using a quarterand a half-wave plate. Shift operator (S) was realized using birefringent calcite beam displacer and the coin operations used were Hadamard operation H, realized using half-wave plate with axis at π/8 to the polarization plane. The above setup can be modified to localize the quantum walk at a desired lattice site by replacing the Hadamard coin operation by a more general coin operation of the form Cθ discussed in Section 5. The coin operation Cθ to localize the walk can be realized using a half-wave plate with axis at θ/2 to the polarization plane. Once the walk is configured to localize at desired positions, the output can be directed towards spatially separated, non-interacting atoms in the optical lattice. When the photon on which the quantum walk is implemented is carefully chosen to match the transition energy level of atoms, spatially delocalized photons are absorbed by spatially separated atoms and generate entanglement between the “Equation (16)”. In this paper we have only
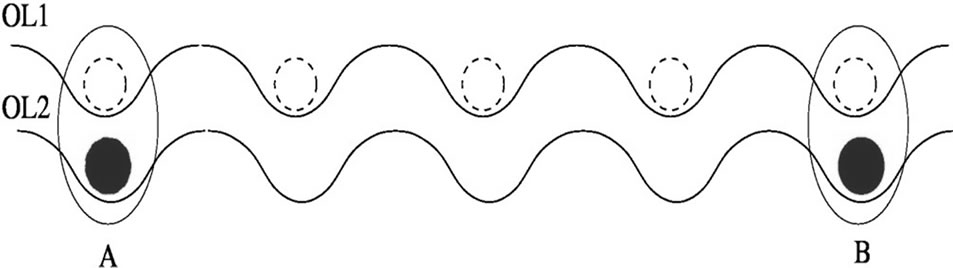
Figure 5. (Color online) Entangling atoms A and B from the spatial modes of the quantum walk with single atom. Optical lattice (OL1) on which quantum walk is implemented is made to overlap with optical lattice on which atoms A and B, to be entangled, are placed (OL2). Radio frequency pulses are used to couple states in the different lattices and entangle A and B.
discussed localization peaks which are symmetric in position space of the walk. As a further extension of the scheme, we can use an arbitrary SU(2) coin operation which can introduce asymmetry in the walk distribution [12], and hence localization can be realized by involving three wave plates, a half-wave plate (H) and two quarter-wave plates (Q) in any of the three configurations Q1Q2H, Q1HQ2 or HQ1Q2 (concatenating the three plates) [40] for each coin operation.
Similarly, delocalized photons after the quantum walk implementation with adjustable coin operations [22] and quantum walk with photons in a waveguide lattice can be directed towards atoms in a spatially separated optical lattice and entangle them.
7. Conclusions
We have presented a scheme for generating entanglement between two distantly located uncorrelated systems using a single particle quantum walk. Spatial modes entangled, due to the interference effect from the quantum walk evolution, were transferred to two distantly located systems and effectively used for the purpose of entangling them. By controlling the amount of entanglement generated between two spatial modes of the quantum walk system we have also shown that the entanglement generated between the two initially uncorrelated systems can be controlled.
The control is brought about by quantum coin operations, localization of the walk evolution at different lattice sites. This scheme to entangle two systems using single particle quantum walk can be directly scaled to simultaneously entangle large systems using many particle walk. We have shown that all the elements of the present scheme are within reach of current experimental setups on which quantum walks have been implemented [14,15, 18-23]. This scheme can come in handy for systems in which only selected sites can be accessed for inducing interaction with uncorrelated systems. Limitations of the resource and the environmental effect are an issue at this point of time, however, experimental progress accounting for decoherence [23] is a positive thrust in the direction of scaling the implementable steps of the walk.
REFERENCES
- R. Horodecki, P. Horodecki, M. Horodecki and K. Horodecki, “Quantum Entanglement,” Reviews of Modern Physics, Vol. 81, No. 2, 2009, pp. 865-942. doi:10.1103/RevModPhys.81.865
- T. Brougham, V. Kostak, I. Jex, E. Andersson and T. Kiss, “Entanglement Preparation Using Symmetric Multiports,” The European Physical Journal D, Vol. 61, No. 1, 2011, pp. 231-236. doi:10.1140/epjd/e2010-10337-2.
- C. Cabrillo, J. I. Cirac, P. Garcia-Fernandez and P. Zoller, “Creation of Entangled States of Distant Atoms by Interference,” Physical Review A, Vol. 59, No. 2, 1999, pp. 1025-1033. doi:10.1103/PhysRevA.59.1025
- M. B. Plenio, S. F. Huelga, A. Beige and P. L. Knight, “Cavity-Loss-Induced Generation of Entangled Atoms,” Physical Review A, Vol. 59, No. 3, 1999, pp. 2468-2475. doi:10.1103/PhysRevA.59.2468
- L. Duan, M. D. Lukin, J. I. Cirac and P. Zoller, “Long- Distance Quantum Communication with Atomic Ensembles and Linear Optics,” Nature (London), Vol. 414, 2001, pp. 413-418. doi:10.1038/35106500
- S. Bose and D. Home, “Generic Entanglement Generation, Quantum Statistics, and Complementarity,” Physical Review Letters, Vol. 88, 2002, Article ID: 050401. doi:10.1103/PhysRevLett.88.050401
- A. K. Ekert, “Quantum Cryptography Based on Bell’s Theorem,” Physical Review Letters, Vol. 67, No. 6, 1991, pp. 661-633. doi:10.1103/PhysRevLett.67.661
- C. H. Bennett, “Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels,” Physical Review Letters, Vol. 70, No. 13, 1993, pp. 1895-1899. doi:10.1103/PhysRevLett.70.1895
- S. J. van Enk, “Single-Particle Entanglement,” Physical Review A, Vol. 72, No. 6, 2005, Article ID: 064306. doi:10.1103/PhysRevA.72.064306
- S. Goyal and C. M. Chandrashekar, “Spatial Entanglement Using a Quantum Walk on a Many-Body System,” Journal of Physics A: Mathematical and Theoretical, Vol. 43, No. 23, 2010, Article ID: 235303. doi:10.1088/1751-8113/43/23/235303
- D. A. Meyer, “From Quantum Cellular Automata to Quantum Lattice Gases,” Journal of Statistical Physics, Vol. 85, No. 5-6, 1996, pp. 551-574. doi:10.1007/BF02199356
- C. M. Chandrashekar, R. Srikanth and R. Laflamme, “Optimizing the Discrete Time Quantum Walk Using a SU(2) Coin,” Physical Review A, Vol. 77, No. 3, 2008, Article ID: 032326. doi:10.1103/PhysRevA.77.032326
- J. Du, H. Li, X. Xu, M. Shi, J. Wu, X. Zhou and R. Han, “Experimental Implementation of the Quantum RandomWalk Algorithm,” Physical Review A, Vol. 67, No. 4, 2003, Article ID: 042316. doi:10.1103/PhysRevA.67.042316
- C. A. Ryan, M. Laforest, J. C. Boileau and R. Laflamme, “Experimental Implementation of a Discrete-Time Quantum Random Walk on an NMR Quantum-Information Processor,” Physical Review A, Vol. 72, No. 6, 2005, Article ID: 062317. doi:10.1103/PhysRevA.72.062317
- D. Lu, J. Zhu, P. Zou, X. Peng, Y. Yu, S. Zhang, Q. Chen and J. Du, “Experimental Implementation of a Quantum Random-Walk Search Algorithm Using Strongly Dipolar Coupled Spins,” Physical Review A, Vol. 81, No. 2, 2010, Article ID: 022308. doi:10.1103/PhysRevA.81.022308
- D. Bouwmeester, I. Marzoli, G. P. Karman, W. Schleich and J. P. Woerdman, “Optical Galton board,” Physical Review A, Vol. 61, No. 1, 1999, Article ID: 013410. doi:10.1103/PhysRevA.61.013410
- B. Do, M. L. Stohler, S. Balasubramanian, D. S. Elliott, C. Eash, E. Fischbach, M. A. Fischbach, A. Mills and B. Zwickl, “Experimental Realization of a Quantum Quincunx by Use of Linear Optical Elements,” Journal of the Optical Society of America B, Vol. 22, No. 2, 2005, pp. 499-504. doi:10.1364/JOSAB.22.000499
- H. B. Perets, Y. Lahini, F. Pozzi, M. Sorel, R. Morandotti and Y. Silberberg, “Realization of Quantum Walks with Negligible Decoherence in Waveguide Lattices,” Physical Review Letters, Vol. 100, No. 17, 2008, Article ID: 170506. doi:10.1103/PhysRevLett.100.170506
- H. Schmitz, R. Matjeschk, Ch. Schneider, J. Glueckert, M. Enderlein, T. Huber and T. Schaetz, “Quantum Walk of a Trapped Ion in Phase Space,” Physical Review Letters, Vol. 103, No. 9, 2009, Article ID: 090504. doi:10.1103/PhysRevLett.103.090504
- F. Zahringer, G. Kirchmair, R. Gerritsma, E. Solano, R. Blatt and C. F. Roos, “Realization of a Quantum Walk with One and Two Trapped Ions,” Physical Review Letters, Vol. 104, No. 10, 2010, Article ID: 100503. doi:10.1103/PhysRevLett.104.100503
- K. Karski, L. Foster, J.-M. Choi, A. Steffen, W. Alt, D. Meschede and A. Widera, “Quantum Walk in Position Space with Single Optically Trapped Atoms,” Science, Vol. 325, No. 5937, 2009, pp. 174-177. http://dx.doi.org/10.1126/science.1174436
- A. Schreiber, K. N. Cassemiro, V. Potocek, A. Gabris, P. Mosley, E. Andersson, I. Jex and Ch. Silberhorn, “Photons Walking the Line: A Quantum Walk with Adjustable Coin Operations,” Physical Review Letters, Vol. 104, No. 5, 2010, Article ID: 050502. doi:10.1103/PhysRevLett.104.050502
- M. A. Broome, A. Fedrizzi, B. P. Lanyon, I. Kassal, A. Aspuru-Guzik and A. G. White, “Discrete Single-Photon Quantum Walks with Tunable Decoherence,” Physical Review Letters, Vol. 104, No. 15, 2010, Article ID: 153602. doi:10.1103/PhysRevLett.104.153602
- W. Dur, R. Raussendorf, V. M. Kendon and H. J. Briegel, “Quantum Walks in Optical Lattices,” Physical Review A, Vol. 66, No. 5, 2002, Article ID: 052319. doi:10.1103/PhysRevA.66.052319
- K. Eckert, J. Mompart, G. Birkl and M. Lewenstein, “Oneand Two-Dimensional Quantum Walks in Arrays of Optical Traps,” Physical Review A, Vol. 72, No. 1, 2005, Article ID: 012327. doi:10.1103/PhysRevA.72.012327
- C. M. Chandrashekar, “Implementing the One-Dimensional Quantum (Hadamard) Walk Using a Bose-Einstein Condensate,” Physical Review A, Vol. 74, No. 3, 2006, Article ID: 032307. doi:10.1103/PhysRevA.74.032307
- Y. Aharonov, L. Davidovich and N. Zagury, “Quantum Random Walks,” Physical Review A, Vol. 48, No. 2, 1993, pp. 1687-1690. doi:10.1103/PhysRevA.48.1687
- A. Ambainis, E. Bach, A. Nayak, A. Vishwanath and J. Watrous, “One Dimensional Quantum Walks with Absorbing Boundaries,” Journal of Computer and System Sciences, Vol. 69, No. 4, 2001, pp. 562-592.
- A. Peres, “Separability Criterion for Density Matrices,” Physical Review Letters, Vol. 77, No. 8, 1996, pp. 1413- 1415. doi:10.1103/PhysRevLett.77.1413
- H. J. Lee, W. Namgung and D. Ahna, “Entanglement Generates Entanglement: Entanglement Transfer by Interaction,” Physical Review A, Vol. 338, No. 3-5, 2005, pp. 192-196. doi:10.1016/j.physleta.2005.03.010
- E. Lieb, T. Schultz and D. Mattis, “Two Soluble Models of an Antiferromagnetic Chain,” Annals of Physics, Vol. 16, No. 3, 1961, pp. 407-466. doi:10.1016/0003-4916(61)90115-4
- M. Christandl, N. Datta, A. Ekert and Andrew J. Landahl, “Perfect State Transfer in Quantum Spin Networks,” Physical Review Letters, Vol. 92, No. 18, 2004, Article ID: 187902. doi:10.1103/PhysRevLett.92.187902
- W. K. Wootters, “Entanglement of Formation of an Arbitrary State of Two Qubits,” Physical Review Letters, Vol. 80, No. 10, 1998, pp. 2245-2248. doi:10.1103/PhysRevLett.80.2245
- T. Oka, N. Konno, R. Arita and H. Aoki, “Breakdown of an Electric-Field Driven System: A Mapping to a Quantum Walk,” Physical Review Letters, Vol. 94, No. 10, 2005, Article ID: 100602. doi:10.1103/PhysRevLett.94.100602
- N. Konno, “Localization of an Inhomogeneous DiscreteTime Quantum Walk on the Line,” Quantum Information Processing, Vol. 9, No. 3, 2010, pp. 405-418. doi:10.1007/s11128-009-0147-4
- C. M. Chandrashekar, “arXiv: 1001.5326,” 2010.
- A. Joye and M. Merkli, “Dynamical Localization of Quantum Walks in Random Environments,” Journal of Statistical Physics, Vol. 140, No. 6, 2010, pp. 1-29. doi:10.1007/s10955-010-0047-0
- C. M. Chandrashekar, “Disordered-Quantum-Walk-Induced Localization of a Bose-Einstein Condensate,” Physical Review A, Vol. 83, No. 2, 2011, Article ID: 022320. doi:10.1103/PhysRevA.83.022320
- K.-A. Brickman Soderberg, N. Gemelke and C. Chin, “Ultracold Molecules: Vehicles to Scalable Quantum Information Processing,” New Journal of Physics, Vol. 11, 2009, Article ID: 055022. doi:10.1088/1367-2630/11/5/055022
- R. Simon and N. Mukunda, “Minimal Three-Component SU(2) Gadget for Polarization Optics,” Physics Letters A, Vol. 143, No. 4-5, 1990, pp. 165-169.
NOTES
*Corresponding author.

