Received 18 March 2016; accepted 22 May 2016; published 25 May 2016

ABSTRACT

This paper presents a dual-band planar antenna array for ISM band applications (2.4 GHz and 2.45 GHz). This antenna is proposed for indoor applications and enables adaptive beamforming and angle of arrival (AOA) estimation. An adaptive beamforming algorithm is applied for a planar antenna array, which is able to steer its main beam and nulls in azimuth and elevation planes over a wide frequency band. Planar antenna array operates as a spatial filter in 3D space, processing the received signals with weighting schemes. A planar antenna array is designed for AOA estimation in azimuth and elevation planes by using MUltiple SIgnal Classification (MUSIC) based on subspace algorithm. The Base Station (BS) equipped with this planar antenna is preferred to be at the center position on the room ceiling to cover all sectors of the room. It is designed to use four directional triangular elements arranged to form a square planar antenna array. Planar antenna with four elliptical slotted triangular elements (PAFESTE) is used to obtain optimal directivity in four directions in azimuth plane with specific orientation of 30˚ in elevation plane. It is characterized by half power beamwidth in elevation plane of about 60˚ and half power beamwidth in azimuth plane of about 90˚.

Keywords:

Indoor Communications, Antenna Array, Directional Planar Antenna, Angle of Arrival Estimation, Adaptive Beamforming

1. Introduction

Smart antenna (SA) is beam-steering antenna which represents an emerging technology to improve the performance of wireless networks [1] . It can form an optimized pattern according to certain rules. It has great advantage in many fields, such as wireless communications systems and radar remote sensing, etc. [2] . Indoor applications are challenged by multipath propagation, and interferences are more likely to occur due to the large number of devices sharing a confined space. The problem is further aggravated by the frequency overlaps between popular standards such as WiFi, Bluetooth and Zigbee. Additionally, many indoor applications are expected to sense the user’s position to implement context-aware services that facilitate access to nearby resources, deliver location sensitive information, and enforce proximity based security policies. To this regard, indoor positioning is actively investigated in recent years, and numerous approaches are proposed in the literature [1] [3] .

Adaptive antenna array is composed of several antenna elements; each element is weighted by pre-defined algorithm. Adaptive antenna array optimizes this algorithm according to user’s requirement, so that the output matches with signals of interest in forming the best antenna pattern. This antenna system is able to detect the existence of the signal source automatically, forms the main beam in the direction of signals of interest, and produces notches in the direction of signals of interference [4] . An antenna array can not only increase the communications range, but also enable the smart antenna technology to be applied to optimize the system performance [5] . Factors affecting performance of adaptive antenna include both the adaptive algorithm and the structure of the antenna array. To arrange the structure (number of elements, distance between feed points, pattern) of antenna array properly can improve the performance of the adaptive array [2] . The smart antenna system estimates the direction of arrival of the signal by using MUSIC algorithm which is subspace based technique. MUSIC algorithm exploits the property that the desired signal array response is orthogonal to the noise subspace. The signal and noise subspaces are identified by using eigen decomposition of the received signal covariance matrix [6] .

This paper presents analysis of 4-antenna elements arranged in a 2 × 2 rectangular planar antenna array. It also studies the impact of the different array elements on the interference signals. Dual-band planar antenna array, namely planar antenna with four elliptical slotted triangular elements (PAFESTE) is proposed to cover the room with frequency and radiation pattern diversity. This prototype is designed to address the challenges of indoor applications. The antenna is intended to augment a wireless devices operating as coordinator or base station (BS). The proposed design is optimized to be installed on the ceiling of any large indoor space. The antenna is implemented by combining four patches pointing to different directions. The radiation pattern direction of PAFESTE is designed to be in direction of 30˚ in elevation plane with a half power beamwidth (HPBW) of 60˚ in elevation plane and HPBW of 90˚ in azimuth plane. Four beams would cover the four sectors of the room. The system can allocate a target by estimating both the azimuth 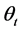and elevation 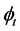angle of arrival (AOA) of the incoming messages [1] .This antenna is designed to operate at frequencies chosen to be inside the 2.4 GHz and 2.45 GHz ISM bands. The design of the proposed PAFESTE antenna is simpler than the design of the proposed configurations in [1] [7] according to two factors. The first factor is that the presented smart antenna is based on 2D planar antenna instead of 3D arrangement as discussed in [1] . The second factor is that it has minimum number of elements with high coverage area to avoid unnecessarily high complexity in the signal processing unit with a significant cost savings. The design of the proposed wireless sensor antennas is numerically analyzed by using the finite element method (FEM) [8] . An adaptive beamforming algorithm is applied for a PAFESTE, which is able to steer its main beam and nulls in azimuth and elevation planes. A PAFESTE is designed for AOA estimation in azimuth and elevation planes using the MUSIC based on subspace algorithm.

2. Antenna Array Design

A planar antenna array with four elliptical slotted triangular elements (PAFESTE) is proposed as a simple configuration with a minimum number of elements to cover all sectors inside a room. The proposed square planar antenna array consists of identical isosceles four triangular elements of identical characteristics. These elements are printed on the top of a square grounded dielectric slab. The HFSS model of PAFESTE with inner and outer dimensions is shown in Figure 1. An elliptical slot is serving as a perturbation shape and it is used to increase the path length of the surface current. This antenna is designed on the FR-4 epoxy PCB substrate with a thickness of 1.6 mm, a dielectric constant of 4.4, and a dielectric loss tangent of 0.02 [7] . PAFESTE is designed to operate in frequency range from 2.4 GHz to 2.45 GHz. The calculated reflection coefficient of the designed PAFESTE is shown in Figure 2.

Each isosceles triangular patch antenna exhibits a radiation pattern with a peak at 30˚ in elevation plane and a maximum gain of 0.2166 dBi at 2.4 GHz. The peak of the radiation pattern is at 10˚ in elevation plane and the maximum gain is −0.0613 dBi at 2.45 GHz as shown in Figure 3.

At 2.4 GHz the proposed antenna is characterized by half power beamwidth in elevation plane of about 60˚ and half power beamwidth in azimuth plane of about 90˚ as shown in Figure 4. The radiation patterns of PAFESTE in four directions of azimuth plane are shown in Figure 5.

3. Planar Antenna Array

Linear arrays lack the ability to scan in 3-D space. However it is necessary for portable devices to scan the main beam in any direction of 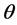(elevation) and 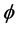(azimuth), planar arrays are more attractive for these mobile devices. Figure 6 shows the elements of the reception part of a smart antenna. The antenna array contains four elements. The four signals are being combined into one signal, which is the input to the receiver. The proposed example can be considered as a rectangular planar array, which is used to increase gain and enable beam steering. The array has a relatively low number of elements in order to avoid unnecessarily high complexity in the

signal processing. This structure can perform beamforming in azimuth and elevation angles in 3-D space.

The planar array PAFESTE is considered as a rectangular planar antenna array in the x-y plane. It can be viewed as M linear arrays of N elements or as N linear arrays of M elements creating array of elements. The x-directed elements are spaced dx apart and the y-directed elements are spaced dy apart. By taking into account the gain of each m − nth element, the array factor in [9] is

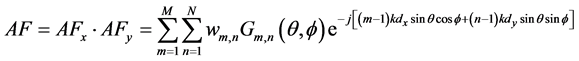(1)

where 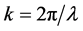is the propagation constant in free space and 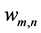is the complex weight of each element.

The analysis in [10] is extended to two dimensional planar array, where the array as shown in Figure 6 has a reference element (element 1,1) at the origin and the coordinates of the m − nth antenna element are marked as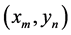. The signal as it travels across the array undergoes a phase shift. Consider a transmitted signal in complex envelope representation:

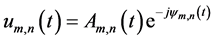(2)

where is the magnitude and is the phase of the signal. The main beam of PAFESTE is steered in different directions in azimuth and elevation planes. If a single plane wave is incident on the antenna array, then

. (3)

A complex quantity is defined as the ratio between the signal received at the m − nth antenna element and the signal received at the reference element when a plane wave is incident on the array. For adaptive beamforming, each array element output is multiplied by a complex weight modifying the phase and amplitude relation between the branches, and summed to give

(4)

where W is the weight vector, T denotes transpose matrix operation and is the array response vector (ARV). The response of the array with the weighting network is called the array factor and it’s defined as:

(5)

4. Adaptive Beamforming

In an adaptive array, the weights are adapted by minimizing certain criterion to maximize the signal-to-interfe- rence plus noise ratio (SINR) at the array output [11] .

4.1. Beamsteering in 2D Space

The analysis of adaptive beamforming in [12] is extended to two dimensional planar array by taking into account the gain of each element. Assume the desired source and interfering sources transmit signals with the same carrier frequency impinge on the element URA (Uniform Rectangular Array) and arrive at, which is the maximum directivity in elevation plane. The proposed PAFESTE is element URA, where the distance between each two feed points of the adjacent elements is. The useful signal arrives from angle and the interfering signals arrive from angles.

For adaptive beamforming, each element output of the element URA is multiplied by a complex weight. So the complex sensor weights are, , ,

. Therefore, the array output due to is given by

(6)

and due to the ith interfering signal is given by

. (7)

where is the phase shift between the m − nth element and the reference element due to and

is the phase shift between the m − nth element and the reference element due to the ith interfering signal.

The total array output is given by:

. (8)

There are eight unknowns to be determined, the four real parts and the four imaginary parts of the four complex weights such that the element URA to recover the desired signal and fully cancel out the three interfering signals. Equivalently, the total array output must be equal to the useful signal, or

. (9)

For convenience, we define the dimensional vector W as

(10)

where both and are 4 dimensional vectors consisting of the real and imaginary parts of the complex weights of the array elements, respectively.

Furthermore, the four matrices, , , and, all depend on and. After getting these matrices, the total array output is obtained by:

. (11)

From Equation (11), solution to Equation (9) is given by

(12)

The dimensional vector Q can be written as

(13)

where both and are 4 dimensional vectors. is interpreted as preserving the real part of the useful signal and cancelling out the real parts of all the interfering signals. Similarly, is interpreted as nulling out imaginary parts of the useful signal and all the interfering signals.

The proposed antenna array has a half power beamwidth for each element in azimuth plane as shown in Figure 5. So is given by

. (14)

The gain of each element is modeled using the following parametric function [13] :

(15)

where is the gain at, , and m corresponds to the directivity. The radiation pattern for a weighted element URA in dB is given by

. (16)

T the incoming signal of interest arrives is assumed to be at angle and three interfering signals from angles, ,. Figure 7 represents an example of a beam forming for the element URA with directional pattern of for each element.

4.2. Beamsteering in 3D Space

If the element URA is beam steered toward the angles and nulled the three interfering signals from angles, ,. The 3D ra- diation pattern for a weighted element URA in dB is given by

. (17)

Figure 8 represents a top view of the 3D radiation pattern for a weighted element URA with directional pattern for each element of in elevation plane. Figure 9 represents a top view of the 3D radiation pattern for a weighted element URA with directional pattern for each element of in elevation plane, where and.

5. Angle of Arrival Estimation

The AOA estimation algorithms are directly associated with the received signals. Data from an array of sensors are collected, and the objective is to locate point sources assumed to be radiating energy that is detectable by the sensors. Mathematically, such problems are modelled using MUSIC (MUltiple SIgnal Classification), which is a high resolution direction finding (DF) algorithm [14] . It has been presented in the context of estimating the angle of arrival of the received signal in azimuth and elevation planes. For the intended application, a few reasonable assumptions can be invoked to make the problem analytically tractable. The transmission medium is assumed to be isotropic and nondispersive and the sources are located in the far-field of the array, so that the radiation impinging on the array is in the form of sum of plane waves. The analysis of AOA estimation in [12] is extended to two dimensional planar array by taking into account the gain of each element.

5.1. Array Response Vector

An antenna array is composed of identical elements with directional radiation pattern; each element receives a time-delayed version of the same plane wave with wavelength. Each element receives a phase-shifted version of the signal. The array response vector (ARV) is the response of an array to an incident plane wave. It is a combination of the steering vector and the response of each individual element to the incident wave. The general ARV expression for a two-dimensional array of elements is.

5.2. Received Signal Model

For the case where V uncorrelated sources transmit signals to element antenna array. The array response for each signal is a function of. The received signals can be expressed as a superposition of signals from all the sources and linearly added noise represented by:

(18)

where is the complex baseband equivalent received signal vector at the antenna array at time (t) and is the incoming plane wave from the vth source at time t and arriving from the direction, is the array response vector to this direction, and represents additive noise. A single observation from the array is often referred to as a snapshot. In matrix notation, Equation (18) can be written as

. (19)

The array response matrix is parameterized by AOA, where the maximum number of uncorrelated sources is two sources in the proposed example. is the vector of all the AOAs and represents the vector of the incoming signal in amplitude and phase from each signal source at time t.

For a set of data observations L:

(20)

where X and and, so.

5.3. The MUSIC Algorithm

The incident signals are assumed to be sinusoidal baseband frequency modulated signals of uncorrelated sources with different phase shift impinge on the proposed elements URA. In the present case, two equal- power sources are located in the far-field of the array, with and

. Moreover, uncorrelated spatially white Gaussian noise with zero mean and unit variance is assumed. A total of 500 observations are taken (). The average over a finite, sufficiently enough, number of data “snapshots” is used in practical implementations. The received signal autocovariance matrix is given by

(21)

where H denotes Hermitian (or complex-conjugate transpose) matrix operation. The signal subspace and the noise subspace are gotten by eigendecomposition of the autocovariance matrix of the received data. The MUSIC spatial spectrum equation in [12] is modified to be applied in azimuth and elevation planes and is function of each element gain. Then, the AOAs of the desired signals can be estimated by calculating the MUSIC spatial spectrum over the region of interest.

. (22)

Figure 10 shows the top view of MUSIC spatial spectrum results in dB for a (2 × 2) element URA with directional pattern of half power beamwidth 60˚ for each element, where it is obtained in azimuth and elevation plane. The performance of the MUSIC algorithm in azimuth and elevation planes is shown to be excellent as the one plane example in [12] , where the peaks in the spatial spectrum are located at angles being exactly the AOAs.

6. Conclusion

A new smart antenna “PAFESTE” is introduced to be used in wireless applications in the frequency range from 2.4 GHz to 2.45 GHz bands. The PAFESTE is a planar antenna array, which is designed to be applicable for indoor applications. The proposed antenna is simulated by using HFSS. An adaptive beamforming algorithm is applied for the proposed planar antenna array, which is able to steer its main beam and nulls in azimuth and elevation planes. The subspace based technique, MUSIC algorithm is used to estimate the direction of arrival of the signal that impinges on the PAFESTE. The adaptive beamforming algorithm exhibits a good accuracy and precision results in azimuth and elevation planes, where the shift between the peak of the desired signal and the interferers is about 15 dB for the HPBW of 90˚ and 10 dB for the HPBW of 60˚, so there are no dead points and the planar antenna array operates as a spatial filter in 3D space.

Cite this paper

R. Elsamnty,A. M. Attiya,E. A. F. Abdallah,A. H. Ammar, (2016) Beamforming and Angle-of-Arrival Estimation of Square Planar Antenna Array. Open Journal of Antennas and Propagation,04,13-23. doi: 10.4236/ojapr.2016.42002

References