Received 6 October 2015; accepted 25 December 2015; published 28 December 2015

ABSTRACT

In microwave tomography, it is necessary to increase the amount of diverse observation data for accurate image reconstruction of the dielectric properties of the imaging area. The multi-polari- zation method has been proposed as a suitable technique for the acquisition of a variety of observation data. While the effectiveness of employing multi-polarization to reconstruct images has been confirmed, the physical considerations related to image reconstruction have not been investigated. In this paper, a compact-sized imaging sensor using multi-polarization for breast cancer detection is presented. An analysis of the correlation coefficient of the received data of adjacent antennas was performed to interpret the imaging results. Numerical simulation results demonstrated that multi-polarization can reconstruct images better compared to single polarizations owing to its low correlation coefficient and condition number.

Keywords:

Microwave Tomography, Inverse Scattering, Distorted Born Iterative Method (DBIM), Breast Tumor, Correlation Coefficient

1. Introduction

In Japan, the breast cancer incidence and associated mortality rates of women are lower compared to Western countries. However, it is one of the major causes of death among women, and the incidence rate has increased since 1975, regardless of age group [1] . Therefore, early detection of breast cancer is important because it helps prevent and reduce deaths from breast cancer. In Japan, breast cancer screening by X-ray mammography is recommended for women aged over 40. However, X-ray mammography involves risks, such as X-ray exposure, overlooked tumors owing to the low contrast of breast tissue, and pain during the examination. In addition, a combination of palpation and ultrasound diagnosis is also commonly used in breast cancer screening. Because the examination results depend on the skill of the examiner, the probability of cancer detection can differ accordingly. For the above reasons, an alternative to current breast cancer screening methods is required.

Recently, studies on the early detection of breast cancer by microwave imaging (MWI) have attracted considerable interest among researchers [2] . This approach to breast cancer detection uses a fundamental principle? when electromagnetic waves are irradiated to the imaging region, scattered waves are generated by the differences in the dielectric properties of the cancer and the normal breast tissue [3] . The MWI method can be classified to ultra-wideband (UWB) radar and tomography. In our laboratory, we have developed a multi-static UWB radar measurement system for the early detection of breast cancer and conducted clinical trials. The results demonstrated that the system can detect cancer that has a clear boundary and is isolated from fibro-glandular tissue. However, if the boundary of the fibro-glandular tissue and the cancer is irregular, the system was unable in some cases to correctly reconstruct the shape of the cancer [4] -[6] . Thus, the proposed diagnostic method using UWB radar can be considered incomplete. Therefore, we are currently working on the development of a microwave tomography method for early breast cancer screening by reconstructing the dielectric property distributions of the examined breast [7] -[9] .

In microwave tomography, the electromagnetic waves are efficiently incident on the object. The influence of surrounding structures is avoided by immersing the antenna and imaged object into a lossy matching fluid [10] . In order to achieve accurate image reconstruction, it is necessary to obtain diverse observations data. Several methods must be considered. The amount of observation data can be increased by increasing the number of antennas; however, the antennas must be arranged at a certain distance from each other. Thus, the scale of the apparatus increases and the computational cost becomes substantial. Furthermore, the signal-noise ratio (SNR) is degraded by this method, which creates difficulties in the correct reconstruction of the image. A method using multiple frequencies has been proposed [11] . In general, biological tissue is a medium with frequency dependence, and its behavior is modeled using the Debye approximation with several parameters. In this method, the number of unknown parameters is increased along with the number of frequencies; thus, the reconstruction becomes difficult and the images are reproduced with low accuracy.

Furthermore, the multiple-polarization method has been examined as a means to obtain a variety of observations data. The changes in the polarization of the scattered waves are influenced by the composition and shape of the biological tissue. For example, a dual-polarized MWI system that can simultaneously collect both TE and TM polarizations using scattering probes has been built to obtain 2-D tomographic images [12] . The polarized data are inverted using contrast source inversion (CSI) algorithm to reconstruct the electrical properties. However, there are some issues regarding the imaging quality of the system. In [13] , the impact of polarization on image reconstruction was evaluated with a shielded array of patch antennas using truncated singular-value decomposition (TSVD) analysis. The multi-polarization layout was observed to enhance the imaging performance with a higher truncation index compared to uniform array configurations. Although the effectiveness of employing multi-polarization to reconstruct images have been established, to our knowledge, the physical considerations related to antenna arrangement in order to achieve sufficient image reconstruction have not yet been investigated. This information can be used as a viable parameter in sensor design.

In this paper, we present a compact-sized imaging sensor using the multi-polarization method for breast cancer detection. Based on our previous paper [7] , we confirmed the image reconstruction by solving the inverse problem using the Newton-Kantorovich method, as explained in [14] . Because of the extensive calculations of the inverse matrix performed to compute the Jacobian, this method involves problems, such as low resolution and high computational cost. Therefore, we employ the Distorted Born Iterative Method (DBIM), described in [15] [16] , which does not require inverse matrix calculation for the computation of the Jacobian. We use a different antenna arrangement from [7] [9] to show the impact of polarizations on 3-D image reconstruction at various antenna locations. We also clarify the impact on physical measurements using the analysis of the correlation coefficient of the received data from adjacent antennas.

This paper is organized as follows. The imaging algorithm approach employed for image reconstruction is described in Section 2. Section 3 presents our proposed compact-sized imaging sensor and breast model used for numerical simulation. Further in Section 3, the imaging results are presented and discussed. Finally, Section 4 discusses the conclusion of our paper.

2. Imaging Algorithm

In tomography, the breast model is expressed as a cube and discretized as voxels, and the dielectric properties are estimated in each voxel. The total number of voxels is K, and the dielectric properties, which consist of the relative permittivity and conductivity distribution, are represented by contrast. The calculated data group, , which is based on the estimated model is compared with the measured data group, 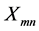, which is based on the actual model (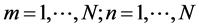, where N is the total number of antennas, m is the number of transmitters, and n is the number of receivers). The contrast distribution of the breast model is iteratively updated by the DBIM until 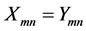is reached. The image reconstruction is accomplished by minimizing the norm of the difference between measured and calculated scattering data.

2.1. Inverse Scattering Problem and DBIM

The governing equation for the scattering field at an observation point r for a given frequency is

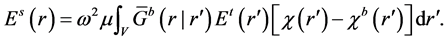(1)

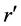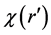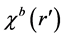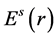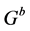Here, is an arbitrarily position vector in the imaging region , is the unknown contrast, is the contrast of the background, is the scattered electric field at the observation points, is the total field, is the dyadic Green’s function, ω is the angular frequency, and μ is the magnetic permeability.

Equation (1) is a nonlinear integral equation; therefore, we employ the DBIM to solve the nonlinear problem. DBIM is equivalent to the Gauss-Newton method that is used in nonlinear least-squares optimization problems to obtain an approximate solution for the contrast. In the iterative DBIM, we start with an initial guess of the contrast in the imaging region. At each iteration, we determine the contrast perturbations based on the approximate solution of the inverse problem, and then update the contrast. The updated contrastis referred to as the new contrast of the background; the total field and the scattering field at the observation points are recalculated based on the new contrast. Then, the calculated scattering field is compared with the measured scattering field to minimize the residue error until convergence is reached.

2.2. Linearization of the Scattering Equation

In this paper, the contrast function, 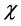is represented by Equation (2), where 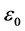is the vacuum permittivity, is the relative permittivity of the background, 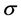and are the conductivity and relative permittivity of the imaging object, respectively. The conductivity, and relative permittivity, are the unknown parameters that will be measured.

(2)

As we mentioned earlier, Equation (1) is a nonlinear equation. In order to linearize Equation (1) in the Born approximation, the incident field is adopted instead of total field. In this paper, we use the recalculated total field obtained at each iteration with respect to the unknown contrast function to linearize the nonlinear equation. Equation (2) is applied to Equation (1) and is discretized, thus resulting in a linear relationship between the scattered field and the contrast function. Because the two unknown parameters in the contrast function are real numbers, the equation is divided into a real and an imaginary part to form linear equations of a real numbers, as expressed by Equation (3).

(3)

is the difference between the measured scattered field, which is based on the actual model, and the calculated scattered field, which is based on the current contrast distribution. and denote the real and imaginary parts of the complex number, respectively. From Equation (3), a linear equation of the form is obtained. Here, vector is the perturbation used to update the contrast; meanwhile, the residual scattering field between the measured data and the calculated data from the current contrast at the observation points is placed in vector. Furthermore, the sensitivity matrix, known as the Jacobian, that shows the changes in the calculated data at the current contrast distribution is equivalent to matrix. For a system with K unknowns and measurements, the unknown contrast is, the residual scattered field is, and the Jacobian matrix is configured as.

In the linear model of Equation (3), an approximation of the contrast perturbations, is determined by Equation (4).

(4)

Here, k is the iteration number, and + denotes the conjugate transpose of a matrix. Because the inversion in Equation (4) is ill-posed, conjugate gradient (CG) regularization is applied at each iteration to estimate the contrast perturbations and to update and generate a new contrast. Then, the imaging region is reconstructed using the new contrast, and this process is repeated until the residual norm is smaller.

3. Numerical Simulation

In the inverse scattering problem, a large amount of diverse observation data is required to achieve accurate image reconstruction with high resolution. In addition, the measurement error increases if the SNR decreases; thus, it cannot reconstruct the image accurately. Therefore, it is necessary to minimize the analysis region in order to reduce the computational cost. For this reason, the implementation of a compact sensor that involves a small distance between the antenna and the breast is preferred. In this case, large number of antennas must be arranged in a small and limited space. Various observation data can be obtained even in a small space by changing the plane of polarization.

3.1. Imaging Sensor and Breast Model

Figure 1 shows the imaging sensor with dimensions 48 × 96 × 48 mm (width × length × height). The imaging region is discretized into 8-mm resolution. For simplicity, a point source is used for the antennas, and arranged in a 4 × 2 configuration on each of the four side-panels of the sensor. Figure 1(a) shows the position of the antenna. One of the antennas is used for transmitting, and all the elements including transmitter are used for receiving data. The lines in Figure 1 represent the polarization direction of the antenna, where the y-axis indicates vertical polarization, and the x- or z-axis horizontal polarization. The antenna arrangements for each side are identical, and the four side-panels are parallel to either the xy- or zy-plane. In this paper, we investigated three different configurations, as shown in Figure 1, to examine the effectiveness of polarization in breast cancer detection. Figure 1(a) illustrates the vertical polarization, Figure 1(b) the horizontal polarization, and Figure 1(c) vertical and horizontal polarization (hereafter referred to as multi-pola- rization). Here, we did not arrange antennas on the top surface of the panel to clearly show the effect of polarization.

We assumed that the imaging sensor is constructed from resin, which has properties similar to those of adipose (fatty) tissue. A hemispheric volume is providedinside the sensor to accommodate the breast model,

similar to the imaging sensor with fixed suction proposed in [4] . The simple breast model shown in Figure 2 consists of adipose tissues, fibro-glandular tissues, and a tumor. The breast model is a hemisphere with a radius of 48 mm, and the tumor has a radius of 4 mm. The analysis region is limited to the hemispheric space containing the breast model; the chest wall under the breast was also modeled. The analysis region is discretized into 8-mm voxels, thus it composed of 538 voxels. We characterized the dielectric properties of the breast model in each voxel, as shown in Table 1.

3.2. Numerical Results and Discussion

The total field within the scattering object was calculated according to the method of moment (MOM), as described in [14] . In previous research investigating MWI for biomedical applications, operating frequencies of 1.0 - 2.3 GHz [17] and 2.45 GHz [18] were used. Here, we used a single frequency of 2.5 GHz.

3.2.1. Image Reconstruction of Breast Models

In Model 1, the analysis region consists of the chest wall, adipose tissue, and a tumor. The distributions of the two unknown parameters, i.e., the relative permittivity and conductivity, are shown in Figure 3. The parameter-setting model of Model 1 is shown in Figure 3(a), where the chest wall has been omitted. Figures 3(b)-(d)

show the results of the 3-D image reconstruction after 100 iterations, using vertical, horizontal, and multi-pola- rization, respectively, for transmitting and receiving data. From the results, we cannot estimate both the relative permittivity and the conductivity of the tumor using single polarizations, i.e., vertical and horizontal polarization. In contrast, Figure 3(d) clearly indicates the presence of the tumor and the reconstruction is successfully for both parameters using multi-polarization.

Figures 4(a)-(b) show the setting and reconstruction value of the relative permittivity and conductivity through the tumor voxel. The x-axis indicates the x-coordinate of the voxel, and the y-axis indicates either the relative permittivity or conductivity. The setting values of the relative permittivity and conductivity of the voxel corresponding to the tumor are 52 and 4 [S/m], respectively. The reconstructed parameters of the tumor for the different polarizations are summarized in Table 2. We observed that the dielectric properties of the tumor are lower than the expected setting values when using single polarizations. However, the dielectric properties of the tumor are improved and accurately estimated using multi-polarization.

For Model 2, the analysis region consists of the chest wall, adipose tissue, fibro-glandular tissue, and a tumor. Here, 10% of the volume ratio of the breast is occupied by fibro-glandular tissues that are distributed randomly. Figure 5(a) is the setting model of Model 2 and the tumor is marked by an arrow for clarity. Figures 5(b)-(d)

^aVertical polarization. ^bHorizontal polarization. ^cMulti-polarization.

show the results of the 3-D reconstructed images after 230 iterations, using vertical, horizontal, and multi- polarization, respectively. As shown in Figure 5(b), the reconstruction of the tumor cannot be performed correctly when vertical polarization antennas are used. Moreover, the image reconstruction is insufficient when using horizontal polarization. However, the results in Figure 5(d) indicate that the image reconstruction of the breast is accurate when using multi-polarization antennas for transmitting and receiving.

Figures 6(a)-(b) show the setting and reconstruction values of the dielectric properties of the tumor voxel in the x-axis direction. Figure 6(a) demonstrates that the relative permittivity of the tumor is relatively high when using horizontal polarization and low when using vertical polarization. Nevertheless, the reconstruction value obtained using multi-polarization is similar to the setting value. In addition, the conductivity of the tumor is improved and accurately estimated when using multi-polarization. Table 2 shows the reconstructed relative permittivity and conductivity values of the tumor when using different polarizations in Model 2.

In Model 2, the tumor is adjacent to fibro-glandular tissues and the contrast difference between them is small. The above findings confirm that we can detect the tumor accurately with the presence of fibro-glandular tissues by employing multi-polarization. Overall, the results from both breast models indicate that vertical and horizontal polarization provide different information of the image reconstruction and dielectric properties. The multi- polarization array configuration consistently performed better than single polarizations.

3.2.2. Correlation Coefficient of Adjacent Antennas

In this section, we investigated the impact on image reconstruction by the analysis of the correlation coefficient of the received data between adjacent antennas in our imaging sensor. First, we examined the positions of the antennas shown in Figure 1(a), with the upper antenna at 24 mm and the lower antenna at 8 mm (Position 1). Table 3 summarizes the correlation coefficients for different polarizations. At this position and for Model 1, we observed that single polarizations achieve correlation coefficients close to 1 and the correlation coefficient of the multi-polarization result is 0.1555, relatively low compared with the single polarizations. Model 2 also shows a similar tendency. Next, we changed the position of the upper antenna to 32 mm (Position 2), and finally the position of the lower antenna to 16 mm (Position 3). The results for the two new positionsare tabulated in Table 3. We observed that the results show a similar trend to that exhibited at Position 1 for both breast models.

Overall, the correlation coefficient of the receiver pair was significantly reduced when using multi-polariza- tion compared to single polarizations. At Position 1, adequate image reconstruction was obtained using multi- polarization owing to the low correlation coefficient, as shown in Figures 3-6. Furthermore, the correlation coefficient of the multi-polarization results at Position 3 is higher than that at Position 1 for both models. Figures 7(a)-(c) show the x-axis projection of the setting and reconstruction values of the dielectric properties of the tumor voxel for Model 1 obtained using multi-polarization. These results demonstrate that positions with low correlation coefficients reconstruct the dielectric properties sufficiently. Therefore, we can conclude that a low correlation coefficient is a viable condition for successful image reconstruction.

3.2.3. Condition Number of the Inverse Matrix

The condition number of a matrix characterizes the solution sensitivity of a linear equation system to errors in the data and it indicates the accuracy of the results from of the matrix inversion. We examined the condition number of the inverse matrix for the two breast models using different polarizations; these are summarized in Table 4. For Model 2, when horizontal polarization is used, the condition number is slightly decreased from 12.07 to 11.76 at the second iteration. Then, the condition number exhibits unstable changes with increasing iteration number and obtains a significantly high value of 3.08 × 10³ at the 230^th iteration. This suggests that the

reconstruction of the dielectric property distributions may not be performed correctly owing to the ill-posed problem of the inverse matrix. In contrast, when vertical polarization is used, the condition number decreases to 11.78 at the second iteration. Subsequently, it increases with increasing iteration number. Although an increase occurred in the condition number, it was small compared to that observed for the horizontal polarizations.

Lastly, when multi-polarization is applied to the imaging sensor, the condition number slightly increases to 12.16 at the second iteration. Subsequently, the condition number varies moderately with the iteration number and reaches 13.80 at the 230^th iteration. Model 1 showed a similar tendency. From these results, we conclude that the ill-posed problem does not occur when multi-polarization is applied. Thus, the images and dielectric properties of the breast can be reconstructed. Figure 8 shows the changes in the condition number as a function of iteration number for Model 1. The figure demonstrates that multi-polarization is an effective method for image reconstruction nowing to the small and smooth variations in the condition number.

4. Conclusion

We have confirmed the effectiveness of applying multi-polarization to transmit and receive antennas to determine the dielectric property distributions of a simple breast model. For the imaging algorithm, this is accomplished using the MOM and DBIM in the inverse scattering problem. The numerical simulation results demonstrated that the ill-posed problem can be avoided because of the improvement of the condition number by multi-polarization. Furthermore, the correlation coefficient of multi-polarization is relatively low compared to those

corresponding to single polarizations. For this reason, the correlation coefficient may represent a viable parameter for image reconstruction in microwave tomography aimed at breast cancer detection.

Cite this paper

L.Mohamed,N.Ozawa,Y.Ono,T.Kamiya,Y.Kuwahara, (2015) Study of Correlation Coefficient for Breast Tumor Detection in Microwave Tomography. Open Journal of Antennas and Propagation,03,27-36. doi: 10.4236/ojapr.2015.34004

References

NOTES

^*Corresponding author.